文章编号:1004-0609(2008)S1-0219-04
多相平衡计算的元素势法及其应用
汪金良1, 2,童长仁2,张传福1,张文海1,3
(1. 中南大学 冶金科学与工程学院,长沙 410083;
]2. 江西理工大学 材料与化学工程学院,赣州 341000;
3. 中国瑞林工程技术有限公司,南昌 330002)
摘 要:针对冶金化工领域中多相反应体系的高效可靠计算问题,基于最小吉布斯函数原理和质量守恒定律,通过引入拉格朗日因子λe,运用元素势概念,推导基于元素势的多相平衡计算方法。结果表明:酯化反应多相复杂体系平衡计算结果与文献值吻合很好,铜造锍熔炼过程多相平衡计算结果与生产实践数据之间的误差小于6%;该方法具有求解速度快,且在计算过程中不会出现负摩尔分数,说明此研究方法对求解复杂冶金化工多相平衡问题是有效可行的。
关键词:元素势;化学反应;相平衡
中图分类号:TQ 02;TF 801.2 文献标识码:A
Element potential method and its application for multi-phase equilibrium calculation
WANG Jin-liang1, 2, TONG Chang-ren2, ZHANG Chuan-fu1, ZHANG Wen-hai1, 3
(1. School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China;
2. Faculty of Materials and Chemical Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;
3. China Nerin Engineering Co., Ltd, Nanchang 330002, China )
Abstract: For the efficient and reliable calculation of multi-phase reaction system in metallurgical and chemical fields, the element potential method for multi-phase equilibrium calculation was deducted based on the least Gibbs function principle and the conservation of mass, by introducing Lagrange factor λe and the concept of element potential. The calculation results show that the calculation values of esterification multi-phase equilibrium system are in good agreement with the reported values, and the errors are less than 6% between practical data and calculation values in the copper smelting process. The calculation speed of this method is fast, and there is no negative mole fraction in the calculation process. It’s proved that this method is feasible and effective to solve the complex metallurgical chemical multi-phase equilibrium problem.
Key words: element potential; chemical reaction; phase equilibrium
在冶金、化工生产实践中,多相反应平衡计算具有广泛的应用基础[1-2]。目前,多相平衡计算的主流算法有化学平衡常数法和最小吉布斯函数法两类。前者的主要缺点是需给出独立反应方程,通用性差,方程多,计算量大;后者有RAND法[3-4]、NASA法[5]、Wolfe法[6]等,该类方法具有无需确定体系化学反应方程、通用性强等优点,但对于含有微量组分的体系,在程序实现中,要采取必要的措施,防止迭代求解过程中出现负数。
元素势的概念由POWELL[7]和REYNOLDS等[8]提出,过道明等[9]对元素势的理论基础及其物理意义进行了阐述,并举例说明了应用元素势法进行系统平衡分析的过程。
本文作者基于最小吉布斯函数原理,结合质量守恒定律,通过引入拉格朗日因子λe,运用元素势概念,推导基于元素势的多相平衡计算方法。该方法具有求解变量少、计算速度快、精度高,且在计算过程中不会出现负摩尔分数等特点,为复杂冶金化工过程多相热力学平衡的高效可靠求解问题提供了一种有效方法。
1 元素势
设多相体系的总相数为P,各相用p表示,p=1,2,…,P,第p相中含有Cp个组分,以pc表示第p相中的第c个组分,c=1,2,…,Cp。在恒温恒压条件下,体系总的吉布斯函数可用式(1)表示:

由最小吉布斯函数原理可知,当体系处于平衡状态时,体系总的吉布斯函数最小,结合质量守恒约束条件式(2),多相平衡求解问题可归结为有约束条件的极值求解问题。

按拉格朗日因子法,构造L函数式(3),将有约束条件的极值问题转化为无约束条件的极值问题。
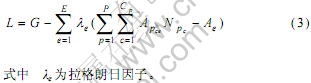
对式(3)求偏导:
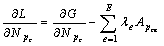 (4)
(4)
因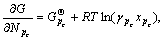 代入式(4)得:
代入式(4)得:
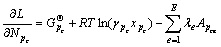 (5)
(5)
系统处于平衡状态时,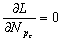 ,所以由式(5)得:
,所以由式(5)得:
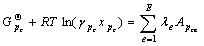 (6)
(6)
将式(6)每摩尔pc组分的吉布斯函数,通过拉格朗日因子λe,与构成pc组分的各种元素的原子数量联系起来,由于其值等于所含各种原子的数量与对应的拉格朗日因子λe乘积之和,因此,λe称为e元素的元素势。由于pc是系统中的任一组分,所以在平衡系统中,同种类原子的元素势与其存在形态无关,即无论同种类原子处于系统的哪一相哪一种分子中,其元素势值均相同,但元素势与系统有关。
2 基于元素势的多相平衡求解算法
由式(6)有:
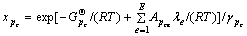 (7)
(7)
由摩尔分数的定义有:
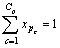 (p=1,2,…,P) (8)
(p=1,2,…,P) (8)
将式(7)代入式(8)得:
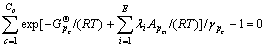 (p=1,2,…,P) (9)
(p=1,2,…,P) (9)
定义Np为第p相中各组分摩尔数之和,则有
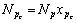 ,这样由式(2)和式(7)有:
,这样由式(2)和式(7)有:
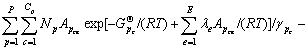 Ae=0 (e=1,2,…,E) (10)
Ae=0 (e=1,2,…,E) (10)
联立方程(9)和(10),即为元素势法多相平衡方程组。
从方程(9)和(10)可以看出,元素势法多相平衡方程组共有P+E个方程,或者说仅有P+E个待求变量,而平衡常数法有P+∑Cp (各相平衡产物数之和)个方程,基于最小吉布斯函数的RAND算法有E+∑Cp个。实际上,在绝大多数多相平衡计算中,P?∑Cp,E?∑Cp,因此,基于元素法的多相平衡求解算法在速度上具有明显优势。从式(7)可知,采用元素势法求解不可能得出负的摩尔分数,因而特别适用于含有微量平衡组分的多相平衡计算。由于元素法本质上基于最小吉布斯原理,所以保留了不需要确定独立化学反应的优点。
方程(9)和(10)可用最速下降法或Newton-Raphson法求解。
3 计算举例
3.1 酯化反应
体系有4 个组分:乙醇(EtOH)、乙酸(HAc)、乙酸乙酯(EtAc)、水(H2O)。进料组成为0.5 mol EtOH,0.5 mol HAc。反应压力为105 Pa,温度为355 K。假设气相为理想气体,液相模型用NRTL方程计算(活度系数模型参数取自文献[10]),该体系气液两相平衡计算结果如表1所列。
表1 酯化反应平衡计算结果
Table 1 Result of esterification balance
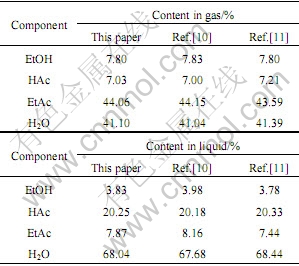
由表1可以看出,本研究得到的平衡组成同文献[10-11]的结果吻合很好,并且平衡时的吉布斯自由能函数值更小。
3.2 铜造锍熔炼过程
铜造锍熔炼过程可视为铜锍、炉渣和烟气三相平衡体系[12],其中铜锍相包含Cu2S、FeS、FeO、Fe3O4等组分,炉渣相包含FeO、SiO2、Cu2S、Cu2O、Fe3O4、FeS等组分,烟气相包含SO2、S2、O2、N2、H2O、H2、CO、CO2等组分。计算采用某厂某时期稳定生产的平均数据,即温度1 493 K,混合精矿处理量168 t/h,熔剂率10%;混合精矿主要成份为:Cu 26.65%,S 30.44%,Fe 26.98%,SiO2 5.73%,其它10.20%;送风量及风含氧量为:工艺风 34 481 Nm3/h,工艺氧21 369 Nm3/h,分配风1 283 Nm3/h,中央氧1 384 Nm3/h;活度系数等热力学数据摘自文献[13-15]。铜造锍熔炼过程相平衡计算结果如表2所列。
表2 铜造锍熔炼过程相平衡计算结果
Table 2 Result of copper smelting process balance
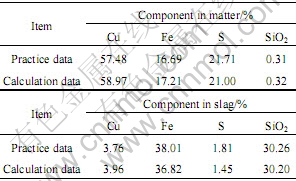
从表2可以看出,与生产实际数据相比,冰铜中Cu、Fe、S含量(质量分数,%)绝对误差分别为1.49、0.52、0.71,相对误差为2.6%、3.1%、3.3%;炉渣中Fe、SiO2、Cu含量(质量分数,%)绝对误差分别为1.19、0.06、0.2,相对误差为3.1%、0.2%、5.3%。由此可见,该方法能有效地应用于铜冶金多相平衡计算。
4 结论
1) 运用最小吉布斯函数原理和元素势概念,推导基于元素势的多相平衡计算方法,该方法具有方程少,求解速度快,且在计算过程中不会出现负摩尔分数的特点。
2) 对酯化反应多相复杂体系进行计算,其结果同文献值吻合很好,表明该方法对求解复杂化学平衡问题是有效和简单易行的。
3) 铜造锍熔炼过程多相平衡计算结果与生产实际较为吻合,表明该方法有望在冶金过程相平衡计算中得到应用。
REFERENCES
[1] 林金清, 李浩然, 韩世钧. 含化学反应体系多相平衡计算方法的研究进展[J]. 计其机与应用化学, 2003, 20(6): 724-728.
LIN Jin-qing, LI Hao-ran, HAN Shi-jun. Progress of computation method for simultaneous chemical and phase equilibrium [J]. Computers and Applied Chemistry, 2003, 20(6): 724-728.
[2] 徐辉林, 陈健, 唐宏青. 多相平衡的状态方程一步算法研究[J]. 化学工程, 2003, 31(5): 66-69.
XU Hui-lin, CHEN Jian, TANG Hong-qing. One-step algorithm for multiphase equilibrium calculation using state equations [J]. Chemical Engineering, 2003, 31(5): 66-69.
[3] 童长仁, 吴卫国, 周小雪. 铜闪速熔炼多相平衡数模的建立与应用[J]. 有色冶金设计与研究, 2006, 27(6): 6-9.
TONG Chang-ren, WU Wei-guo, ZHOU Xiao-xue. Establishment and application of multiphase equilibrium mathematical model for copper flash smelting process [J]. Nonferrous Metals Engineering & Research, 2006, 27(6): 6-9.
[4] DLUZNIEWSLI J H, ADLER S B. Calculation of complex reaction and/or phase equilibria problem [J]. International Chemical Engineering, 1972, 4: 21-26.
[5] GORDON S, MCBRIDE B J. Computer program for calculation of complex chemical equilibrium composition, rocket performance, incident and reflected shocks, and chapman- jouguet detonations [R], NASA, SP-273, Cleveland: NASA Lewis Research Center, 1971.
[6] GAUTAM R, SEIDER W D. Computation of phase and chemical equilibrium [J]. AIChEJ, 1979, 25: 991.
[7] POWELL N H, SARNAR S F. The use of element potential in analysis of chemical equilibrium [R]. R59/FPD, New York: General Electric Company, 1959.
[8] REYNOLDS W C. The element potential method for chemical equilibrium analysis: Implementation in the interactive program of STANJAN [R], TR. A-3391, California: Stanford University, 1996.
[9] 过道明, 李天祥, 叶桃红, 匡 军. 系统平衡分析的元素势法[J]. 中国科学技术大学学报, 1997, 27(1): 88-93.
GUO Dao-ming, LI Tian-xiang, YE Tao-hong, KUAN Jun. The element potential method for system equilibrium analyses [J]. Journal of China University of Science and Technology, 1997, 27(1): 88-93.
[10] 安维中, 董凤蕾, 刘晶晶, 胡仰栋, 伍联营. 应用遗传算法求解多相化学反应体系的相稳定性及平衡组成[J]. 化工进展, 2007, 26(2): 290-293.
AN Wei-zhong, DONG Feng-lei, LIU Jing-jing, HU Yang-dong, WU Lian-ying. Phase equilibria and stability calculation in multiphase reaction systems by using genetic algorithm [J]. Chemical Industry and Engineering Progress, 2007, 26(2): 290-293.
[11] MEDONALD C M, FLOUDAS C A. Global optimization for the phase and chemical equilibrium problem: Application to the NRTL equation [J]. Computers & Chemical Engineering, 1994, 19: 1111-1139.
[12] 汪金良, 卢 宏, 曾青云, 张传福. 基于遗传算法的铜闪速熔炼过程控制优化[J]. 中国有色金属学报, 2007, 17(1): 156-160.
WANG Jin-liang, LU Hong, ZENG Qing-yun, ZHANG Chuan-fu. Control optimization of copper flash smelting process based on genetic algorithms [J]. The Chinese Journal of Nonferrous Metals, 2007, 17(1): 156-160.
[13] SAKICHI G. Equilibrium calculations between matte, slag and gaseous phases in copper smelting [C]// JONES M J ed. Copper Metallurgy-Practice and Theory. London: Institute of Mining and Metallurgy, 1975: 23.
[14] 黎书华, 黄克雄, 梅显芝. 贵溪闪速炉铜锍熔炼过程热力学模型[J]. 中南工业大学学报, 1995, 26(5): 627-631.
LI Shu-hua, HUANG Ke-xiong, MEI Xian-zhi. Thermodynamic model of Guixi flash furnace process for copper matte smelting [J]. Journal of Center South University of Technology, 1995, 26(5): 627-631.
[15] 凌 玲, 沈剑韵, 陆金忠, 李 光. 镍闪速熔炼过程的平衡计算[J]. 有色金属, 2000, 52(4): 71-73.
LING Ling, SHEN Jian-yun, LU Jin-zhong, LI Guang. Equilibrium calculation for process of nickel flash smelting [J]. Nonferrous Metals, 2000, 52(4): 71-73.
基金项目:国家重大产业技术开发资助项目(20051255); 江西省科技攻关资助项目(20061B0101100); 江西省自然科学基金资助项目(2007GZC0713)
通讯作者:汪金良,博士研究生,讲师;电话: 0797-8312270;E-mail: simwjl@163.com
(编辑 李向群)