DOI: 10.11817/j.issn.1672-7207.2015.03.027
贝叶斯推论在储层渗透率预测中的应用
喻鹏,唐仲华
(中国地质大学 资源学院,湖北 武汉,430074)
摘要:以辽河油田静安堡构造带静观2块油藏为例,应用贝叶斯推论预测流动单元分布,建立基于流动单元指数分类的渗透率模型同时验证预测结果的合理性。在预测过程中,运用均分、累积概率及指数函数单增法等划分方法对测井曲线进行分类并构建二维频率交会区间,计算流动单元在各区间上的后验概率进而判别非取心井测井段的流动单元类别,对比不同条件下的预测效果并优选最佳方法,进而预测储层渗透率,最后将预测模型平面及垂向特征和油藏实际进行验证对比。实际应用表明,地质、测井知识和贝叶斯推论方法相结合,能有效判别储层流动单元类别并预测渗透率,通过对比优选不同交会条件下的预测结果,提高渗透率的预测精度,为油藏描述和表征提供更准确的地质信息。
关键词:聚类分析;流动单元;流动层带指标;测井频率交会;渗透率预测;贝叶斯推论
中图分类号:TE122.23 文献标志码:A 文章编号:1672-7207(2015)03-0970-13
Application of Bayesian theory to predict permeability of reservoir
YU Peng, TANG Zhonghua
(Faculty of Earth Resources, China University of Geosciences, Wuhan 430074, China)
Abstract: The Bayesian theory was applied to predict the distribution of hydraulic units in the Jingguan2 Block of Jinganbao oil-bearing structure belt, the permeability model was built based on the flow zone index, and the rationality of predictions was validated. The bin average, cumulative probability and exponential monotonous increase methods were applied on logs to constructure the intersection bin of 2-dimensional frequency in calculating process, and the hydraulic units of uncored wells were predicted based on the posterior probabilities of intersection bins. The best method was selected under different conditions and the permeability was predicted, and the horizontal and vertical distribution of model was validated for real reservoir conditions. The practical application shows that combining Bayesian theory with geology and well logging can not only effectively predict the hydraulic unit and permeability of reservoir, but also increase the accuracy by choosing the outstanding prediction result under different conditions, which provides more accurate geological information for reservoir description and characterization.
Key words: cluster analysis; hydraulic unit; flow zone index (FZI); logging frequency of intersection; permeability prediction; Bayesian theory
渗透率参数是储层评价中的重要参数,它的准确求取直接关系到产能的确定和储层非均质性的研究。测井、岩心分析以及地层测试等都是获取渗透率参数的重要手段,但常规测井解释方法通常由于忽略了砂岩组或单砂体内部不同流动单元之间渗透率的差异,从而导致建立的孔-渗关系达不到理想精度。至目前为止,国内外学者先后提出了很多种渗透率预测方法,如Jennings等[1]基于岩石结构系数提出了广义渗透率模型,Bryant等[2]通过地质模型预测渗透率,Mathisen等[3]借助于测井相应用数学统计方法计算渗透率,基于Kozeny-Carman方程进行储集层流动单元划分和渗透率计算,Wiener等[4]提出的多层前馈神经网络技术以及基于贝叶斯推论的渗透率预测方法等。辽河油田静观2块属高凝油油藏,储层非均质性强、碎屑物颗粒粒级较低、成分及结构成熟度较低。经过近30 a的注水开发,油藏油水关系复杂、水淹层识别困难、剩余油分布规律差,而剩余油的分布与储层渗透率关系密切[5]。为更清晰地认识储层特性,在以往工作基础上建立起更加精细的渗透率预测模型成为必然。本文作者在流动单元划分的基础上,运用贝叶斯推论求取测井二维频率交会区间上的后验概率并判别无岩心井段的流动单元类别,并结合指数及幂律关系模型对每类储层分别建立孔-渗关系式,并优选拟合优度较好的关系模型参与渗透率的预测计算。优选出的渗透率预测模型为数模精度的提高提供了基础,为油田后续的措施调整提供了科学依据。
1 地质概况
静观2区块位于辽宁省南部新民市境内,属于静安堡构造带大民屯凹陷中的一个断块(见图1)。该区块为一主轴2.8 km,次轴0.8 km,闭合面积约2.2 km2的背斜含油气断裂构造,闭合高度超过950 m。沙河街组三段中下部是研究区主要储油层,根据旋回特点及岩、电特性由下至上分为S34,S33,S32,S31 4个亚段,油层纵向上进一步细分为12个油层组,40个砂岩组,93个小层。油藏沉积环境属于断陷期扇三角洲沉积,碎屑岩发育,砂岩与泥岩间互。矿物成分以石英为主,长石次之,胶结类型以接触-孔隙式为主。平均空气渗透率0.527 μm2,孔隙度20.9%,粒度中值0.305 mm,分选系数1.63,泥质含量(体积分数)7.16%。油藏纵向上渗透率随深度变化明显,埋深越大渗透率越小;平面上渗透率受沉积相带控制,河道微相渗透性明显好于河间薄层砂微相。层内、层间及平面非均质性均较强。
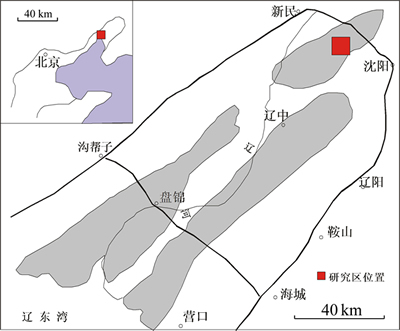
图1 辽河油田静观2块研究区位置图
Fig. 1 Well location indicated of Jingguan2 Block in Liaohe Oilfield
2 数学背景
2.1 储层流动层带指标(FZI)
Amaefule等[6]基于油藏渗透率的变化特征,提出运用水动力单元法来划分岩石相和单井相。该方法将总的油藏岩石体积中影响流体流动的地质和油层物理性能恒定不变并且可以与其他岩石体积区分开来的具有代表性的基本体积(REV)定义为孔隙几何单元。他们把油藏孔隙空间看作是一系列的毛细管,结合Darcy定理,得出表征不同流动单元间孔隙度及渗透率关系的方程[7]:
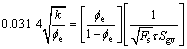 (1)
(1)
式中:k为渗透率(10-3 μm2); 为有效孔隙度;Fs为孔隙形状系数;τ为孔隙介质的迂曲度;Sgv为单位颗粒体积比表面(μm-1)。
为有效孔隙度;Fs为孔隙形状系数;τ为孔隙介质的迂曲度;Sgv为单位颗粒体积比表面(μm-1)。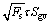 为关于多孔介质地质特征的函数,随孔隙及其性质变化[8]。表征流动单元的指标参数表达式如下:
为关于多孔介质地质特征的函数,随孔隙及其性质变化[8]。表征流动单元的指标参数表达式如下:
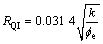 (2)
(2)
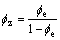 (3)
(3)
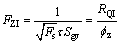 (4)
(4)
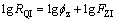 (5)
(5)
式中:RQI为储层品质指数(μm);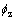 为标准化孔隙度指数;FZI为储层流动层带指标(μm)。
为标准化孔隙度指数;FZI为储层流动层带指标(μm)。
方程(2)~(4)可计算出双对数坐标体系中RQI及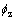 的关系式(式5)。具有相同FZI的样品将落在同一直线上,直线斜率为1,平均FZI即单位斜线坐标
的关系式(式5)。具有相同FZI的样品将落在同一直线上,直线斜率为1,平均FZI即单位斜线坐标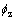 =1时的截距。因此,同一直线上的样品具有相似的孔喉特征,归属同一流动单元[9]。统计学方法证明孔隙几何属性可以影响流动单元分带,FZI能有效判别具有相似流动属性特征的岩石相。
=1时的截距。因此,同一直线上的样品具有相似的孔喉特征,归属同一流动单元[9]。统计学方法证明孔隙几何属性可以影响流动单元分带,FZI能有效判别具有相似流动属性特征的岩石相。
通过上述公式可以看出,储层流动层带指标的概念结合了矿物结构、岩石地质及孔喉特征来判定孔隙几何形态,可以准确地描述油藏的非均质性[10-11]。
2.2 基于测井曲线多维频率交会的贝叶斯推论
运用贝叶斯推论预测渗透率的基础是建立HU(Hydraulic unit)后验概率库。概率库的构建则以岩心分类资料及测井响应信息为基础。式(7)代表多测井曲线交会的后验概率。运用贝叶斯推论对取心井段的流动单元建立后验概率库,进而对没有岩心井段的流动单元及渗透率进行判别和预测。判别过程中测井参数的区间划分也同时影响流动单元的预测精度。
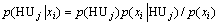 (6)
(6)
式中:p(xi)为p(x1∩x2…∩xn)的多曲线交会概率;p(HUj)为流动单元j在多曲线交会总域上的先验概率;p(xi|HUj)为流动单元j发生条件下x1∩x2…∩xn的条件概率;p(HUj|xi)为HUj的后验概率。
3 流动单元分类及其预测
根据静观2块3口密闭取心井(J63-21,J64-16,JG1)的岩心及测井资料,运用分层随机抽样法选取810个样本点进行流动单元分类研究,确保所选样点覆盖整个孔渗区间。
3.1 流动单元HU分类
依据研究靶区油藏地质情况,用压汞分析资料建立FZI与排驱压力(Pd)的关系,流动层带指标与反应微观孔隙结构特征的参数相关性高,故选取FZI同时辅以流动单元特征参数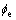 ,
, 及RQI进行聚类,分析过程中选用Ward提出的系统聚类法。该方法主要为样品聚类而设计,聚类效果好,对孤立点的处理合理[12-13]。聚类过程中考虑接近样本点特征的同质性,将储层流动单元分类划分出4种合理方案(HU#5,HU#6,HU#7,HU#8)。
及RQI进行聚类,分析过程中选用Ward提出的系统聚类法。该方法主要为样品聚类而设计,聚类效果好,对孤立点的处理合理[12-13]。聚类过程中考虑接近样本点特征的同质性,将储层流动单元分类划分出4种合理方案(HU#5,HU#6,HU#7,HU#8)。
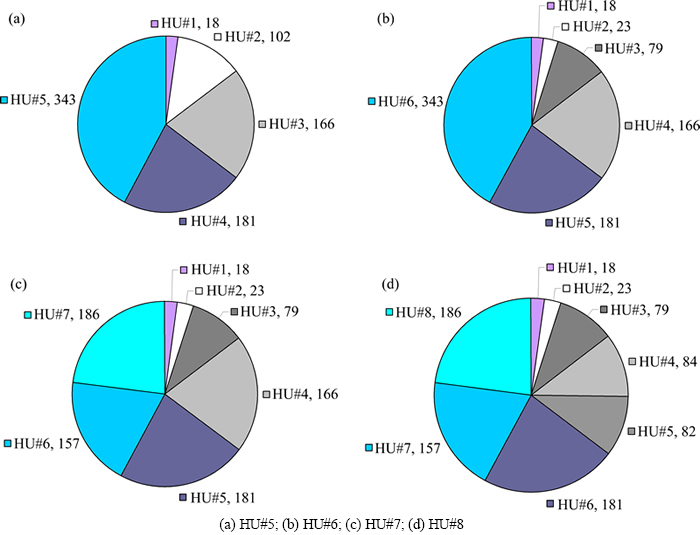
图2 流动单元取心样本点数聚类统计结果
Fig. 2 Statistical clustering results of core samples in hydraulic units
图3所示为取心样本流动单元分类结果。图4所示为岩石物理相法验证下的孔-渗关系。从图3可以看出,各流动单元区分明显且在斜率为1的一簇直线附近呈规律性分散,直线截距即为对应流动单元类别的FZI。由以FZI分类为基础计算的取心井段渗透率和实测渗透率的相关性分析得出,随着HU分类数的增加,kHU和kcore的相关性逐渐变好,尤其在渗透率高值部位,呈现出了较高的相关性(CHU#5=0.937 0,CHU#6= 0.950 1,CHU#7=0.965 8,CHU#8=0.989 2),这与该区复杂的岩性分类状况相匹配。运用孔喉半径R35法结合Winland公式对储层4种不同的聚类结果进行验证(图4),工区范围内孔喉半径的分布规律显示R35和孔隙度、渗透率关系密切,亦证明Ward聚类法划分的流动单元流体流动特征符合工区储层特点[14]。
3.2 流动单元HU预测
由于区域地质背景不同,储层各种测井曲线的响应特征也存在差异[15]。因此,首先运用Spearman非参数相关系数法对3口取心井的测井参数及FZI进行相关分析(表1)。参与计算的测井曲线包括声波时差(AC)、自然电位(SP)、自然伽马(GR)及地层真电阻率(RT)等。利用线函转换法转换后的GR曲线计算的地层泥质含量φsh也同时参与计算。测井曲线RT和φsh在单井及总样本中都呈现出较高的相关性,优选这2类曲线进行流动单元的推导预测。
运用概率累积分布函数求取φsh的累积概率,并将数据区间划为8类,同时,运用均分法、累积概率分段法以及指数函数单增法等划分法对测井数据RT进行区间分类,并将分类后的区间分别定义为φsh-A,8;RT-A,8;RT-B,8;RT-C,8(表2~3)。将测井二维频率交会项分别定义为1(φsh-A和RT-A),2(φsh-A和RT-B),3(φsh-A和RT-C)。
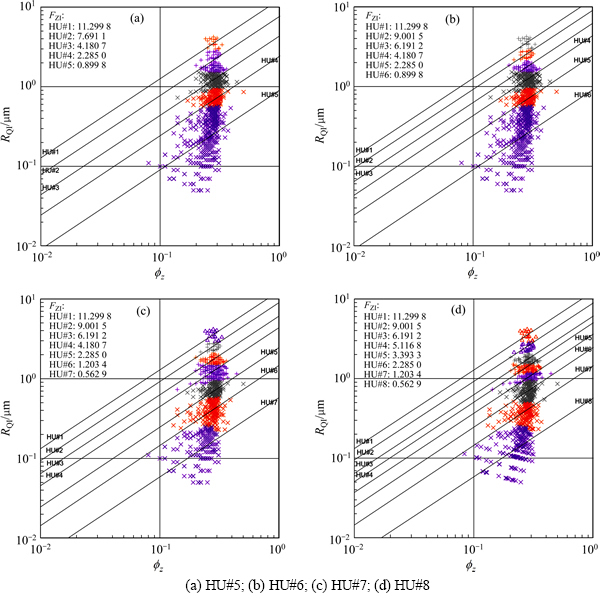
图3 取心样本流动单元分类结果
Fig. 3 Hydraulic units partition of core samples
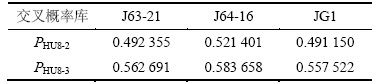
图6所示为不同概率库条件下预测渗透率效果对比。运用贝叶斯推论计算每个测井频率交会区间内样本点HU出现的后验概率:PHU5-1,PHU5-2,PHU5-3;PHU6-1,PHU6-2,PHU6-3;PHU7-1,PHU7-2,PHU7-3;PHU8-1,PHU8-2,PHU8-3。概率库构建执行过程中,对不同流动单元出现在各交会区间上的概率进行统计,优选最大后验概率值对应的流动单元类别作为本区间的基事件,进而判别非取心井各测井点段对应的HU类别并结合式(6)预测渗透率。为检验判别效果,通过后验概率库回判预测取心井段的HU及渗透率,并将计算渗透率和岩心渗透率进行拟合优度对比检验,结果证明HU8-2及HU8-3的应用效果较好(图6)。
图7所示为单井预测HU检验频数配位统计,图8所示为相控条件约束下的流动单元地质模型。在优选的预测方法HU8-2及HU8-3的基础上,统计对比每类预测流动单元及岩心流动单元匹配的频数。图7反映出HU8-2及HU8-3匹配柱状图中频数配位较高值基本集中于主对角线上,证明在测井二维频率交会的基础上运用贝叶斯推论进行流动单元的推导方法具有一定合理性。表4所示为基于2种不同概率库推导流动单元种类的正判率。从表4可以看出:后验概率库PHU8-3对HU的正判率比PHU8-2高,单井流动单元及渗透率的预测结果亦表明HU8-3的结果更贴近油藏实际(图8)。
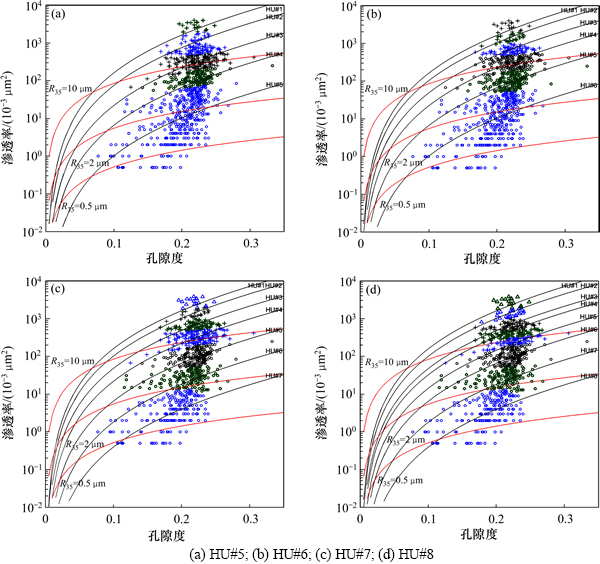
图4 岩石物理相法验证下的孔-渗关系
Fig. 4  delineation and relationship plot with petrophysical theory verification
delineation and relationship plot with petrophysical theory verification
表1 取心井测井响应参数和FZI相关分析数据
Table 1 Correlation well log responses with F ZI of cored wells

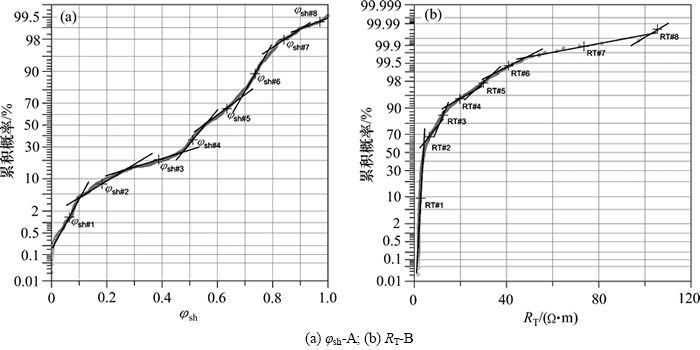
图5 测井响应参数累积概率曲线
Fig. 5 Cumulative probability curves of log responses
表2 φsh的累积概率分类区间
Table 2 φsh bins for partitioning method of cumulative probability

表3 不同划分法对应测井响应RT的分类区间
Table 3 RT bins for different partitioning methods

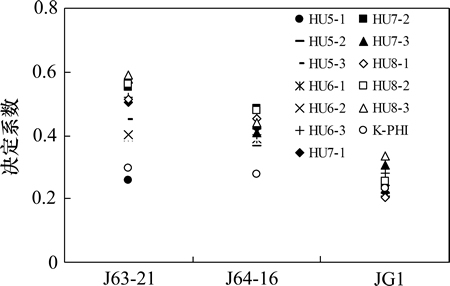
图6 不同概率库条件下预测渗透率效果
Fig. 6 Permeability prediction effect under different probability databases
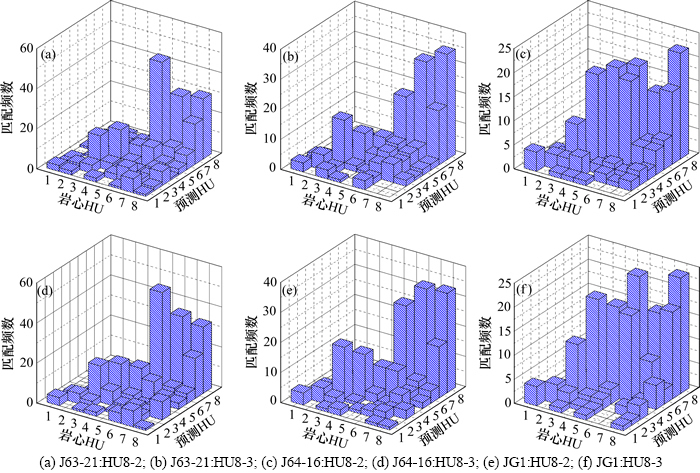
图7 单井预测HU检验频数配位统计
Fig. 7 Statistical results of frequency of prediction HU for single well
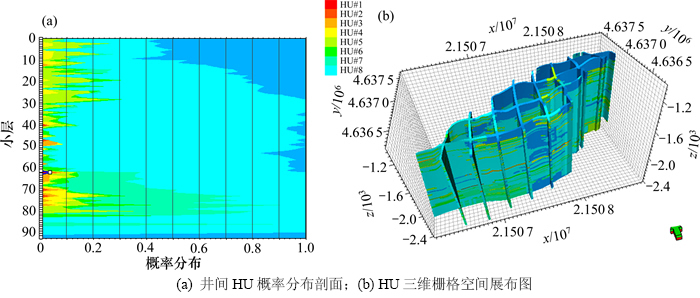
图8 相控条件约束下的流动单元地质模型
Fig. 8 Facies-controlled hydraulic unit geological model
表4 基于2种不同概率库推导流动单元种类的正判率
Table 4 Distinguishing-positive rates of HU based on different probability databases
3.3 流动单元HU预测模型的建立
运用序贯指示模拟方法建立储层流动单元预测模型。序贯指示模拟的基本思路是:利用待估点周围的点信息,建立待估点处的条件概率分布,然后通过蒙特卡洛抽样获得待估点处的值,该值将作为条件数据应用于其他未估点。当所有未估点都有估值时,就取得了一次实现[16-17]。
图9所示为孔隙度-渗透率预测回归模型。根据贝叶斯推论计算的测井交会后验概率库判别工区27口井(含3口取心井未取心段)各深度点段HU,并将流动单元作为8类离散型变量处理,应用序贯指示模拟的方法,建立起流动单元预测模型。在随机建模过程中,以沉积微相外边界作为控制,同时根据储层地质背景选用相应的变差函数模型,通过选取不同的随机路径,获得多个等可能、等概率的实现。将实现结果和实际资料对比,最终优选与实际资料最符合的模型作为HU预测模型[18-19],含纵向小层93层(图8)。
3.4 渗透率预测模型的建立
针对一些具有特殊性质的油藏,应用传统的渗透率预测方法常由于孔渗数据过于发散而显示出悲观的渗透率值。以靶区强非均质性复杂断块油藏为例,在传统预测法实施的过程里常在总孔隙度与渗透率的首要关系中,忽略了储层非均质性对渗透率的重要影响。将流动单元类别划分结果和渗透率模型相结合,分别对每类流动单元的渗透率进行预测,可在一定程度上降低渗透率级差大所带来的误差,提高模型的解释精度[20]。
根据储层岩心流动单元的分类,运用指数及幂律关系模型对每类储层分别建立渗透率-孔隙度关系式,并优选拟合优度较好的关系模型参与渗透率的预测计算(图9)。
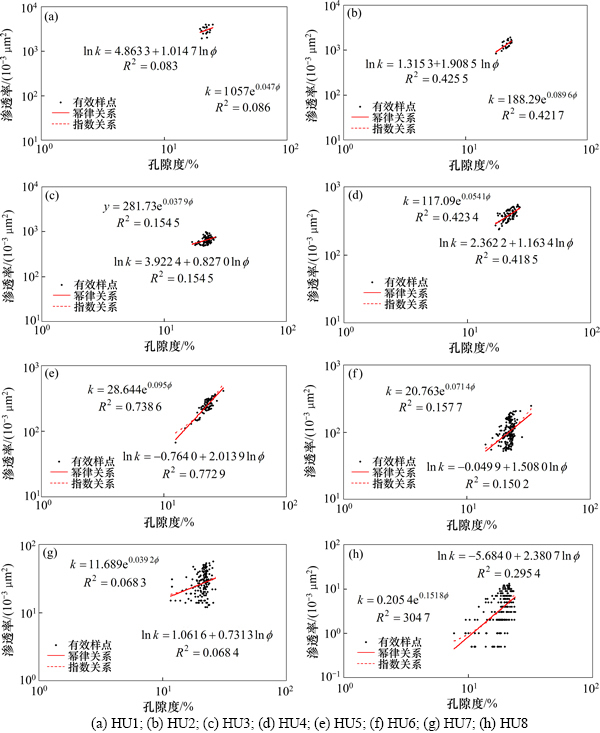
图9 孔隙度-渗透率预测回归模型
Fig. 9 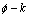 regression forecast model
regression forecast model
研究中采用的数学模型为:
HU#1: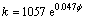 (R2=0.086)
(R2=0.086)
HU#2: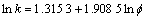 (R2=0.425 5)
(R2=0.425 5)
HU#3: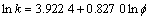 (R2=0.154 5)
(R2=0.154 5)
HU#4: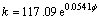 (R2=0.423 4)
(R2=0.423 4)
HU#5: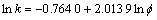 (R2=0.772 9)
(R2=0.772 9)
HU#6: (R2=0.157 7)
(R2=0.157 7)
HU#7: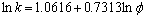 (R2=0.068 4)
(R2=0.068 4)
HU#8: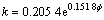 (R2=0.304 7)
(R2=0.304 7)
式中:k为渗透率(10-3 μm2); 为孔隙度(%)。
为孔隙度(%)。
图10所示为静观2块油藏渗透率预测模型。运用地质建模软件Petrel中的计算模块,调用if语句,将以上数学模型分别匹配给每个流动单元网格,计算出每个网格的渗透率值。
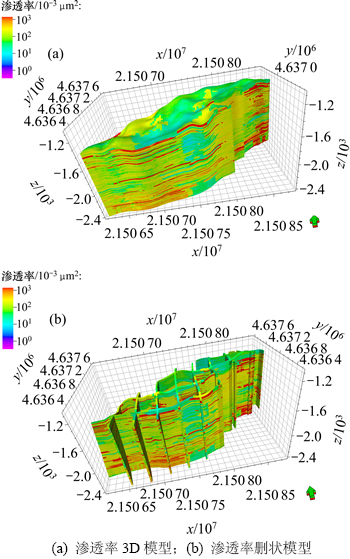
图10 静观2块油藏渗透率预测模型
Fig. 10 Permeability prediction model of Jingguan2 Block
4 渗透率预测模型合理性验证
4.1 模型平面验证
图11所示为渗透率在xy方向上的变差函数平面图,图12所示为变差函数图。流动单元内渗透率的方向性对流体的运动影响较大,非均质方向性主要通过流动单元内的岩性变化而形成,通过研究储集体主体带与边缘带、高能带与低能带的差别可揭示流动单元非均质性的方向性。基于已建立的渗透率模型反求变差函数,通过其在xy方向上的变差平面图可以看出:主变程方向和北东向沉积物源方向较为吻合,基台值(Sill)为0.951 0,块金值(Nugget)为0.295 1,最大变程为899.69 m,最小变程为451.92 m(图11~12),这和各沉积相的发育规模比较吻合。
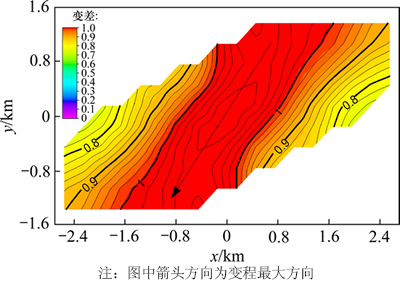
图11 渗透率在xy方向上的变差函数平面图
Fig. 11 Variogram figure in xy of permeability
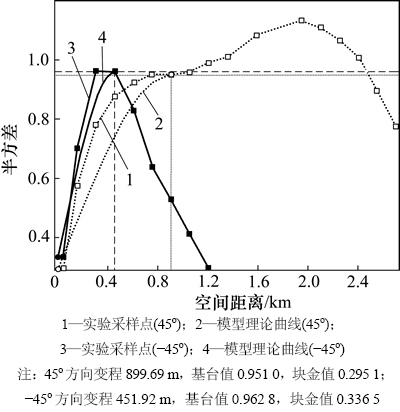
图12 变差函数图
Fig. 12 Variogram figure
图13所示为静观2块小层孔-渗-沉积微相平面关系对比。从平面分布模型来看,各小层渗透率的总体分布特征与砂体骨架有较好的对应关系,即高渗透带位于厚层砂体的主体部位。从工区小层孔-渗平面关系对比图可以发现(图13),二者之间具有一定对应关系,即高值对高值,低值对低值,但又不是严格的一一对应。如边界断层附近出现少量渗透率极低值,与孔隙度匹配较差,主要由于流动单元指示模拟时缺少井点控制造成。
综上,工区渗透率预测模型平面总体分布特征与沉积相发育规模及其对应的孔隙度平面特征具有一定关联性,整体预测效果较好。
4.2 模型垂向验证
图14所示为沉积相剖面和渗透率预测剖面对比。运用钻井抽稀的验证方法,从工区78口井中剔除6口数据井(J63-21,J63-321,J64-16,J65-123,J65-519,JG1),重复之前建模思路结合序贯指示模拟的方法重建渗透率三维地质模型。以3口验证井连线为轴线切取渗透率剖面和沉积相联井剖面对比,从图14可以看出:渗透率值和沉积模型剖面有一定对应关系,泥岩发育区,渗透率呈低值状态,河道砂剖面部位渗透率值平均较高。
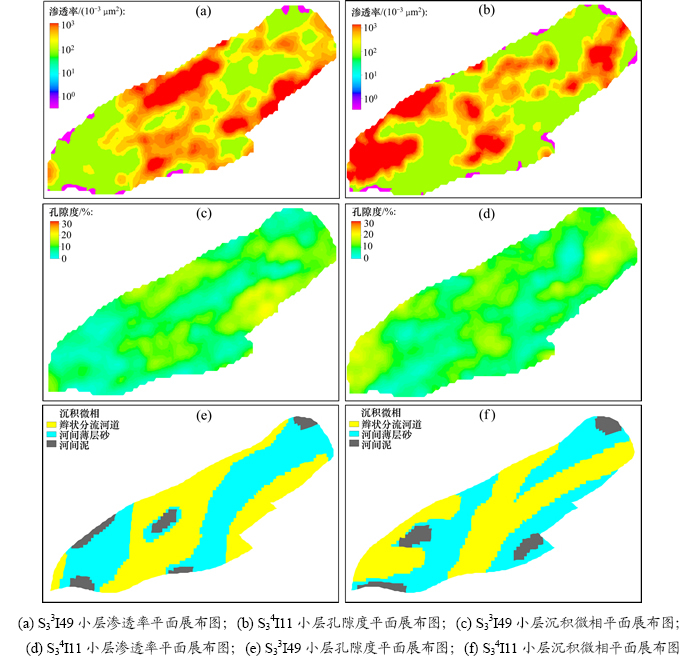
图13 静观2块小层孔-渗-沉积微相平面关系对比
Fig. 13 k-Ф-Facies relationship of Jingguan2 Block
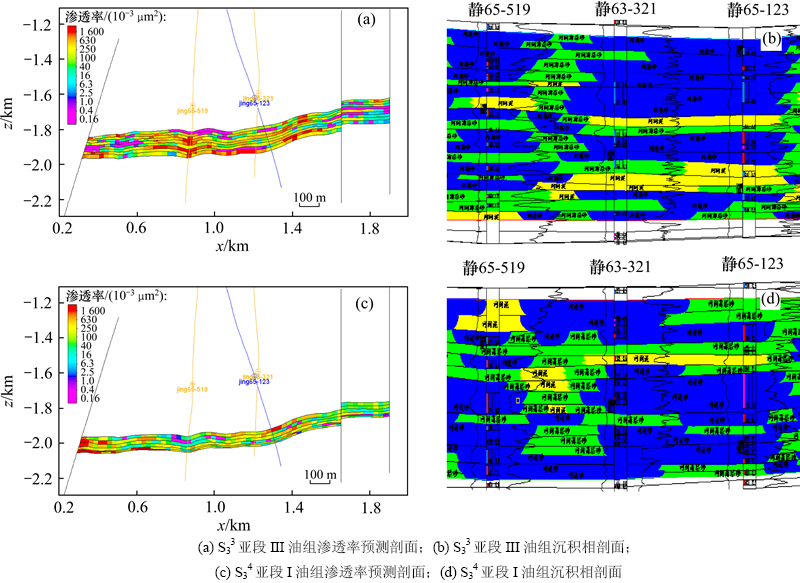
图14 沉积相剖面和渗透率预测剖面对比图
Fig. 14 Profile of sedimentary and permeability
图15所示为预测模型垂直方向的变差。变程约5.02 m,同砂体垂向发育规模吻合较好。过原点处变差值呈跳跃状,亦证明该区的强非均质性。为定量研究预测结果和油藏实际拟合精度,进一步通过抽稀井的预测,得出J63-21,J64-16及JG1这3口验证井的渗透率预测剖面。
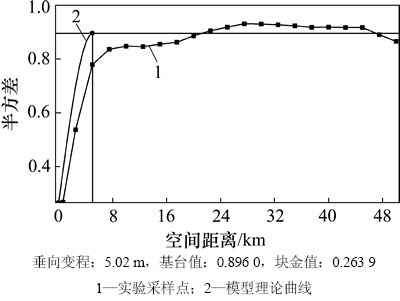
图15 垂直方向的变差
Fig. 15 Variogram of vertical direction
图16所示为渗透率预测剖面。从渗透率剖面上看(图16):除少数极值点外,预测值基本同岩心数据吻合,即原始数据和抽稀地质模型中对应数值相对误差较小。同时,抽稀前后整个地质模型的统计特征也基本保持一致,表明抽稀对模型精度影响不明显,即在保持已知确定性信息延续的基础上对模型进行验证具有一定合理性。
5 结论
1) 测井数据分区是构建后验概率库的基础,由于区域地质背景不同,不同储层测井参数适用的划分方法也不尽相同。流动带指标样本点可能呈现指数、逻辑甚至线性规律聚簇,而现实中的聚簇规律模糊,往往需通过判别后的结果得到。该区由指数递增法划分的RT曲线区间中样本点呈现的聚簇规律最强,同物性由好到差样本点逐渐增多的油藏实际趋势规律相一致,预测效果优于均分法和累积概率分段法。
2)选取测井响应二维频率交会区间推导预测储层流动单元,该方法亦可包含测井曲线的多维频率交会。通过建立测井曲线与FZI的相关性,优选相关系数高的测井项个数为频率交会维数,最大程度贴近真实地质情况,可提高预测精度。
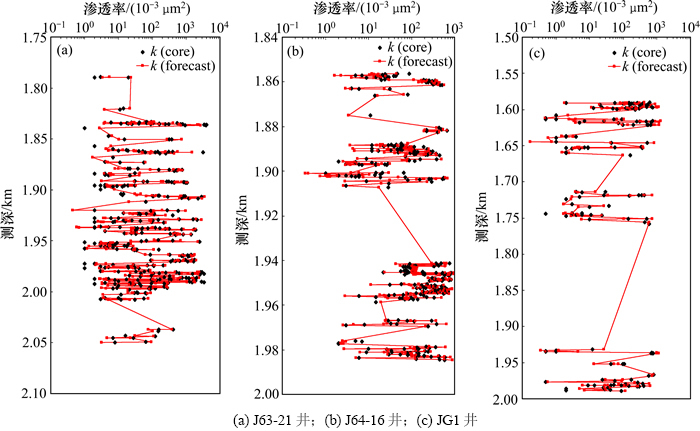
图16 渗透率预测剖面
Fig. 16 Profile of permeability prediction
3) 流动单元的边界不总与岩石物理相的边界一致。该区流动单元被划分为8类,每类流动单元都对应有其特有的岩性组合及流动特征。
4) 对于非均质性严重的储层,同一孔隙度值下渗透率级差大,传统方法建立的渗透率模型无法满足储层评价要求。在划分流动单元的基础上运用贝叶斯推论建立后验概率库进而推导HU及储层渗透率,预测精度较高,可在具有相似区域地质背景的区块上推广试用。
参考文献:
[1] Jennings Jr J W, Lucia F J. Predicting permeability from well logs in carbonates with a link to geology for interwell permeability mapping[J]. SPE Reservoir Evaluation & Engineering, 2003, 6(4): 215-225.
[2] Bryant S, Cade C, Mellor D. Permeability prediction from geologic models[J]. The American Association of Petroleum Geologists, 1993, 77(8): 1338-1350.
[3] Mathisen T, Lee S H, Datta-Gupta A. Improved permeability estimates in carbonate reservoirs using electrofacies characterization: A case study of the north Robertson unit, West Texas[J]. SPE Reservoir Evaluation & Engineering, 2003, 6(3): 176-184.
[4] Wiener J, Rogers J A, Rogers J R, et al. Predicting carbonate permeabilities from wireline logs using a back-propagation network[C]// Proceedings of the 61st SEG meeting. Houston: SEG, 1991: 285-288.
[5] 谭锋奇, 许长福, 韦雅, 等. 基于是值模拟的水淹储层原始电阻率反演方法[J]. 中南大学学报(自然科学版), 2012, 43(8): 3149-3158.
TAN Fengqi, XU Changfu, WEI Ya, et al. Original resistivity inversion method of flooded reservoir based on numerical simulation[J]. Journal of Central South University (Science and Technology), 2012, 43(8): 3149-3158.
[6] Amafule J O, Altunbay M, Laboratories C, et al. Enhanced reservoir description: Using core and log data to identify hydraulic(flow) units and predict permeability in uncored intervals/wells[C]// Proceedings of SPE Annual Technical Conference and Exhibition. Houston: SPE, 1993: 1-16.
[7] Abbaszadeh M, Fujii H, Fujimoto F. Permeability prediction by hydraulic flow units: Theory and applications[J]. SPE Formation Evaluation, 1996, 11(4): 263-271.
[8] 李伟才, 姚光庆, 周锋德, 等. 低渗透油藏不同流动单元并联水驱油[J]. 石油学报, 2011, 32(4): 658-663.
LI Weicai, YAO Guangqing, ZHOU Fengde. Water displacing oil efficiency with cores grouped in parallel of different flow units in low-permeability reservoirs[J]. Acta Petrolei Sinica, 2011, 32(4): 658-663.
[9] 尹太举, 张昌民, 王寿平, 等. 濮53块流动单元评价[J]. 石油学报, 2005, 26(5): 85-89.
YIN Taiju, ZHANG Changmin, WANG Shouping, et al. Estimation of flow units in Pu-53 Block[J]. Acta Petrolei Sinica, 2005, 26(5): 85-89.
[10] Hearn C L, Ebanks W J Jr, Ranganathan V, et al. Geological factors influencing reservoir performance of the hartzog draw field wyoming[J]. J Pet Technol, 1984, 36(9): 1335-1344.
[11] Ebanks W J Jr. Flow unit concept: An integrated approach to reservoir description for engineering projects[J]. AAPG Bulletin, 1987, 71(5): 551-552.
[12] 邱苏林, 王丽珍. 基于Ward’s方法的k-平均优化算法及其应用[J]. 计算机工程与应用, 2008, 44(31): 169-172.
QIU Sulin, WANG Lizhen. Modified k-means algorithm based on Ward’s method and application[J]. Computer Engineering and Applications, 2008, 44(31): 169-172.
[13] 赵骅, 朱莉华, 刘丹. Ward系统聚类法在多变量分层抽样技术中的运用[J]. 统计与决策, 2006, 22(12): 67-68.
ZHAO Hua, ZHU Lihua, LIU Dan. Application of Ward hierarchical clustering method in the technique of multivariate stratified sampling[J]. Statistics and Decision, 2006, 22(12): 67-68.
[14] 李楚吟, 陈维华, 付崖梅, 等. 利用流动单元指数进行储层分类评价[J]. 中外能源, 2012, 17(10): 40-43.
LI Chuyin, CHEN Weihua, FU Yamei, et al. The application of flow units index in reservoir classification evaluation[J]. Sino-Global Energy, 2012, 17(10): 40-43.
[15] 方雪芹, 刘德菊, 田军, 等. 测井资料在松辽盆地岩性储层预测中的应用[J]. 石油物探, 2007, 46(5): 496-500.
FANG Xueqin, LIU Deju, TIAN Jun, et al. Application of logging data in lithology reservoir prediction in Songliao Basin[J]. Geophysical Prospecting for Petroleum, 2007, 46(5): 496-500.
[16] Martin A J, Solomon S T, Hartmann D J. Characterization of petrophysical flow units in carbonate reservoirs[J]. AAPG Bulletin, 1997, 81(5): 734-759.
[17] 李海燕, 彭仕宓, 刘风喜. 储层动态流动单元研究: 以别古庄油田京11断块为例[J]. 油气地质与采收率, 2007, 14(2): 67-70.
LI Haiyan, PENG Shimi, LIU Fengxi. Reservoir dynamic flow unit models of Jing11 block in Bieguzhuang Oilfield[J]. Petroleum Geology and Recovery Efficiency, 2007, 14(2): 67-70.
[18] 严科, 杨少春, 任怀强. 基于油藏开发动态的储层四维模型的建立[J]. 中国石油大学学报(自然科学版), 2010, 34(1): 12-17.
YAN Ke, YANG Shaochun, REN Huaiqiang. Building of 4D reservoir model based on development performance[J]. Journal of China University of Petroleum (Edition of Natural Science), 2010, 34(1): 12-17.
[19] 陈烨菲, 彭仕宓, 宋桂茹. 流动单元的井间预测及剩余油分布规律研究[J]. 石油学报, 2003, 24(3): 74-77.
CHEN Yefei, PENG Shimi, SONG Guiru. Inter-well prediction of flow units and remaining oil distribution[J]. Acta Petrolei Sinica, 2003, 24(3): 74-77.
[20] 焦翠华, 徐朝晖. 基于流动单元指数的渗透率预测方法[J]. 测井技术, 2006, 30(4): 317-319.
JIAO Cuihua, XU Zhaohui. An approach to permeability prediction based on flow zone index[J]. Well Logging Technology, 2006, 30(4): 317-319.
(编辑 陈爱华)
收稿日期:2014-05-09;修回日期:2014-08-10
基金项目(Foundation item):国家油气重大专项(2011ZX05009-002) (Project(2011ZX05009-002) supported by the National Major Program of Oil & Gas)
通信作者:喻鹏,博士研究生,从事油气田开发地质方面的研究;E-mail: developoil@163.com