一种水上行走机器人的模糊控制
王淑慧1,吴立成2,袁海文1
(1. 北京航空航天大学 自动化科学与电气工程学院,北京,100191;
2. 中央民族大学 信息工程学院,北京,100081)
摘要:为了实现水上行走机器人的自主行走,讨论了水上行走机器人基于红外传感器的模糊控制算法问题,建立了水上行走机器人的运动学模型及执行器(电机)的动力学方程。考虑到水上行走机器人运动的非完整性以及其动力学难以精确建模,本文采用模糊控制。在对传感器数据进行标定并拟合电机电压与转速关系的基础上,设计模糊控制器实现了机器人对光源目标的趋近和轨迹跟踪,最后利用Matlab/Simulink进行仿真。仿真结果验证了该算法的准确性和有效性,说明该控制器性能良好。
关键词:水上行走机器人;模糊控制;自主运动
中图分类号:TP242 文献标志码:A 文章编号:1672-7207(2011)S1-0079-06
Fuzzy control of a kind of water strider robot
WANG Shu-hui1, WU Li-cheng2, YUAN Hai-wen1
(1. School of Automation Science and Electrical Engineering, University of Aeronautics and Astronautics,
Beijing 100191, China;
2. School of Information Engineering, Minzu University of China, Beijing 100081, China)
Abstract: To make water strider robot (WSR) walk on the water, the fuzzy control method is discussed. The kinematics model of the WSR and dynamics equations concerning the actuator (motor) are established. Considering the motion's non-holonomic feature of the WSR and inaccurate equations, a fuzzy control method is applied. After calibration of the sensor, on the basis of fitting motor voltage and rotation speed, a fuzzy controller is developed to allow the robot approaching the light source target and tracking the trajectory of the target. Finally Matlab/Simulink is used to simulate autonomous motion of water strider robot. Simulation results show the effectiveness and accuracy of the approach.
Key words: water strider robot; fuzzy control; autonomous motion
水上行走机器人的研究在国际上刚刚起步[1]。目前的研究都还没有实现自主行走,也未见运动控制方面的内容。为了研制具有一定自主行走能力的新一代机器人,研究机器人的动力学建模和运动控制问题就显得非常重要。水上行走机器人与轮式移动机器人的运动模式类似,后者的研究比较成熟,其研究方法可以借鉴。轮式移动机器人的控制大多是基于运动学模型的[2-5]。水上行走机器人工作在特殊的水面运行环境,要获得良好的控制效果,需要专门研究其控制器设计问题。本文建立了水上行走机器人的运动学模型及执行器(电机)的动力学方程。考虑到水上行走机器人运动的非完整性以及方程本身并不精确,采用模糊控制实现系统的控制较可行[6-8]。机器人通过两个红外传感器来感知本体位姿,在对传感器数据标定并拟合电机电压与转速关系的基础上,设计模糊控制器实现机器人对光源目标的趋近和轨迹跟踪,最后利用Matlab/Simulink仿真了水上行走机器人的自主运动。
1 机器人建模
1.1 机器人系统描述
以水上行走机器人“Water Dancer II-a”作为分析和控制对象,如图1所示。机器人包括机器人本体、控制电路板、驱动系统(电机)、支撑腿和驱动腿。其中控制电路板集成了红外传感器、控制器、串口通讯等。机器人总体结构呈对称分布,通过合理安排器件的位置使机器人重心位于控制板的几何中心。机器人通过支撑腿在水面的表面张力支撑,驱动腿与电机输出轴相连,旋转时划动水面产生动力,从而实现了机器人在水上行走。机器人通过放置在前端两侧的2个红外传感器读取实验环境下红外光源信号,判断自身位置,并按照一定方式行走,从而实现了运动的自主控制。

图1 Water Dancer II-a图
Fig.1 Photo of water Dancer II-a
1.2 机器人运动学模型
如图2所示,xOy为惯性坐标系,并以机器人几何中心点为原点建立动坐标系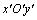 。机器人位置和姿态分别表示为
。机器人位置和姿态分别表示为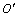 的坐标和从x轴到
的坐标和从x轴到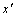 轴的夹角
轴的夹角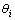 ,则i时刻机器人位姿可表示为(xi, yi, θi)。设机器人i时刻从点M出发,经过1个控制周期T,于i+1时刻到达点N,期间左、右轮速度分别为vL和vR,则机器人线速度和角速度分别为
,则i时刻机器人位姿可表示为(xi, yi, θi)。设机器人i时刻从点M出发,经过1个控制周期T,于i+1时刻到达点N,期间左、右轮速度分别为vL和vR,则机器人线速度和角速度分别为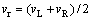 ,
,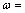
 ,机器人走过的弧长、转过的角度和所走圆弧的半径分别为
,机器人走过的弧长、转过的角度和所走圆弧的半径分别为 ,
, 和
和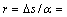
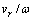 ,因此,机器人走过的直线距离为
,因此,机器人走过的直线距离为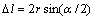 ,最终可得M点在动坐标系
,最终可得M点在动坐标系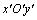 中的坐标为
中的坐标为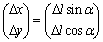 。因此,i+1时刻机器人位姿可表示为:
。因此,i+1时刻机器人位姿可表示为:
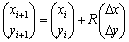
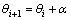 (1)
(1)
其中: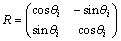 。
。
如图2所示,2个红外传感器分别位于机器人前端的两侧,在动坐标系中的坐标分别为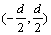 和
和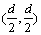 ,绝对坐标为:
,绝对坐标为:
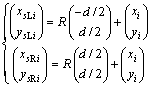 (2)
(2)
仿真中传感器与光源的距离l1和l2可根据传感器坐标和光源坐标计算得到。
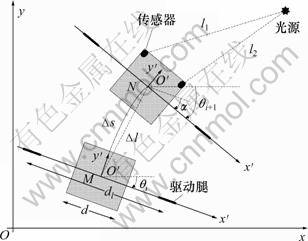
图2 机器人坐标系统示意图
Fig.2 Schematic diagram of robot coordinate system
1.3 执行器动力学方程
机器人采用2个永磁直流电动机驱动,由其转速特性可得:
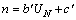 (3)
(3)
式中: 和
和 均为常数,均与电机固有参数有关,详细推导可参考文献[9];n为电机转速(r/min);UN为电机外加额定电压。式(3)表明:n和UN呈线性关系。
均为常数,均与电机固有参数有关,详细推导可参考文献[9];n为电机转速(r/min);UN为电机外加额定电压。式(3)表明:n和UN呈线性关系。
图3所示为驱动腿划水示意图。图3中:h为驱动腿中心轴到水面的高度,驱动腿速度为v。机器人的驱动腿采用细钢丝制成,质量非常小;电动机加上驱动腿负载时的转动线速度可以近似为空载时的转动线速度,即驱动腿的转动线速度为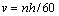 ,代入式(3)可得:
,代入式(3)可得:
 (4)
(4)
式中: ;
;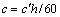 ;b和c均为常数。式(4)表明:v和UN呈线性关系。
;b和c均为常数。式(4)表明:v和UN呈线性关系。
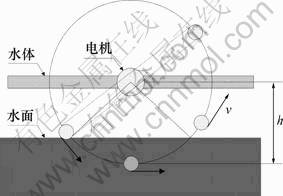
图3 驱动腿划水示意图
Fig.3 Diagram of driving legs paddling movement
1.4 传感器及电机标定
“Water DancerⅡ-a”本体大小为0.03 m×0.03 m,位于前端两侧的2个红外传感器接收实验装置中红外点光源信号,转换为电压,传感器为PT204-6B型号的红外传感器。由光学原理[10]可知,点光源传播到近处为球面波。球面波的光强与距离平方成反比,即I=A/r2 (A为常数)。由此式可知:2个传感器转换得到的电压与其到光源的距离的平方成反比。实验中采用小功率红外发光二极管作为红外光源来对传感器进行标定。通过电路测定距光源一定距离下的传感器输出电压,在0.2~1.5 m范围内,每隔0.1 m测1个点,共测得14个数据对,如图4所示。实验表明:传感器在距光源0.3~1.5 m的范围内能够产生有意义的输出,输出电压的最大最小值分别为0.1 V和2.8 V。采用多项式函数标定电压和距离的函数关系,拟合得到的曲线方程为: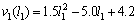 。见图4。
。见图4。
由式(3)可知:n和UN理论上呈近似线形关系,实验中所使用的微小型电机,其产品参数未包含比例系数b和c。因此,需通过电路测量,本文采用的测量电路如图5所示。
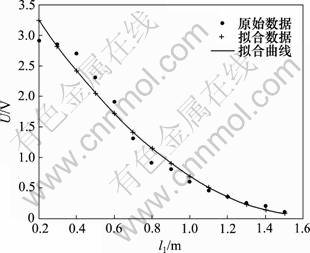
图4 红外传感器电压与距离关系
Fig.4 Voltage vs distance of infrared sensor
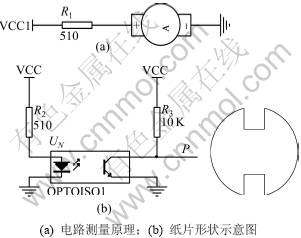
图5 电机转速与电压关系测量电路图
Fig.5 Measurement circuit diagram of motor speed and voltage
图5(a)中,光电对管工作原理是:左边二极管导通发射红外光,若中间无遮挡,右边三极管将接收红外光,处于导通状态,P点为低电平;若中间有遮挡,右边三极管无法接收红外光,处于禁止状态,P点为高电平。利用该原理可以测量电机的转速。将电机输出轴连接一个两端开有凹槽的纸片,形状如图5(b)所示,将其置于光电对管的凹槽内,电机转动,纸片凹槽通过光电对管中间时,三极管导通,P为低电平,否则P为高电平。通过测量P点信号变化的频率即可得到电机的转速,其关系为:fV=2n。其中:fV为信号频率;n为电机转速。
通过电路测定一定电压下的电机转速,测得该型电机起转电压约为0.5 V。在0.5~1.5 V范围内,每隔0.1 V测1个点,共测得11个数据对,如图6所示。采用多项式函数标定电压和电机转速的关系,拟合得到的曲线方程为:
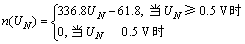
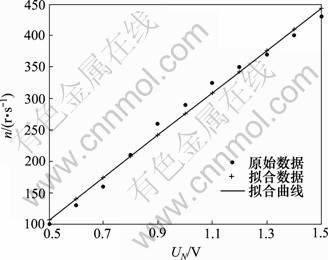
图6 电机转速与电压关系
Fig.6 Relationship between motor rotational speed and voltage
2 机器人的模糊控制
本文设计机器人的模糊控制器结构如图7所示。机器人的位姿误差由红外传感器测得,并体现为2个传感器的输出电压v1和v2,因此,可构造位姿误差为e1=v1-v2和e2=2vmax-(v1+v2),并以上述误差为0为控制目标。模糊控制器直接以e1和e2作为2个输入量,输出量为电机电压uL和uR。
机器人上2个红外传感器之间的距离为0.03 m。由上述标定结果可知:e1的变化范围为-0.2~0.2 V,e2的变化范围为0~5.4 V。输出量选取2个电机电压uL和uR,变化范围为0.5~1.5 V。设计e1的论域为{-2,-1,0,1,2},模糊集为{NM,NS,O,PS,PM}。e2的论域为{0,1,2,3,4,5,6},模糊集为{O,PS,PM,PB}。uL的论域为{0,1,2,3,4,5,6,7},模糊集为{O,PS,PM,PB}。uR的论域为{0,1,2,3,4,5,6,7},模糊集为{O,PS,PM,PB}。输入量的隶属度函数采用高斯隶属度函数,输出量O和PB采用梯形隶属度函数,PS和PM采用三角隶属度函数。
模糊控制规则库由1个5×4的矩阵共20条语句构成(见表1),其意义在于根据机器人相对于目标点的位置和姿态角调整左、右电机的驱动电压。
表1 模糊控制规则
Table 1 Fuzzy control rules uL/uR

3 仿真与分析
采用Matlab/Simulink分别对机器人趋向点光源和跟踪运动光源的运动过程进行仿真,仿真结果分别如图8和图9所示。
图8所示为点光源的位置为(1.4,0),机器人中心位于坐标原点时趋向点光源的运动过程的仿真结果。仿真的控制周期为0.2 s,仿真时间为30 s。图中曲线代表机器人中心点移动的位置。其中:图8(a)中机器人的初始正方向为y轴正方向,图8(b)中机器人的初始正方向为x轴负方向。在这2种情况下机器人跟踪效果均良好。仿真系统中模糊控制的输入e1和e2均收敛于0,模糊控制的输出uL和uR最后收敛于0.241 V。验证了该算法的准确性和有效性,说明该控制器性能良好。
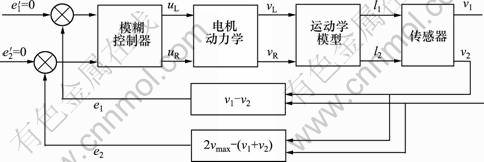
图7 机器人模糊控制系统结构
Fig.7 System structure of robot fuzzy control
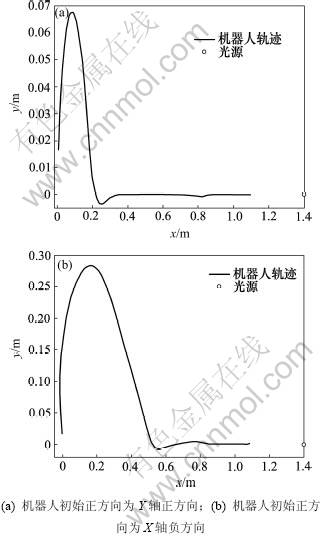
图8 趋向点光源的运动轨迹
Fig.8 Motion track of robot approaching point light source
图9所示为机器人跟踪运动光源的运动过程的仿真结果。仿真的控制周期为0.2 s,仿真时间为150 s。令机器人中心的初始位置为原点,初始方向为y轴正方向,分别进行光源沿直线和圆形轨迹运行的跟踪控制仿真。光源运动轨迹的参数方程分别为
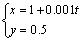 和
和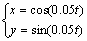 。光源沿直线和圆形
。光源沿直线和圆形
轨迹运动的仿真结果分别如图9(a)和图9(b)所示。由图9可见:跟踪效果优良。
从图8和图9可以看到:机器人的运动结束在距光源大约0.31 m处,也就是说出现了死区。出现这个问题的原因在于所使用红外传感器的测量范围有限,当红外传感器在距光源0~0.31 m的范围内时,输出电压产生饱和失真。这一问题需在下一步研究中通过控制系统硬件的优化设计来解决。
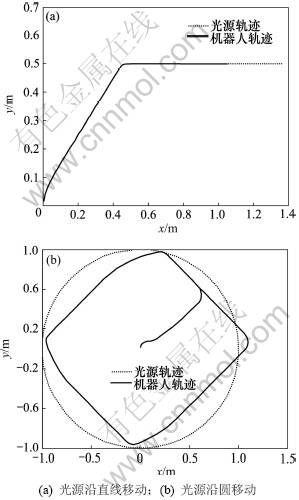
图9 跟踪运动光源的运动轨迹
Fig.9 Motion track when tracking moving light source
4 结论
本文建立了水上行走机器人的运动学模型以及执行器的动力学方程。对Water Dancer II-a型水上行走机器人的电机和红外传感器进行了分析和标定。设计模糊控制器实现了机器人对光源的跟踪,并利用Matlab/Simulink仿真水上行走机器人的运动。仿真结果验证了该算法的准确性和有效性,说明该控制器性能良好。下一步应继续研究红外传感器输出电压饱和造成的死区问题,以进一步提高自主控制系统性能。
参考文献:
[1] 吴立成, 孙富春, 袁海斌. 水上行走机器人[J]. 机器人, 2010, 32(3): 443-448.
WU Li-cheng, SUN Fu-chun, YUAN Hai-bin. Water strider robot[J]. Robot, 2010, 32(3): 443-448.
[2] Tsuchiya K, Urakubo T, Tsujita K. A motion control of a two-wheeled mobile robot[C]//IEEE International Conference on Systems, Man and Cybernetics. Tokyo, Japan, 1999: 690-696.
[3] Park K H, Cho S B, Lee Y W. Optimal tracking control of a nonholonomic mobile robot[C]//Proceedings of IEEE International Symposium on Industrial Electronics. Pusan, South Korea, 2001: 2073-2076.
[4] 黄永志, 陈卫东. 两轮移动机器人运动控制系统的设计与实现[J]. 机器人, 2004, 26(1): 40-44.
HUANG Yong-zhi, CHEN Wei-dong. Design and implementation of motion controller of two-wheeled mobile robot[J]. Robot, 2004, 26(1): 40-44.
[5] 刘磊, 向平, 王永骥, 等. 非完整约束下的轮式移动机器人轨迹跟踪[J]. 清华大学学报: 自然科学版, 2007, 47(S2): 1884-1889.
LIU Lei, XIANG Ping, WANG Yong-ji, et al. Trajectory tracking of a nonholonomic wheeled mobile robot[J]. Journal of Tsinghua University: Science & Technology, 2007, 47(S2): 1884-1889.
[6] Mitrovic S T, Durovic Z M. Fuzzy logic controller for bidirectional garaging of a differential drive mobile robot[J]. Advanced Robotics, 2010, 24(8/9): 1291-1311.
[7] Rashid R, Elamvazuthi I, Begam M, et al. Differential drive wheeled mobile robot (WMR) control using fuzzy logic techniques[C]//Asia Modelling Symposium 2010: 4th International Conference on Mathematical Modelling and Computer Simulation. Kota Kinabalu, Malaysia, 2010: 51-55.
[8] ZHANG Huai-xiang, YUAN Kui, MEI Shu-qi. Fuzzy logic cross-coupling control of wheeled mobile robots[C]//2006 IEEE International Conference on Mechatronics and Automation. Luoyang, China, 2006: 740-744.
[9] 王秀和. 永磁电机[M]. 北京: 中国电力出版社, 2007: 119-121.
WANG Xiu-he. Permanent magnet electric motor[M]. Beijing: China Electric Power Press, 2007: 119-121.
[10] 马科斯·波恩, 埃米尔·沃耳夫. 光学原理[M]. 杨葭荪, 译. 北京: 电子工业出版社, 2005: 101-105.
Max B, Emil W. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light[M]. YANG Jia-sun, transl. Beijing: Electronic Industry Press, 2005: 101-105.
(编辑 陈灿华)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:国家自然科学基金资助项目(60875062,61004023);中央民族大学自主科研计划项目(0910KYZY52);人力资源和社会保障部留学人员科技活动项目(2010年)
通信作者:王淑慧(1983-),女,河南卫辉人,博士,从事机器人、智能控制研究;电话:13466659837;E-mail: ellenwong@asee.buaa.edu.cn