DOI：10.19476/j.ysxb.1004.0609.2019.10.22
基于CFD的充填管网参数优化及输送特性
张宗国，史秀志，吝学飞
(中南大学 资源与安全工程学院，长沙 410083)
摘 要：为优化充填管网参数及研究充填料浆管道输送特性，考虑将充填倍线N、充填管径D、质量浓度c 3个影响因素进行正交设计并进行计算流体力学(CFD)试验，之后对试验结果进行极差、方差及回归拟合分析，并结合数值分析方法探讨最大流速的预测计算模型。结果表明：影响沿程阻力损失、影响最大流速的敏感性、显著性皆为D＞c＞N，且3个因素均为显著因素；得到最佳充填倍线N为3.0~4.0，质量分数c为65%~68%，充填管径D为110~120 mm，再经筛选剩下5组合适参数。研究3个因素变化对沿程阻力损失、最大流速的影响，并建立一个反映三因素下最大流速νmax的综合数学预测模型，并利用这5组对其验证，模型计算值与试验模拟值差率都在15%以下，证明预测模型有效。
关键词：充填采矿；计算流体力学；充填管网；数值分析
文章编号：1004-0609(2019)-10-2411-10 中图分类号：TD853 文献标志码：A
充填采矿法开采效率高，有效减少了岩爆等灾害，提高了采矿的安全性，因此，日益受到深井矿山的青睐[1]。将开采过程产生的废石尾砂等固体废弃物进行充填处理，也有效解决了土地占用，环境污染等问题[2]。管道输送充填料浆是其中最关键的技术之一，直接影响着充填系统的效率[3]，但随着开采深度的增加，充填管道的铺设也比以前更深、更长[4]，实现料浆的自流输送也越来越困难，因此，优化充填管网参数和研究料浆管道输送特性变得尤为重要。
充填管网布置方案中参数选取往往使用经验公式估算和环管试验得到[5-6]，但经验公式针对性不强，环管试验又价格昂贵。随着计算机技术的不断发展，基于流体力学和数值方法的计算流体动力学(CFD)已经开始用于研究充填管道的性能，为该问题的研究提供了一条新思路。查阅文献发现，利用CFD技术研究充填问题的成果主要集中在充填材料和充填流量方面，如CHEN等[4, 7]利用CFD研究了泡沫砂浆三相流以及浸出渣的管道输送特性，张修香等[8]研究不同流量下的高浓度粗骨料弯管处压力；报道中对于阻力特性的分析较多，如吴迪等[9]研究了固液两相流不同浓度、料量对沿程阻力损失的影响；WANG等[10]对深井煤矿自流输送料浆阻力损失进行了研究，ZHANG等[11]进行了粗骨料料浆管道输送阻力的研究等，但是利用CFD技术对充填管网优化中充填管径、充填倍线选取问题的研究比较少，对于充填管道最大流速的报道也很少。
基于以上分析，应用CFD技术，分析不同充填倍线(N)、质量浓度(c)以及充填管径(D)下沿程阻力损失、最大流速以及管道输送情况，并确定管道输送最佳充填管网参数，以期对实际充填管路铺设有指导意义。
1 正交试验设计及料浆参数
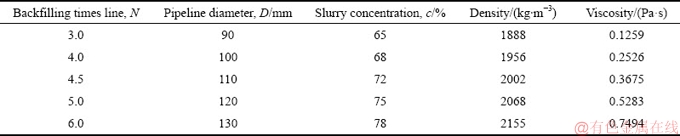
尾砂中的细颗粒有利于充填料浆保住水份，在管壁四周形成泥质圈层，对管壁进行润滑，因此在一定程度上保护了充填管[12-13]，但是细颗粒含量太高，造成需水量很大，导致充填体强度低[14]，且易使浆料在较低的质量浓度下变成膏体，不能满足高浓度的输送要求[7]，因此研究细粒级尾砂的合理浓度及其输送问题变得十分重要。以凡口铅锌矿灰砂比1:6的超细粒级分级尾砂及浸出渣为研究对象，保持充填量Qh为90 m3/h，所取的正交水平参考类似矿山常用数值范围，采用正交试验法，每个因素(N、c、D)设置5个水平，正交试验方案选择L25(53)正交表，试验设计3个因素的5个水平值及料浆参数列于表1。
表1 影响因子的水平值及料浆参数
Table 1 Parameter values of affecting factors and parameter of slurry
1.1 输送速度
料浆输送速度是影响管道输送的重要因素，速度太大，管道磨损加重[15]，速度太慢，料浆固体颗粒易在管道内发生沉降；当实际流速达到或者大于临界流速的情况下，才可以保证流体在管路中的顺利流动，可根据杜拉德公式计算充填系统所需要的临界流速[1]：
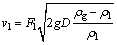(1)
式中：Fl为与充填料浆中的骨料粒径与浓度有关的系数，这里取1.2；g为重力加速度，m/s；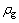
为混合料的密度，t/m2；
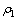为输送载体(水)的密度。
料浆在管道中的实际流速v使用下式计算：
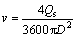(2)
式中：Qs为充填料浆的流量，取为90 m2/h；D为充填管道的实际直径，m。
计算得管径130mm的组合实际流速均小于临界流速，将这些组数据仅作为参考数据进行结果分析，优选时剔除。
2 FLUENT数值模型的建立
以表1确定的因子为基础建立相关模型，根据现场实际观察，深部的充填管道出现爆管的风险较大，现以凡口铅锌矿狮岭南深部-320 m中段至-400 m中段的充填管道为例进行分析，由于3D模型网格数目较多，采用雷诺数保持不变的原则，充填管路在实际长度的基础上缩短为实际的1/5。构建L形管充填管道输送系统，如图1所示。
2.1 几何模型参数
管道高程16 m，弯管处曲率半径为0.5 m，设置各管道参数，设置完成后，保存文件，之后利用后处理软件FLUENT进行计算。
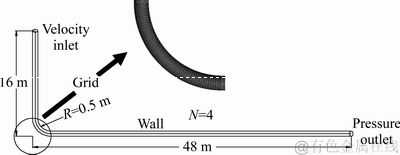
图1 充填倍线为4的L形充填管道模型
Fig. 1 L type pipeline with backfilling times line of 4
2.2 FLUENT控制方程
料浆CFD计算符合连续性及动量平衡、能量守恒，当自重应力大于沿程阻力时，料浆才可从出口流出，连续性方程、动量方程及能量方程[9]如下：
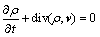(3)
式中：t为时间；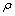
为充填料浆的密度；v为充填料浆在管道中的矢量速度；浆体是不可压缩的均质体，密度是常数，所以连续性方程就简化成：
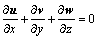(4)
式中：u、v、w为速度矢量沿x、y、z轴的3个速度的分量；
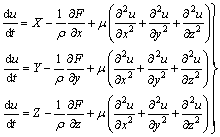(5)
式中：x、y、z为流体微元在x、y、z方向的面力；F为流体微元受到的合力；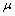
为流体的黏度。
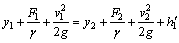(6)
式中：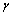
为单位体积料浆的容重；y1和y2为单位充填料浆流体的位置；F1和F2为料浆在位置y1和y2处的压力；v1和v2为流体在位置y1和y2处的速度；h1为流体从y1位置运动到y2位置过程中克服内摩擦力做的功。
2.3 FLUENT设置
计算模型的求解采用基于压力求解的方法(Pressure-based)，流体的流动特性利用雷诺数来评价，雷诺斯计算公式如下，当Re＜2300时，选择Laminar计算模型；Re＞2300时，选择计算稳定性好、精度高的k-epsilon计算模型[15]。选择压力-速度耦合求解方式为Simple。
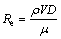(7)
式中：ρ为充填料浆密度，kg/m2；V为充填料浆流速，m/s；D为充填管路直径，m；μ为充填料浆黏度，Pa·s。
3 结果及分析
将25组试验进口压力、出口压力、沿程阻力损失及最大流速统计于表2。
3.1 方差分析
根据正交试验相关理论，运用方差分析对试验数据进行处理，得到各因素显著程度，用表3表示。其中F0.01(4,12)=5.41，F0.05(4,12)=3.26，若F＞F0.01(fj, fe)，该因素高度显著，在表中表示以**；若F0.01(fj, fe)＞F＞F0.05(fj, fe)，则因素显著，表示以*；若F＜F0.05(fj, fe)，表示该因素不显著。
3.2 敏感度分析
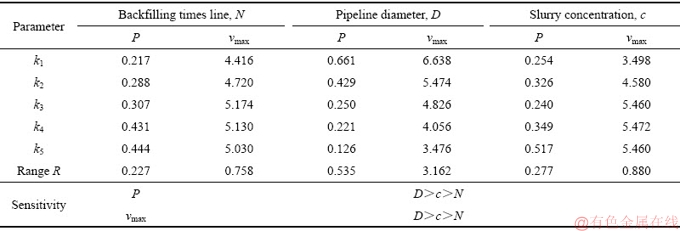
为了研究充填倍线(N)、充填管径(D)、质量浓度(c) 3个因素对沿程阻力损失P、最大流速νmax影响的敏感度，对上表中的数据进行极差分析，分析结果见表4。
显著性表明，充填管径(D)、充填倍线(N)、质量浓度(c)对沿程阻力损失、最大流速影响的影响高度显著；敏感性表明，对沿程阻力损失和最大流速皆为充填管径(D)＞质量浓度(c)＞充填倍线(N)。
表2 Fluent模拟结果表
Table.2 Fluent simulation results
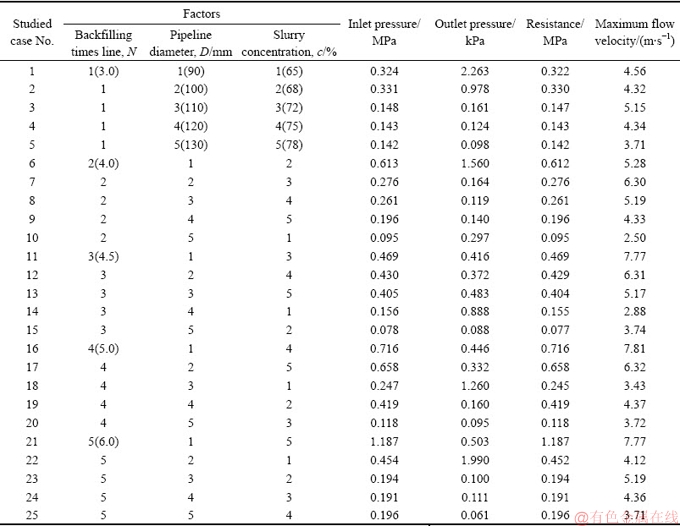
表3 沿程阻力损失P、最大流速νmax的方差分析
Table 3 Variance analysis of resistance loss P, maximum flow velocity νmax
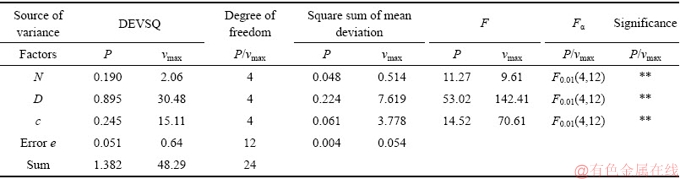
表4 极差分析表
Table 4 Range analysis
3.3 单因素分析
为分析各影响因素对充填管道输送特征的单独作用，结合表4各水平值对应的各因子的沿程阻力损失、最大流速的平均值k1-k5反映的数据，绘制各影响因素和最大流速、阻力损失间的关系如图2所示。
无量纲拟合不同影响因素与沿程阻力损失、弯管最大流速的关系如表5所列。
可以看出，各变量与P的拟合相关系数R2分别达到0.948、0.976、0.943；与νmax的拟合相相关系数R2分别为0.926、0.996、0.993，拟合效果很好。
综合图2中的曲线关系图及表5中函数关系，可以得到：
1) 充填倍线与沿程阻力损失、最大流速的关系
充填倍线N与沿程阻力损失P之间为非线性正相关，最佳充填倍线为3.0~4.0；充填倍线N与最大流速vmax之间的关系为非线性相关函数，充填倍线为4.5时，最大流速νmax达到最大，充填倍线大于4.5时，最大流速减小，但深井开采倍线过大，动力不足，充填难度增大，因此充填倍线N为3.0~4.0最佳。
2) 充填管径与沿程阻力损失、最大流速的关系
充填管径D与管道沿程阻力损失P之间为指数型减函数，增大管径能有效减小沿程阻力损失，D＜110 mm时，变化速率较大，当110 mm＜D＜130 mm时，变化速率较小，即管径增大到110mm后继续增大对降低沿程阻力损失效果不明显，D≥130 mm，发生沉降，充填管径的最优取值为110~120 mm；最大流速νmax随充填管径D与增大而减小，呈非线性减函数，充填管径的最优取值为110~120 mm。
3) 质量浓度与沿程阻力损失、最大流速的关系
管道沿程阻力损失P基本满足质量浓度c的增大而增大，当c＞72%时，变化速率明显变大，阻力增加明显，因此最优质量浓度应小于72%；质量分数c与最大流速vmax之间的关系为非线性正相关，c＞72%时，变化速率明显变小，即当质量浓度小于72%时，减小质量浓度对降低最大流速效果显著，质量分数c的最佳取值范围为65%~68%。
对上述结论进行整理分析，结果如表6所列。
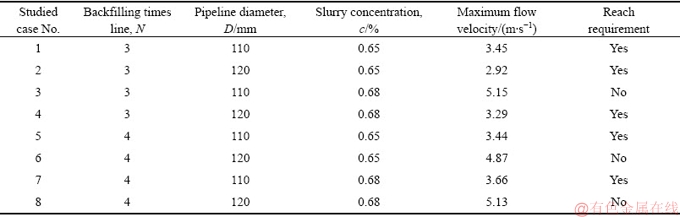
根据南非矿山充填标准：弯管处流速在满足充填要求时，最大不应超过4.0 m/s[15]，将这8个组合分别进行模拟试验，最大流速结果如表7所列。
将最大流速大于4 m/s的第3、6、8组淘汰，剩下的5组为最佳参数的组合。
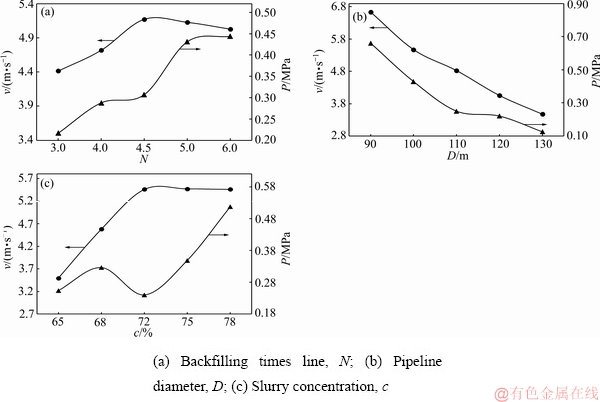
图2 各因子与最大流速、沿程阻力损失的关系
Fig. 2 Relationship between various factors and maximum flow velocity, resistance loss
表5 拟合关系表
Table 5 Equation of fitting relational
表6 不同判别因素下最优结果
Table 6 Optimal results under different discriminating factors
表7 最大流速统计表
Table 7 Statistics of maximum flow velocity
4 结果验证
凡口矿实际充填为保证较好流动性，扩散度要求不小于200 mm，文献[14]扩散度试验表明：灰砂比1:6的分级尾砂及浸出渣充填砂浆质量浓度增大，扩散度减小，当质量分数超过71%时，扩散度小于200 mm；证明模拟结论最佳质量分数65%~68%是合理的。同时，文献[1]和[8]表明在同等流量下浓度越大、充填倍线越大，阻力损失越大；且阻力损失随管径增大减小与本次模拟试验结果一致，这也验证了模拟试验的正确性。
5 最大流速νmax的数值分析和模型验证
文献[10]和[12]指出管道最大流速往往出现于弯管处，管道最大流速是造成管道磨损重要的原因之一，流速越大对管道磨损也越严重[15]，但前人在这方面的研究成果较少，基于CFD技术，综合分析3个影响因素与最大流速νmax的关系。
在表8的基础上建立预测模型：
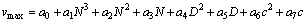(8)
式中：a0、a1、a2、…、a7分别为待求系数。
依据表3的试验数据，采用Minitab软件对最大流速ν与充填倍线N、充填管直径D、质量浓度c的预测模型进行数值分析，可得它们的关系表述为
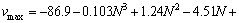
(9)
为分析所建模型的符合程度，将最大流速的方差列于表8，表中平方表示为SS；均方差表示为SM；拟合过程的确定系数表示为P；S、R-Sq、R-Sq(调整)是和拟合程度有关的数据[16]。计算得：S=0.480362，R-S q=92.3%，R-Sq(调整)=89.2%。
表8 方差分析
Table 8 Analysis of variance
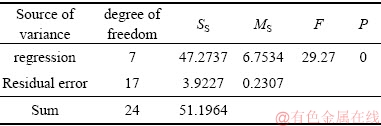
从最大流速νmax与充填倍线N、充填管直径D、质量浓度c的试验结果可以发现：
1) 相关性系数R2为92.3%，且调整的R2为89.2%，这两个值都表明最大流速νmax模型(1)与试验数据拟合效果很好；方差分析表中的P值(0)小于0.05与残差分析的P值(0.524) 大于0.05显示此回归过程拟合模型在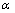
水平为 0.05 时具有显著统计意义；因此，数据回归最大流速模型成立，可用来较好地预测最大流速νmax。
2) 最大流速νmax与充填倍线N、充填管直径D、质量浓度c的数值拟合残差正态概率图可以看出残差服从正态分布如图3所示(图中A、P为Anderson-darling正态检验的平方值和确定系数)。
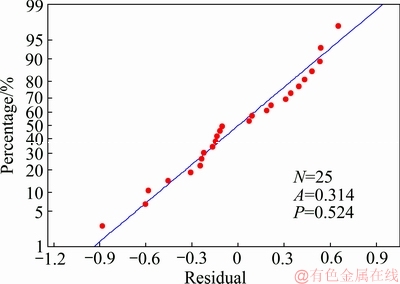
图3 预测模型残差图
Fig. 3 Residual of predictive model
使用得到的模型式(8)，对得到的最终5组合理参数的试验结果进行验证：
表9 最大流速预测表
Table 9 Predict maximum flow velocity
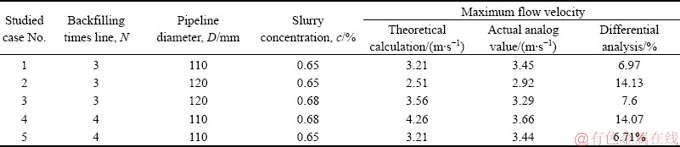
从表9中可以看出，最大流速的预测计算模型与试验模拟值相差不大，其差率都在15%以下，表明建立的预测计算模型可以用来预测最大流速。
6 实例分析
取充填倍线N为4.0，充填管径D为110 mm，质量分数c为68%的组合进行分析，通过速度云图可以发现，最大流速线由管道中心线向管道内下方向偏移，且最大流速出现在转弯处偏下位置，为3.66 m/s，按照速度超过3 m/s统计，在弯管截面内超过了的一半面积；由全压云图发现，进口处全压最大，出口处全压最小；动压变化趋势与速度基本一致，最大动压线由管道中心线向管道内下方向偏移，且最大动压同样出现在转弯处偏下位置。
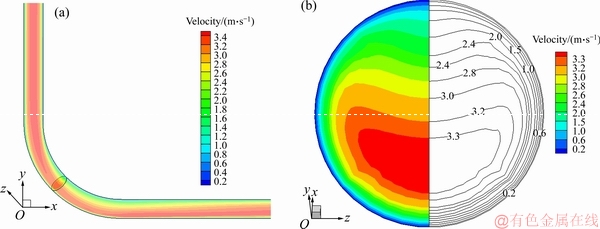
图4 全管和弯管截面速度云图
Fig. 4 Velocity cloud picture of whole pipeline(a) and cross section of elbow(b) (y=x)
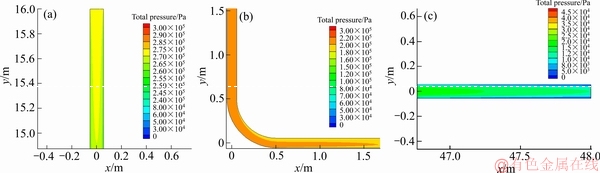
图5 入口、弯管和出口的全压云图
Fig. 5 Total pressure cloud picture of inlet(a), elbow(b) and outlet(c)
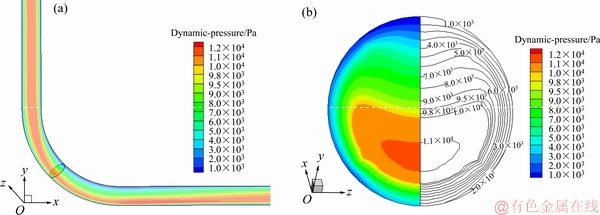
图6 全管和弯管截面动压云图
Fig. 6 Dynamic pressure cloud picture of whole pipeline(a) and cross section of elbow(b) (y=x)
7 工业实现场图
凡口铅锌矿狮岭南深部充填管道系统实际充填倍线为4，使用管径为110 mm的管道输送质量浓度为68%的充填砂浆，保证了年产150万t左右的矿量，充填管网的稳定性为矿山的高效开采提供了保障。
图7 深部充填管道弯管图
Fig.7 Elbow of deep backfilling pipeline
8 结论
1) 通过正交设计进行了25组试验，并对充填管径D、充填倍线N、质量浓度c这3个因素进行敏感性分析，结合极差分析结果得到当以沿程阻力损失P或者弯管处最大速度νmax为判别因素时，敏感性均为D＞c＞N，通过方差分析得影响因子的显著程度，结合置信区间f0.05、f0.01与F值对比，可知以沿程阻力损失P、最大流速νmax为判别因素时，三因素显著性排序皆为D＞c＞N，3个因素的影响皆高度显著。
2) 以凡口铅锌矿深部充填管道系统为基础，以灰砂比1:6的充填砂浆为研究对象，当保持充填量Qh为90 m3/h时，研究了3个因素变化对于沿程阻力损失、最大流速的影响；得到最佳的充填倍线N为3.0~4.0，质量分数c取值65%~68%，最佳充填管径D为110~ 120 mm，通过计算最大速度，最后筛选剩下5组最佳组合。
3) 以CFD模拟试验为基础，并结合数值分析方法，探讨了最大流速的预测计算模型，设计试验验证了该模型，差率都在15%以下，预测结果较好，可以用来预测最大流速，对于判断最大流速是否满足充填要求，对于充填管网参数的选取有指导意义。
4) 研究成果不仅可以对于充填管网参数优化时的最佳充填倍线、充填管径、质量浓度的选择提供理论支持，还可以对预测最大流速，预防爆管、减弱管道磨损等提供技术支持。
REFERENCES
[1] 王新民, 古德生, 张钦礼. 深井矿山充填理论与管道输送技术[M]. 长沙: 中南大学出版社, 2010: 1-3.
WANG Xin-min, GU De-sheng, ZHANG Qin-li. Theory of backfilling and pipeline transportation technology in deep mines[M]. Changsha: Central South University Press, 2010: 1-3.
[2] LU Zeng-xiang, CAI Mei-feng. Disposal methods on solid wastes from mines in transition from open-pit to under ground mining[J]. Procedia Environmental Sciences, 2012, 16: 715-721.
[3] 刘晓辉, 王国立, 赵占斌, 王少勇. 结构流充填料浆环管试验及其阻力特性研究[J]. 中国钼业, 2016, 40(5): 20-23.
LIU Xiao-hui, WANG Guo-li, ZHAO Zhan-bin, WANG Shao-yong. Study on the flow resistance characteristics of structure fluid backfilling slurry based on loop pipe testing[J]. China Molybdenum Industry, 2016, 40(5): 20-23.
[4] CHEN Xin, ZHOU Jian, CHEN Qiu-song, SHI Xiu-zhi, GOU Yong-gang. CFD Simulation of pipeline transport properties of mine tailings three-phase foam slurry backfill[J]. Minerals, 2017, 7: 149.
[5] 羊羽翔, 付建新, 宋卫东.充填管道布置方案优化中的数值模拟分析[J].黄金, 2014, 35(8): 37-40.
YANG Yu-xiang, FU Jian-xin, SONG Wei-dong. Numerical simulation in analysis of the optimization of filling pipe arrangements[J]. Gold, 2014, 35(8): 37-40.
[6] 李鹏程, 韩文亮, 田 龙. 高浓度管道输送参数计算模型的研究[J]. 金属矿山, 2005(4): 60-62.
LI Peng-cheng, HAN Wen-liang, TIAN Long. Study of model for calculating transportation parameters of pipelines with hyper concentration flow[J]. Metal Mine, 2005(4): 60-62.
[7] CHEN Xin, SHI Xiu-zhi, ZHOU Jian, CHEN Qing-song, YANG Chao. Feasibility of recycling ultrafine leaching residue by backfill: Experimental and CFD approaches[J]. Minerals, 2017, 7(4): 54.
[8] 张修香, 乔登攀. 粗骨料高浓度充填料浆的管道输送模拟及试验[J]. 中国有色金属学报, 2015, 25(1): 258-266.
ZHANG Xiu-xiang, QIAO Deng-pan. Simulation and experiment of pipeline transportation of high density filling slurry with coarse aggregates[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(1): 258-266.
[9] 吴 迪, 蔡嗣经, 杨 威, 王文潇, 王 章. 基于CFD的充填管道固液两相流输送模拟及试验[J]. 中国有色金属学报, 2012, 22(7): 2133-2140.
WU Di, CAI Si-jing, YANG Wei, WANG Wen-xiao, WANG Zhang. Simulation and experiment of backfilling pipeline transportation of solid-liquid two-phase flow based on CFD[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(7): 2133-2140.
[10] WANG Xin-min, ZHAO Jian-wen, XUE Jun-hua, YU Guo-feng. Features of pipe transportation of paste-like backfilling in deep mine[J]. Journal of Central South University of Technology, 2011, 18(5): 1413-1417.
[11] ZHANG Qin-li, CUI Ji-qiang, ZHENG Jing-jing, WANG Xin-min, WANG Xian-lai.Wear mechanism and serious wear position of casing pipe in vertical backfill drill-hole[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(11): 2503-2507.
[12] WU Ai-xiang, RUAN Zhu-en, WANG Yi-ming, YIN Sheng-hua, WANG Shao-yong, WANG Yong, WANG Jian-dong. Simulation of long-distance pipeline transportation properties of whole-tailings paste with high sliming[J]. Journal of Central South University, 2018, 25(1): 141-150.
[13] 邓代强, 高永涛, 杨耀亮, 吴顺川. 基于流体力学理论的全尾砂浆管道输送流变性能[J]. 北京科技大学学报, 2009, 31(11): 1380-1384.
DENG Dai-qiang, GAO Yong-tao, YANG Yao-liang, WU Shun-chuan. Rheological properties of full tailings slurry in pipeline transportation based on the hydromechanics theory[J]. Journal of Beijing University of Science and Technology, 2009, 31(11): 1380-1384.
[14] 杨 超, 史秀志, 周 健, 卢二伟. 超细粒级浸出渣充填配比试验研究[J]. 安全与环境学报, 2017, 17(5): 1942-1947.
YANG Chao, SHI Xiu-zhi, ZHOU Jian, LU Er-wei. Experimental study over the backfilling matching ratio of the super fine particles’ leaching residue[J]. Journal of Safety and Environment, 2017, 17(5): 1942-1947.
[15] 张钦礼, 刘 奇, 赵建文, 刘贱刚. 深井似膏体充填管道的输送特性[J]. 中国有色金属学报, 2015, 25(11): 3190-3195.
ZHANG Qin-li, LIU Qi, ZHAO Jian-wen, LIU Jian-gang. Pipeline transportation characteristics of filling paste-like slurry pipeline in deep mine[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(11): 3190-3195.
[16] 杨志全, 牛向东, 侯克鹏, 周宗红, 梁 维, 郭延辉, 程 涌, 杨八九. 砾石土层中注浆扩散参数的研究[J]. 岩土力学, 2015, 36(S1): s397-s402.
YANG Zhi-quan, NIU Xiang-dong, HOU Ke-peng, ZHOU Zong-hong, LIANG Wei, GUO Yan-hui, CHEN Yong, YANG Ba-jiu. Study of grouting diffusion parameters in gravel soil[J]. Rock and Soil Mechanics, 2015, 36(S1): s397-s402.
Parameter optimization and transportation characteristics of backfilling pipe network based on CFD
ZHANG Zong-guo, SHI Xiu-zhi, LIN Xue-fei
(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
Abstract: The orthogonal experiment and the computational fluid dynamics technology(CFD) based on three influence factors including backfilling times line(N), pipeline diameter(D), slurry concentration(c) were estimated, which was used to study the parameter optimization of backfilling pipe network and the transportation characteristics of backfilling slurry. And then, the test results of 25 groups were analyzed by the means of range, variance and regression analysis, and based on numerical analysis, the formulation was established for predicting the maximum flow velocity. The results show that the sensitivity, the significance degree ranking of the resistance loss and the maximum flow velocity all meet the relationship of D＞c＞N, all of these three factors are significant. The best proportioning scheme is the backfilling times line N of 3.0-4.0, the pipeline diameter D of 65%-68%, the slurry concentration c of 110-120 mm, after screening, the five combinations left in the end. The effects of three factors on resistance loss and maximum flow velocity were studied, and the formulation was established for predicting the maximum flow velocity. The prediction model is valid by verifying with the five groups, and the difference between the calculated values of the model and the experimental simulation values is below 15%.
Key words: filling method; computational fluid dynamics; backfilling pipe network; numerical analysis
Foundation item: Project(51874350) supported by the General Project of National Natural Science Foundation of China; Project(2017YFC0602902) supported by the National Basic Research Development Program of China; Project(41807259) supported by the National Natural Science Foundation of China
Received date: 2018-10-15; Accepted date: 2019-06-15
Corresponding author: SHI Xiu-zhi; Tel: +86-13974801752; E-mail: baopo@csu.edu.cn
(编辑 李艳红)
基金项目：国家自然科学基金资助项目(面上项目)(51874350)；国家重点研发计划资助项目(2017YFC0602902)；国家自然科学基金资助项目(41807259)
收稿日期：2018-10-15；修订日期：2019-06-15
通信作者：史秀志，教授，博士；电话：13974801752；E-mail：baopo@csu.edu.cn
