DOI: 10.11817/j.issn.1672-7207.2015.08.025

基于半监督局部保持投影的磨粒图像特征降维

张云强，张培林

(军械工程学院 七系，河北 石家庄，050003)

摘要：为有效提取磨粒图像的数字化特征，引入局部保持投影算法。针对局部保持投影在磨粒特征降维中的不足，提出一种基于Parzen窗和成对约束的半监督局部保持投影算法(PSS-LPP)。利用Parzen窗估计高维特征空间中样本的密度，然后根据各样本密度自适应调整邻域参数，并且充分利用样本的标签信息和实例约束生成成对约束集，进而指导投影权矩阵的构造，从而实现特征参数的半监督降维。将PSS-LPP应用于磨粒图像的纹理特征降维，研究结果表明：PSS-LPP对邻域参数初值和热核参数不敏感，降维性能比较稳定，磨粒识别精度明显提高。PSS-LPP可以更有效提取磨粒图像的低维特征。

关键词：磨粒分析；局部保持投影；特征提取；Parzen窗；成对约束；半监督

中图分类号：TK401.2             文献标志码：A         文章编号：1672-7207(2015)08-2937-07

Feature dimensionality reduction of wear particle images based on semi-supervised locality preserving projection

ZHANG Yunqiang, ZHANG Peilin

(Seventh Department, Ordnance Engineering College, Shijiazhuang 050003, China)

Abstract: To effectively extract digital features of wear particle images, the locality preserving projection algorithm was employed. For the disadvantages of locality preserving projection for feature dimensionality reduction of wear particles, a semi-supervised locality preserving projection algorithm(PSS-LPP) based on Parzen windows and pairwise constrains was proposed. Parzen windows were utilized to estimate the density of samples in high-dimensional feature space, and the formation of samples of labels and constrains were employed to create pairwise constrains sets which guided the construction of the projection right matrix. Then, with the projection right matrix, semi-supervised dimensionality reduction of feature parameters was implemented. PSS-LPP was applied for texture feature dimensionality reduction of wear particle images. The results indicate that PSS-LPP is not sensitive to the original value of neighborhood parameter and the kernel parameter, thus it has very stable dimensional-reduction performance. The classification accuracy is improved obviously. PSS-LPP can extract low-dimensional features of wear particle images more effectively.

Key words: wear particle analysis; locality preserving projection; feature extraction; Parzen windows; pairwise constrains; semi-supervised

基于磨粒分析的铁谱分析技术是机械设备磨损故障诊断和状态监测的重要方法之一。磨粒的形态特征复杂多样，单一的形态特征不能有效表达磨粒的形态特征。因此，许多文献从不同角度提取许多表达磨粒形态特征的特征参数。如果将所有的特征参数都用于磨粒识别，则特征参数的数量太多。无论采用何种识别方法，都会使磨粒识别过程变得复杂、计算速度极慢，甚至影响识别精度。因此，对磨粒特征进行降维是必不可少的环节。特征降维方法可分为线性和非线性两大类。线性方法中常见的有主成分分析(PCA)^[1]和线性判别分析(LDA)^[2]等。线性判别分析具有算法简单等优点，但是不能有效处理非线性可分的数据降维问题。非线性方法包括核方法和流形学习等。核方法，如核主成分分析(KPCA)^[3]，在线性降维方法的基础上，通过引入核函数的思想，虽然可以较好的解决线性降维方法在非线性问题中的不足，但是核函数的选择对数据降维结果影响很大。Isomap，LE和LLE等流形学习^[4-6]作为新的非线性降维方法，在数据降维方面与线性方法和核方法相比具有无法比拟的优势，然而这些流形学习方法不能提供显式的变换或投影矩阵，因此难以应用于模式识别。作为线性流形学习算法代表的局部保持投影算法(LPP)^[7-8]通过线性逼近LE算法，具有线性降维方法简单的优点和非线性流形学习算法较好的非线性问题处理能力，并且能够提供显式的投影矩阵，因而广泛应用于模式识别。然而，将局部保持投影LPP应用于磨粒特征降维，存在2个问题：一是磨粒样本在空间分布不均匀，全局一致的邻域参数不太合适；二是磨粒样本丰富，但是有标签样本的比例偏小，LPP不能有效区分有标签和无标签磨粒样本，无法充分利用样本标签信息和实例约束对磨粒特征进行降维。为了充分利用磨粒样本信息，提取出数量少、表达能力强的磨粒特征，本文作者设计了一种基于Parzen窗^[9]和成对约束^[10]的半监督局部保持投影算法(PSS-LPP)。

1  流行学习与局部保持投影算法

流形学习是近年来发展起来的一类重要的维数约简方法。它认为高维空间的数据存在一个潜在的低维流形上，试图将人类的认知流形规律引入机器学习领域，使机器能够从有限的样本数据中发现嵌入在高维空间中的低维流形结构，并给出有效的高维数据的低维表示。

1.1  流形学习问题描述

流形学习问题的数学描述为：假设有高维数据样本X={x₁，x₂，…，x_n}，其中x_i∈R^D为独立同分布的随机样本，散布在光滑的d维流形M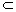R^D上，d＜＜D，M为嵌入在D维欧式空间中的d维流形，并定义嵌入映射f: M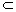R^D→R^d。流形学习就是在没有任何关于M和d的先验信息的条件下，根据有限的观测数据样本X发现未知的嵌入映射f，并且找到与高维观测数据一一对应的低维嵌入Y={y₁，y₂，…，y_n}，其中y_i∈R^d。

1.2  局部保持投影算法

局部保持投影(LPP)是一种线性的流形学习算法，本质上是对LE算法的线性逼近，它兼顾了非线性流形学习和线性降维方法的优点。LPP基于近邻图来建立数据间的映射，在保持数据局部结构特征的条件下，将高维数据X映射为低维数据Y，使得高维空间中相距较近的点在低维空间中也相距较近。LPP的目的是寻求一个转换矩阵A，通过y_i=A^Tx_i将高维空间R^D的数据映射到低维空间R^d中，实现数据的维数约简。其准则函数为

          (1)

式中：W_ij为样本x_i和x_j之间的投影权值。

经过推导，变换矩阵A可通过最小化如下目标函数来获得，即

            (2)

其中，Λ为对角矩阵，Λ_ii=；L=Λ-W为拉普拉斯矩阵，W为由元素w_ij构成的投影权矩阵。

引入约束条件YDY^T=1，则式(2)最优化问题可以转化为求解如下广义特征值问题

          (3)

令a₁，a₂，…，a_d分别为上式前d个最小非零特征值对应的特征向量，则有

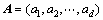            (4)

2  基于Parzen窗和成对约束的半监督局部保持投影算法

2.1  算法基本思想

设有高维数据样本X={x₁，x₂，…，x_l，x_l+1，x_l+2，…，x_l+u}，其中x_i∈R^D，前l个为有标签样本，后u个为无标签样本。PSS-LPP通过Parzen窗来估计高维空间中每个样本x_i的密度，然后根据各数据点密度自适应调整其邻域参数，并且充分利用样本的标签信息和实例约束信息构造权矩阵，最终实现数据的半监督   降维。

2.2  基于Parzen窗的邻域参数的确定

LPP选取的是全局统一的邻域参数，而磨粒图像的数据样本一般不会很理想，磨粒样本在空间分布不是均匀的，因此全局的邻域参数不太合适。局部保持投影对邻域参数ε的选取非常敏感，因此如何选择邻域参数ε非常关键。由于高维数据点之间要有一定的邻域重叠，才能使所有数据相关联，从而恢复数据的全局结构，所以ε不能太小，必须大于一定数值。但是，ε也不能取得太大，如果ε取得太大，算法会将高维空间数据中的非近邻点纳入近邻中，从而不能保证局部线性结构，得到错误的映射结果。另外，邻域参数的选择与样本在空间的分布密切相关。

Parzen窗概率密度估计是一种常用的非参数概率密度估计方法^[11]。本文利用Parzen窗估计高维空间任意数据点的密度。设有D维数据集X={x₁，x₂，…，x_n}，x_i∈R^D，对于任意x，基于Parzen窗的概率密度估计式为

         (5)

其中，n为数据样本的数目；h为窗宽；V为窗的体积；为窗函数；且满足，。

K(x,x_i)=f(x)/V称为核函数，常用的核函数有方窗、指数窗和正态窗等。本文选择效果较好的正态窗核函数，即

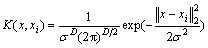     (6)

将式(6)代入式(5)可知，基于正态窗的概率密度估计式为

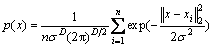     (7)

假设初始邻域参数为ε，磨粒样本x_i的ε邻域为N_ε(x_i)，近邻个数为n(x_i)，令窗宽σ=ε，定义数据点x_i的密度如下

 (8)

PSS-LPP通过如下公式自动调整每个样本的邻域参数ε(x_i)

            (9)

其中，为样本的平均密度。

由式(9)可以看出，当样本的密度比较小，即邻域数据比较稀疏时，算法会自动减少ε的数值，从而避免非近邻或者噪声作为重构数据造成错误映射；当样本的密度比较大，即邻域数据比较致密时，算法会自动增加ε的数值，避免邻域间因数据缺乏流形关联，从而引起的整体结构扭曲。因此，PSS-LPP通过分析高维空间数据样本的邻域密度，可以自适应调整邻域参数。

2.3  基于成对约束的权矩阵的构造

LPP同等对待有标签样本和无标签样本数据，不能有效利用数据的标签信息，指导数据降维。样本的先验信息通常包括类别标签和实例约束2类。试验中，获得磨粒样本的实例约束比较容易，而确定磨粒的类别比较困难。在很多情况下，我们不知道样本的具体类别标签，却知道2个样本是否属于同一个类别^[12]，因此在LPP数据降维中充分考虑样本的实例约束也非常有意义。

样本间的约束关系称为成对约束，包括正约束(Must-link)和负约束(Cannot-link)2类。设正约束集为M，负约束集为C，对于样本对(x_i，x_j)，如果属于同一类，则(x_i，x_j)∈M；反之，(x_i，x_j)∈C。正约束和负约束具有以下对称性和有限传递性^[10]。

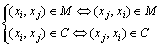         (10)

  (11)

在高维空间中，离正约束样本对最近的2个样本点，若不属于负约束集，则在低维空间中也应该是靠近的，应加入正约束集；同样，离负约束样本对最近的2个样本点，若不属于正约束集，则在低维空间中应该尽量散开，应加入负约束集。基于这种思想，PSS-LPP利用有标签样本构建初始的正约束集合M和负约束集C，然后通过以下步骤对约束集进行扩充：

Step 1  根据式(10)和(11)对成对约束进行空间传播，扩充正约束集合M和负约束集C，并记与x_i有正约束关系的样本集为M(x_i)，与x_i有负约束关系的样本集为C(x_i)；

Step 2  对任意的(x_i,x_j)∈M，分别计算样本x_i和x_j的ε邻域为N_ε(x_i)和N_ε(x_j)，基于最短路径原则扩充正约束集M，即对任意的x_l∈N_ε(x_i)，若||x_i-x_j||≥||x_l-x_j||，且M_l∩C_j=，C_l∩M_j=，则将(x_l,x_j)加入M中；同理扩充N_ε(x_j)中的点；

Step 3 对任意的(x_i,x_j)∈C，分别计算样本x_i和x_j的ε邻域为N_ε(x_i)和N_ε(x_j)，基于最短路径原则扩充负约束集C，即对任意的x_l∈N_ε(x_i)，若||x_i-x_j||≤||x_l-x_j||，且M_l∩M_j=，则将(x_l,x_j)加入C中；同理扩充N_ε(x_j)中的点；

Step 4  重复Step 1~3，直到M和C收敛。

对于样本对(x_i,x_j)，若x_j是x_i的近邻，则(x_i,x_j)属于正约束时对最小化目标函数起的作用应该大于无约束时的作用，而(x_i,x_j)属于负约束时对最小化目标函数起的作用应该小于无约束时的作用。也就是说，当(x_i,x_j)∈M时，应该增加权重W_ij；反之，则应该减小权重W_ij。因此，在完成成对约束集扩充之后，参照文献[13]，PSS-LPP通过下式构建投影权矩阵：

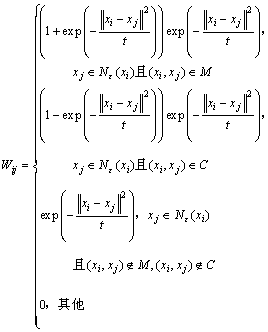 (12)

其中：t为热核参数。

2.4  半监督局部保持投影流形学习降维步骤

假设高维空间的数据样本X={x₁，x₂，…，x_l，x_l+1，x_l+2，…，x_l+u}，其中，x_i∈R^D，前l个为有标签样本，后u个为无标签样本。利用PSS-LPP对高维数据X进行降维，主要包括以下步骤：

Step 1  设置邻域参数的初始值ε和低维空间维数d；

Step 2  根据式(8)估计每个数据样本的密度，并利用式(9)自适应调整邻域参数ε(x_i)；

Step 3  利用样本的类别信息和实例约束信息构建并扩充成对约束集；

Step 4  通过式(12)计算权值W_ij，构造投影权矩阵；

Step 5  计算的前d个最小非零特征值对应的特征向量a₁，a₂，…，a_d，令A=(a₁，a₂，…，a_d)；

Step 6  通过公式y_i=A^Tx_i将高维空间R^D的数据映射到低维空间R^d中，实现数据降维。

3  实验与结果分析

3.1  常见典型磨粒与实验设计

根据实际油液监测试验，机械设备润滑油中常见的铁系磨粒可以分为球状磨粒、切削磨粒、正常滑动磨粒、严重滑动磨粒、疲劳磨粒和层状磨粒等，如图1所示。

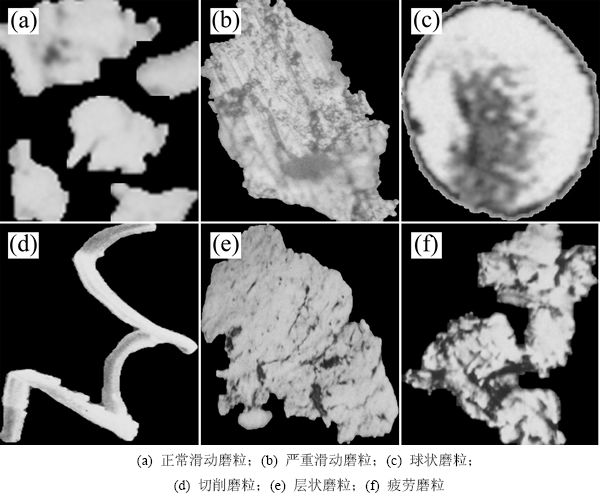
图1  典型磨粒图像

Fig. 1  Typical wear particle images

正常滑动磨粒、严重滑动磨粒、疲劳磨粒和层状磨粒是磨粒识别的难点。为验证和测试PSS-LPP的磨粒特征降维性能，以正常滑动磨粒、严重滑动磨粒、疲劳磨粒和层状磨粒为研究对象，从每类磨粒图像中先后各取40幅构成训练样本和识别样本，设计磨粒特征降维与识别实验。

实验分为2个方面。首先研究PSS-LPP算法的参数敏感性，分析邻域参数初值ε和热核参数t对算法降维性能的影响；然后，在此基础上选择最佳参数对典型磨粒进行识别，并与主成分分析(PCA)、线性判别分析(LDA)、核主成分分析(KPCA)、局部保持投影(LPP)等4种降维方法进行对比分析。

实验中通过磨粒识别成功率评价各种降维效果的好坏。研究PSS-LPP算法的参数敏感性时，采用最小二乘支持向量机(LS-SVM)^[14]分类器；在磨粒特征降维对比实验中，选择最近邻分类器、径向基神经网络^[15]和LS-SVM 3个分类器分别对磨粒进行识别。其中，LS-SVM采用“最小输出编码”策略构造多类分类器，并且核函数参数σ²和惩罚因子γ采用交叉验证的方法自动选取；神经网络的隐含层神经元个数取为42。

3.2  磨粒图像高维特征提取

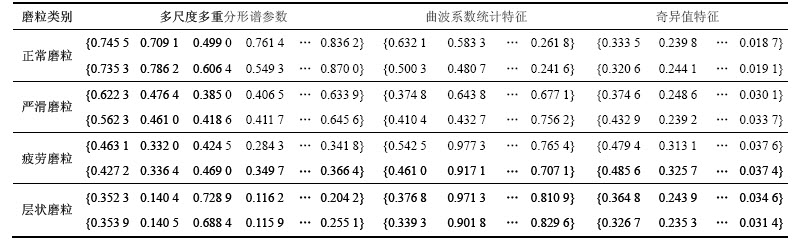
纹理特征是辨别正常滑动磨粒、严重滑动磨粒、疲劳磨粒和层状磨粒的有效特征。因此，本文提取多尺度多重分形谱参数(28个)、曲波系数统计特征(10个)和奇异值特征(21个)共59个纹理特征参数作为磨粒识别的高维特征。各参数的含义和具体提取方法在此不再赘述。表1所示为提取出的4种磨粒图像的部分纹理特征参数，其中各类参数均已作必要的归一化处理。

表1  磨粒图像高维特征

Table 1  High-dimensional features of wear particle images

3.3  邻域参数初值ε对PSS-LPP的降维性能的影响

为了分析PSS-LPP对邻域参数初值ε的敏感性，从每类磨粒图像训练样本中随机选择20幅作为有标签样本，其余20幅作为无标签样本，在固定热核参数t=10的条件下，通过改变邻域参数初值ε，研究邻域参数初值ε对PSS-LPP降维性能的影响，并与LPP算法进行对比分析。

图2所示为在不同邻域参数下，采用LPP进行特征降维后，磨粒图像识别样本的识别结果。图3所示为在不同邻域参数初值下，采用PSS-LPP进行特征降维后，磨粒图像识别样本的识别结果。

由图2可知，LPP对邻域参数十分敏感，并且选择不同的邻域参数时，识别成功率存在很大差异，随着维数的增加，识别成功率出现明显波动。由图3可知，在低维特征维数小于16时，PSS-LPP的降维性能对邻域参数初值不敏感；在低维特征维数大于16时，PSS-LPP的降维性能对邻域参数初值开始敏感，并且识别成功随着维数的增加呈现小幅波动。因此，与LPP相比，由于PSS-LPP在邻域参数选择上具有自适应性，能够根据高维空间中数据样本的密度自适应调整邻域参数，使得PSS-LPP对参数ε不敏感，降维性能比较稳定。

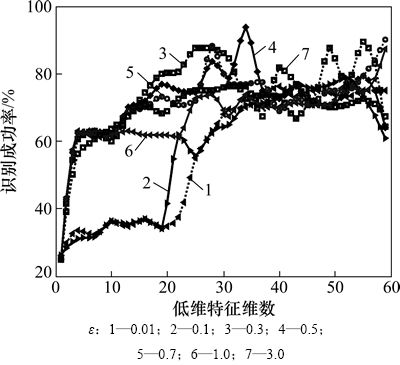
图2  不同邻域参数下LPP识别结果(t=10)

Fig. 2  Recognition results of LPP with different neighborhood parameters

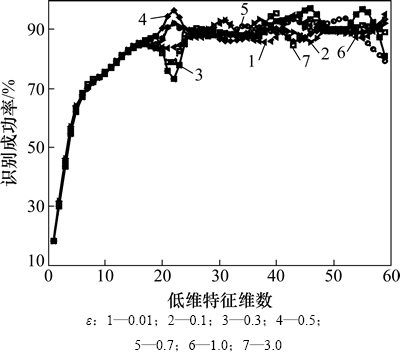
图3  不同邻域参数初值下PSS-LPP识别结果(t=10)

Fig. 3  Recognition results of PSS-LPP with different neighborhood parameters

3.4  热核参数t对PSS-LPP的降维性能影响分析

由式(12)可以看出，热核参数t对投影权矩阵W的构造有很大影响。为了分析PSS-LPP对热核参数t的敏感性，试验中仍然从每类磨粒图像训练样本中随机选择20幅作为有标签样本，其余20幅作为无标签样本，在固定邻域参数初值ε=0.5的条件下，通过改变热核参数t，研究热核参数t对PSS-LPP降维性能的影响，并与LPP算法进行对比分析。

图4和图5所示为在不同热核参数下，分别采用LPP和PSS-LPP进行特征降维后，磨粒图像识别样本的识别结果。

由图4可知，LPP对热核参数t也十分敏感，选择不同的热核参数时，识别成功率有很大差异，随着维数的增加，识别成功率呈现显著波动。由图5可知，在低维特征维数小于16时，PSS-LPP的降维性能对热核参数不敏感；在低维特征维数大于16时，PSS-LPP的降维性能对热核参数变得比较敏感，并且识别成功随着维数的增加出现小幅度波动。因此，与LPP相比，PSS-LPP的降维性能更稳定，对热核参数t不敏感。

图4  不同热核参数下LPP识别结果(ε=0.5)

Fig. 4  Recognition results of LPP with different kernel parameters

图5  不同热核参数下PSS-LPP识别结果(ε=0.5)

Fig. 5  Recognition results of PSS-LPP with different kernel parameters

3.5  基于特征降维的典型磨粒识别

为了验证PSS-LPP在典型磨粒识别中的优势，再次从每类磨粒图像训练样本中随机选择20幅作为有标签样本，其余20幅作为无标签样本，分别采用不同的降维方法和分类器对4类磨粒识别样本进行识别。

采用PCA，LDA和KPCA 3种方法对磨粒特征降维时，按照特征值的累计贡献率大于或等于98%的原则确定低维特征维数，且KPCA采用核参数σ²=1000高斯核函数。采用LLP和PSS-LPP对磨粒特征降维时，根据前面实验结果确定低维特征维数，并选择ε=0.5和t=10。最后识别实验结果如表2所示。

表2  典型磨粒识别结果

Table 2  Recognition results of typical wear particles

由表2可知：PCA降维后，特征维数最低，但是由于PCA属于线性非监督降维方法，在降维过程中没有有效利用训练样本的标签信息，导致识别正确率不是很高。LDA虽然利用了有标签样本的标签信息，但是标签样本数量有限，参与降维的训练样本不完备，所以磨粒识别效果比较差。KPCA由于引入了核函数思想，有效改善了PCA在磨粒特征非线性降维问题中的不足，从而使磨粒识别正确率显著提高，在采用最近邻分类器和径向基神经网络进行识别时，识别正确率分别达到了最大值88.8%和91.3%。LPP属于无监督流形学习降维方法，同样不能充分利用训练样本的标签信息，虽然在采用最小二乘支持向量机识别时，达到了高达93.8%的识别成功率，但是降维后的维数还有34维，维数约减效果不理想。PSS-LPP通过引入Parzen窗概率密度估计和成对约束，克服了LPP在磨粒特征降维中的不足，使得磨粒识别正确率明显提高，特别是在利用最近邻分类器和最小二乘支持向量机识别时，均获得了最好的识别效果，分别达到88.8%和96.3%。与KPCA相比，PSS-LPP虽然在采用径向基神经网络识别时的效果稍差，但是综合考虑降维后特征维数和识别成功率，PSS-LPP的降维效果优于KPCA。

因此，与其降维方法相比，PSS-LPP更能有效约简磨粒特征，从而提高磨粒的识别精度，更加适用于磨粒特征降维。

4  结论

1) 将局部保持投影算法引入磨损磨粒特征降维，针对LPP在磨粒特征降维中的不足，提出一种半监督局部保持投影算法。该算法可根据样本数据密度自适应调整邻域参数，能有效利用样本的标签信息和实例约束信息，从而实现磨粒特征半监督降维。

2) 与局部保持投影算法相比，半监督局部保持投影算法对邻域参数初值和热核参数都不敏感，具有比较稳定降维性能。

3) 半监督局部保持投影算法可有效约简磨粒特征，同时显著提高磨粒识别精度，是一种新的较好的磨粒特征降维方法。

参考文献：

[1] Roylance B J, Albidewi I A, Laghari M S. Comput-aided vision engineering (CAVE)-quantification of wear particle morphology[J]. Lubrication Engineering 1994, 50(2): 111-116.

[2] 李国宾, 孟歆, 关德林, 等. 基于小波和分形提取磨粒图像特征参数的研究[J]. 内燃机学报, 2006, 24(5): 476-479.

LI Guobin, MENG Xin, GUAN Delin, et al. Extracting feature parameter of wear particle image based on wavelet and fractal theory[J]. Transactions of CSICE, 2006, 24(5): 476-479.

[3] 吴振峰. 基于磨粒分析和信息融合的发动机磨损故障诊断技术研究[D]. 南京: 南京航空航天大学民航学院, 2001: 10-30.

WU Zhenfeng. The research of engine wear faults diagnosis based on debris analysis and data fusion[D]. Nanjing: Nanjing University of Aeronautics & Astronautics. College of Civil Aviation, 2001: 10-30.

[4] 吕植勇, 严新平, 彭雅芳, 等. 磨损磨粒的主成分聚类方法分析[J]. 摩擦学学报, 2008, 28(5): 453-456.

L Zhiyong, YAN Xinping, PENG Yafang, et al. Analysis of typical wear particles based on principal component classification[J]. Tribology, 2008, 28(5): 453-456.

[5] 王相海, 董钦科. 一种基于2D-PLDA和小波子带的虹膜识别算法[J]. 中国图象图形学报, 2011, 16(1): 59-65.

WANG Xianghai, DONG Qinke. A kind of iris recognition algorithm based on 2D-PLDA and wavelet subband[J]. Journal of Image and Graphics, 2011, 16(1): 59-65.

[6] 李岳, 温熙森, 吕克洪. 基于核主成分分析的铁谱磨粒特征提取方法研究[J]. 国防科技大学学报, 2007, 29(2): 113-116.

LI Yue, WEN Xisen, L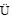 Kehong. KPCA-based technique for debris feature extraction[J]. Journal of National University of Defense Technology, 2007, 29(2): 113-116.

[7] Swung H S, Lee D D. The manifold ways of perception[J]. Science, 2000, 290: 2268-2269.

[8] Tenenbaum J B, Silva V, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290: 2319-2323.

[9] Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290: 2323-2326.

[10] 何强, 蔡洪, 韩壮伟, 等. 基于非线性流形学习的ISAR目标识别研究[J]. 电子学报, 2010, 38(3): 585-590.

HE Qiang, CAI Hong, HAN Zhuangwei, et al. ISAR target recognition based on non-linear manifold learning[J]. Acta Electronica Sinica, 2010, 38(3): 585-590.

[11] XU Yong, ZHONG Anni, YANG Jian, et al. LPP solution schemes for use with face recognition[J]. Pattern Recognition, 2010, 43(12): 4165-4176.

[12] 张学工. 模式识别[M]. 3版. 北京: 清华大学出版社, 2010: 15-20.

ZHANG Xuegong. Pattern Recognition[M]. 3rd ed. Beijing: Tsinghua University Press, 2010: 15-20.

[13] 潘俊, 孔繁胜, 王瑞琴. 加权成对约束投影半监督聚类[J]. 浙江大学学报(工学版), 2011, 45(5): 934-940.

PAN Jun, KONG Fansheng, WANG Ruiqin. Semi-supervised clustering with weighted pairwise constraints projection[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(5): 934-940.

[14] 李春芳, 刘连忠, 陆震. 基于数据场的概率神经网络算法[J]. 电子学报, 2011, 39(8): 1739-1745.

LI Chunfang, LIU Lianzhong, LU Zhen. Probabilistic neural network based on data field[J]. Acta Electronica Sinica, 2011, 39(8): 1739-1745.

[15] 陈诗国, 张道强. 半监督降维方法的实验比较[J]. 软件学报, 2011, 22(1): 28-43.

CHEN Shiguo, ZHANG Daoqiang. Experimental comparisons of semi-supervised dimensional reduction methods[J]. Journal of Software, 2011, 22(1): 28-43.

[16] ZHAO Haitao, SUN Shaoyuan, JING Zhongliang, et al. Local structure based supervised feature extraction[J]. Pattern Recognition, 2006, 39(2): 1546-1550.

[17] 钟新辉, 李少如, 费逸伟, 等. 基于支持向量机的磨粒识别[J]. 数学的实践与认识, 2008, 38(5): 54-57.

ZHONG Xinhui, LI Shaoru, FEI Yiwei, et al. Debris recognition based on support vector machine[J]. Mathematics in Practice and Theory, 2008, 38(5): 54-57.

[18] 王伟华, 殷勇辉, 王成焘. 基于径向基函数神经网络的磨粒识别系统[J]. 摩擦学学报, 2003, 23(4): 340-343.

WANG Weihua, YIN Yonghui, WANG Chengtao. Wear debris recognition system based on radius basis function network[J]. Tribology, 2003, 23(4): 340-343.

(编辑  赵俊)

收稿日期：2014-08-10；修回日期：2014-10-25

基金项目(Foundation item)：国家自然科学基金资助项目(50705097)；清华大学摩擦学国家重点实验室开放基金资助项目(SKLTKF09B06)(Project (50705097) supported by the National Natural Science Foundation of China; Project (SKLTKF09B06) supported by the Fund of State Key Laboratory of Tribology Science)

通信作者：张云强，博士研究生，从事信号、模式识别与机械故障诊断研究；E-mail：zhangyunqiangoec@163.com