主动偏航过程兆瓦级风机偏航系统失稳振动特性

李晓光^{1, 2}，赵萍²，韩德海²

(1. 中南大学 机电工程学院，湖南 长沙，410083；

2. 南车株洲电力机车研究所有限公司，湖南 株洲，412001)

摘要：根据兆瓦级风机偏航系统主动偏航原理，建立兆瓦级风机偏航系统振动模型，并在引入摩擦失稳阻尼比的基础上对主动偏航过程兆瓦级风机偏航系统摩擦失稳进行仿真研究和实验验证。研究结果表明：过大的预紧力矩和过大的静摩擦因数是导致偏航系统产生失稳振动现象的主要因素，而较合理的静摩擦因数和预紧力矩可有效避免主动偏航过程兆瓦级风机偏航系统摩擦失稳现象发生。

关键词：兆瓦级风力发电机组；主动偏航；运动学特性；摩擦；失稳振动

中图分类号：TH138.51             文献标志码：A         文章编号：1672-7207(2013)03-0949-06

Characteristics of unstable vibration for megawatt wind power yaw system in process of active yaw

LI Xiaoguang^{1, 2}, ZHAO Ping², HAN Dehai²

(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;

2. Zhuzhou Electric Locomotive Research Institute Co. Ltd., Zhuzhou 412001, China)

Abstract: According to the active yaw theory of a megawatt-class draught fan, a vibration model of the yaw system of megawatt-class draught fan was built and simulation analysis and experiments on the yaw system friction instability generating in the course of active yaw were conducted based on the damping ratio of friction instability. The results show that over preloaded torque and static friction coefficient mainly cause the instability vibration phenomenon of the yaw system, and a reasonable value of preloaded torque and static friction coefficient can avoid the phenomenon effectively occurring in the active yaw course.

Key words: megawatt wind power; active yaw; kinematic characteristics; friction; unstable vibration

风能是一种取之不尽、用之不竭的绿色可再生能源^[1-2]。对于近年来发展主流的兆瓦级风机，其偏航系统可确保风机的风轮始终处于迎风状态，从而可在较大程度上充分利用风能，提高风机发电效率。但在兆瓦级风机偏航系统中，由偏航滑动轴承与偏航驱动构成典型的低速伺服运动系统具有内部参数变化、外加负载干扰、传动系统中的摩擦干扰和模型的不确定性以及非线性等特点^[3-4]，其偏航动作具有转速低、承载大、摩擦制动的典型特征，因此，兆瓦级风机偏航系统在主动偏航过程中不可避免地会出现振动幅值和噪声大幅度增加现象，不但导致兆瓦级风机偏航系统主动偏航运动的均匀性差，而且容易产生冲击，从而最终在很大程度上影响兆瓦级风机偏航控制系统的精度^[5-9]。对于兆瓦级风机偏航系统主动偏航运动振动问题，国内外许多学者就影响兆瓦级风机偏航系统振动机理和影响因素进行了研究，并取得了许多成果^[10-14]，但如何采取有效手段探明兆瓦级风机偏航系统主动偏航运动振动产生的诱因和机理仍然是主动偏航过程兆瓦级风机偏航系统性能提高的瓶颈。为此，本文作者针对兆瓦级风机偏航系统主动偏航运动振动现象，从运动学和摩擦学角度研究偏航系统的运动学机理，建立合适的兆瓦级风机偏航系统振动模型和运动学方程，研究分析偏航系统的主动偏航运动规律和影响因素，以便对防止主动偏航过程兆瓦级风机偏航系统失稳振动设计提供参考。

1  主动偏航过程兆瓦级风机偏航系统振动数学模型

1.1  主动偏航过程兆瓦级风机偏航系统振动机理

将偏航系统模拟为支承在扭转弹簧刚度为S和扭振阻尼d之上的质量为m、转动惯量为I以及半径为R的圆盘，如图1所示。偏航电机作用在圆盘的力为F，产生的力矩M=R×F，使圆盘发生转动。同时，主动偏航过程偏航系统和偏航齿圈之间存在摩擦力，产生摩擦力矩M_f，如图2所示。其中偏航系统的转动方向始终为偏航方向，因此，偏航系统的转动方向主要取决于偏航角度θ。

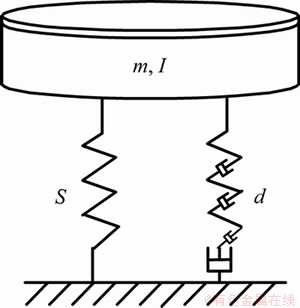
图1  偏航系统振动模型

Fig.1  Vibration model of yaw system

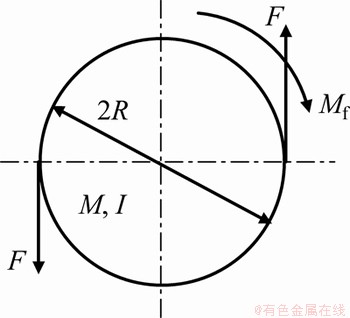
图2  主动偏航过程偏航系统受力分析

Fig.2  Stress analysis of yaw system in process of active yaw

1.2  主动偏航过程兆瓦级风机偏航系统平衡位置振动

只有在偏航力矩M=R×F等于或大于摩擦力矩M_f时，偏航系统才会开始转动，其偏航转动运动方程可表示为

I·(d²θ/dt²)+d·(dθ/dt)+S·θ=M-M_f         (1)

偏航力矩M=R×F刚刚克服静摩擦力矩M_f0时的位置为平衡点dθ(0)/dt=0，则在该平衡点有：

M=M_f0                   (2)

任意时刻的摩擦力矩M_f为

M_f=M_f0-△M_f(dθ/dt)            (3)

式中：△M_f(dθ/dt)为偏航力矩减量(N·m)，与偏航系统旋转角速度dθ/dt有关，且△M_f(dθ/dt)≥0。

将式(3)代入式(1)可得：

I·(d²θ/dt²)+d·(dθ/dt)+S·θ=△M_f(dθ/dt)       (4)

在平衡点附近，摩擦力矩减量可近似表示为

△M_f(dθ/dt)=K△_M(0)·(dθ/dt)          (5)

式中：K_△M(0)为△M_f在原点的斜率。

将式(5)代入式(4)，可将有黏性阻尼的强迫振动方程简化为有黏性阻尼的自由振动方程：

I·(d²θ/dt²)+d·(dθ/dt)+S·θ=K_△M(0)·(dθ/dt)     (6)

对式(6)进行整理，可得偏航系统偏航转动运动方程：

I·(d²θ/dt²)+[d-K_△M(0)]·(dθ/dt)+S·θ=0       (7)

由微分方程解的理论，对于作为弱阻尼的偏航系统来说，式(7)的通解可表示为

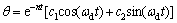        (8)

式中：ω_d²=ω_n²-n²；n=0.5[d-K_△M(0)]/I；ω_n为偏航系统固有频率，ω_n=(S/I)^0.5；c₁和c₂为待定常数，可由初始条件确定。

分别对式(8)求时间t的一次导数和二次导数，可得偏航系统的角速度方程和角加速度方程分别为：

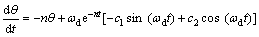   (9)

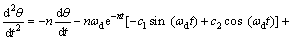
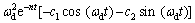       (10)

根据主动偏航过程兆瓦级风机偏航系统平衡位置振动的实际情况，当t=0时，有dθ/dt=0，(d²θ/dt²)= K_△M(0)/(R·I)，则待定常数c₁和c₂分别为：

c₁= K_△M(0)/(R·I·ω_n)            (11)

c₂=nK_△M(0)/(R·I·ω_n·ω_d))          (12)

因此，式(7)的终解为

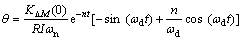   (13)

1.3  主动偏航过程兆瓦级风机偏航系统摩擦失稳分析

由式(7)可知：当有效阻尼系数d-K_△M(0)＜0即K_△M(0)>d时，出现负阻尼现象，主动偏航过程兆瓦级风机偏航系统将发生摩擦失稳现象。

将式(7)变形为有黏性阻尼的自由振动方程的通用形式：

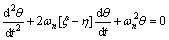        (14)

式中：ξ为主动偏航过程兆瓦级风机偏航系统转动阻尼比，ξ=d/[(2(I·S)^0.5]，ξ≈0.02~0.06；η为主动偏航过程兆瓦级风机偏航系统转动摩擦失稳阻尼比，η=K_△M(0)/[(2(I·S) ^0.5]。

偏航系统与偏航齿圈上表面的静摩擦力矩M_f01可表示为

M_f01=μR(mg+150T_s/d_m)           (15)

式中：m为偏航系统质量(kg)；g为当地重力加速度(m/s²)；T_s为单个螺栓的预紧力矩(N·m)；d_m为预紧螺栓的标称直径(m)。

偏航系统与偏航齿圈下表面的静摩擦力矩M_f022可表示为

M_f02=μR(150T_s/d_m)             (16)

因此，主动偏航过程兆瓦级风机偏航系统总静摩擦力矩M_f0为

M_f0= M_f01 + M_f02              (17)

假设摩擦力矩减量K_ΔM(0)与总静摩擦力矩满足关系：

K_ΔM(0)=α·M_f0               (18)

式中：α为摩擦力矩减量变化率，一般为40%~80%。

已知某兆瓦级风机偏航系统的相关参数如下：转动惯量I=114 492.1 kg·m²，刚度S=0.33×10⁹ N·m/rad，旋转半径R=1.157 5 m，静摩擦因数μ=0.05，预紧螺栓M33的性能等级为10.9，偏航系统总质量为60.5 t。利用这些参数对主动偏航过程兆瓦级风机偏航系统进行仿真，研究分析不同预紧力矩T_s下摩擦失稳阻尼比η以及静摩擦因数μ和预紧力矩T_s与摩擦失稳阻尼比η关系，结果分别如图3和图4所示。

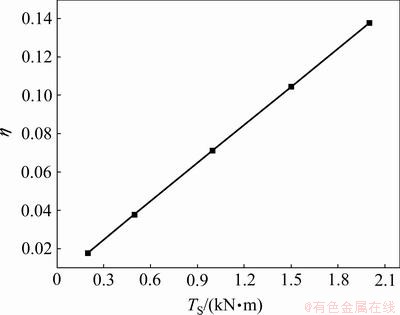
图3  预紧力矩T_S与摩擦失稳阻尼比η的关系

Fig.3  Relationship between tightening torque damping and ratio of friction instability

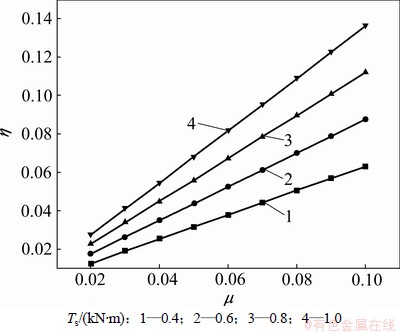
图4  静摩擦因素μ和预紧力矩T_S与摩擦失稳阻尼比η的关系

Fig.4  Relationship among static friction coefficient, tightening torque damping and ratio of friction instability

由图3可见：随着预紧力矩T_s的逐渐增加，摩擦失稳阻尼比η呈线性增加；当预紧力矩T_s增加到0.9 kN·m左右时，摩擦失稳阻尼比η＞0.06，主动偏航过程兆瓦级风机偏航系统摩擦失稳开始发生。其主要原因为：预紧力矩T_s增大导致摩擦面间正压力增大，即相当于增大了偏航系统的质量，对于刚度一定的偏航系统，其质量增加则意味着刚性减弱，最终导致偏航系统摩擦失稳现象发生。

由图4可见：随着静摩擦因数μ和预紧力矩T_s逐渐增大，摩擦失稳阻尼比η呈线性增加，并且其增长幅度越来越大；当预紧力矩T_s=0.4 kN·m，静摩擦因数μ=0.10时，偏航系统摩擦失稳阻尼比η＞0.06，主动偏航过程兆瓦级风机偏航系统摩擦失稳开始发生；而当预紧力矩T_s=1 kN·m，静摩擦因数μ=0.04时，导致偏航系统摩擦失稳阻尼比η＞0.06。因此，在确保预紧力矩T_s尽量满足偏航系统正常工作情况下，必须采取较好措施使静摩擦因素保持在恰当的范围内，才能有效避免主动偏航过程兆瓦级风机偏航系统摩擦失稳现象的发生。

当静摩擦因数μ=0.07，预紧力矩T_s=0.6 kN·m时，主动偏航过程兆瓦级风机偏航系统振动曲线如图5所示。显然，此时主动偏航过程兆瓦级风机偏航系统已经产生摩擦失稳振动现象。

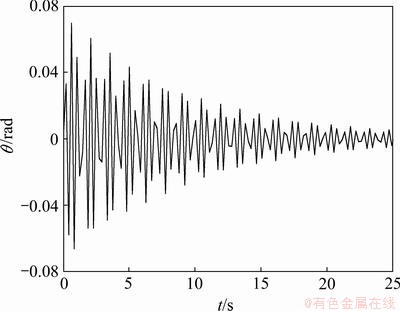
图5  主动偏航过程兆瓦级风机偏航系统振动曲线

Fig.5  Vibration curve of yaw system in megawatt wind power in process of active yaw

2  主动偏航过程兆瓦级风机偏航系统振动实验验证

2.1  实验设备性能参数

用于主动偏航过程兆瓦级风机偏航系统振动实验验证的实验设备主要参数如表1所示，加速度传感器型号为PCB加速度传感器(333B30)。

2.2  传感器布置

根据风机偏航结构，结合所关注的振动位置和振动方向，选择合理的加速度传感器的布置点(4个位置)。传感器主要布置在横向吊架上，具体位置如图6所示(1号和3号传感器可测量偏航系统的扭转振动，2号和4号传感器可测量偏航系统的径向振动)。

2.3  实验数据及结果分析

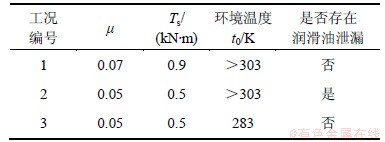
主动偏航过程兆瓦级风机偏航系统偏航振动测试工况如表2所示。在工况1和工况2所示的测试过程中，环境温度较高(＞303 K)，同时，工况2中存在润滑油泄漏现象。在工况3所示的测试过程中，环境温度t₀较低(283 K)，且不存在润滑油泄漏现象。

表1  LMS振动测试系统指标

Table 1  Indices of LMS vibration testing system

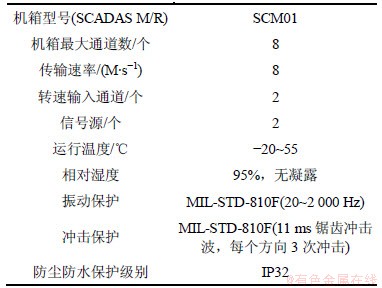
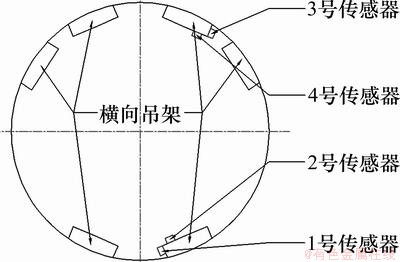
图6  传感器布置简图

Fig.6  Diagram of sensor arrangement

表2  主动偏航过程兆瓦级风机偏航系统振动测试工况

Table 2  Vibration testing condition of yaw system in megawatt wind power in process of active yaw

主动偏航过程兆瓦级风机偏航系统偏航振动测试所得到的振动加速度时域信号图和频谱图分别如图7和图8所示。

从图7和图8可以看出：在工况1和工况2中，主动偏航过程兆瓦级风机偏航系统发生了较明显的颤振，1~4号传感器测得的振动信号的基频范围为45~55 Hz，其振动幅值为0.02~0.20 m/s²，比工况3中振动幅值大1个数量级，其振动较为剧烈；而工况3中主动偏航过程兆瓦级风机偏航系统发生颤振不明显，其振动频谱幅值为0.002~0.020 m/s²，说明偏航系统整体在各个方向上的振动强度没有明显的差别，偏航过程处于较稳定状态。

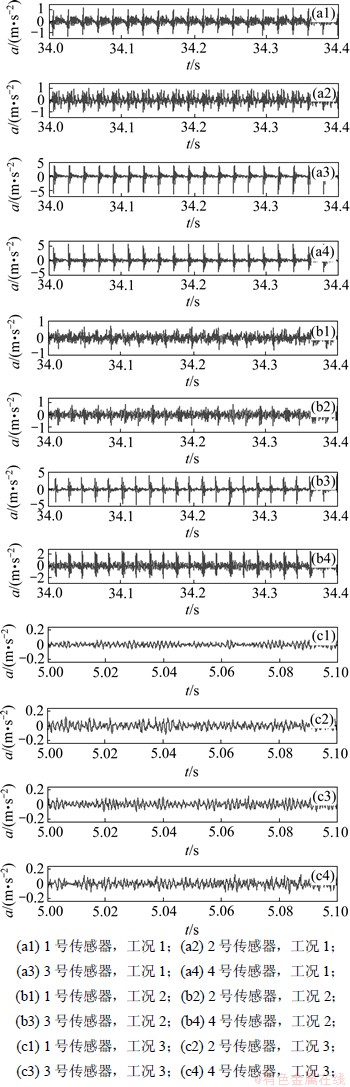
图7  振动加速度a的时域信号图

Fig.7  Charts of time domain signal for vibration acceleration

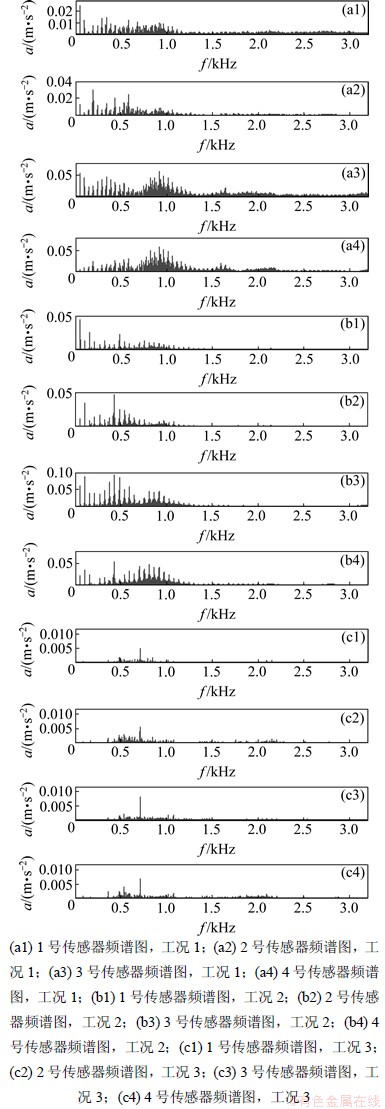
图8  振动加速度a的频谱图

Fig.8  Charts of frequency spectra for vibration acceleration

与工况3相比，尽管工况2所示的测试过程中只是环境温度t₀较高并存在润滑油泄漏等情况，但由于润滑油泄漏和环境温度升高，其综合作用使得静摩擦因数有较大幅度增大，最终导致摩擦失稳阻尼比η增长幅度较大，从而导致主动偏航过程中兆瓦级风机偏航系统摩擦失稳现象发生。

3  结论

(1) 建立了兆瓦级风机偏航系统振动模型和运动学方程，并引入摩擦失稳阻尼比，得出了主动偏航过程兆瓦级风机偏航系统摩擦失稳条件。

(2) 过大的预紧力矩和过大的静摩擦因素是导致偏航系统产生失稳振动现象的主要因素。

(3) 在确保预紧力矩T_s尽量满足偏航系统正常工作的情况下，必须采取较好措施，使静摩擦因数和预紧力矩保持在恰当的范围内，才能有效避免主动偏航过程兆瓦级风机偏航系统摩擦失稳现象发生。

参考文献：

[1] Saidur R, Rahim N A, Islam M R, et al. Environmental impact of wind energy[J]. Renewable and Sustainable Energy Reviews, 2011, 15(5): 2423-2430.

[2] Peter T. Wind power as a clean-energy contributor[J]. Energy Policy, 2008, 36(12): 4397-4400.

[3] 鄂加强, 张彬, 董江东, 等. 新型风电偏航减速机动力学仿真分析[J]. 中南大学学报: 自然科学版, 2011, 42(8): 2324-2331.

E Jiaqiang, ZHANG Bin, DONG Jiangdong, et al. Dynamics simulation and analysis on new wind power yaw reducer[J]. Journal of Central South University: Science and Technology, 2011, 42(8): 2324-2331.

[4] 鄂加强, 李光明, 张彬, 等. 兆瓦级风电偏航减速机行星齿轮疲劳仿真分析[J]. 湖南大学学报: 自然科学版, 2011, 38(9): 32-38.

E Jiaqiang, LI Guangming, ZHANG Bin, et al. Fatigue simulation and analysis on planetary gear of megawatt wind power yaw reducer[J]. Journal of Hunan University: Science and Technology, 2011, 38(9): 32-38.

[5] ZHU Chenghui, LI Pengju, WANG Jianping, et al. Research on intelligent controller of wind-power yaw based on modulation of artificial neuro-endocrine-immunity system[J]. Procedia Engineering, 2011, 15: 903-907.

[6] WU Zhi, WANG Hengsheng. Research on active yaw mechanism of small wind turbines[J]. Energy Procedia, 2012, 16(A): 53-57.

[7] Canale M, Fagiano L, Milanese M, et al. Robust vehicle yaw control using an active differential and IMC techniques[J]. Control Engineering Practice, 2007, 15(8): 923-941.

[8] Nagai M, Shino M, Gao F. Study on integrated control of active front steer angle and direct yaw moment[J]. JSAE Review, 2002, 23(3): 309-315.

[9] Yang P, Takamura T, Takahashi S, et al. Development of high-precision micro-coordinate measuring machine: Multi-probe measurement system for measuring yaw and straightness motion error of XY linear stage[J]. Precision Engineering, 2011, 35(3): 424-430.

[10] WANG Fengtao, ZHANG Liang, SONG Lutao, et al. Order tracking of wind power gearbox vibration signal based on SVD noise reduction and IFE[J]. Energy Procedia, 2011, 13: 7147-7156.

[11] Kusiak A, ZHANG Zijun. Control of wind turbine power and vibration with a data-driven approach[J]. Renewable Energy, 2012, 43: 73-82.

[12] Schmid J, Drapalik M, Kancsar E, et al. A study of power quality loss in PV modules caused by wind induced vibration located in Vienna[J]. Solar Energy, 2011, 85(7): 1530-1536.

[13] Yasui H, Marukawa H, Momomura Y, et al. Analytical study on wind-induced vibration of power transmission towers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 83(1/2/3): 431-441.

[14] 廖明夫, 黄巍, 董礼, 等. 风力机偏航引起的失稳振动[J]. 太阳能学报, 2009, 30(4): 488-492.

LIAO Mingfu, HUANG Wei, DONG Li, et al. Unstable torsional vibration of wind turbines caused by nacelle yawing[J]. Acta Energiae Solarls Sinica, 2009, 30(4): 488-492.

(编辑  陈灿华)

收稿日期：2012-04-02；修回日期：2012-07-20

基金项目：国家高技术研究发展计划(“863”计划)项目(2008AA05Z410)

通信作者：李晓光(1965-)，男，江西萍乡人，博士研究生，教授级高级工程师，从事复杂机电系统性能仿真与优化研究；电话：0731-28445280；E-mail: lixg@teg.cn