障碍物条件下智能车辆换道路径规划的近优解

李玮¹，段建民¹，龚建伟²

(1. 北京工业大学 电子信息与控制工程学院，北京，100124；

2. 北京理工大学 智能车辆研究所，北京，100081)

摘要：以智能车辆换道过程为研究对象，结合多项式理论和动态RBF神经网络，提出1种车辆换道路径规划方法，得到在一定边界条件下智能车辆换道路径的近优解。该方法首先利用矩形包裹换道车辆及障碍车辆并对其进行碰撞检测，然后利用动态RBF神经网络生成合理的车辆换道边界条件，最后在边界条件以及性能指标函数的约束下，根据多项式理论得到以时间为参数的换道路径近优解。其中动态RBF神经网络具备在线学习能力，能够利用具有优良性能指标的边界条件实现自更新。计算机仿真验证了该方法的正确性及有效性，尤其是在复杂路面情况下体现了该换道路径规划算法的优势。

关键词：车辆换道；路径规划；近优解；多项式；神经网络

中图分类号：U491          文献标志码：A         文章编号：1672-7207(2011)S1-0505-07

Near-optimal solutions to lane change path planning for an intelligent vehicle in presence of moving obstacles

LI Wei¹, DUAN Jian-min¹, GONG Jian-wei²

(1. College of Electronic Information and Control Engineering, Beijing University of Technology, Beijing 100124, China;

2. Intelligent Vehicle Research Center, Beijing Institute of Technology, Beijing 100081, China)

Abstract: Based on polynomial theory and radial basis function (RBF) neural network, a path planning method for the intelligent vehicles lane changing process was proposed. The near-optimal solutions of the lane changing path in the fixed boundary conditions can be obtained by this method. In this method the lane changing vehicle and obstacle vehicles were presented by rectangle, and then in the constraints of collision detect conditions, boundary conditions and comfort performance index that the near-optimal solutions of the lane changing path were calculated. In addition, the dynamic RBF neural network was used to solve the problem that how to select a reasonable boundary conditions. By this dynamic RBF neural network the reasonable boundary conditions were calculated and the neural network has the function of online learning, which was optimized by itself. Simulation results prove the correctness and feasibility of this algorithm, and illustrative examples show the advantage of this new method in the case of lane changing with multiple obstacles.

Key words: vehicles lane change; path planning; near-optimal solutions; polynomials; neural network

车道变换是车辆行驶过程中最常见的运动之一，随着智能车辆技术研究的逐渐深入，车辆换道行为已经成为国内外学者研究的热点，而换道路径的生成是实现车道变换的前提条件，其性能指标决定了在车道变换过程中车辆能否通畅、快速和安全的运行，因此，对换道路径规划算法的深入研究对于提高道路通行能力、减少车辆延误、改善道路拥挤有着重要意义。

目前关于换道路径的规划问题已有大量的研究成果。Lin等^[1-2]利用场方法进行了车辆路径规划的研究；Gomez^[3]采用β样条曲线生成具有连续曲率的车辆行驶路径；在此基础上李玮等^[4]通过控制点的选择优化了B样条曲线所生成换道路径的性能指标；考虑到车辆在行驶过程中需要满足乘坐舒适性要求，Shimizu等^[5]提出1种回旋曲线路径规划方法以减小规划路径所产生的最大侧向加速度；Yang等^[6-7]利用Bezier曲线进行路径规划，并在1辆电动汽车上现了避障功能；Qu和游峰等^[8-10]分别利用多项式理论给出了车型机器人与车辆换道路径的规划方法，并且Qu还进一步给出了路径的近优解析解。以上提到的规划方法虽然能够在一定程度上满足预期目标，但都在不同方面存在着缺陷，如利用场方法进行路径规划通常需要将车辆看作成一个质点，这与实际情况不相符合，因此，不能直接应用于具有运动学限制的车辆系统。目前虽然有研究通过对其生成的路径增加约束条件来解决这一问题，但这极大地增加了运算量。利用样条曲线和Bezier等曲线进行路径规划其难点在于控制点的选择，如何使控制点作用下的路径满足车辆运动学限制和舒适性要求并能够对障碍物进行碰撞检测，目前尚没有较好的解决方法。采用多项式进行路径规划的关键为边界条件的设定，一组合适的边界条件能够使规划得到的路径具有合理性，反之生成的路径则很难达到设计要求。

本文作者在现有的研究成果基础上提出1种基于多项式与动态RBF神经网络的智能车辆换道路径规划方法，并得到障碍物条件下换道路径的近优解。该方法首先根据不同的外部环境利用RBF神经网络计算得到换道车辆的边界条件，然后结合多项式理论利用得到的边界条件进行换道路径的规划，从而得到满足碰撞检测条件的换道路径数族；最后通过引入乘坐舒适性能指标函数得到在该边界条件下所生成换道路径的近优解。

1  问题阐述

图1所示为障碍物条件下车辆换道过程。其中x-y为车体坐标系，X-Y为世界坐标系；C₀为换道车辆，O₁为障碍车辆，O₁位于C₀的前方并与之相同车道。整个换道过程为C₀车由初始车道按照一定的换道路径经过一定时间运动到目标车道。完成换道动作需要在初始状态与目标状态之间寻找1条光滑曲线使换道车辆C₀在整个换道过程中既能够保证与障碍O₁不发生碰撞，同时还能够满足车上乘客的乘坐舒适性要求。

图1  障碍物条件下车辆换道过程

Fig.1  Vehicles lane changing process in obstacle condition

2  基于多项式的换道路径规划方法

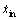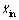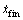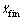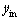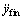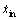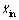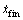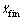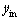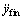采用多项式方法进行换道路径规划。首先定义换道车辆C₀的边界条件X′=[x_in,,, x_fin,,]^T，Y′=[ y_in,,, y_fin,,]^T与t_in和t_fin。其中x_in，和分别表示换道初始时刻C₀在世界坐标系下沿X方向的位置、速度和加速度；x_fin，和分别表示换道完成时刻C₀在世界坐标系下沿X方向的位置、速度和加速度；y_in，和分别表示换道初始时刻C₀在世界坐标系下沿Y方向的位置、速度和加速度信息；y_fin，和分别表示换道完成时刻C₀在世界坐标系下沿Y方向的位置、速度和加速度信息；t_in表示换道过程的起始时刻，t_fin表示换道过程的完成时刻。考虑车辆在实际换道过程中X方向速度的变化要比Y方向的大，其调整的自由度更大，因此，在X方向与Y方向分别选取6次与5次多项式来构造换道路径函数。定义时间参数矩阵：

(1)

构造换道路径函数：

X(t)=a₆t⁶+a₅t⁵+a₄t⁴+a₃t³+a₂t²+a₁t+a₀       (2)

Y(t)=b₅t⁵+b₄t⁴+b₃t³+b₂t²+b₁t+b₀          (3)

此时只要给定1组边界条件X′，Y′，t_in与t_fin便可以通过求解齐次线性方程(4)唯一确定1条Y方向上的换道路径。

Y(t)=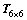B^T                 (4)

其中：B=[ b ₅, b ₄, b ₃, b₂, b₁, b₀]为换道路径参数。由于X方向换道路径是时间的6次函数，仅仅通过以上的边界条件无法求得唯一确定的换道路径X(t)，为此将假设a₆为已知，将其固定，此时根据边界条件以及时间参数矩阵便可以通过式(5)唯一的确定特定a₆条件下X方向换道路径X(t)。

X(t)-a₆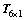=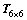A^T              (5)

其中：=[ t_in⁶, 6t_in⁵, 30t_in⁶, t_fin⁶, 6t_fin⁵, 30t_fin⁶]；A=[a₅, a₄, a ₃, a ₂, a ₁, a ₀]。通过式(5)可以看出：在一定边界条件下通过对a₆进行遍历便可以得到1组与之对应的X方向换道路径。至此，寻找1条合适换道路径的问题转化成寻找1个合适a₆的问题。接下来给出a₆选取的具体方法。

首先，给定换道过程的边界条件并按照经验确定1个a₆的大致范围，在该范围内以一定的步长对a₆进行遍历，并根据每1个a₆计算出其对应的换道路径；接下来，对生成的这些换道路径与车道中存在的障碍物进行碰撞检测，从而得到不与障碍物发生碰撞条件下的a₆的取值范围；最后引入乘坐舒适性指标函数在a₆的取值范围内寻找1个近优值从而确定a₆的取值。由于a₆值是按照一定的步长进行遍历的，所以，此时得到的a₆不是1个最优值，而是1个近优值。

前面已经给出了换道路径的计算方法，下面以图1中的工况为例讨论碰撞检测问题。

考虑到车辆在平面上的垂直投影为1个近似矩形，所以采用与车辆形状最为接近的矩形对换道车辆与障碍车辆进行包裹。

如图2所示，定义换道车辆C₀垂直投影的长度与宽度分别为和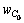；障碍车辆O₁垂直投影的长度与宽度分别为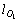和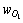；C₀的重心距离车辆的前边沿与后边沿的距离分别为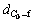和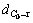；O₁的重心距离车辆的前边沿与后边沿的距离分别为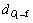和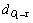；C₀车与O₁车X方向重心间的距离为L；O₁车沿X方向行驶，速度为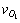。对2辆车的4个角点按照逆时针分别进行标记，其中虚线表示C₀在换道过程中的中间状态。

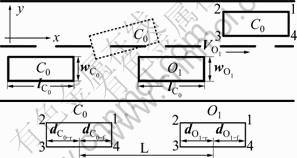
图2  换道过程

Fig.2  Lane changing process

图3所示为C₀车在图1所示换道过程中的1个中间状态，其中L_Sd为1条过O₁车第2角点并与C₀车3和4角点所在直线相平行的直线，d_d为这2条直线的垂直距离。d_v为C₀车第3角点到O₁车1和2角点对应侧边的垂直距离。接下来对换道车辆C₀与障碍车 辆O₁进行碰撞检测。考虑到图2中所示的换道过程  是C₀车由初始车道行驶到与之相邻的前进方向左侧车道，在这个过程中最有可能发生碰撞的模式为如下3种：(1) C₀车的第4角点与O₁车的2-3边发生碰撞；(2) C₀车的3-4边与O₁车的第2角点发生碰撞；(3) C₀车的第3角点与O₁车的1-2边发生碰撞。从理论上  来说还有可能出现另外4种碰撞形式，但当边界条件中y_fin＞0时，Y(t)始终为单调递增，与这4种碰撞形势不相符，因此不必考虑。

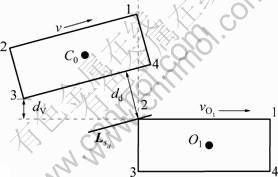
图3  碰撞检测

Fig.3  Collision detection

对以上3种碰撞模式进行碰撞检测。碰撞检测分2个阶段：第1阶段从C₀车第4角点的X方向坐标等于O₁车第2角点的X方向坐标时刻开始；到C₀车第3角点的X方向坐标等于O₁车第2角点的X方向坐标时刻结束。在这个阶段内2辆车不发生碰撞的条件是d_d≥0，d_d=0表示C₀车与O₁车处于临界碰撞状态。第2阶段从第1阶段结束时刻开始到换道完成时刻结束。在该阶段中需要保证C₀车第3角点的Y方向坐标始终位于O₁车1、2角点所在直线的上方，即d_v≥0，其中等号成立为临界碰撞状态。

按照上面提到的碰撞检测步骤便可以确定图1所示工况下的a₆值取值范围(此时a₆的取值范围为1个开区间)。实际中d_d=0与d_v=0的情况是不可取的，因为在换道过程中C₀车与O₁车需要保持一定的安全距离，所以，将碰撞检测条件改为：

d_d≥θ₁   d_v≥θ₂                (6)

其中：θ₁与θ₂为两个大于0的正实数。当得到a₆的取值范围之后需要从中选择一个最优的值来作为X方向换道路径函数的系数，为此引入性能指标函数。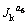

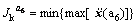           (7)

该性能函数的含义为：在a₆取值范围内所生成的1族X方向换道路径中具有最小加速度极值路径所对应的a₆。实质上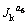，是车辆换道过程中关于乘客乘坐舒适性的一个指标函数，一般而言，为了满足乘坐舒适性的需要将车辆的最大X方向及Y方向加速度限制在±2 m/s²以内。至此，根据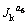函数便可以得到换道路径参数a₆值的近优解。由于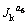函数是按照一定的步长在a₆的取值范围内对其进行遍历的，因此，得到的a₆为近优解而非最优解。

3  边界条件的选取

边界条件的选取对于所生成换道路径的性能指标影响非常重要，一组好的边界条件能够使生成的换道路径具有较好的侧向加速度变化曲线；相反，一组不合理的边界条件很可能使生成的换道路径不能够满足乘坐舒适性指标，同时生成的换道路径与实际驾驶过程不相符，如图4所示。

图4是以图2工况为例，采用多项式方法计算得到的1组X方向上的加速度变化曲线，共有3条，分别对应着不同的边界条件。从图4可见：第1条加速度变化曲线最大值超过了3 m/s²，不满足乘坐舒适性要求，并且在换道过程中出现了X方向的负加速度，这与实际驾驶过程不相符合；第2条曲线的加速度极值在满足舒适性指标的范围之内，但其变化趋势仍然不够平缓；相对于前2条加速度曲线，第3条是最好的，首先它的X方向加速度极值最小，并且变化幅度平缓，因此，其对应的边界条件在这1组里面是最优的。

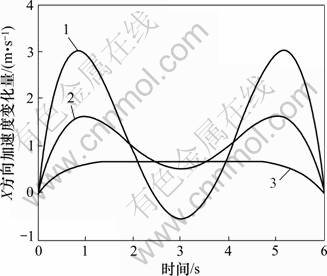
图4  X方向加速度变化曲线

Fig.4  Acceleration in X direction

通过这个例子可以看出边界条件合理选取的重要性，但目前尚未有文献给出如何获取具有较好性能指标边界条件的有效方法，针对这一现状本文作者提出1种基于动态RBF神经网络的边界条件生成算法来解决该问题。径向基函数(Radial basis function，RBF)神经网络由于其具有简单的拓扑结构和强大的非线性映射及全局逼近能力，在模式识别、函数逼近、系统的建模和辨识等方面得到了广泛的应用。接下来以图2所示的工况为例，建立动态RBF神经网络来生成换道所需的边界条件。

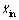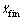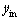首先根据实际需要设定t_fin的取值。以直线换道为例，边界条件中，x_in，，，y_in，，，与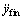的取值均为0，y_fin一般取为车道宽度，假设2辆车之间的距离L以及O₁车速度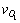可通过仪器测量得到，因此在设定好t_fin的前提下所需要确定的边界条件只有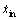，x_fin与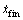，而已知条件为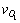，L和t_fin。根据以上条件设定RBF神经网络的输入节点数目为3，输出节点的数目为3。

RBF神经网络应用的关键是其结构设计问题，隐含层节点数和相应数据中心的确定是网络设计的难点。常规RBF神经网络需要在学习前输入数据的中心个数，因此，不能用于动态输入模式的在线学习算法。为此，在网络结构设计中本文作者采用动态RBF神经网络，具体为：首先利用最近邻聚类算法中心进行初步选择，然后利用K-均值聚类对最近邻聚类算法的选择结果进行进一步的调整，并在此基础上进一步调整中心点，从而在一定程度上弥补了最近邻聚类算法的不足。以上设计过程可参见文献[11]。该网络能够根据实际系统需要增加或删除神经网络隐含层的节点，因此，不需要事先确定隐节点的数目，其具体个数可以根据样本的增加自适应地调整，使神经网络具有良好的自适应能力，从而解决了RBF神经网络结构过大或过小的问题。

图5所示为采用动态RBF神经网络生成边界条件的整体流程图，其中“动态RBF神经网络”事先根据经验数据训练完成。生成边界条件的具体流程为：首先根据已知条件经过RBF网络得到边界条件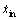，x_fin与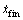，然后引入换道路径性能指标函数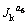对其进行评估，达到合格及以上标准的边界条件可以用于车辆的实际

换道，若性能指标达到优良水平则将该组边界条件加入到样本库中对其进行更新，同时在线对动态RBF神经网络重新进行训练。最后，若性能指标达不到合格标准，则结束路径规划同时取消车辆的换道操作。

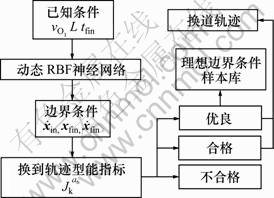
图5  系统框图

Fig.5  System frame

4  数值仿真

以一复杂工况为例进行计算机仿真来验证所提出的换道路径规划方法的可行性及有效性。

图6所示的是1个具有多重障碍物条件下的换道路径规划，换道车辆C₀需要在障碍车辆O₁与O₂之间寻找到1条合适的换道路径。在保证换道过程中不与障碍车辆发生碰撞的前提下，还要具有一定的安全余量。所提出的路径规划方法对这类复杂工况同样有 效，表1中给出了车辆参数、障碍车辆速度、安全距离和换道时间等一系列信息，通过RBF神经网络得到边界条件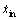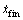，与x_fin分别为：15.5 m/s，18.3 m/s和109.5 m。图7所示为在该边界条件下生成换道路径的参数曲线。

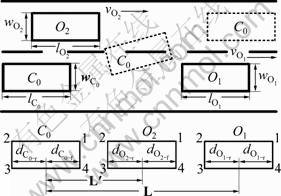
图6  复杂换道过程

Fig.6  Complicated lane changing process

表1  换道参数

Fig.1  Parameters for lane changing process

图7(a)所示是在参数a₆取值范围之内所生成换道路径的最大X方向加速度变化曲线。由图7(a)可见：在a₆的取值范围内，当a₆=-0.000 4时，其对应的换道路径具有最小X方向加速度极值。图7(b)所示是换道车辆X方向速度的变化曲线，由于边界条件选取较为理想，因此该过程是一个平稳加速过程。图7(c)所示是换道路径所产生的X方向加速度变化曲线，可见该曲线变化平稳，未有负向加速度值产生，这与实际换道过程完全相符，并且将加速度极值控制在一个较小范围内，能够较好地满足乘坐舒适性需要。图7(d)所示为生成路径的曲率变化曲线。仿真结果表明：本文作者提出的路径规划方法得到的换道路径在满足安全性条件的前提下具有较好的性能指标，能够较好地满足乘坐舒适性要求。

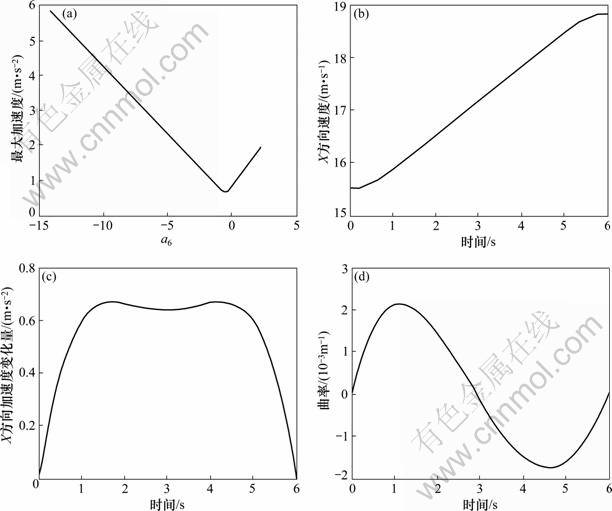
图7  仿真结果

Fig.7  Simulation results

5  结论

 (1) 提出1种智能车辆换道路径规划方法，并得到了在一定外部条件下换道路径的近优解。该方法利用多项式作为换道路径的基函数，将换道车辆及障碍车辆用与之形状最为切合的矩形进行包裹，并进行碰撞检测；在碰撞检测的过程中将寻找具有一定安全距离的换道路径族的问题转化为确定X方向多项式参数a₆值范围的问题，从而简化了问题处理的难度。

(2) 利用动态RBF神经网络解决了多项式路径规划算法的边界条件选取问题，根据不同的外部状况通过动态RBF神经网络生成合理的边界条件。

(3) 采用所提出的路径规划方法得到的换道路径在满足安全性条件下其有较好的性能指标，能够较好地满足乘坐舒适性要求。

参考文献：

[1] Lin C L, Li Y H, Aouf N. Potential-field-based evolutionary route planner for the control of multiple unmanned aerial vehicles[J]. Journal of Aerospace Engineering, 2010, 224(11): 1229-1242.

[2] Shimoda S, Kuroda Y, Iagnemma K. High-speed navigation of unmanned ground vehicles on uneven terrain using potential fields[J]. Robotica, 2007, 25(4): 409-424.

[3] Gomez B F, Cuesta F, Ollero A, et al. Continuous curvature path generation based on β-spline curves for parking manoeuvres[J]. Robotics and Autonomous Systems, 2008, 56(4): 360-372.

[4] 李玮, 高德芝, 段建民. 智能车辆自由换道模型研究[J]. 公路交通科技, 2010, 27(2): 119-123.
LI Wei, GAO De-zhi, DUAN Jian-ming. Research on lane change model for intelligent vehicles[J]. Journal of Highway and Transportation Research and Development, 2010, 27(2): 119-123.

[5] Shimizu M, Kobuyashi K, Watanabe K. Clothoidal curve-based path generation for an autonomous mobile robot[C]//Proceedings of the 2006 SICE-ICASE International Joint Conference, Busan: 2006: 478-481.

[6] Yang K, Sukkarieh S. Real-time continuous curvature path planning of UAVs in cluttered environments[C]//Proceeding of the 5th International Symposium on Mechatronics and its Applications, Amman, Jordan, 2008.

[7] Long H H, Yashiro H, Nejad H, et al. Bézier curve based path planning for autonomous vehicle in urban environment[C]// Proceeding of the 2010 IEEE Intelligent Vehicles Symposium, San Diego: 2010: 1036-1042.

[8] Yang J, Qu Z H, Wang J, et al. Comparison of optimal solutions to real-time path planning for a mobile vehicle[J]. IEEE Transactions on Systems, Man, and Cybernetics Part A: Systems and Humans, 2010, 40(4): 721-731.

[9] Qu Z H, Wang J, Plaisted C E. A new analytical solution to mobile robot trajectory generation in the presence of moving obstacles[J]. IEEE Transactions on Robotics, 2004, 20(6): 978-993.

[10] 游峰, 王荣本, 张荣辉. 智能车辆换道与超车轨迹跟踪控制[J]. 农业机械学报, 2008, 39(6): 42-45.
YOU Feng, WANG Rong-ben, ZHANG Rong-hui, et al. Lane changing and overtaking control method for intelligent vehicle based on backstepping algorithm[J]. Nongye Jixie Xuebao/Transactions of the Chinese Society of Agricultural Machinery, 2008, 39(6): 42-45.

[11] 李明河, 王萌, 施艳艳. 基于动态径向基函数神经网络的多变量解耦控制[J]. 浙江大学学报: 工学版, 2007, 41(10): 1701-1705.
LI Ming-he, WANG Meng, SHI Yan-yan. Multivariable decoupling control based on dynamic radial basis function neural network[J]. Zhejiang Daxue Xuebao (Gongxue Ban)/Journal of Zhejiang University: Engineering Science, 2007, 41(10): 1701-1705.

(编辑 何运斌)

收稿日期：2011-04-15；修回日期：2011-06-15

基金项目：国家自然科学基金重点资助项目(90920304)；先进制造技术北京市重点实验室开放项目(0010005466015)

通信作者：李玮(1982-)，男，河北廊坊人，博士研究生，从事智能车辆网络智能控制的研究；电话：15101648706；E-mail: liwei727@126.com