DOI： 10.11817/j.issn.1672-7207.2020.08.027
矿井风网与采空区流场边界耦合模型与求解技术
吴奉亮1, 2,高亚超1, 2,常心坦1, 2
（1. 西安科技大学 安全科学与工程学院，陕西 西安，710054；
2. 西安科技大学 西部矿井开采与灾害防治教育部重点实验室，陕西 西安，710054）
摘要:为揭示煤矿巷道和采空区中整体风流的流动机理，通过将采空区漏风边界的流量添加到矿井通风网络，建立矿井风网与采空区流场的边界耦合模型。基于矿井通风网络的节点压力解算法与采空区渗流场的有限元求解法，研究矿井风网与采空区流场边界耦合模型的迭代求解流程。分析基于线性渗流模型求解采空区非线性渗流模型的方法及控制方程组，用PARDISO作为耦合模型中大型稀疏线性方程组的求解器的软件开发接口。采用VC++与ObjectARX编写相应的模拟软件(简称i-MVS)模拟2个算例，验证模型的有效性与性能。研究结果表明：采空区流场的模拟需要矿井通风网络的解算结果为其提供压力边界条件，对新的矿井通风网络的解算又需要采空区流场的模拟结果来提供漏风边界上的流量，两者之间形成了相互依赖的耦合关系；耦合模型中的新风网是一个含有边界流量的不闭合网络，必须采用矿井通风网络的结点压力法进行解算；耦合模型实现了矿井通风网络与多个采空区流场的集成求解，其计算量是常规采空区流场模拟的若干倍，采用PARDISO求解器实现了对耦合模型的高效求解；相比于常用的模拟煤矿采空区流场的方法，耦合模型的准确度提高了12%。
关键词:矿井通风网络；采空区流场；有限元方法；节点压力法；耦合；PARDISO
中图分类号:TD725 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207（2020）08-2333-10
Boundary coupling model and solution technology of mine ventilation network and gob flow field
WU Fengliang1, 2, GAO Yachao1, 2, CHANG Xintan1, 2
(1. College of Safety Science and Engineering, Xi’an University of Science and Technology, Xi’an 710054, China；
2. Key Laboratory of Western Mine Exploitation and Hazard Prevention, Ministry of Education, Xi’an University of Science and Technology, Xi’an 710054, China)
Abstract: To describe the mechanism of the airflows in the airways and gob areas of underground coal mine, the boundary coupling model of mine ventilation network and gob flow field was established by adding the flux of the air leaked into gob to mine ventilation network. Based on the node pressure method for mine ventilation network and the finite element method for gob seepage field, an iterative solution process for the boundary coupling model of mine ventilation network and gob flow field was studied. The method of solving the nonlinear seepage model of dob and the related equations were analyzed based on the linear seepage model. The programming interface of PARDISO was studied to solve the large sparse linear system in the coupling model. A computer program of i-MVS was developed to implement the coupling model in VC++ and ObjectARX. Two illustrative examples were created to verify the validity and performance of the coupling model. The results show that the simulation of gob flow field needs the solution of mine ventilation network to provide pressure boundary conditions, and the solution of the new mine ventilation network needs the simulation results of gob flow field to provide the flow on the leakage boundary, which forms a mutually dependent coupling relationship. The new ventilation network in the coupling model is an unclosed network with boundary air flow of gob and can only be solved by the node pressure method of mine ventilation network. In the coupling model, the gob flow field is simulated with the ventilation network simultaneously resulting in its amount of calculation being several times of that of the common gob flow field simulation. The solver of PARDISO is efficient in solving the coupling model and the accuracy of coupling model is improved by 12% compared with that of the previous method.
Key words: mine ventilation network; gob flow field; finite element method; node pressure method; coupling; PARDISO
通风不仅为井下矿工提供足够新鲜空气，而且是防控井下各种污染、爆炸和窒息性气体的基本措施。对于煤矿，供给采煤工作面的风流会连续漏入采空区，这种难以避免的漏风极易引发采空区遗煤自燃及瓦斯爆炸。我国采煤工作面40%~60%的瓦斯来自采空区漏风，超过60%的煤矿火灾来自于采空区遗煤自燃[1-2]；美国煤矿广泛采用大量风流流经采空区的Bleeder形式通风系统[3]。可见，掌握采空区中因漏风形成的危险区域对防控煤矿爆炸与火灾事故具有重要的作用。由于矿井通风系统的复杂性，难以直接观测采空区流场，数值模拟成为国内外学者研究这2个部分井下风流的主要手段。矿井通风系统(包括风道、风机和控风设施等元素)常被描述成1个一维的网络模型，风流在其中的流动遵循节点流量平衡和回路风压平衡定律，描述该定律的非线性方程组以井巷的风量或节点的压力作为未知数，未知数的数量常超过1 000个。长期以来，研究者围绕此非线性方程组提出了牛顿法、斯拷特-恒斯雷法等多种不同解算方法[4-5]，许多由行业研究者自主开发的具有良好可视化[6]和并行计算[7]能力的解算软件已被广泛用于理解与控制这种复杂的通风系统。与巷道中风流的一维网络模型不同，采空区中的风流主要采用二维或三维场模型来描述，在计算流体力学CFD(computational fluid dynamics)技术支撑下，大量模拟研究很好地展现了风流在采空区这个不可见区域中的流动过程及其可能引发问题的危险区域，如模拟采空区流场[8-9]、判定采空区中煤自燃危险区域[1-2,10]、模拟采空区煤自燃[11-13]和瓦斯运移过程[1-2]。但现有模型多是将采空区与矿井通风网络分离，没有考虑漏风对采空区边界条件的影响。采空区流场将随着边界条件的改变而改变，通风系统的改变也将导致预先定义的边界条件失效，因此，整体求解井下巷道与采空区中的风流流动是一件十分有意义的工作。人们一直在尝试建立矿井风网与采空区流场的统一求解模型。文献[14-15]将采空区划分成许多纵横交错的分支，与矿井风网形成一个整体。但与目前采空区模拟使用的主流技术CFD相比，这种方法不严密。近年已有学者尝试将网络解算模型添加到商业CFD软件中[16]，或将CFD算法移置到网络解算软件中[17]，这些工作在一定程度上显示了通风网络与采空区流场集成求解的优越性，但还没有很好地考虑两者的耦合关系。本文利用矿井风网与采空区流场的边界流量来建立两者的耦合模型，并研究模型的求解方法。
1 矿井风网与采空区流场的边界耦合模型
1.1 整体模型
采空区中的风流在冒落煤岩体中的流动是各向同性非均匀介质渗流，由于采空区宽度与深度远大于高度，三维采空区流场完全可简化为如图1所示的平面流场。矿井通风网络解算需要在井巷系统之上建立风网结构，采用有限元求解采空区流场则需要将求解区域划分成单元。以图1所示典型的U形工作面通风系统为例，高度简化矿井风网，可以建立图2所示的几何模型，该模型同时包含矿井风网与采空区流场。
图1 U形工作面通风系统
Fig. 1 Layout of working face with U-ventilation system
图2中节点③～⑥是风网的边界节点，节点⑦～⑩是采空区的边界节点；边界流量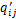
表示风网边界节点i与采空区边界单元j之间的风流交换量。对于采空区(老空区)的漏风密闭与风网之间的边界也可建立类似的虚拟分支，因此，当引入足够多的边界节点与虚拟分支时，常规模型中分离的风网与采空区流场在边界上耦合成一个整体。采空区边界节点压力可通过风网边界节点计算，即图2中的节点⑦可取节点③的压力，节点⑧的压力为节点③和④的压力平均值。矿井风网与采空区流场的边界耦合模型将基于采空区流场及风网的求解方法来研究如何求得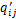，以及如何将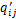反馈到风网解算模型中。
图2 矿井风网与采空区流场边界耦合模型示意图
Fig. 2 Schematic diagram of boundary coupling model between ventilation network and gob flow field
1.2 边界耦合模型及解耦流程
由于很难导出关于图2中所有节点压力或流量流速为未知数的控制方程组，采用分离计算的办法求解整体模型。新风网(图2中风网与边界)的节点流量平衡方程将与常规通风网络不同，此处应为
(1)
式中：N为风网节点数；qij为连接结点i和j的风网分支的流量，m3/s，由i和j节点的压力来计算：
(2)
式中：Rij为连接结点i和j的分支的风阻，kg/m7；pi和pj分别为节点i和j的压力，Pa。式(1)左侧是连接节点i的所有分支的流量之和，右侧为来自采空区的流量。对于普通的通风网络，即图2中的风网部分，式(1)右侧恒等于0。将式(2)代入式(1)得到的方程组以风网节点压力为未知数，因此，解此方程组来求解通风网络的方法称为节点压力法。
式(1)中加入边界流量qik'，一方面，导致新风网不再是封闭的，另一方面，在网络解算与采空区流场模拟之间形成了相互依赖的耦合关系：采空区流场的模拟依赖于对新网络的解算为其提供边界上的节点压力；同时新网络解算，即式(1)中的边界流量qik'又依赖于采空区流场模拟结果来确定。尽管2个部分看似仅在边界上耦合，但求解过程不得不涉及完整的风网及整个采空区。
图3所示为风网与采空区流场的迭代解耦流程。图3中Qgk为第k次迭代中求得的所有边界单元的边界流量qik'构成的向量；D为Qgk与Qgk-1之差的元素的绝对值的最大值，当D小于给定精度ε时，求得风网与采空区流场耦合模型的解。因此，从分离求解来看，图2整体模型也是一个风网与采空区流场之间的耦合模型。
需要指出的是：1) 新网络的不封闭性导致无法使用常规的回路风量法进行求解，对此本文采用风网结点压力法[18]来解决；2) 当多个采空区按图2所示方式连接到风网中时，图3所示求解流程仍然有效，由于矿井风网表示了所有井巷的风路，以上用1个采空区为例的推导过程，实则建立了风网与多采空区流场的边界耦合模型及求解流程。自编程研究采空区漏风流场，需要解算大型线型方程组，当多个采空区连接到风网时，解方程的计算量是普通采空区流场模拟计算量的若干倍。
图3 风网与采空区流场边界耦合模型的迭代求解流程
Fig. 3 Iteration flow between ventilation network calculation and gob flow field simulation
2 有限元法求解采空区流场的控制方程组
采空区流场的控制方程组是指以采空区所有待求结点压力为未知数的代数方程组。若将风流在采空区中的流动先假设为线性渗流，则图1采空区流场的定解数学模型为下列的微分方程：
(3)
式中：P为采空区中的压力函数，Pa；K为渗流系数，m/s；G为整个采空区区域；p0为L1上的已知压力；nx和ny分别为边界外法线上单位向量在x和y方向的分量。将图2中三角形单元的3个节点按逆时针方向依次编号为i，j和k，相应压力分别记为pi，pj和pk。记L1边界上的节点(压力已知)数为w，不在L1边界上的采空区节点(压力待求)数为s；按待求在前、已知在后的顺序将所有采空区节点压力向量记为Pg=(Pu，Pb)，其中，待求压力列向量Pu=(p1，p2，…，ps)T，已知压力列向量Pb=(ps+1，…，ps+w)T。基于有限元理论中的变分法或加权余量法均可导出关于Pg为未知数的控制方程组[19]：
(4)
式中：M称为总体矩阵，可由每个单元的单元矩阵Ae合成。Ae是对称矩阵
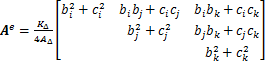(5)
AΔ为单元面积，m2；KΔ为单元渗透系数；系数b和c由三角形单元的i，j和k这3个节点的坐标x和y决定，对应关系分别是：bi=yj-yk，ci=xk-xj，bj=yk-yi，cj=xi-xk，bk=yi-yj，ck=xj-xi。设mi，mj和mk分别表示单元的i，j和k节点的压力在Pg向量中的序号，则Ae的1，2和3行或列分别与M的mi，mj和mk行或列对应，合成是指单元矩阵元素累加到总体矩阵中。显然，式(4)中Pg的元素只有前s个是未知数，因此，不用计算M的每一个元素。M具有图4所示的分块特点，即M的前s行、s列构成的矩阵A是以采空区所有待求结点压力为未知数的代数方程组(即控制方程组)的系数矩阵，因此，有
(6)
图4 总体矩阵M的分块表示
Fig. 4 The global matrix represented with block matrixes
式(6)右端列向量b可由分块矩阵B与Pb求得，即b=BPb。因此，在合成M时只需计算A和B分块。
事实上，采空区内，特别是邻近工作面的范围，一般为非线性的渗流，可用式(7)所示的Bachmat方程描述：
(7)
式中：β为介质颗粒形状系数；d为平均调和粒径，m；φ为孔隙度；υ为运动黏性系数，m2/s。本文采用文献[9]提出的对渗透系数进行迭代修正的方法，基于式(3)线型模型求解式(7)的非线性模型。
通过式(6)求得节点压力后，可通过达西定律公式V=-K▽P求得边界单元的流速，通过式(8)可求得图2所示的边界流量：
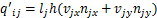(8)
式中：lj为采空区边界单元j在边界上的边长，m；h为采空区厚度，m；vjx和vjy分别为单元j在x和y方向上流速的分量，m/s；njx和njy分别为单元j所在边界的外法线方向的单位矢量在x和y方向的分量。
综上，求解耦合模型的计算量主要来自解(6)式大型稀疏线性方程组，它存在于非线性渗流迭代与图3迭代的双重循环之内，再加上多采空区同时耦合于矿井风网，其计算量是普通采空区流场模拟计算量的若干倍。
3 基于PARDISO的耦合模型求解
3.1 PARDISO特点
PARDISO是针对大型稀疏线性方程组的求解器[20]。在算法上，采用LU分解法；在性能上，采用共享内存和分布式内存的并行计算；在模块化方面，PARDISO以动态链接库向外提供封装好的函数，可以被VC++等多种语言访问。此外，PARDISO采用压缩稀疏行格式(compressed sparse row，CSR)和压缩稀疏列格式(compressed sparse column，CSC)存储系数矩阵[21]，降低对矩阵元素的访问时间。这2种格式是利用PARDISO进行耦合模型求解的关键数据结构。
3.2 基于PARDISO的耦合模型算例分析
按图2所示原理，构造图5所示算例，风网含有4条分支，分支(3)代表采煤工作面分支；采空区划分为8个单元，单元直角边长均为150 m，分支(1)设为固定风量分支，初始风量取30 m3/s。为便于对算例结果重现，对相关物理参数进行简单设定，分支的风阻均为0.05 kg/m7，单元的渗透系数K△均取0.1 m/s，采空区厚度h为6 m，平均粒径d为0.04 m，介质颗粒形状系数β取0.07，空气的运动黏性系数υ为14.6×10-6 m2/s。
图5 按图2所示原理构造的简单算例
Fig. 5 A simple example constructed according to the principle shown in Fig. 2
取节点①为基点，压力为0 Pa，按照耦合模型原理，第1次解算风网得到节点②，③和④的压力分别为135，90和45 Pa，则采空区边界节点⑤，⑧和的压力分别为90，67.5和45 Pa。首次解算采空区时，第1次迭代中得到的式(6)系数矩阵A如图6所示，图6中空格表示绝对的0值，即没有任何单元矩阵的元素合成到这些位置；非空格中的0值是由计算产生的，在条件变化时，其值可能不等于0。
图6 算例迭代中首次计算的系数矩阵
Fig. 6 Coefficient matrix for the first time in iterative calculation
采用PARDISO解算式(6)，需将图6所示矩阵的非0元素存入表1所示的3个一维数组a，Ai和Aj中。其中a存放元素值，Ai和Aj存放元素的位置信息，转存规则是：在图6中按从上到下逐行、从左到右逐列的顺序依次扫描图中的非0元素，存入a中。Ai[k]表示图6中第k行第1个非0元素在a中的序号，Aj[k]存放a[k]元素在图中的列号。用表1所示的数据结构来保存图6中的非0元素，减少了大量的存储空间。从图6可知：式(6)实际是带状方程组，带宽取决于各个单元结点序号差的最大值。为减少矩阵带宽，在有限元网格划分理论中常施加一定方法来降低带宽，提高性能。采用PARDISO引入的以上压缩存储格式后，不用再考虑带宽对性能的影响，这在一定程度上降低了对采空区网格划分的要求。
表1 图6矩阵压缩成的3个1维数组
Table 1 Three one-dimensional arrays conforming to PARDISO rules
将式(6)的右端向量b和以上3个一维数组传入PARDISO的接口，即可实现基于PARDISO的线性方程组快速求解。图5算例在风网解算与采空区流场模拟之间迭代8次后收敛，图7所示为风网分支流量、采空区单元流速及两者之间的风流交换量，节点(2)至(13)的压力依次为137.86，92.86，47.78，92.86，75.65，73.34，70.32，70.82，71.02，47.78，67.48和69.49 Pa。
图7 图5算例的模拟结果
Fig. 7 The simulation results of the example shown in Fig. 5
4 算法实现与复杂算例分析
4.1 软件开发和算例参数
本文基于VC++编制以上模型的软件，简称i-MVS (integrated mine ventilation simulator)。i-MVS采用ObjectARX技术[17]进行风网与采空区的可视化，通过动态链接库使用PARDISO，按孔隙率呈“O”形圈分布设置采空区渗透系数[22-24]，可对任意风网与平面采空区流场进行统一计算。
图8所示为由某矿2个采空区及高度简化后的风网形成的算例。工作面的微小分支按每100 m风阻为0.020 8 kg/m7设定；1号和2号这2个采煤工作面设计风量分别为30 m3/s和20 m3/s；1号工作面斜长300 m，已回采500 m；2号工作面斜长200 m，已回采300 m；采空区厚度均取6 m。2个工作面共分成161条分支，连接节点①和②的分支(风机所在位置)设为初始风量为100 m3/s的固定风量分支，连接节点⑩与的分支代表风网的其他部分，设计过风量为45 m3/s。风网共设有3个调风装置， 1号和2号位于每个工作面进、回风巷的联络巷，3号用于控制2号工作面的回风量。模型中涉及的其他参数取值与3.2节的相同。
图8 模拟算例基本情况
Fig. 8 Simulated case condition
4.2 模拟结果
4.2.1 耦合模型计算结果与性能分析
图9所示为风网及采空区在边界处耦合后的流量及流速计算结果。2个采空区分别用50条流线与等压线形成流网。不漏风的边界为流函数值为0的流线，1号和2号采空区流线间的流量差距分别为0.046 m3/s和0.025 m3/s，2个采空区总的漏风量分别为2.3 m3/s和1.2 m3/s。1号和2号采空区等压线差距分别为1 Pa和0.3 Pa，节点①和②之间的压差表明系统总阻力838.6 Pa。由图9可见：距离工作面越远，流线数量越少，采空区流量越小；大部分流线起于进风隅角，止于回风隅角，表明采空区漏风主要从工作面的2个隅角流入与流出采空区。
采空区中风速为0.001 7~0.004 0 m/s的区域代表煤自燃氧化升温带，从图9可知，1号采空区氧化升温带起始位置位于工作面后26.5 m，中心宽度为33.4 m，沿两侧边界宽度为147.1 m；2号采空区氧化升温带位于工作面后11.5 m，中心宽度为28.5 m，沿两侧边界的宽度为90.0 m。因此，当确定用于控制采空区自然发火的最小推进度时，应采用氧化升温带在采空区边界上的宽度。
图9 风网与采空区流场在边界处耦合后的计算结果
Fig. 9 Simulation results of the boundary coupling model between ventilation network and gob flow field
PARDISO求解技术的性能分析。2个采空区共有24 660个单元，12 939个节点，其中，采空区节点有12 766个。风网与采空区之间经过6次迭代后收敛(ε=10-5)，共进行了860次对式(6)的求解；在4核CPU(频率2.2 GHz)的个人电脑上，完成耦合模型计算约2 min。
4.2.2 漏风对采空区边界条件的影响
作为对比，将图3中不进行迭代、只进行1次网络解算和采空区模拟结果称为非耦合模型，进行常规的风网与采空区流场模拟。图10显示了2个工作面在2种模型漏风边界沿线的压力与漏风量，耦合模型考虑采空区漏风对边界条件的影响，得到比非耦合模型更小的漏风压差与漏风量。从图10(a)可见：1号工作面在非耦合模型中两端的压力为56.2 Pa，耦合模型中为49.9 Pa，差值为6.3 Pa，是总压力的12.6%。由图10(b)可见：2号工作面在耦合与非耦合模型下工作面压差分别为14.5 Pa与16.2 Pa，耦合模型比非耦合模型压差小1.7 Pa，占工作面总压差的12.0%。
对漏风量的比较可以得到近似的结论：1号工作面在耦合与非耦合模型中的总漏风量分别为138.0 m3/min与152.8 m3/min，相差14.8 m3/min，是耦合模型总漏风量的10.7%；2号工作面在耦合与非模型中的总漏风量分别为72.0 m3/min与80.7 m3/min，相差8.7 m3/min，是耦合模型总漏风量的12.1%。因此，12%可以视为耦合模型对常规采空区模拟方法的改进量。U形工作面通风系统的采空区漏风常小于其他形式通风系统(如Y形通风系统)。故考虑漏风对采空区流场边界条件的影响是必要的。
图10 工作面沿线压力与采空区漏风量分布
Fig. 10 Air pressures and air leakage along the working faces
图11 1号调节装置损坏后的风网流量与采空区速度场
Fig. 11 Network air distributions and gob flow field colored after NO 1 regulator damaged
4.2.3 异常通风模拟
作为对一个异常情况的分析，图11模拟了1号调风装置意外破坏后的风网流量与采空区速度场，其标注信息与图9中的相同。图8中位于节点和之间的分支的风阻为15.323 0 kg/m7，其中包含了1号调风装置风阻(15.293 8 kg/m7)和巷道风阻(0.029 2 kg/m7)。将此分支风阻从15.323 0 kg/m7降到0.029 2 kg/m7得到此异常情况下的风网与采空区流场，即图11所示结果。从图11可知：1号调风装置的损毁对2号工作面通风系统的影响相对较小，但1号工作面通风系统几乎被短路，47.00 m3/s的风流从节点直接流向节点，工作面风量从30.20 m3/s减到12.40 m3/s，同时，1号采空区漏风量从2.30 m3/s降到0.79 m3/s。工作面风量及采空区漏风量的改变将影响这些区域瓦斯浓度，假设采空区瓦斯涌出量不变，采空区漏风量的减小将导致从1号采空区涌出气体的平均瓦斯浓度增加为原来的2.9倍，加上工作面风量减小，1号工作面的危险程度将明显增加。
5 结论
1) 采煤工作面两端的压差是采空区漏风的动力，沿线的压力分布是采空区流场的定解条件、需要依靠对风网的求解来确定；而采空区漏风又会减小工作面的压差、改变沿线的压力分布。耦合模型将工作面细分成与采空区单元匹配的分支，通过将采空区边界沿线的漏风分段加入风网边界节点的流量平衡方程，导致风网解算与采空区流场模拟形成耦合关系，通过对两者的迭代计算求得更加准确的解。
2) 耦合模型实现了风网与多采空区的统一求解。矿井通风网络包括全矿井的井巷系统，耦合模型实现了采空区流场与风网在边界上的无缝连接，使过去分离解算的采空区流场可以与风网构成一个整体，不用单独为某个采空区流场设置边界条件。
3) 使用PARDISO实现了对耦合模型的高效求解。采用自编程方法实现模型，将采空区流场模拟与矿井通风网络解算功能进行了集成。采用PARDISO求解耦合模型中的大型稀疏线性方程组保证了软件的性能；使用PARDISO引入的压缩行、列存储格式使得在采空区的网格划分中不用考虑单元的结点编号对求解性能的影响。
参考文献：
[1] 李宗翔. 高瓦斯易自燃采空区瓦斯与自燃耦合研究[D]. 阜新: 辽宁工程技术大学资源与环境工程学院, 2007: 1-2.
LI Zongxiang. Study of coupling of gas and spontaneous combustion in highly gassy and spontaneous combustion goafs[D]. Fuxin: Liaoning Technical University. College of Resources and Environmental Engineering, 2007: 1-2.
[2] XIA Tongqiang, ZHOU Fubao, WANG Xinxin, et al. Controlling factors of symbiotic disaster between coal gas and spontaneous combustion in longwall mining gobs[J]. Fuel, 2016, 182: 886-896.
[3] YUAN Liming, SMITH A C. Numerical study on effects of coal properties on spontaneous heating in longwall gob areas[J]. Fuel, 2008, 87: 3409-3419.
[4] 刘剑, 贾进章, 郑丹. 流体网络理论[M]. 北京: 煤炭工业出版社, 2002: 111-129.
LIU Jian, JIA Jinzhang, ZHENG Dan. Fluid network theory [M]. Beijing: China Coal Industry Publishing House, 2002: 111-129.
[5] 厍向阳, 常新坦, 孙艺珍. 基于遗传算法的通风网络两步法风流调节优化算法[J]. 中南大学学报(自然科学版), 2011, 42(9): 2729-2736.
SHE Xiangyang, CHANG Xintan, SUN Yizhen. Optimization algorithm adjusting ventilation flow about Min ventilation networks based on two step way and genetic algorithm [J]. Journal of Central South University (Science and Technology), 2011, 42(9): 2729-2736.
[6] 王德明, 王俊, 周福宝. 基于面向对象技术开发的矿井通风图形系统[J]. 煤炭学报, 2000, 25(5): 510-513.
WANG Deming, WANG Jun, ZHOU Fubao. Developed mine ventilation graphics system based on the object-oriented technologies[J]. Journal of China Coal Society, 2000, 25(5): 510-513.
[7] 吴奉亮, 高佳南, 常心坦, 等. 矿井风网雅可比矩阵对称特性及并行求解模型[J]. 煤炭学报, 2016, 41(6): 1454-1459．
WU Fengliang, GAO Jianan, CHANG Xintan, et al．Symmetry property of Jacobian matrix of mine ventilation network and its parallel calculation model[J]. Journal of China Coal Society, 2016, 41(6): 1454-1459．
[8] 唐明云, 戴广龙, 秦汝祥, 等. 综采工作面采空区漏风规律数值模拟[J]. 中南大学学报(自然科学版), 2012, 43(4): 1494-1498.
TANG Mingyun, DAI Guanglong, QIN Ruxiang, et al. Numerical analysis of air-leakage law in goaf of fully mechanized face[J]. Journal of Central South University(Science and Technology), 2012, 43(4): 1494-1498.
[9] 李宗翔, 刘玉洲, 吴强. 采空区流场非线性渗流的改进迭代算法[J]. 重庆大学学报(自然科学版), 2008, 31(2): 186-190.
LI Zongxiang, LIU Yuzhou, WU Qiang. Improved iterative algorithm for nonlinear seepage in flow field of caving goaf[J]. Journal of Chongqing University(Natural Science Edition), 2008, 31(2): 186-190.
[10] 谭波, 牛会永, 和超楠, 等. 回采情况下采空区煤自燃温度场理论与数值分析[J]. 中南大学学报(自然科学版), 2013, 44(1): 381-387.
TAN Bo, NIU Huiyong, HE Chaonan, et al. Goaf coal spontaneous combustion temperature field theory and numerical analysis under mining conditions[J]. Journal of Central South University(Science and Technology), 2013, 44(1): 381-387.
[11] 文虎, 张泽, 赵庆伟, 等. 煤层分层前后采空区自燃“三带”的数值模拟[J]. 煤矿安全, 2017, 48(3): 178-181.
WEN Hu, ZHANG Ze, ZHAO Qingwei, et al. Numerical simulation on spontaneous combustion “three zones” of goaf before and after coal seam layering[J]. Safety in Coal Mines, 2017, 48(3): 178-181.
[12] 秦跃平, 刘伟, 杨小彬, 等. 基于非达西渗流的采空区自然发火数值模拟[J]. 煤炭学报, 2012, 37(7): 1177-1183.
QIN Yueping, LIU Wei, YANG Xiaobin, et al. Numerical simulation of impact of non-Darcy seepage on spontaneous combustion in goaf[J]. Journal of China Coal Society, 2012, 37(7): 1177-1183.
[13] 李宗翔, 衣刚, 武建国, 等. 基于“O”型冒落及耗氧非均匀采空区自燃分布特征[J]. 煤炭学报, 2012, 37(3): 484-489.
LI Zongxiang, YI Gang, WU Jianguo, et al. Study on spontaneous combustion distribution of goaf based on the “O” type risked falling and non-uniform oxygen[J]. Journal of China Coal Society, 2012, 37(3): 484-489.
[14] BRUNNER DJ. Ventilation models for longwall gob leakage simulation[C]// Proceedings of the 2nd US mine ventilation symposium. Boca Raton, FL, USA: CRC, 1985: 655-662.
[15] 魏引尚, 邵炜航, 王慧. 基于网络解算的采空区漏风分布计算模式[J].煤矿安全, 2011, 42(1):46-49.
WEI Yinshang, SHAO Weihang,WANG Hui. Calculation model of gob air leakage based on the ventilation network calculation[J]. Safety in Coal Mines, 2011, 42(1): 46-49.
[16] WEDDING W C. Multi-scale modeling of the mine ventilation system and flow through the gob[D]. Lexington, Kentucky, USA: University of Kentucky. College of Engineering, 2014: 43-66.
[17] WU Fengliang, CHANG Xintan, DAN Zhuo. A mine ventilation program integrated with gob flow field simulation[C]// Proceedings of the 11th International Mine Ventilation Congress. Singapore: Springer Singapore, 2018: 888-898.
[18] 黄光球, 陆秋琴, 姚玉霞. 大规模复杂通风网络节点风压解算方法[J]. 计算机工程, 2008, 34(4): 257-271．
HUANG Guangqiu, LU Qiuqin, YAO Yuxia. Junction’s air pressure solution for large-scale complicated ventilation networks[J]. Computer Engineering, 2008, 34(4): 257-271.
[19] 赵阳升. 有限元法及其在采矿工程中的应用[M]. 北京: 煤炭工业出版社, 1994: 49-57.
ZHAO Yangsheng. Finite element method and its application in mining engineering[M]. Beijing: China Coal Industry Publishing House, 1994: 49-57.
[20] SCHENK O, GARTNER K. Solving unsymmetric sparse systems of linear equations with PARDISO[J]. Future Generation Computer Systems, 2004, 20(3): 475-487.
[21] 曹大志, 强洪夫, 任革学. 基于OpenMP和Pardiso的柔性多体系统动力学并行计算[J]. 清华大学学报(自然科学版), 2012, 52(11): 1643-1649.
CAO Dazhi, QIANG Hongfu, REN Gexue. Parallel computing studies of flexible multibody system dynamics using OpenMP and Pardiso[J]. Journal of Tsinghua University (SCI & Tech), 2012, 52(11): 1643-1649.
[22] SHAO Hao, JIANG Shuguang, WANG Lanyun, et al. Bulking factor of the strata overlying the gob and a three-dimensional numerical simulation of the air leakage flow field[J]. Mining Science and Technology(China), 2011, 21(2): 261-266.
[23] 王少锋, 王德明, 曹凯, 等. 采空区及上覆岩层空隙率三维分布规律[J]. 中南大学学报(自然科学版), 2014, 45(3): 833-839.
WANG Shaofeng, WANG Deming, CAO Kai, et al. Distribution law of 3D fracture field of goaf and overlying strata[J]. Journal of Central South University(Science and Technology), 2014, 45(3): 833-839.
[24] 陈鹏, 张浪, 邹东起. 基于“O”形圈理论的采空区三维渗透率分布研究[J]. 矿业安全与环保, 2015, 42(5): 38-41.
CHEN Peng, ZHANG Lang, ZOU Dongqi. Study of three-dimensional distribution of permeability in gob based on O-shape circle theory[J]. Mining Safety & Environmental Protection, 2015, 42(5): 38-41.
（编辑 秦明阳）
收稿日期： 2019 -11 -04; 修回日期： 2020 -01 -23
基金项目(Foundation item)：国家自然科学基金资助项目(51974232; 51574193)；陕西省基础研究计划项目(2017JM5039) (Projects(51974232; 51574193) supported by the National Natural Science Foundation of China; Project(2017JM5039) supported by the Fundamental Research Funds of Shaanxi Province)
通信作者：吴奉亮，博士，副教授，从事矿井通风与安全研究；E-mail: wufl@xust.edu.cn
