文章编号:1004-0609(2014)11-2762-07
钨纤维增强锆基块体非晶复合材料的黏弹性响应
廖光开,龙志林,杨 妙,陈舒敏,邹 萍
(湘潭大学 土木工程与力学学院,湘潭 411105)
摘 要:基于均匀化理论建立了计算具有微观周期性结构的钨纤维增强锆基块体非晶复合材料的黏弹性力学模型;结合有限单元法在拉氏域中计算了该复合材料的等效松弛模量,用最小二乘法拟合得到用Prony级数表示的松弛模量;并进一步得到拉氏域中的蠕变柔量;然后进行拉氏逆变换,得到时间域内的等效复合模量和蠕变柔量;分析了钨纤维体积分数对复合材料等效黏弹性能的影响。结果表明,将均匀化理论与有限元方法相结合能有效地预测具有微观周期性结构的钨纤维增强锆基块体非晶复合材料的黏弹性能,进而有效地优化该类复合材料性能。
关键词:块体非晶合金复合材料;均匀化理论;有限元分析;黏弹性能
中图分类号:TG139 文献标志码:A
Viscoelastic response of tungsten fiber reinforced Zr-based bulk metallic glass matrix composites
LIAO Guang-kai, LONG Zhi-lin, YANG Miao, CHEN Shu-min, ZOU Ping
(College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China)
Abstract: Based on the homogenization theory, a mechanical model to calculate the viscoelastic properties of tungsten fiber reinforced Zr-based bulk metallic glass matrix composites (W/Zr-BMGMCs) with periodic microstructure was formulated. The equivalent relaxation modulus of this composite material was then calculated in the Laplace domain combined with the finite element method. The creep compliance in the Laplace domain can be further achieved through the relaxation modulus expressed by Prony series fitted with the method of least squares. Consequently, equivalent composite modulus and creep compliance in the time domain can be obtained by means of inverse Laplace transform Laplace inverse transform Laplace inverse transform Laplace inverse transf. The effects of the volume fraction of tungsten fiber on the equivalent viscoelastic properties of (W/Zr-BMGMCs) were further studied. The results demonstrate that a combined approach of the homogenization theory and the finite element formulation can effectively anticipate the viscoelastic properties of (W/Zr-BMGMCs) with periodic microstructure, and thus provide basis for effective optimization of this kind of composites.
Key words: bulk metallic-glass matrix composite; homogenization theory; finite element analysis; viscoelastic property
钨纤维增强锆基块体非晶合金作为一种新型高级的复合材料,克服了块体非晶合金低塑形变形能力的缺陷[1-3]。钨纤维的引入极大地提高了这类复合材料的韧性[4-6],使得钨纤维增强锆基块体非晶合金在军工、航天和体育等领域具有广阔的应用前景[7]。钨纤维增强锆基块体非晶合金在长期负载或高温环境下会呈现出明显的黏弹性特性 (如松弛和蠕变现象),从而严重影响该类材料的工程应用。因此,预测和实验研究钨纤维增强锆基块体非晶合金的黏弹性能对于推动该类复合材料力学性能的基础研究和实际应用具有重要意义。
近年来,随着钨纤维增强锆基块体非晶合金在工程界的广泛应用,国内外学者对其力学性能进行了大量实验研究[1],涉及其刚度、强度、断裂和损伤等多方面。但现阶段对其黏弹性能的研究还鲜见报道,尚处于探索阶段,迫切需要理论研究的深入。目前,对复合材料黏弹性能的研究方法大体上可分为3大类:1) 建立理论模型进行理论研究;2) 蠕变实验研究;3) 结合理论模型采用有限元方法研究。在理论研究方面,主要采用的模型有Burgers体模型[8]、自洽模型[9]、Eshelby模型[10]和新构造模型。这几种模型在分析之前都进行了较多的假设,其分析结果和材料的实际情况存在偏差,具有一定的局限性,不能精确地描述材料的应力应变场。随着国内外学者多年来的深入研究,将均匀化理论模型[11-12]运用在黏弹性能分析上[13-14],综合考察了纤维取向、界面和增强相的几何结构等多方面因素对黏弹性能的影响。同时,随着计算机技术的不断发展,有限元方法被广泛应用于复合材料的数值分析。将均匀化理论与有限元计算有效结合,有望对钨纤维增强锆基块体非晶合金的多尺度黏弹性能进行深入细致的研究。
本文作者根据钨纤维增强锆基块体非晶合金 (W/Zr52.5Ti5Cu17.9Ni14.6Al10)的微观周期性结构特点,基于均匀化理论建立了计算该类复合材料的黏弹性力学模型。将该模型与有限元法相结合,利用Visual C++语言编写了均匀化理论的有限元计算程序,对钨纤维增强锆基块体非晶合金在拉氏域中的等效松弛模量进行了计算,并用最小二乘法拟合得到用Prony级数表示的松弛模量;进一步得到拉氏域中的蠕变柔量。进行拉氏逆变换,得到时间域内等效松弛模量和蠕变柔量。研究了钨纤维的体积分数对钨纤维增强锆基块体非晶合金复合材料等效黏弹性能的影响。
1 黏弹性能的渐近均匀化
图1所示为钨纤维增强锆基块体非晶合金复合材料的宏观结构、周期性微结构和单胞示意图。如图1(a)所示,设钨纤维增强锆基块体非晶合金复合材料在三维空间中占据区域为 ,其细观结构可看成是非均质单元在空间的周期性重复排列。设该物体受体积力f,力边界Γt上的表面力t, 以及位移边界Γv上的给定位移
,其细观结构可看成是非均质单元在空间的周期性重复排列。设该物体受体积力f,力边界Γt上的表面力t, 以及位移边界Γv上的给定位移 的作用。复合材料的等温黏弹性本构方程和基于虚功原理[15]表示的控制方程分别为
的作用。复合材料的等温黏弹性本构方程和基于虚功原理[15]表示的控制方程分别为
 (1)
(1)

 (2)
(2)
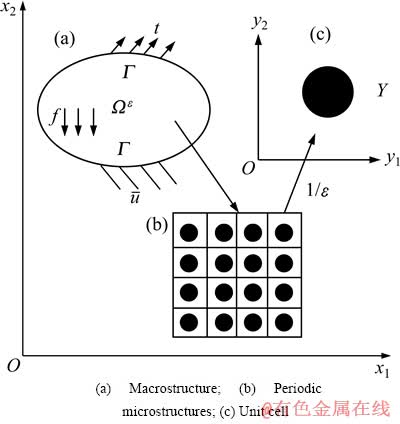
图1 钨纤维增强锆基块体非晶合金复合材料的宏观结构、周期性微结构和单胞示意图
Fig. 1 Tungsten fiber reinforced Zr-based bulk metallic glass matrix composites
式中: 和
和 分别表示应力和应变张量;
分别表示应力和应变张量;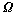 和
和 分别表示复合材料区域及其边界;
分别表示复合材料区域及其边界; 表示松弛模量;f、t和u分别表示材料所受的宏观体力、面力以及位移矩阵。根据微观力学中的对应性原理[16]可知,材料的黏弹性本构方程和弹性本构方程对时间的Laplace变换有相似对应性,即用Laplace域中的黏弹性值代替相应的弹性值,通过Laplace逆变换可得到时间域的黏弹性值。对式(2)进行Laplace变换得到在Laplace域中的黏弹性控制方程
表示松弛模量;f、t和u分别表示材料所受的宏观体力、面力以及位移矩阵。根据微观力学中的对应性原理[16]可知,材料的黏弹性本构方程和弹性本构方程对时间的Laplace变换有相似对应性,即用Laplace域中的黏弹性值代替相应的弹性值,通过Laplace逆变换可得到时间域的黏弹性值。对式(2)进行Laplace变换得到在Laplace域中的黏弹性控制方程
 (3)
(3)
根据均匀化理论思想[11],在具有细观周期性单胞的结构中,结构场变量可用x和 两种宏细观尺度来描述。将宏观尺度下位移场
两种宏细观尺度来描述。将宏观尺度下位移场 展开成关于小参数
展开成关于小参数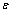 的渐近级数:
的渐近级数:
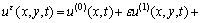
 (4)
(4)
由 及链式法则得
及链式法则得
 (5)
(5)
对式(4)和(5)进行Laplace变换并代入(3)可得宏观均匀化控制方程:
 (6)
(6)
其中 为宏观等效松弛模量的Laplace变换式,由下式确定:
为宏观等效松弛模量的Laplace变换式,由下式确定:
 (7)
(7)
式中:1/|Y|表示在单胞域上进行平均,Y为复合材料单胞尺度; 为单胞域上的位移场,可由下式确定:
为单胞域上的位移场,可由下式确定:
 (8)
(8)
借助有限元技术及数值算法求出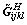 ,根据Laplace域中
,根据Laplace域中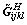 与
与 的卷积关系式可求得
的卷积关系式可求得 ,对
,对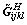 和
和 进行Laplace逆变换可进一步求得宏观域中黏弹性复合材料的等效松弛模量
进行Laplace逆变换可进一步求得宏观域中黏弹性复合材料的等效松弛模量 及蠕变柔量
及蠕变柔量 。以下将基于以上方法研究钨纤维增强锆基块体非晶合金复合材料的黏弹性能。
。以下将基于以上方法研究钨纤维增强锆基块体非晶合金复合材料的黏弹性能。
2 黏弹性能分析
钨纤维增强锆基块体非晶合金属于单向纤维复合材料,具有微观周期性[17],其增强相钨纤维是一种弹性材料,性能不随温度和时间变化,在基体中呈正方形点阵分布(见图1(b))。设钨纤维为横观各向同性材料,进行有限元计算时单胞可取为内部含有单根圆形截面纤维的正方体,其有限元网格模型如图2所示。
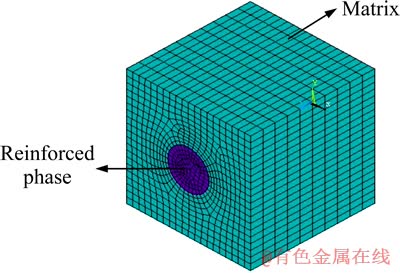
图2 钨纤维增强锆基块体非晶合金三维单胞网格模型
Fig. 2 Three-dimensional grid cell model of tungsten fiber reinforced Zr-based bulk metallic glass matrix composites
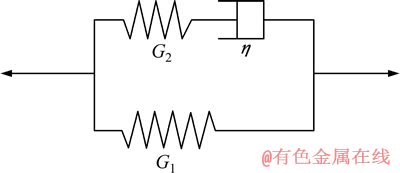
图3 Zener体模型示意图
Fig. 3 Schematic diagram of model of Zener body
锆基块体非晶基体是一种典型的黏弹性材料,其体积变形为弹性变形,而剪切变形可以用Zener体黏弹性模型(示意图如图3所示)来模拟[18],其本构关系为
 (9)
(9)
 (10)
(10)
其全量表达式为
 (11)
(11)
式中:K和D分别为体积模量和剪切模量,其中D可表示为
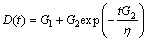 (12)
(12)
式中:G1和G2为锆基块体非晶基体的剪切刚性模量;η为黏度系数。
松弛模量G可表示为
 (13)
(13)
本研究中,设钨纤维增强锆基块体非晶合金复合材料具有线性黏弹性质,其黏弹性本构关系可用Zener体模型模拟,松弛模量表示成Prony级数[19]形式,当级数仅取一项时松弛模量及其Laplace变化可表示为式(14a),通过式(14b)对其松弛模量进行曲线拟合。
 (14a)
(14a)
 (14b)
(14b)
式中:A、B和C均为Zener体模型的元件参数。设 表示终值模量;
表示终值模量;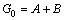 表示初始模量;
表示初始模量; 表示应力松弛时间。
表示应力松弛时间。
运用弹性分析所采用的网格化方法和边界条件(单胞网格模型如图2所示),通过有限元求解微观均匀化问题式(7),并控制时间子步,得到不同离散时间点上的拉氏参数s对应的 ,利用最小二乘法拟合得到式(12)的3个黏弹性参数为A、B和C,通过Laplace逆变化求得时间域内的
,利用最小二乘法拟合得到式(12)的3个黏弹性参数为A、B和C,通过Laplace逆变化求得时间域内的 。蠕变柔量可根据下式得到
。蠕变柔量可根据下式得到
 (15)
(15)
具体表达式为
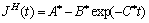 (16)
(16)
式中:A*、B*和C*均为A、B和C的数学表达式; 表示初始蠕变柔量;
表示初始蠕变柔量;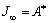 表示终值蠕变柔量;蠕变延迟时间
表示终值蠕变柔量;蠕变延迟时间 。
。
3 结果与讨论
依据前文方法,利用Visual C++语言编写均匀化理论的计算程序,计算钨纤维增强锆基块体非晶合金复合材料的等效黏弹性能。利用图2所示的有限元网格模型进行均匀化理论计算。在图2所示的有限元单胞中,基体和增强相都呈对称分布,设钨纤维为横观各向同性材料,弹性常数为Ew=410 GPa,泊松比μw=0.28。设锆基块体非晶合金基体(Zr52.5Ti5Cu17.9Ni14.6Al10)为各向同性材料,其室温下的黏弹性参数由纳米压痕加载阶段的载荷-位移关系式(17) 对不同加载速率下的实验数据[18]进行线性拟合,并取平均值得到,拟合曲线如图4所示[19]。

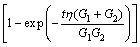 (17)
(17)
式中:h(t)和F(t)分别表示纳米压痕实验过程中的位移和载荷; 为加载速率;取球形压头半径R=5 μm;锆基块体非晶泊松比μBMG=0.363。对不同加载速率下的实验数据拟合,并取平均值得到室温下的锆基块体非晶合金黏弹性参数G1=28.1 GPa,G2=10.3 GPa,η=28.3 MPa·s,
为加载速率;取球形压头半径R=5 μm;锆基块体非晶泊松比μBMG=0.363。对不同加载速率下的实验数据拟合,并取平均值得到室温下的锆基块体非晶合金黏弹性参数G1=28.1 GPa,G2=10.3 GPa,η=28.3 MPa·s, 。
。
利用所得参数计算钨纤维体积分数φf=20%时的复合模量 并与Voigt模型[20]、Eshelby模型[10]及文献[21]中报道的模型预测结果进行比较,结果如图5所示。
并与Voigt模型[20]、Eshelby模型[10]及文献[21]中报道的模型预测结果进行比较,结果如图5所示。
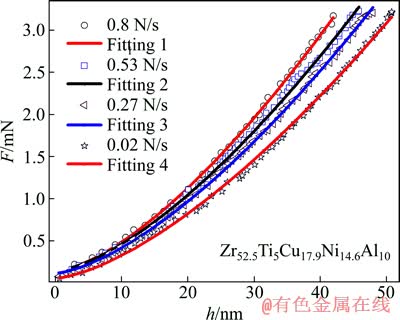
图4 锆基块体非晶合金黏弹性参数拟合曲线图[19]
Fig. 4 Curves of fitting viscoelastic parameters of Zr-based bulk metallic glass[19]
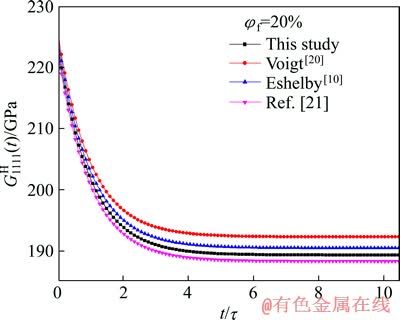
图5 不同模型预测的复合材料等效松弛模量( )随无量纲时间(t/τ)的变化关系
)随无量纲时间(t/τ)的变化关系
Fig. 5 Variation of equivalent relaxation modulus ( ) predicted by different models with dimensionless time (t/τ) for composites
) predicted by different models with dimensionless time (t/τ) for composites
由图5可以看出:本研究中建立的模型预测结果与其他模型的结果相近,不同模型预测的初始模量值 及松弛时间τ都基本相等,但终值模量
及松弛时间τ都基本相等,但终值模量 与其他模型结果却存在一定差异,这可能是本模型在有限元计算时单胞网格划分过于稀疏,以及用最小二乘法拟合过程中对数据的处理存在误差。从图5还可以看出,本研究中建立的模型预测的初始模量值
与其他模型结果却存在一定差异,这可能是本模型在有限元计算时单胞网格划分过于稀疏,以及用最小二乘法拟合过程中对数据的处理存在误差。从图5还可以看出,本研究中建立的模型预测的初始模量值 =223.3 GPa与文献[22]预测的弹性模量值
=223.3 GPa与文献[22]预测的弹性模量值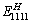 =224.7 GPa基本相等,间接地说明了该方法的有效性和合理性。
=224.7 GPa基本相等,间接地说明了该方法的有效性和合理性。
为了研究钨纤维体积分数φf对复合材料的整体黏弹性能的影响,分别计算了不同钨纤维体积分数下等效松弛模量和等效蠕变柔量(见图6和7)。由计算结果可以看出,随着钨纤维体积分数的增加,初始模量和终值模量都逐渐增大,与宏观弹性模量的变化规律基本一致。而初始柔量和终值柔量随着钨纤维体积分数的增加都稍呈下降趋势,这可能是由于钨纤维的引入抑制了非晶基体中的黏性流动。从计算结果还可看出,不同钨纤维体积分数下的应力松弛时间τ和蠕变延迟时间τ*与基体的相近,说明了该复合材料与其非晶基体具有相近的黏性系数η,其黏性性能主要来自非晶基体的贡献。
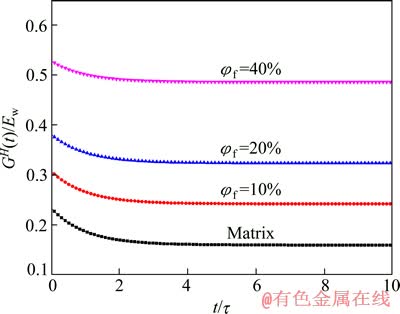
图6 不同钨纤维体积分数时复合材料的无量纲等效松弛模量(GH(t)/Ew)随无量纲时间(t/τ)的变化关系
Fig. 6 Variation of dimensionless equivalent relaxation modulus (GH(t)/Ew) with dimensionless time (t/τ) for studied composites with different volume fractions of W fiber
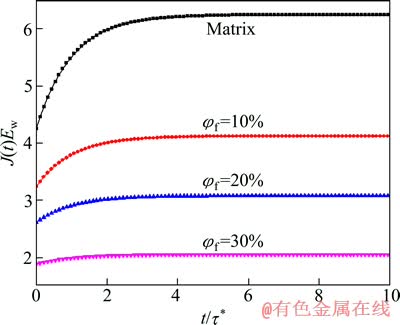
图7 不同钨纤维体积分数时复合材料的无量纲等效蠕变柔量(J(t)Ew)随无量纲时间(t/τ*)的变化关系
Fig. 7 Variation of dimensionless equivalent creep compliance (J(t)Ew) with dimensionless time(t/τ*) for composites with different volume fractions of W fiber
为直观地研究钨纤维体积分数对黏弹性效应的影响,定义初始模量和终值模量的差值与初始模量的比值为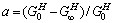 ,终值柔量和初始柔量的差值与终值柔量的比值为
,终值柔量和初始柔量的差值与终值柔量的比值为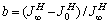 。对于不同钨纤维体积分数的复合材料,比值a和b大小直接体现了材料的黏弹性效应的强弱[23],比值a和b越大,黏弹性效应越强;比值a和b越小,黏弹性效应越弱。不同体积分数下复合材料的黏弹性效应计算结果及文献[24]中钨纤维体积分数对压缩断裂能的影响如图8所示。
。对于不同钨纤维体积分数的复合材料,比值a和b大小直接体现了材料的黏弹性效应的强弱[23],比值a和b越大,黏弹性效应越强;比值a和b越小,黏弹性效应越弱。不同体积分数下复合材料的黏弹性效应计算结果及文献[24]中钨纤维体积分数对压缩断裂能的影响如图8所示。
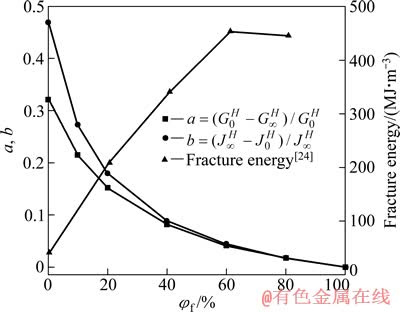
图8 不同钨纤维体积分数下复合材料的a、b值及断裂能[24]
Fig. 8 Values of a and b and fracture energy of composites with different volume fractions[24]
由图8得到,随着钨纤维体积分数的增加,复合材料的松弛效应和蠕变效应都逐渐减弱,说明钨纤维的引入有效地阻碍了单一剪切带的滑移,促进了多重剪切带的产生,使非晶基体的弹性性能得到增强,降低了其黏性性能,提高了复合材料的韧性。在钨纤维体积分数小于40%时,复合材料的蠕变效应明显大于松弛效应,且在这一比率区间内两种效应的下降速率都比较快,说明在这一区间内,钨纤维的增强作用对复合材料的等效黏弹性能影响较大,且蠕变效应大于松弛效应。钨纤维体积分数在40%~60%这一区间内两种效应逐渐趋同,但蠕变效应依然略大于松弛效应。钨纤维体积分数大于60%时两种效应基本一致,且变化曲线平稳。这一变化规律与钨纤维增强锆基块体非晶复合材料(W/Zr38Ti17Cu10.5Co12Be22.5)压缩断裂能曲线[24]的斜率变化规律(见图8)有相类似之处;同时,文献[24]的研究结果表明,在压缩断裂过程中,当钨纤维增强锆基块体非晶复合材料(W/Zr38Ti17Cu10.5Co12Be22.5)钨纤维体积分数小于 40%时为剪切破坏;在 40%~60%之间时为钨纤维的弯曲、扭转后劈裂;而钨纤维体积分数大于 60%时,复合材料沿纵向劈裂。但该类复合材料的黏弹性效应与断裂机理的相关性还有待进一步的探讨。
4 结论
1) 基于均匀理论建立了计算具有微观周期性结构的钨纤维增强锆基块体非晶合金复合材料黏弹性能的力学模型。结合有限元方法对该复合材料的等效黏弹性能进行预测,预测结果与其他模型结果相近。均匀化方法是一种具有严格数学依据、高效而实用的方法,在预测钨丝增强锆基块体非晶复合材料等效黏弹性方面具有相对较强的优势。
2) 通过计算考察了钨纤维体积分数对复合材料的等效松弛模量及等效蠕变柔量的影响,并进一步分析了钨纤维体积分数对整体黏弹性效应的影响。随着体积分数的增加,初始模量和终值模量都逐渐增大,而初始柔量和终值柔量随着钨纤维体积分数的增加都稍呈下降趋势,说明钨纤维的引入能有效抑制非晶基体的黏性流动,提高了复合材料的韧性;复合材料的黏性主要来自非晶基体的贡献;同时得到的等效黏弹性效应曲线图与前人的实验结果存在着一定的对应性。研究结果为进一步确定钨丝增强锆基块体非晶合金的成分设计和微观应力,奠定了有力的理论基础。
REFERENCES
[1] 张晓立, 王金相, 孙宇新, 付艳恕, 刘家骢. 钨丝增强块体非晶复合材料的研究进展[J]. 稀有金属材料与工程, 2008, 37(8): 1323-1328.
ZHANG Xiao-li, WANG Jin-xiang, SUN Yu-xin, FU Yan-shu, LIU Jia-cong. Study progress of tungsten-fiber reinforced bulk metallic-glass matrix composites[J]. Rare Metal Materials and Engineering, 2008, 37(8): 1323-1328.
[2] 姜 斐, 陈 光, 王志华, 高 度. 钨丝/非晶复合材料的制备方法和力学行为研究进展[J]. 稀有金属材料与工程, 2011, 40(7): 426-430.
JIANG Fei, CHEN Guang, WANG Zhi-hua, GAO Du. Research progress of preparation method and mechanical behavior of tungsten fiber reinforced metallic glass matrix composites[J]. Rare Metal Materials and Engineering, 2011, 40(7): 426-430.
[3] PEKER A, JOHNSON W L. A highly processable metallic glass Zr41.2Ti13.8Cu12.5Ni10.0Be22.5[J]. Applied Physics Letters, 1993, 63(17): 2342-2344.
[4] 许 福, 龙志林, 彭 建, 张 平. 块体非晶合金剪切带的原子力纳米压痕行为[J]. 中国有色金属学报, 2011, 21(6): 1444-1449.
XU Fu, LONG Zhi-lin, PENG Jian, ZHANG Ping. Atomic force microscope nanoindentation behavior of shear bands of bulk metallic glasses[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(6): 1444-1449.
[5] 杨元政, 董振江, 仇在宏, 陈小祝, 谢致薇, 白晓军. 块体非晶合金Cu58Zr20Ti20Mo2的形成与力学性能[J].中国有色金属学报, 2007, 17(7): 1090-1095.
YANG Yuan-zheng, DONG Zhen-Jiang, QIU Zai-hong, CHEN Xiao-zhu, XIE Zhi-wei, BAI Xiao-jun. Formation and mechanical properties of Cu58Zr20Ti20Mo2 bulk metallic glass[J]. Chinese Journal of Nonferrous Metals, 2007, 17(7): 1090-1095.
[6] BRUCK H A, CHRISTMAN T, ROSAKIS A J, JOHNSON W L. Quasistatic constitutive behavior of Zr41.25Ti13.75Ni10Cu12.5Be22.5 bulk amorphous alloys[J]. ScriptaMaterialia, 1994, 30(4): 429-434.
[7] 马卫锋, 寇宏超, 李金山, 陈春生, 杜三明, 周 廉, 付恒志. 钨丝增强Zr基非晶复合材料动态力行为及断裂特性[J]. 中国有色金属学报, 2008, 18(6): 1045-1050.
MA Wei-feng, KOU Hong-chao, LI Jin-shan, CHEN Chun-sheng, DU San-ming, ZHOU Lian, FU Heng-zhi. Dynamic mechanical behaviors and fracture characteristic of tungsten fiber reinforced Zr-based metallic glass matrix composites[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(6): 1045-1050.
[8] 刘文辉, 张新明, 张淳源. 均匀化方法在粘弹性多层复合材料中的应用[J]. 计算力学学报, 2005, 22(6): 722-727.
LIU Wen-hui, ZHANG Xin-ming, ZHANG Chun-yuan. Application of homogenization theory to viscoelastic multilayered composites[J]. Chinese Journal of Computational Mechanics, 2005, 22(6): 722-727.
[9] HILL R. A self-consistent mechanics of composite materials[J]. Journal of the Mechanics and Physics of Solids, 1965, 13(4): 213-222.
[10] BARBERO E J, LUCIANO R. Micromechanical formulas for the relaxation tensor of linear viscoelastic composites with transversely isotropic fibers[J]. International Journal of Solids and Structures, 1995, 32(13): 1859-1872.
[11] HASSANI B, HINTON E. A review of homogenization and topology optimization I—Homogenization theory for media with periodic structure[J]. Computer & Structures, 1998, 69: 707-717.
[12] HASSANI B, HINTON E. A review of homogenization and topology opimization II—Analytical and numerical solution of homogenization equations[J]. Computers & Structures, 1998, 69: 719-738.
[13] 刘书田, 马 宁. 粘弹性复合材料热应力松弛与本构关系研究(Ⅰ): 理论分析[J]. 复合材料学报, 2005, 22(1): 152-157.
LIU Shu-tian, MA Ning. Study on the thermal stress relaxation and constitutive equations of viscoelastic composite materials, part Ⅰ: General theory [J]. Acta Materiae Compositae Sinica, 2005, 22(1):152-157.
[14] 刘书田, 马 宁. 粘弹性复合材料热应力松弛与本构关系研究(П): 数值分析[J]. 复合材料学报, 2005, 22(1): 158-163.
LIU Shu-tian, MA Ning. Study on the thermal stress relaxation and constitutive equations of viscoelastic composite materials, part П: Numerical simulation[J]. Acta Materiae Compositae Sinica, 2005, 22(1): 158-163.
[15] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003: 46-47.
WANG Xu-cheng. Finite element method[M]. Beijing: Tsinghua University Press, 2003: 46-47.
[16] 魏培君, 张双寅, 吴永礼. 黏弹性力学的对应原理及其数值反演方法[J]. 力学进展, 1999, 29(3): 317-330.
WEI Pei-jun, ZHANG Shuang-yin, WU Yong-li. Correspondence principles and numerical methods of inverse integral transformation in viscoelastic mechanics[J]. Advances of Mechanics, 1993, 29(3): 317-330.
[17] DRAGOI D, 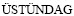 E, CLAUSEN B, BOURKE M A M. Investigation of thermal residual stresses in tungsten-fiber/bulk metallic glass matrix composites[J]. Scripta Materialia, 2001, 45: 245-252.
E, CLAUSEN B, BOURKE M A M. Investigation of thermal residual stresses in tungsten-fiber/bulk metallic glass matrix composites[J]. Scripta Materialia, 2001, 45: 245-252.
[18] HUO L S, ZENG J F, WANG W H, LIU C T, YANG Y. The dependence of shear modulus on dynamic relaxation and evolution of local structural heterogeneity in a metallic glass[J]. Acta Materialia, 2013, 61: 4329-4338.
[19] ZAK A R. Structural analysis of realistic solid-propellant materials[J]. Journal of Spacecraft and Rockets, 1968, 5(3): 270-275.
[20] SHEN T K, HING P. Ultrasonic through transmission method of evaluation the modulus of elasticity of Al2O3-ZrO2 composite[J]. Journal of Materials Science, 1997, 32: 6633-6638.
[21] ZHANG W M, ZHANG P, DENG X H, ZHANG C Y. Prediction of the viscoelastic properties of the equivalent particle for the intercalated multi-layer stack of nanoplastics[J]. Acta Mechanica Solida Sinica, 2007, 20(4): 317-323.
[22] 廖光开, 李乡安, 邹 萍, 陈舒敏, 龙志林. 基于均匀化方法的钨丝增强锆基块体非晶复合材料等效弹性常数预测[J]. 中国有色金属学报, 2014, 24(6): 1449-1458.
LIAO Guang-kai, LI Xiang-an, ZOU Ping, CHEN Shu-min, LONG Zhi-lin. Homogenization-based approach for predicting equivalent elastic constants of tungsten fiber reinforced Zr-based bulk metallic glass matrix composites[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(6): 1449-1458.
[23] 袁 欣, 孙慧玉. 三维四向编织复合材料的黏弹性能[J]. 复合材料学报, 2012, 29(2): 167-171.
YUAN Xin, SUN Hui-yu. Viscoelastic properties of 3D 4-directional braided composites[J]. Acta Materiae Compositae Sinica, 2012, 29(2): 167-171.
[24] 武晓峰, 张海峰, 胡壮麒. W丝/Zr-Ti-Cu-Ni-Be-Co非晶基复合材料的制备与塑性变形[J]. 辽宁工学院学报, 2005, 25(2): 102-107.
WU Xiao-feng, ZHANG Hai-feng, HU Zhuang-qi. Synthesis and plastic deformation of tungsten fiber reinforced bulk metallic glass matrix composite W-fiber/Zr-Ti-Cu-Ni-Be-Co[J]. Journal of Liaoning Institute of Technology, 2005, 25(2): 102-107.
(编辑 龙怀中)
基金项目:国家自然科学基金资助项目(51471139,51071134);湖南省自然科学基金重点项目(12JJ2024);湖南省研究生科研创新项目(CX2014B278)
收稿日期:2014-02-16;修订日期:2014-07-20
通信作者:龙志林,教授,博士;电话:0731-58298287;E-mail:longzl@xtu.edu.cn