Trans. Nonferrous Met. Soc. China 26(2016) 1938-1945

Feasibility of stochastic gradient boosting approach for predicting rockburst damage in burst-prone mines

Jian ZHOU, Xiu-zhi SHI, Ren-dong HUANG, Xian-yang QIU, Chong CHEN

School of Resources and Safety Engineering, Central South University, Changsha 410083, China

Received 14 January 2016; accepted 6 June 2016

Abstract: The database of 254 rockburst events was examined for rockburst damage classification using stochastic gradient boosting (SGB) methods. Five potentially relevant indicators including the stress condition factor, the ground support system capacity, the excavation span, the geological structure and the peak particle velocity of rockburst sites were analyzed. The performance of the model was evaluated using a 10 folds cross-validation (CV) procedure with 80% of original data during modeling, and an external testing set (20%) was employed to validate the prediction performance of the SGB model. Two accuracy measures for multi-class problems were employed: classification accuracy rate and Cohen’s Kappa. The accuracy analysis together with Kappa for the rockburst damage dataset reveals that the SGB model for the prediction of rockburst damage is acceptable.

Key words: burst-prone mine; rockburst damage; stochastic gradient boosting method

1 Introduction

Rockburst damage prediction is one of the most serious worldwide problems in burst-prone mines (Fig. 1) [1-4]. The occurrence of rockbursting usually involves violent failures and ejection of large quantities of rock, ranging from a fraction of a cubic meter to thousands of cubic meters, especially, rock particles can be ejected with a velocity of 8-50 m/s [5,6]. Because of the sudden time and uncertain places for rockburst, catastrophic rockbursts can lead to fatalities, injuries, damage to mine infrastructure and/or equipment, premature mine closures with abandonment of large reserves, and loss of production [4,5]. Over the years, it still occurs and remains a serious problem in the mining industry. Nowadays, rock excavations can reach great depths, and with the increased development of mining activities worldwide, the problem of rockbursting is likely to become worse [7]. Therefore, the prediction of the rockburst damage is very important and necessary for disaster prevention and migration.

Despite it is very hard to accurately predict the rockburst during excavation, extensive rockburst researches have been conducted in South Africa, Australia, Canada, China, and other countries [1,5,7]. As noted by ZHOU et al [5], different methods of estimating and predicting rockburst such as empirical criteria, in situ testing methods, and preliminary and qualitative judgment prediction methods have been proposed and often applied in practice [7-12]. Meanwhile, much work related to the prediction of rockburst has been conducted by numerical simulations [13,14]. These methods or criteria have been used with local monitoring data and laboratory tests to study the mechanical characters of rockbursts. Notwithstanding these earlier works, numerous approaches for rockburst prediction have been developed based on neural networks [15], Fisher discriminant analysis [16], hybrid [12] or ensemble techniques [17] and supervised learning techniques [5]. These collective efforts have greatly improved the prediction of rockbursting. However, few approaches have been found to be particularly successful. Obviously, only one empirical criterion could not satisfy the prediction accuracy especially for a specific underground engineering. Each of the numerical methods has its advantages and weaknesses, but the estimation of reliable values of model input parameters is found to be an increasingly difficult task [5]. Moreover, it is not convinced that the indicators from the laboratory test of rock sample are sufficient to judge the occurrence of rockbursts damage. Meanwhile, as stated by ZHOU et al [5,12], the rockburst is strongly site-specific, depending upon many factors including in-situ stress, rock mass strength, tunnel geometry, excavation methods, discontinuities and/or the activation of faults due to mining operation. Therefore, it is still considerable challenge for understanding and predicting rockbursts damage in burst prone ground.

Fig. 1 Rockburst phenomena in burst-prone grounds [4]

Stochastic gradient boosting (SGB) (also called gradient boosting machine), as a relatively new tree-based pattern recognition method, has been proposed by FRIEDMAN [18] to optimize predictive performance [19]. Owing to the merits of a limited number of user-defined parameters and the ability to model non-linear relationships, managing qualitative and quantitative variables, remaining robust despite missing data and outliers, the SGB model has been widely applied and shown considerable success in various scientific fields, e.g., pillar stability [20], skin flavonoid content [21], residential structures damage [22], land cover mapping [23] and organic carbon concentration mapping [24]. However, the performance of SGB model has not yet been attempted in recent rockburst damage studies. Therefore, it is motivated to investigate the capability of SGB in rockburst damage prediction. The main objective of this study is to investigate the feasibility of using the SGB classification model to predict rockburst damage in burst-prone mines, so that early warning can be provided to mine management for appropriate actions to reduce damage and save lives.

2 Predictive modeling

2.1 SGB classifier

SGB is a hybrid machine learning algorithm that combines both the advantages of bagging and boosting procedures. The SGB can be applied for the purposes of classification and regression [18, 19]. The term rockburst damage refers to the classification task. For multiple classification (K>2), the surrogate loss function can be considered as the following equation [18,22]:

      (1)

where y_k=1 (class=k) ∈{0, 1}, k is the number of class values (k=1,2,…, K).

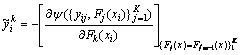
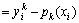                          (2)

Thus, K-trees are induced, each to predict the corresponding current residuals . This

produces K-trees each with L-terminal nodes at iteration m, {R_klm}. As mentioned above, a separate line search is performed in each terminal node l of each tree k,

           (3)

where  _k=-y_klog[p_k(x)].

There are three main hyper-parameters for tuning the SGB model [22, 25, 26]: M is the total number of boosting iterations (n.trees), v is the learning rate (shrinkage coefficient) and J is the number of terminal nodes (tree size). All computation and data analyses are implemented using the open source software R (Vision 3.02) [27].

2.2 Evaluation of SGB performance

Till now, there is no generally accepted measure of performance for multiclass models. The predictive power of SGB algorithm on rockburst damage data is evaluated by the classification accuracy rate and the Cohen’s Kappa coefficient [5,20,22,28]. The prediction accuracy is defined as the fraction of records that is correctly allocated by the model about the overall number of records among the classification models [5,20]. The Kappa index [28] measures the proportion of correctly classified units after the probability of chance agreement is removed. Let x be an K×K error matrix set out in rows and columns that express the number of sample plots (of which there are n) predicted to belong to one of K classes about the true class label. Thus, the classification accuracy (A) and the Kappa index can be obtained using the following expressions:

                         (4)

                    (5)

where x_ii is the cell count in the main diagonal, n is the number of examples, and x._i and x_i^. are the columns and rows total counts, respectively.

3 Application of SGB approach for rockburst damage prediction

3.1 Mechanisms of rockburst damage

Various rockburst mechanisms have been proposed by some researchers. ORTLEPP and STACEY [6] made a distinction between the seismic source mechanism and the rockburst damage mechanism, while KAISER et al [2] used the term modes of failure (Fig. 2) to describe the same occurrences, which has been adopted by the Australian Centre for Geomechanics (ACG) in its generic seismic risk management plan for underground hard rock mines [29]. MISICH and LANG [30] also investigated a more detailed rockburst classification system which defined rockbursts by the source mechanism and the damage mechanism that occurred at the excavation boundary.

Fig. 2 Schematic drawing showing three rockburst damage mechanisms (Modified from Ref. [2])

Fig. 3 Span definition plan view

3.2 Indictor analysis

Apparently, the rockbursting is associated with the stress in the earth’s crust, rock properties and the presence of groundwater and the structures of the rock masses [5]. Many single indicators or criteria for evaluating the occurrence and intensity of rockbursts have been presented based on the analysis of the rockburst phenomenon from different perspectives [12]. DURRHEIM et al [31] investigated 21 rockbursts which caused damage to excavations in deep South African gold mines, and found that the source mechanism of rockbursts is often controlled by the mine layout and regional structures, whileas local rock conditions and support systems strongly influenced the location and severity of rockburst damage. Obviously, the mines below the earth surface were excavated with a confining environment-defined by stresses in the earth’s crust [32,33]. Thus, the stress condition surrounding an excavation is an important factor in designing underground excavations and contributes to the level of damage induced by dynamic loading of a rock mass. HEAL et al [29] defined the stress condition factor (SCF), F_SC, as the fraction of static loading to the intact strength of the rock in Eq. (6). The excavation span (ES) often has a direct influence on the depth of failure for gravity related falls of ground and dynamic rock mass failures [32], the meaning of span refers to the width of an underground opening in plan view, as illustrated in Fig. 3. In general, the span can be determined through the largest diameter of a circle within an underground excavation [34]. Ground support system capacity (GSSC) reveals the dynamic strength of a rock mass, reducing the likelihood of rock mass failure [29]. The influence of geological structure (GS) factor accounts for favourable and unfavourable rock mass conditions which may hinder or enhance dynamically driven rock mass failure [29, 32]. Meanwhile, considerable research efforts, made by MCGARR [35], ORTLEPP and STACEY [6], KAISER et al [2] and QIU et al [36], have been devoted to estimating the peak particle velocity (PPV) and many empirical scaling laws have been derived, apparently, these equations mainly focus on the attenuate relation of PPV at the rockburst source to scale distance.

F_SC =100×σ_1T/UCS                            (6)

where σ_1T is the total maximum principal stress in the vicinity of the workplace been evaluated, MPa; UCS is the intact uniaxial compressive strength (UCS) of the rock, MPa.

It is recommended by HEAL et al [29] that the potential for rockburst damage can be captured through the use of the following five variables collected for each rockburst damage case history. There are the SCF, the GSSC, the ES, the GS and PPV at the rockburst site. Those indicators are recognized as the major parameters to quantitatively discover the activities in context of rockburst damage potential. Based on these considerations, these five variables (SCF, GSSC, ES, GS and PPV) are adopted as the input indicators for the prediction of rockburst damage in the SGB model. Numerous scholars such as KAISER et al [2], HEAL et al [29] and ZHOU et al [5] have conducted a variety of rockburst classification methods. In general, the division of rockburst damage can be described according to general damage characteristics of rockburst in burst-prone mines. The descriptions of the rockburst damage classification state are provided in Table 1 [3,29].

Table 1 Rockburst damage classification and its characteristics

3.3 Data sources and data description

To measure the performance of the developed SGB approaches, the data are collected by the ACG from the original work of HEAL [3] database. The details of these cases are presented in Table 2 which lists main parameters included in this database. The database contains data on 13 underground hard rock mines in Australia and Canada and composes of 254 cases of rockburst events.

Table 2 Descriptive statistics of input parameters for SGB modeling

Note that the GSSC and GS are dimensionless parameters and quantized as recommended by HEAL et al [29]. Consequently, the GSSC is classified as 2, 5, 8, 10 and 25 for the spot bolting (spacing > 1.5 m), pattern bolting (spacing 1-1.5 m), pattern bolting with a second bolting (overall spacing < 1 m), pattern bolting and pattern cable bolts and pattern dynamic support around the excavation, respectively. Similarly, the GS is also classified into three labels, the seismically active major structure is taken as 0.5, unfavorable rock mass/no major structure is taken as 1 and massive rock mass/no major structure around the excavation is taken as 1.5.

Fig. 4 Pie chart showing distribution of observed rockburst damage cases

Fig. 5 Pairs plot of observed rockbnrst damage cases for five parameters

The distribution of rockburst damage data is depicted in Fig. 4 as a pie chart illustrating the proportion of the four types of rockburst in burst prone mines, categorized as R2 (116 cases), R3 (48 cases), R4 (63 cases) and R5 (27 cases). Note that R1 is omitted from the original dataset because of the large number of very minor damage locations that are unreported/unnoticed during rockburst investigations [3]. The scatterplot matrix is shown in Fig. 5. The pairwise relationship is in lower panel, the correlation coefficient is in upper panel, and the marginal distribution for each parameter is on the diagonal. It can be seen that the parameter SCF is correlated with GSSC.

3.4 Development and validation of SGB model

The original dataset of rockburst with known classes is randomly divided into two subsets: a training set and an independent test set. Here, 205 data sets of 254 data sets (about 80% of the available data) are taken as training dataset, the reserved 49 data are considered as independent test dataset. Besides this, all input variables are scaled concerning the minimum and maximum of the data into the [0,1] range. The validation methods of model involves substitution method, holdout method, leave-one-out cross-validation (CV) method, leave more-out CV method and k-fold CV method [5,20,22]. On the other hand, as mentioned above, SGB classifier includes several parameters that have to be tuned. The train function from caret package within R [25] performs a grid of tuning parameters for a number of classification routines, which allows for a single consistent environment for training each of the SL algorithms and tuning their associated parameters. Here, several adjustable tuning parameters used by the SGB algorithm to optimize classification performance is examined using k-fold CV about computation time and variance, 10 folds is recommended by KOHAVI [37] when comparing the performance of machine learning algorithms [5]. Therefore, 10-fold CV procedure is applied for each possible parameter configuration during the construction of SGB model. In this procedure, the compounds of the training set are randomly divided into 10 subsets. Thus, each fold of cross validation randomly selects 10% of the data to serve as test data; then, the process fits a model on the remaining 90% of the data, as illustrated in Fig. 6. In each turn, a sample of data is partitioned into complementary subsets: the training set (white), and the test set (grey). These sets are employed to training and validation, respectively. By taking the mean of the results produced in each turn, an overall quality estimate can be provided. One ultimately finds that the model would minimize the prediction error averaged across all 10 folds and models. The independent test set is never used in the development of the SGB model but it is used to test the predictive power of the final model. Thus, the predictive model is constructed using selected variables and training set and applied to independent test set as demonstrated in Fig. 6.

4 Results and discussion

4.1 Result of 10-fold CV procedure

The SGB model is implemented with the caret [25] and gbm [26] R-packages in R software. To estimate rockburst damage, five indicators (PPV, SCF, ES, GSSC and GS) are adopted as input variables and the measured rockburst damage is chosen as an independent response variable in the developed SGB model. Classification tree [25] is used as the single classifier in SGB. The 10-fold CV procedure [5,20,22] is done to determine the optimal parameter values during modeling. A desired “tune length” variable can be passed to the “train” function in the caret package [25]. As described by KUHN and JOHNSON [19], the SGB has three tweaking parameters: M, v and J. To determine the optimal combination of these parameters in the interests of achieving the highest overall model accuracy during the CV process, a set of SGB models are tested using different values for v (0.001, 0.01, 0.05 and 0.1), J (1, 3, 5, …, 13, 15), and M (100, 150, 200, 250, …, 950, 1000). So, it will find one with the highest accuracy and Kappa and an optimal solution can be searched, as demonstrated in Fig. 7. The final values used for the SGB model are J = 1 and M = 300 when v = 0.1. The CAR and Kappa of the SGB model are found to be 53.00% and 0.285 for 205 sets of training data using 10 folds CV procedure.

4.2 Result of independent test set

To validate the predictive model based on the predicted and measured (real) values, 49 testing samples (Table 3) are validated by the proposed model. The CAR and Kappa of the SGB model are found to be 61.22% with 95% CI (46.24%, 74.80%) and 0.425 for 49 sets of testing data. As can be seen from Table 3, the results are identical with field observations and the accuracy of this SGB classification model is appropriate.

Further investigation of producer’s and user’s accuracies [20, 28] for each class using the SGB model is also calculated in Table 3. Therefore, producer’s and user’s accuracy performance measures for each class are calculated for the test set based on confusion matrices (Table 3). The producer’s and user’s accuracies indicate that some features are better classified than others. R₂ is classified more accurately compared with R₃ in SGB model. Also R₅ receives a relatively low user’s accuracy (less than 60.0%) in SGB model. It is evidence that the relationships between variables in rockburst events are almost always highly non-linear and extremely complicated.

Fig. 6 Illustration of overall procedure for performance evaluation for rockburst damage classification using SGB methods

Fig. 7 Tuning parameters for determining optimal model of SGB method

Table 3 Confusion matrices and associated classifier accuracies for SGB prediction model based on test set of rockburst damage

4.3 Relative importance of variables

The generic function varImp () in caret package can be used to characterize the general effect of predictors on the model [19]. Variables are sorted by average importance across the classes. For most classification models, each predictor will have a separate variable importance for each class, the default variable importance metric regards the area under the curve from a receiver operating characteristic analysis concerning each predictor, and is model independent [5]. In addition, all measures of importance are scaled to have a maximum value of 100. Figure 8 provides the result for the SGB model using function ‘‘varImp()” in the ‘‘caret” package [25] and displays the relative variable importance for each of the 15 predictor variables. Not surprisingly, PPV is the most sensitive factor among the indicators for the prediction of rockburst damage. The indicator SCF takes the second place of sensitivity. The indices of ES and GSSC are a bit sensitive, and the factor of GS is not as sensitive as the former two factors. The findings demonstrate that the SGB model is more sensitive to the indicator of PPV among the indicators for the prediction of rockburst damage in burst prone mines. The result is consistent with the correlation matrix of the variables that shows the highest coefficients for these variables (Fig. 5), and compares well with the previous research on this topic [2,3,7]. This also indicates that the selecting PPV as the main consideration of rockburst support is reasonable. This has been confirmed previously by KAISER et al [2], who proposed a support design rationale to resist rockburst damage and introduced PPV into an essential support design step.

Fig. 8 Ranking variable importance associated with rockburst damage classification evaluation by SGB method

4.4 Limitations

First, the limitation of the proposed model is that the number of dataset is relatively small. It should be calibrated by a larger dataset involved in SGB modeling to improve the model’s precision and reliability. Second, the predictive accuracy of SGB method is relatively low. Also, it is worth noting that the accuracy of rockburst damage prediction is, to a large extent, highly dependent on the quantity, quality and reliability of original dataset and the rationality of mathematical model. Alternatively, the most widely accepted explanation is that the SC may be overestimated and the PPV at the excavation boundary may be incorrectly measured due to its variations. Moreover, there may be additional indicators, theoretically, some seismic source parameters may be ignored because data collection is a massive challenge. Besides this, as pointed out by Refs. [5,20], major disadvantages of SGB are that there is a high sensitivity to the selection of the dataset with respect to the resulting tree structure, its “black box” nature that prohibits easy interpretation of the relationships between the response and predictor variables and the data are often overfitted.

5 Conclusions

1) Stress condition factor, the ground support system capacity, the excavation span, the geological structure and the PPV of rockburst sites are taken as the criterion indices for rockburst damage prediction in the SGB model. Ten-fold CV procedure is applied for each possible parameter configuration during the construction of SGB model. The findings reveal that SGB model for predicting rockburst damage can be a valuable tool for work in burst prone mines.

2) SGB model demonstrates that PPV is the most relevant predictor among the indicators for the prediction of rockburst damage classification. In future work, a larger dataset associated with other important parameters such as seismic source parameters can be calibrated in the SGB modeling to improve the model’s precision and reliability.

References

[1] ORTLEPP W D. RaSiM Comes of age—A review of the contribution to the understanding and control of mine rockbursts [C]//Controlling Seismic Risk—Proceedings of Sixth International Symposium on Rockburst and Seismicity in Mines. Nedlands: Australian Centre for Geomechanics, 2005: 3-20.

[2] KAISER P K, MCCREATH D R, TANNANT D D. Rockburst support handbook [M]. Canada: Geomechanics Research Centre, Laurentian University, 1996.

[3] HEAL D. Observations and analysis of incidences of rockburst damage in underground mines [D]. Perth: University of Western Australia, 2010.

[4] STACEY T R, ROJAS E. A potential method of containing rockburst damage and enhancing safety using a sacrificial layer [J]. Journal of the Southern African Institute of Mining and Metallurgy, 2013, 113(7): 565-573.

[5] ZHOU J, LI X B, MITRI H S. Classification of rockburst in underground projects: Comparison of ten supervised learning methods [J]. Journal of Computing in Civil Engineering, ASCE, 2016: 1-19.

[6] ORTLEPP W D, STACEY T R. Rockburst mechanisms in tunnels and shafts [J]. Tunnelling and Underground Space Technology, 1994, 9(1): 59-65.

[7] ZHOU J. Strainburst prediction and spalling depth estimation using supervised learning methods [D]. Changsha: Central South University, 2015. (in Chinese)

[8] ALBRECHT J, SHARROCK G. A model to forecast rockburst damage [C]//Challenges in Deep and High Stress Mining. Perth: Australian Centre for Geomechanics, 2006: 1-15.

[9] SHI X Z, ZHOU J, DONG L, HU H Y, WANG H Y, CHEN S R. Application of unascertained measurement model to prediction of classification of rockburst intensity [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(1): 2720-2726. (in Chinese)

[10] MITRI H S. Assessment of horizontal pillar burst in deep hard rock mines [J]. International Journal of Risk Assessment and Management, 2007, 7(5): 695-707.

[11] MITRI H S, TANG B, SIMON R. FE modelling of mining-induced energy release and storage rates [J]. The Journal of the South African Institute of Mining and Metallurgy, 1999, 99(2): 103-110.

[12] ZHOU J, LI X B, SHI X Z. Long-term prediction model of rockburst in underground openings using heuristic algorithms and support vector machines [J]. Safety Science, 2012, 50(4): 629-644.

[13] CASTRO L A M, BEWICK R P, CARTER T G. An overview of numerical modelling applied to deep mining [C]//Innovative Numerical Modeling in Geomechanics. London: Taylor & Francis Group, 2012: 393-414.

[14] WILES T D. Rockburst prediction using numerical modelling: Realistic limits for failure prediction accuracy [C]//6th International Symposium on Rockbursts and Seismicity in Mines (RaSiM 6). Perth: Australian Centre for Geomechanics, 2005: 57-63.

[15] CHEN D F, FENG X T, YANG C X, CHEN B R, QIU S L, XU D P. Neural network estimation of rockburst damage severity based on engineering cases [C]//Sinorock2013 Symposium. Shanghai: CRC Press, 2013: 457-462.

[16] ZHOU J, SHI, X Z, DONG L, HU H Y, WANG H Y. Fisher discriminant analysis model and its application for prediction of classification of rockburst in deep-buried long tunnel [J]. Journal of Coal Science and Engineering (China), 2010, 16(2): 144-149.

[17] DONG L J, LI X B, PENG K. Prediction of rockburst classification using Random Forest [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(2): 472-477.

[18] FRIEDMAN J H. Greedy function approximation: A gradient boosting machine [J]. Annals of Statistics, 2001, 29(5): 1189-1232.

[19] KUHN M, JOHNSON K. Applied predictive modeling [M]. New York: Springer, 2013.

[20] ZHOU J, LI X B, MITRI H S. Comparative performance of six supervised learning methods for the development of models of pillar stability [J]. Natural Hazards, 2015, 79(1): 291-316.

[21] BRILLANTE L, GAIOTTI F, LOVAT L, VINCENZI S, GIACOSA S, TORCHIO F, SEGADEC S R, ROLLEC L, TOMASI D. Investigating the use of gradient boosting machine, random forest and their ensemble to predict skin flavonoid content from berry physical–mechanical characteristics in wine grapes [J]. Computers and Electronics in Agriculture, 2015, 117: 186-193.

[22] ZHOU J, SHI X Z, LI X B. Utilizing gradient boosted machine for the prediction of damage to residential structures due to blasting vibrations of open pit mining [J]. Journal of Vibration and Control, 2015: 1-12.

[23] GODINHO S, GUIOMA N, GIL A. Using a stochastic gradient boosting algorithm to analyse the effectiveness of Landsat 8 data for montado land cover mapping: Application in southern Portugal [J]. International Journal of Applied Earth Observation and Geoinformation, 2016, 49: 151-162.

[24] YANG R M, ZHANG G L, LIU F, LU Y Y, YANG F, YANG F, YANG M, ZHAO Y G, LI D C. Comparison of boosted regression tree and random forest models for mapping topsoil organic carbon concentration in an alpine ecosystem [J]. Ecological Indicators, 2016, 60: 870-878.

[25] KUHN M. Building predictive models in R using the caret package [J]. Journal of Statistical Software, 2008, 28(5): 1-26.

[26] RIDGEWAY G. Generalized boosted models: A guide to the gbm package [EB/OL]. [2015-9-15]. http://cran.r-project.org/web/ packages/gbm/index.html, 2007.

[27] R DEVELOPMENT CORE TEAM. R: A language and environment for statistical computing [EB/OL]. [2015-9-15]. http://www.R- project.org/, 2014.

[28] CONGALTON R G, GREEN K. Assessing the accuracy of remotely sensed data: Principles and practices [M]. 2nd ed. Lewis: Boca Raton, FL, 2009.

[29] HEAL D, POTVIN Y, HUDYMA M. Evaluating rockburst damage potential in underground mining [C]//Proceedings of 41st U. S. Symposium on Rock Mechanics (USRMS). Golden: ARMA, 2006: 1020-1025.

[30] MISICH I, LANG A. Examples of rockburst damage in western australia [C]//Proceedings of the Fifth International Symposium on Rockburst and Seismicity in Mines (RaSiM5). Johannesburg: South African Institute of Mining and Metallurgy, 2001: 59-68.

[31] DURRHEIM R J, ROBERTS M K C, HAILE A T, HAGAN T O, JAGER A J, HANDLEY M F, SPOTTISWOODE S M, ORTLEPP W D. Factors influencing the severity of rockburst damage in South African gold mines [J]. The Journal of the South African Institute of Mining and Metallurgy, 1998, 98(2): 53-58.

[32] POTVIN Y. Strategies and tactics to control seismic risks in mines [J]. The Journal of the South African Institute of Mining and Metallurgy, 2009, 109(3): 177-186.

[33] HUDYMA M, POTVIN Y. An engineering approach to seismic risk management in hardrock mines [J]. Rock Mechanics and Rock Engineering, 2010, 43(6): 891-906.

[34] PAKALNIS R, VONGPAISAL S. Mine design—An empirical approach [C]//In Proceedings International Congress on Mine Design. Rotterdam: Balkema, 1993: 455-467.

[35] MCGARR A. A mechanism for high wall-rock velocities in rockbursts [J]. Pure and Applied Geophysics, 1997, 150(3-4): 381-391.

[36] QIU S L, FENG X T, ZHANG C Q, XIANG T B. Estimation of rockburst wall-rock velocity invoked by slab flexure sources in deep tunnels [J]. Canadian Geotechnical Journal, 2014, 51(5): 520-539.

[37] KOHAVI R. A study of cross-validation and bootstrap for accuracy estimation and model selection [C]//IJCAI-95, Proceedings of 14th International Joint Conference on Artificial Intelligence. San Francisco: Morgan Kaufmann Publishers Inc, 1995: 1137-1143.

随机梯度提升方法预测有岩爆倾向矿山岩爆破坏的可行性

周 健，史秀志，黄仁东，邱贤阳，陈 冲

中南大学 资源与安全工程学院，长沙 410083

摘  要：基于254个岩爆破坏事件数据库，采用随机梯度提升方法(SGB)对岩爆破坏进行分类检验评估。SGB方法中选取 5 个可能性相关指标进行评价，包括应力条件因素、地下支护能力、地质构造以及岩爆发生场地质点峰值振动速度等指标。模型在评价过程中选取80%的原始数据进行建模并使用10倍交叉验证方法评估模型的性能，然后进行外部测试，用剩余20%的数据检验SGB模型的预测准确性。对于多类问题模型准确性分析采用分类准确率和科恩Kappa系数两种准确性方法。对岩爆破坏的数据准确性分析和Kappa系数的分析表明SGB模型分析法对于岩爆破坏预测是可靠的。

关键词：有岩爆倾向矿山；岩爆破坏；随机梯度提升方法

(Edited by Mu-lan QIN)

Foundation item: Project (2015CX005) supported by the Innovation Driven Plan of Central South University of China; Project supported by the Sheng Hua Lie Ying Program of Central South University, China

Corresponding author: Ren-dong HUANG; Tel: +86-13135316968; Fax: +86-731-88879612; E-mail: HLA@csu.edu.cn

DOI: 10.1016/S1003-6326(16)64312-1