J. Cent. South Univ. (2017) 24: 1494-1502
DOI: 10.1007/s11771-017-3553-2
Model calibration concerning risk coefficients of driving safety field model
LI Yang(李洋)1, WANG Jian-qiang(王建强)2, WU Jian(吴剑)1
1. State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084, China;
2. Collaborative Innovation Center of Electric Vehicles in Beijing, Tsinghua University, Beijing 100084, China
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract:
Driving safety field (DSF) model has been proposed to represent comprehensive driving risk formed by interactions of driver-vehicle-road in mixed traffic environment. In this work, we establish an optimization model based on grey relation degree analysis to calibrate risk coefficients of DSF model. To solve the optimum solution, a genetic algorithm is employed. Finally, the DSF model is verified through a real-world driving experiment. Results show that the DSF model is consistent with driver’s hazard perception and more sensitive than TTC. Moreover, the proposed DSF model offers a novel way for criticality assessment and decision-making of advanced driver assistance systems and intelligent connected vehicles.
Key words:
1 Introduction
Road accidents have posed a serious threat to our daily life. There were 187781 traffic accidents and 58022 traffic fatalities in China in 2015, leading to a property loss of more than $150 million [1]. Intelligent connected vehicle is expected to be a promising solution to traffic accidents. Over the last decades, many collision warning/collision avoidance (CW/CA) technologies have been developed with the purpose of reducing traffic accidents [2-4]. Criticality assessment module, which evaluates the risk degree of driving condition, is the most important part of CW/CA systems [5]. The most popular criticality assessment measure is the simplest time measure, such as time to collision (TTC), time to brake (TTB) and time to steering (TTS) [6, 7]. Distance measure is also a widely-used measure for CW/CA algorithms of many car manufactures [2]. In addition, to consider environmental or behavioral uncertainties, collision probability-based criticality measure [8] or machine learning-based measure [9] are employed. However, heavy computational loads limit the applications of collision probability or data-driven method in real world driving. Therefore, since current criticality measures only consider vehicle dynamic or kinetic characteristics, it is hard to handle the potential driving risks formed by complex, continuous, uncertain, and dynamic environments. Recently, criticality assessment methods based on artificial potential field theory have been proposed [10-16].
Artificial potential field theory is firstly proposed for real-time obstacles avoidance for manipulators and mobile robots [11]. GERDES and ROSSETTER [12] employed the artificial potential field theory for vehicular stability control, making it easier for integration of various assistance systems, such as lane keeping and vehicle stability system. Requirements and important parameters for formulating the potential field function are discussed. However, the detailed form of the potential field is not proposed. MATSUMI et al [13] employed the potential field theory to develop a pedestrian collision avoidance system at un-signalized intersection. It is assumed that the destination point generates attractive force and the obstacle generates repulsive force on the vehicle respectively. It makes possible to detect the potential collision risk caused by environmental occlusions. However, it is necessary to conduct the real-world testing in complicated environments. RAKSINCHAROENSAK et al [14] proposed a motion planning and optimum control method for autonomous driving based on the potential field theory, but the real world experiment for method verification in the context of autonomous driving was not proposed. Recently, WANG et al [15] proposed a driving safety field (DSF) model based on potential field theory, which represents the comprehensive driving risk caused by human-vehicle-road interactions in the mixed traffic environment. Also, a collision avoidance algorithm based on DSF model has been presented [16]. However, there are many undetermined parameters involved in this model, which hamper the applicability of DSF model in the real-world environment. Thus, it is essential to propose a practical method to calibrate undetermined parameters. Generally, drivers would feel more or less stressed when perceiving driving risks. Since DSF model is established to describe the driving risk, there must be some connections between DSF model and human stress level. From this perspective, we expect to calibrate the DSF model based on driver stress level.
It is apparent that there would appear some vibrations in physiological signals when one feels stressed. Previous works have focused on connections between driver stress level and physiological signals [17-21]. There are some frequently-used physiological signals, such as Galvanic skin response (GSR) or called Electro dermal activation (EDA), electrocardiogram (ECG), respiration (RSP), blood volume pulse, electromyogram (EMG), skin temperature (SKT) and electroencephalogram (EEG) [17, 20, 21]. HEALEY et al [17] found that skin conductivity (GSR) and heart rate (ECG) metrics are most closely correlated with driver stress level compared with EMG and RSP through a real-world test of 24 drivers. LIN et al [18] studied driver’s distraction–related Electroencephalography (EEG) activities when facing with complicated tasks. Results showed that complex driving tasks would induce more event-related EEG activities, which could be used as a distraction index for early detection of driver inattention. Moreover, LIN et al [19] used electroencephalography (EEG) to detect drivers’ cognitive states in relation to their abilities in perception, recognition, and vehicle control. RIGAS et al [20] employed physiological signals to extract scenarios in which drivers felt stressed from a large amount of driving data. Physiological signals were calculated as features for classification and resulted in a detection accuracy of 82%. In all, physiological signals can reflect driver’s stress level when facing complex driving tasks.
This work proposes a feasible approach for risk coefficients calibration of DSF model based on driver stress level. A grey relation degree analysis and genetic algorithm is used. Results show that the proposed DSF model is consistent with driver stress level and more sensitive to potential collision risk than the simple TTC.
2 Concept of driving safety field model
DSF model is established to represent driving risks caused by interactions of driver-vehicle-road, which has been proposed in our previous research [15, 16]. The concept of DSF model is shown in Fig. 1. Driving risks in the traffic system are influenced by driver, vehicle and road factors. Driver factors include: physiology and psychology; cognition; driving skill and awareness of traffic rule. Vehicle factors, include vehicle type, mechanical performance, moving states and other road users (e.g. pedestrian, bicycle, tricycle), etc. Road factors include road adhesion coefficient, road slope, weather, no-moving objects and traffic rules, etc.
2.1 Driving safety field model
In this work, we modified the original DSF model for simplification. Here, we consider two traffic elements: obstacle (dynamic or static) and lane marker.
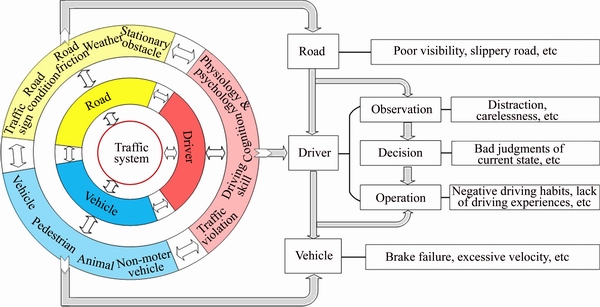
Fig. 1 Influencing factors of driving safety field [15]
2.1.1 Representation of obstacle
Compared with the previous research, collision possibility and collision severity are considered in the DSF model. If there is no possibility of collision, the potential field is considered to be zero. Each obstacle generates a longitudinal and lateral field force. A field force with larger magnitude indicates a higher driving risk. The coordinate of potential field is centered on mass center of vehicle, x-axis lines along the driving direction and y-axis is perpendicular to the driving direction. The field force formed by obstacle j at point (xj, yj) in longitudinal and lateral direction is denoted as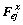 
and 
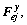respectively
(1)
where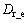 
denotes driver risk influencing factor; Re denotes road condition influencing factor; Mej denotes merged equivalent mass of the vehicle e and obstacle j; ve and vj are velocities of host vehicle and the obstacle respectively. The host vehicle center is (xe, ye), the relative distance vector rej=(xj-xe, yj-ye). The direction of field force Fej is exactly the same as that of rej, which is also the gradient descent direction of risk. In this model, k1, k2, k3 are undetermined risk coefficients which need to be calibrated.
The potential field of the obstacle is just like a hill that surrounds the obstacle, as shown in Fig. 2. The higher hill represents a higher driving risk. The range of the hill is determined by both the collision severity and criticality. If there is no collision, the potential field would become zero.
2.1.2 Representation of lane marker
The potential field of lane marker increases
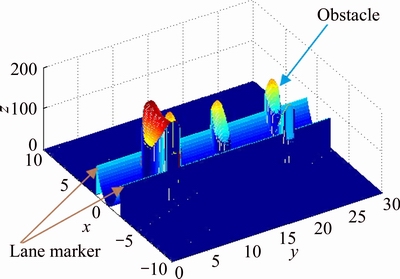
Fig. 2 Illustration of potential field of pedestrians and lane marker
dramatically when the host vehicle drifts towards the lanes. The minimum potential field of lane marker lies in the lane center, as illustrated in Fig. 2. Here, only lateral position of the vehicle is considered in the potential model with a form of Gaussian function [14]. The field force formed by lane marker L is denoted as Fel.
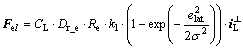(2)
where CL denotes the type of lane (e.g. solid, dotted, yellow, white, etc.); 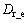denotes driver risk influencing factor; Re is road condition influencing factor; kl is the magnitude of field force when one of vehicle wheels overlap with the lane marker. The lateral offset of the vehicle center is denoted as elat; 
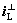denotes the direction that is perpendicular to road lane. The shape parameter of risk distribution is σ, which is determined by lane width. In this model, kl is an undermined parameter.
2.2 Model parameters of driving safety field
As discussed previously, there are four types of model parameters involved in the DSF model: 1) driver influencing factor 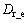; 2) road condition influencing factor Re; 3) merged equivalent mass Mej and 4) risk coefficients k1, k2, k3. The detailed explanations of each type of model parameters are shown as follows.
2.2.1 Driver influencing factor
Most accidents are caused by driver mistakes, so driver’s risky characteristics have a great influence on driving risks. Driver’s characteristics can be analyzed from four perspectives, including physiology and psychology level, cognition, driving skill and awareness of traffic rule. Therefore, driver influencing factor 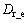is calculated as
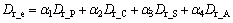(3)
where αi (i=1, 2, 3, 4) denote weights of four perspectives;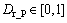 
denotes the driver’s physiology and psychology level; 
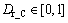denotes cognition capability;
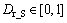denotes driving skill; 
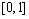denotes the awareness of traffic rule. Here, Dre is set as a scalar between 0 and 1. For simplification, the detailed calibration method for driver influencing factor is not considered in this work.
2.2.2 Road condition influencing factor
Similarly, risk characteristics of roads can be analyzed from four perspectives, including road adhesion coefficient μ, road curvature ρ, road slope τ and road visibility δ. Moreover, if the road section belongs to hazardous road sections with high frequency of accidents, the driving risk would increase. According to Ref. [22], the equivalent accident rate can be used to identify accidental road section using mass control method. Then, the road condition influence factor Re is formulated as
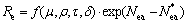(4)
where the equivalent accident number of one road section is Nea and its threshold is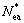 
, which are determined by historic traffic accidents of this road section. Similarly, how to calibrate the road condition influencing factor is not the focus of this work.
2.2.3 Merged equivalent mass
As discussed previously, the merged equivalent mass Mej represents the collision probability and potential collision severity if there occurs a collision. The collision probability is usually calculated as the integration of joint probability density function of states (e.g. position, pose, velocity, etc.) over the collision region [23] or the weighted sum of probability of trajectories which would lead to a collision [24]. Here, the potential collision severity is represented using the potential loss of energy of the collision entities. It is assumed that host vehicle and the obstacle collide in a line, according to the law of momentum conservation
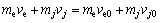(5)
where me and mj are mass of host vehicle and the obstacle; ve0 and vj0 denote initial speed of host vehicle and the obstacle before collision; ve and vj denote speed after the collision. Then, the potential energy loss Eloss can be written as
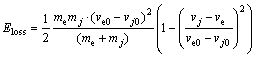(6)
Finally, Mej can be represented combining the collision probability Pcoll and potential collision severity Eloss as
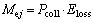(7)
It should be recognized that the merged equivalent mass Mej is formed by interactions of host vehicle and the obstacle.
2.2.4 Risk coefficients
Risk coefficients k1, k2 and k3 are essential parameters which determine the shape of the potential field. In Eq. (1), k1 denotes the weight of host vehicle speed; k2 denotes the weight of relative speed of host vehicle and obstacle; k3 denotes the exponent of relative distance. Therefore, to emphasize the importance of relative speed on driving risk, the weights are set as: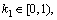 
k2=1. In addition, the exponent of denominator k3 is usually no more than three in order to avoid over-fitting.
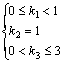(8)
Obviously, it is hard to calibrate all model parameter at one time. Therefore, we focus on calibration of risk coefficients of DSF model under the consumption that driver influencing factor, road condition influencing factor and merged equivalent mass are known. It should be noted that risk coefficients of DSF model are general model parameters which do not vary with individual characteristics of drivers. This is exactly the intrinsic difference between driver influencing factor and risk coefficients.
3 Calibration method of driving safety field model
As discussed previously, we only focus on the calibration of risk coefficients of DSF model in this work. Drivers would usually feel stressed when perceiving driving risks, so we expect to calibrate the risk coefficients of DSF model based on driver stress level.
3.1 Driver stress level
It is proved that skin conductivity and heart rate are most correlated with driver stress level [17]. Thus, driver’s stress level is written as combination of physiological signals include galvanic skin response (GSR) and heart rate (HR),
(9)
where Hstresslevel denotes driver stress level;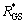 
and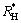 
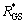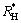are Galvanic skin response (GSR) and Heart rate (HR) signals, which are normalized between 0 and 1, and Wgsr, Whr are weights of and , respectively.
3.2 Grey relation analysis
Grey relation analysis is effective in addressing decision-making issues with multiple attributes and uncertainties by measuring the grey relation degree of each candidate solution to an optimum solution [25, 26]. To measure the consistency of driving safety model and driver stress level, grey relation analysis is employed is this study. However, grey relation analysis theory proposed by DENG [25] is easily affected by means of data normalization, which may contribute to biased results. This study employed a modified grey slope relation analysis method, which is capable of maintaining the order of original sequences after normalization.
A higher grey relation degree denotes more similarity to the reference sequence. In this study, we aim to maximize the grey relation degree between driver stress level and the proposed DSF model. Here, the driver stress level is used as the reference sequence, the driving safety model, time to collision (TTC), time headway (THW), hazard perception, differential TTC and THW are used as comparative sequences respectively. The reference sequence is denoted as X0={x0(1) x0(2) … x0(N)} and the comparative sequences are denoted as Xi={xi(1) xi(2) … xi(N)}, i=1, 2, …, M. There are several main steps for grey slope relation analysis as follows.
Step 1: Decision matrix X
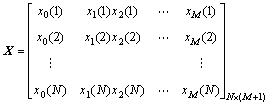(10)
Step 2: Slope matrix X′
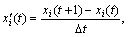i=1, 2, …, M; t=1, 2, …, N-1(11)
where △t=1.
Step 3: Normalized matrix X*
(12)
Step 4: Distance Δoi(t) between reference sequence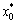 
and comparative sequences 
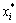is
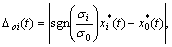i=1, 2, …, M; t=1, 2, …, N (13)
where σi is calculated as follows:
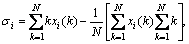i=1, 2, …, M (14)
Step 5: Calculate the grey relation degree γ(x0, xi) between sequence xi and sequence x0
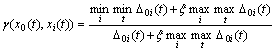(15)
where ξ denotes the distinguishing coefficient which is set as 0.5 for moderate distinguish effects and good stability [28].
3.3 Optimization model
DSF model is expected to change in a similar style to driver stress level. Risk coefficients k1, k2, k3 are undetermined parameters of DSF model. Thus, we aim to optimize risk coefficients for highest grey relation degree between driver stress level and DSF model. As such, the optimization model can be formulated as
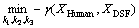(16)
where γ(XHuman, XDSF) denotes the grey relation degree between driver stress level XHuman and DSF model XDSF.
3.4 Genetic algorithm
Genetic algorithm (GA) is a meta-heuristic inspired by the process of natural selection and evolution, which is widely-used in computer science and operations research. It generates globally-optimum solutions by employing bio-inspired operators such as crossover, mutation and selection. GA has been successfully used in calibrating a conceptual rainfall-runoff model, which is proved to be effective and robust. WANG et al [22] employed the GA to calibrate the General Motors-based car following model in traffic research. As such, genetic algorithm is employed to parameter calibration of DSF model in this work. As shown in the Fig. 3, GA algorithm aims to optimize risk coefficients k1, k2 and k3 of DSF model to maximum the fitness function (grey relation degree). The initial population is set as the initial values of k1, k2 and k3. If average relative changes in the best fitness satisfy stop criterions, the algorithm would stop and output the optimum solution. If not, the populations would be operated using crossover, mutation and selection so as to create new populations and repeat the process.
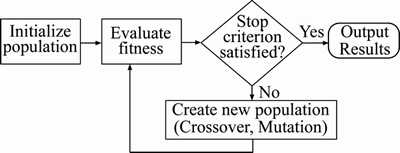
Fig. 3 Flowchart of genetic algorithm
4 Results
After the DSF model parameters are optimized using the genetic algorithm, a real-world field operational test is conducted to validate the effectiveness of the driving safety field model.
4.1 Field operational test
Three experiment vehicles are instrumented for test, as shown in Fig. 4. Each vehicle is equipped with GPS to collect position and time which can be used for data synchronization. There are 24 normal drivers recruited to participate the test, including 20 male drivers and 4 female drivers. The average age is 36.5 (standard deviation is 9.6). Each driver held a valid driver’s licenses for an average of 11 years (standard deviation is 6.9 years). GSR and HR signals were measured using EDA and PPG sensor in the test respectively, as shown in Fig. 4.
Fig. 4 Experiment vehicles [16]
Fig. 5 EDA (a) and PPG (b) sensors for measuring GSR and HR signals
4.2 Model solution
As discussed previously, the genetic algorithm is used for parameters optimization. The parameter of GA is set as follows: 1) Float encoding method is used. The initial population size is 20 and there are 30 generations in total; 2) Crossover and mutation are used to generate new populations. The selection function is roulette. The crossover is two points with crossover rate of 0.8 and the mutation is set as adaptively-feasible; 3) Fitness function is the objective function of optimization model and 4) Risk coefficients of DSF model parameters are set as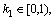 
k2=1 and 
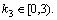If the average relative change in the best fitness function value is less than 1×10-6, the algorithm would stop. As shown in Fig. 6,the fitness value quickly converged after four generations and the objective function is -0.973. Finally, the optimized model parameters are set as: k1=0, k2=1, k3=3.
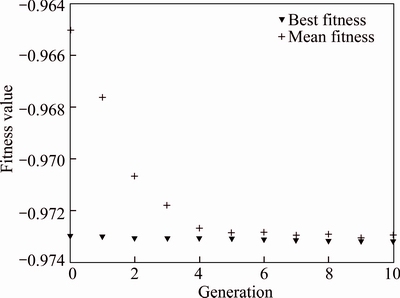
Fig. 6 Iteration process of genetic algorithm
4.3 Model validation
Since TTC is the most common criticality assessment measure, TTC is used to test the effectiveness of the DSF model. Here, to avoid the situation in which the relative speed becomes zero and TTC becomes infinite, the reciprocal value of TTC (VTTCi) is used. The increase of VTTCi (unit: s-1) indicates the rise of driving risks. The negative value of VTTCi indicates no driving risks. Moreover, driver (human) stress level and brake signal are employed to show the dynamic change of the driving situations. For simplification, a typical car following scenario and cut-in scenario are extracted for model validation.
4.3.1 Car following scenario
The time trajectory of human stress level, risk field (DSF model), VTTCi (reciprocal value of TTC) and brake signal in a typical car following scenario are illustrated in Fig. 7. Driver’s stress level surges from 15 s to 25 s, signifying that the driver was stressed during this period. As a response, driver applied a braking since 12 s. As the increase of VTTCi usually indicates rise of driving risk, there did exist a potential driving risk which was reduced later by braking. It can be seen that driving risk field changes in a similar way as VTTCi. Moreover, risk field changes faster than VTTCi, showing that risk field is more sensitive to the driving risk than TTC measure.
4.3.2 Cut-in scenario
The time trajectory of human stress level, risk field (DSF model), VTTCi (reciprocal value of TTC) and brake signal in a cut-in scenario is shown in Fig. 8. Driver’s stress level goes up and reaches a highest point at 15 s. During the period from 13 s to 20 s, driver’s stress level maintains a higher level that is more than an average level (about 0.25). Simultaneously, driver applies braking over this period. Both VTTCi and risk field can detect the collision risk at 15 s correctly. The direction of risk field is nearly 60° at about 19 s, indicating a cut-in collision risk, as shown in Fig. 9. Therefore, it can be concluded that risk field is more effective than TTC in detecting collision risk caused by cut-in vehicles.
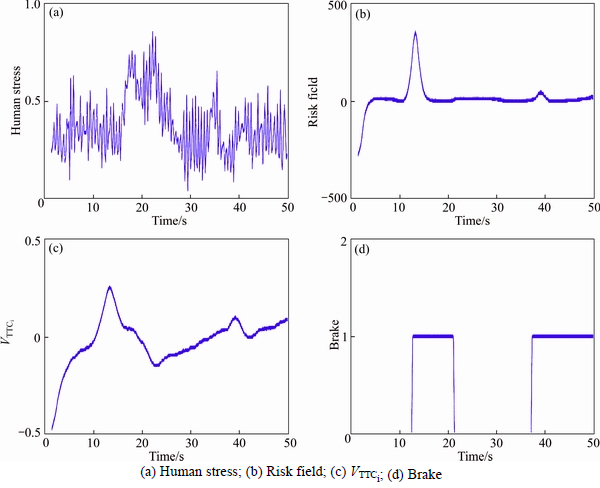
Fig. 7 Driver safety field model validation in car following scenario:
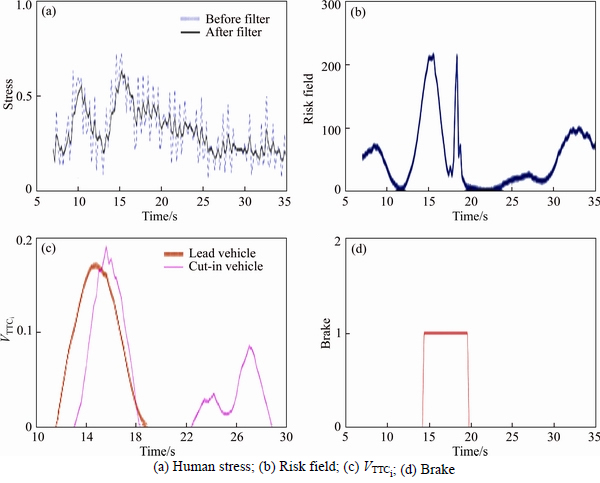
Fig. 8 Driver safety field model validation in cut-in scenario:
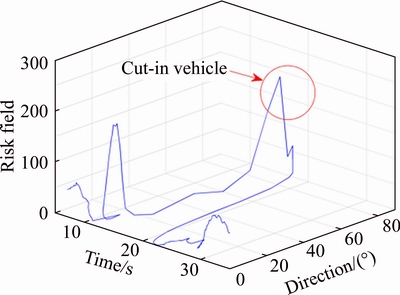
Fig. 9 Driving safety field and its direction changes with time
5 Discussions and conclusions
This work proposes a reasonable approach to calibrate risk coefficients of driving safety field model based on driver physiological signals. Also, driving safety field model is modified so as to consider the collision probability and potential collision severity. To search for the optimum risk coefficients, an optimization model is established based on grey slope relation degree analysis and solved using the genetic algorithm. A real-world driving experiment is finally conducted to validate the effectiveness of DSF model. Results show that DSF model is consistent with driver’s perception towards impending collision risks. Moreover, it is proved that driving safety field model is more sensitive than TTC especially for the unexpected cut-in scenario. In all, due to more considerations on the complicated interactions of driver-vehicle-road, driving safety field model is capable of improving adaptability to driver characteristics and aware of potential collision risks in an early stage compared with conventional collision avoidance technologies.
However, a few topics remain worth investigation to further reinforce the proposed DSF model. First, since there are so many unknown parameters, this work focuses on calibration of risk coefficients of DSF model. Remaining model parameters, such as driver influencing factor, road condition influencing factor, merged equivalent mass would be calibrated in the future researches. Next, to enhance the applicability and usefulness of DSF model in complex and dynamic environment, more typical and complicated scenarios are needed to be analyzed. Third, we will continue to improve the model contracture and propose a general form of driving safety field model that applies to all conditions. As a whole, the proposed DSF model is expected to offer a novel way for criticality assessment and decision making for future intelligent connected vehicles.
References
[1] Traffic Administration Bureau of the Ministry of Public Security of P. R. China. China road traffic accidents statistics [R]. Beijing, China: Traffic Administration Bureau of the Ministry of Public Security of P.R. China, 2015. (in Chinese)
[2] LEE K, PENG H. Evaluation of automotive forward collision warning and collision avoidance algorithms [J].Vehicle System Dynamics, 2005, 43(10): 735-751.
[3] FILDES B, KEALL M, BOS N, LIE A, PAGE Y, PASTOR C. Effectiveness of low speed autonomous emergency braking in real-world rear-end crashes [J]. Accident Analysis & Prevention, 2015, 81: 24-29.
[4] KUSANO K, GABLER H. Safety benefits of forward collision warning, brake assist, and autonomous braking systems in rear-end collisions [J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(4): 1546-1555.
[5] 
A, BONNIFAIT P, CHERFAOUI V. Risk assessment for collision avoidance systems [C]// Intelligent Transportation Systems (ITSC), 2014 IEEE 17th International Conference on, Qingdao, China: ITSC, 2014: 386-391.
[6] HILLENBRAND J, SPIEKER A, KROSCHEL K. A multilevel collision mitigation approach—its situation assessment, decision making, and performance tradeoffs [J]. IEEE Transactions on Intelligent Transportation Systems, 2006, 7(4): 528-540.
[7] KAEMPCHEN N, SCHIELE B, DIETMAYER K. Situation assessment of an autonomous emergency brake for arbitrary vehicle-to-vehicle collision scenarios [J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(4): 678-687.
[8] ALTHOFF M, STURSBERG O, BUSS M. Model-based probabilistic collision detection in autonomous driving [J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(2): 299-310.
[9] CHEN C, SEFF A, KORNHAUSER A, XIAO J. Deepdriving: Learning affordance for direct perception in autonomous driving [C]// Proceedings of the IEEE International Conference on Computer Vision, Santiage, Chile: IEEE, 2015: 2722-2730.
[10] REICHARDT D, SHICK J. Collision avoidance in dynamic environments applied to autonomous vehicle guidance on the motorway [C]// Intelligent Vehicles' 94 Symposium Paris, France: IVS, 1994: 74-78.
[11] KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots [J]. The International Journal of Robotics Research, 1986, 5(1): 90-98.
[12] GERDES J, ROSSETTER J. A unified approach to driver assistance systems based on artificial potential fields [J]. Journal of Dynamic Systems, Measurement, and Control, 2001, 123(3): 431-438.
[13] MATSUMI R, RAKSINCHAROENSAK P, NAGAI M. Autonomous braking control system for pedestrian collision avoidance by using potential field [J]. IFAC Proceedings Volumes, 2013, 46(21): 328-334.
[14] RAKSINCHAROENSAK P, HASEGAWA T, NAGAI M. Motion planning and control of autonomous driving intelligence system based on risk potential optimization framework [J]. International Journal of Automotive Engineering, 2016, 7: 53-60.
[15] WANG J, WU J, LI Y. The driving safety field based on driver–vehicle–road interactions [J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(4): 2203-2214.
[16] WANG J, WU J, ZHENG X, NI D, LI K. Driving safety field theory modeling and its application in pre-collision warning system [J]. Transportation Research Part C: Emerging Technologies, 2016, 72: 306-324.
[17] HEALEY J, PICARD R. Detecting stress during real-world driving tasks using physiological sensors [J]. IEEE Transactions on Intelligent Transportation Systems, 2005, 6(2): 156-166.
[18] LIN C, LIN H, CHIU T, CHAO C, CHEN Y, LIANG S, KO L. Distraction-related EEG dynamics in virtual reality driving simulation [C]// 2008 IEEE International Symposium on Circuits and Systems, Seattle, USA: IEEE, 2008: 1088-1091.
[19] LIN C, CHANG C, LIN B, HUNG S, CHAO C, WANG I. A real-time wireless brain–computer interface system for drowsiness detection [J]. IEEE Transactions on Biomedical Circuits and Systems, 2010, 4(4): 214-222.
[20] RIGAS G, GOLETSIS Y, FOTIADIS D. I. Real-time driver’s stress event detection [J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(1): 221-234.
[21] REBOLLEDO-MENDEZ G, REYES A, PASZKOWICZ S, DOMINGO M, SKRYPCHUK L. Developing a body sensor network to detect emotions during driving [J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(4): 1850-1854.
[22] ZHANG C, MA R. Identifying method of traffic accident black spots on mountain freeway [J]. Journal of Chang’an University: Natural Science Edition, 2010, 30(6): 76-80. (in Chinese)
[23] SCHREIER M, WILLERT V, ADAMY J. An integrated approach to maneuver-based trajectory prediction and criticality assessment in arbitrary road environments [J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(10): 2751-2766.
[24] LAUGIER C, PAROMTCHIK I, PERROLLAZ M, MAO Y. Probabilistic analysis of dynamic scenes and collision risks assessment to improve driving safety [J]. IEEE Intelligent Transportation Systems Magazine, 2011, 3(4): 4-19.
[25] DENG J. Control problems of grey systems [J]. Systems and Control Letters, 1982, 1(5): 288-294.
[26] ZHAI L, KHOO L, ZHONG Z. Design concept evaluation in product development using rough sets and grey relation analysis [J]. Expert Systems with Applications, 2009, 36(3): 7072-7079.
[27] CHANG T, WEN K, CHANG H, YOU M. A new method for evaluation of design alternatives based on the fuzzy gray relational analysis [C]// Fuzzy Systems Conference Proceedings, Seoul, Korea: FCCP, 1999: 708-713.
(Edited by DENG Lü-xiang)
Cite this article as:
LI Yang, WANG Jian-qiang, WU Jian. Model calibration concerning risk coefficients of driving safety field model [J]. Journal of Central South University, 2017, 24(6): 1494-1502.
DOI:https://dx.doi.org/10.1007/s11771-017-3553-2Foundation item: Projects(51475254, 51625503) supported by the National Natural Science Foundation of China; Project(MCM20150302) supported by the Joint Project of Tsinghua and China Mobile, China; Project supported by the joint Project of Tsinghua and Daimler Greater China Ltd., Beijing, China
Received date: 2016-12-15; Accepted date: 2017-04-01
Corresponding author: WANG Jian-qiang, PhD, Professor; Tel: +86-13520933903; E-mail: wjqlws@tsinghua.edu.cn
Abstract: Driving safety field (DSF) model has been proposed to represent comprehensive driving risk formed by interactions of driver-vehicle-road in mixed traffic environment. In this work, we establish an optimization model based on grey relation degree analysis to calibrate risk coefficients of DSF model. To solve the optimum solution, a genetic algorithm is employed. Finally, the DSF model is verified through a real-world driving experiment. Results show that the DSF model is consistent with driver’s hazard perception and more sensitive than TTC. Moreover, the proposed DSF model offers a novel way for criticality assessment and decision-making of advanced driver assistance systems and intelligent connected vehicles.
