目录结构

对钯氢体系的物理化学性质进行了综合评述。钯是一种面心立方 (fcc) 结构的吸氢金属 , 氢原子溶解在晶格中 , 占据八面体间隙位 (O) , 形成fcc的子晶格 , 吸氢时晶格发生等方性膨胀 ;氢在钯中的扩散路径为O T O跃迁 , 存在反同位素效应 ;钯氢化物的氢同位素分离因子较大 , 并受到温度、氢浓度等因数的影响 ;钯氢体系的p c等温线表现出良好的坪台性 , Pd H和Pd D均存在临界点 , 尚未确定Pd T有无临界点 ;单晶钯氢反应动力学与不同的晶面有关 ;钯氚体系存在氚老化效应

关键词：

钯;氢同位素;金属氢化物;

中图分类号： O614

收稿日期：2002-01-21

Physical and Chemical Properties for Palladium-Hydrogen System

Abstract：

The physical and chemical properties for Pd H system were reviewed. The crystal structure of pure Pd is of face centered cubic ( fcc ) and it is a hydrogen absorbing metal. The hydrogen atom dissolves in lattice and occupies octahedral interstitial position, and then forms hydrogen sublattice (fcc ) . Upon hydrogen absorption the lattice undergoes an isotropic expansion while retaining its fcc structure. The defects in lattice are mainly extended type. The diffusion path of hydrogen is O T O jumping and there is reverse isotopic effect accompanying with quantum effect. The separation factor of palladium hydride is relatively larger than other common metal hydride and is affected by temperature and hydrogen concentration. The pressure composition isotherm in palladium hydrogen system exhibits good plateau. Pd H and Pd D systems have their own critical point respectively, but it has not been in agreement about the critical point of Pd T system. The dynamical property for single crystal Pd H reaction associates with the specific crystal face exposured to hydrogen. Tritium aging effect exists in Pd T system.

Keyword：

palladium; hydrogen isotope; metal hydride;

Received： 2002-01-21

对金属中氢的研究已有很长的历史。早在1866年Graham就已发现大量氢气可溶解于过渡金属钯并于1868年首次开发出钯半透膜以净化氢气。金属Pd及其一些合金, 如Pd-Ag, Pd-Al等, 由于其氢化物的同位素效应显著, 在氚工艺与氢同位素生产中占据重要的地位, 常被用作氢同位素分离、纯化处理工艺的首选材料, 因此了解钯氢化物的物理化学性质对基础研究和工程应用研究具有重要意义。钯-氢体系除具有金属-氢体系的一般性质外, 还具有其独特的物理化学性质, 如氢的渗透性高、易氢化以及分离因子大等性质。本文重点评述了钯-氢体系的晶体结构、氢的扩散、氢的溶解热动力学、同位素效应等物化性质的研究现状。

1 Pd氢化物的结构及结合状态

1.1 Pd氢化物的结构

Pd晶体属面心立方 (fcc) 结构, 每个单胞含4个Pd原子, 4个八面体填隙位以及8个四面体填隙位 (T) 。晶格参数a₀为0.3890 nm (298 K) , 吸氢时晶格发生等方性膨胀, 但始终保持fcc结构。在稀释相 (α相) 区域, 298 K时PdH_x的a₀为0.3894 nm, 对应的氢含量H/Pd≈0.015。氕化物中α与β相共存区的a₀是0.4025 nm, 当p_H₂=0.1 MPa, H/Pd≈0.7时, a₀=0.4040 nm。在单一β相氕化物中的晶格膨胀将更大 ^[1] 。对于Pd-D在氢含量相同时, 膨胀会小一些 ^[2,3] 。两种相中的H原子均是无序的。

后来发现体系中存在有序低温相, 因此相图比简单的气-液型相图更复杂 ^[4,5,6,7] (图1) 。 Rush等 ^[8] 确定了低氕含量 (如H/Pd=0.002) 的光学波振动频率, 表明此时H-H相互作用的影响并不显著。氕在α相中的Einstein温度是801 K, 氘的Einstein温度是540 K, 于是给出θ_H/θ_D=1.49而非预想的。 β相中氕和氘的θ分别是685和460 K ^[9] ; 这表明α与β相的光学波均存在非简谐振动。但应注意, θ_{H (D)}明显依赖于Pd中的氢含量, 因为β相保持着与α相同的结构。

1.2 Pd-H结合状态

总能计算的结果给出了Pd-H体系中相当完整的结合图象。 (1) 氢加入Pd时, 少量的电荷从相邻Pd原子区域传输到相邻Pd和H原子区域。由于H的1s轨道和Pd的4d轨道之间的相互作用产生了新的结合状态 (比s-d结合低几个eV) 。 Pd原子周围的电荷是象d电子, 而H原子周围的电荷则象s电子, 两个位置周围的电荷数量相当; (2) Pd-H间的有效作用是短距离的, 几乎不超过最近邻的Pd原子; (3) 与H电子的杂化改变了4d电子的状态密度, 使之变窄, 包含的电子态变少, 并且它的重心向高结合能方向移动 (即增加了d 带填充) , 以致于损失了结合力; (4) 随着Fermi能级的电子态密度减小, Fermi能增加;。 (5) 严格的能带近似是无效的, 因为只有一小部分由额外H原子提供的电子位于导带顶部。

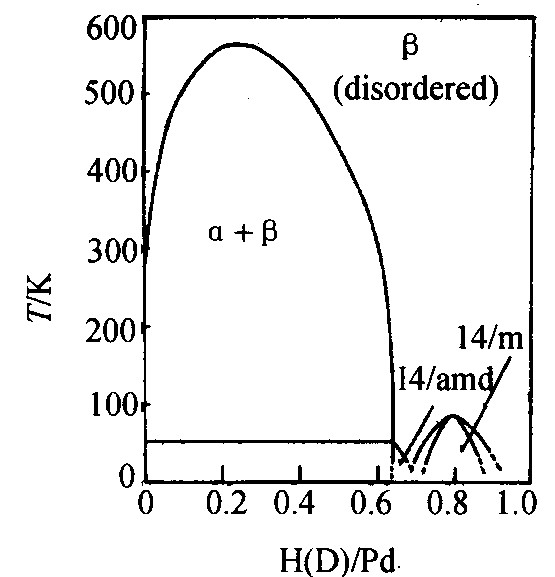
图1 Pd-H (D) 体系相图

Fig.1 Phase diagram of Pd-H (D) system

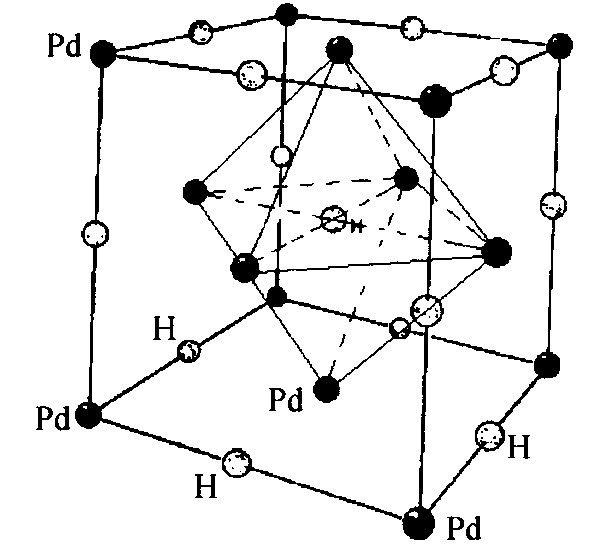
图2 H (或D) 原子在β相Pd-H (或Pd-D) 中的位置模型

Fig.2 Position modeling of H and D atoms in Pd lattice for β-phase Pd-H (D)

1.3 氢在β相钯氢化物中的位置

钯-氢体系多年来一直引起人们的兴趣, 主要是因为气体原子在金属中非同寻常的扩散特性。 Davis ^[10] 的扩散实验认为氢原子占据了Pd晶格的四面体位置。 X衍射研究表明, 根据氢含量不同, 体系中存在两种不同的fcc结构相。 Worsham等 ^[11] 利用中子衍射技术研究了氕和氘原子在Pd-H和Pd-D体系的α与β相中的位置。实验结果表明β相中的气体原子是位于晶格的八面体位置, 即O位 (如图2所示) 。这与Davis预测的不一致。 Worsham未能成功确定α相中氕、氘的位置, 因为在室温下只有非常少的气体进入该相。

2 氢在钯中的溶解

2.1 氢在钯中溶解的理论概述

在金属中氢的不同物理性质中, 溶解度是一个极其重要的性质。氢同位素 (H, D, T) 在钯中的溶解行为是类似的, 均表现为解离吸附溶解。但是由于H, D, T在气相与Pd晶格中的零点能和振动能不同, 它们在钯中的溶解度表现出明显的同位素效应。 L sser等 ^[12] 给出了氢在钯中的溶解理论, 阐述了气相氢与溶解在钯中的氢之间的平衡, 根据氢在气、固两相的化学势相等, 并将溶解在Pd晶格中的氢作为简谐近似, 忽略电子能效应的作用, 结合统计力学方法, 给出了金属中氢的偏摩尔Gibbs自由能和气态氢的标准Gibbs自由能以及平衡常数、偏摩尔焓、偏摩尔熵的解析表达式。由此可理论计算钯-氢体系的p-c等温线、热力学函数以及同位素分离因子等热力学性质。

2.2 氢在钯中的溶解度的影响因素

2.2.1 应力对氢溶解度的影响

流体静力学应力对填隙溶解度的影响已由Li等 ^[13] 研究, 并由Wriedt等 ^[14] 利用Pd-Ag合金证实。后来Kirchheim报道了在Pd上也存在同样的效果 ^[15] 。基本结论是金属中氢的化学势因所加流体学应力而发生变化:

对单轴向应力, 方程还原成Δμ_H=1/3V_Hσ_x。此方程也可作为获得V_H的替代方法。 V_H为H在浓缩相的偏摩尔体积。应力也可以是内应力, 尽管此时它们不易被确定。例如, 因为氚衰变在Pd中形成高压³He泡 ^[16] , 导致内应力场增加, 从而影响氢的溶解度 ^[17] 。

2.2.2 缺陷的作用

在充分退火的Pd中, 最初稀释相氢的溶解度遵守Sieverts定律, 即p^1/2-r图是线性的, 且当r趋于0时具有切线与原点相交的特征。实际的偏差必然是由于缺陷的存在。对氢溶解度存在影响的缺陷类型是普遍存在于金属中的缺陷, 例如点缺陷 (空位和杂质原子) 和扩展缺陷 (位错, 晶界, 外表面) 。

氢在α相Pd中的溶解度增加类似于冷处理使得位错应力场增加 ^[18,19] 。 Lynch等 ^[20] 认为, 已经过氢化物相变的样品氢溶解度增加类似于经强化冷处理后的结果, 可以认为它们的位错密度相当。冷处理与氢化循环后的Pd的性质之间的唯一差别是, 后者表现出沿H/Pd轴更大的非零相交, 并且这些样品在坪台压力到达前就会形成氢化物相。这被认为是在后者相变时内部存在少量的拉伸应力区 ^[21] , 该区域的氢化学势减小, 结果使得体系容易向氢化物转变, 即在较低的压力下, 就会导致α/ (α+β) 相界处的转变更圆滑而不是更尖锐, 正如在充分退火的Pd中所发现的结果一样。

Kirchheim ^[19,22] 和Bohmholdt ^[23] 定量描述了氢与位错边界的相互作用。除数量级之外, 很难得到确切的结果, 因为存在以下的不确定性: 位错中心的作用, 氢化物是否连续形成, 是否在这些位置全部形成氢化物相, 以及Q-Q相互作用的影响。

3 氢在钯金属中的扩散

从微观来看, 扩散系数可由平衡位置间的跃迁表示, 即:

D=f_Ta²/6τ_d (2)

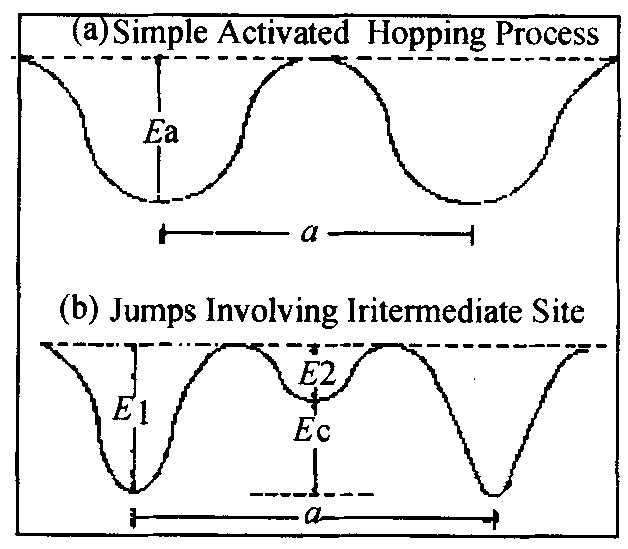
式中a为平均跃迁距离, τ_d为两次跃迁之间的平均时间, f_T是校正因子。图3 (a) 给出了涉及从势阱底直接跃迁的理想扩散。 E_a是扩散活化能且满足Arrhenius公式:

D=D₀exp (-E_a/k_BT) (3)

但实际证明氢的运动要复杂得多。图3 (b) 给出了一种可能的跃迁方式, 此时观察到的E_a与势阱深度是不一致的。与其它填隙原子 (如N, O, C) 相比, H原子在金属氢化物中的运动是相当快的, 观察到的室温扩散系数D值范围在～10^-16和～10^-6 cm²·s^-1之间。

图3 扩散过程中氢同位素的势阱示意图

Fig.3 Sketch diagram of potential well of hydrogen isotopes during diffusion

3.1 扩散实验结果

钯-氢体系中的扩散系数已被不同的方法确定。包括渗透、氢吸收、 Gorsky技术、准弹性中子散射 (QNS) 以及对稀释钯铁磁合金的退磁方法。

298 K时, 氢在Pd中的扩散系数相对较大, 当氢的含量很小时, 氕和氘在Pd 中的Einstein扩散系数分别为:

D^*_H=2.5×10^-7exp (-21.8 kJ/RT·x_H) m²·s^-1 (4)

D^*_D=1.7×10^-7exp (-19.9 kJ/RT·x_H) m²·s^-1 (5)

298 K时, H和D的扩散系数分别为3.8×10^-11和5.5×10^-11 m²·s^-1。尽管对H而言指前因子更大, 但D的扩散系数却比H大; H和D的扩散活化能之间的差异解释了D扩散更快。 Bohmholdt等 ^[23] 认为至少在室温或以上时, 扩散过渡态是四面体间隙位, 氢在此处的振动频率大于八面体位置, 所以零点能对过渡态的贡献将有利于重同位素扩散。

非理想状态下氢的Fick扩散系数D (r) 值是有实际价值的, 在298 K时, β相中的数值比在稀释相大约4.5倍 ^[23] 。 Fick扩散系数可表示为:

式中r是H/Pd原子比, D^*为Einstein扩散系数 (与浓度无关) , a为氢的活度, μ_H可由p_H₂得到:

3.2 氢在钯中扩散的模拟模型

Gillan ^[24] 用100个Pd原子和8个H原子进行了Pd-H体系中H扩散的MD (molecular dynamics) 模拟, 结果发现H最容易的扩散路径是O-T-O, 伴随T-O位能量差值 (即代表活化能) , D₀值与实验值一致。但模拟的结果与QNS实验数据不吻合, QNS数据与Chudley-Elliott (CE) 模型一致, CE模型是以不相关 (统计独立) 跃迁为基础。 Gillan认为这种矛盾不是因为所选用原子间势能造成的, 而应归于O位间的跃迁是相关的。 Culvahouse等 ^[25] 由统计分析表明大多数跃迁实际上是不相关的最近邻位置间的跃迁, 但跃迁时间分布绝对不是指数形式, 这就会增加非CE特性。同时发现与CE模型不一致的程度对所采用的Pd-H势能更为敏感, 选择更强的势能可使之更吻合; 在计算同一体系中H-H相互作用能也存在类似敏感性。

Salomons ^[26] 也采用了Gillan的原子间相互作用势能并计算出O-T位能量差为0.295eV。该数值被用于均域格子气体模型计算以获得H占据O与T位的分数: 600K以下H占据T位的分数可以忽略 (与实验结果吻合) , 与MD模拟中的数据一致。

4 钯-氢体系的热力学性质

4.1 Pd-Q体系相图

Pd-Q最典型的性质是在临界点以下出现两种固相 (见图1) , 钯-氢体系的临界点见表1。 Pd-T是否存在临界点尚存争论, 其原因可能在于氚的危险性限制了实验测定的实现。

多年来一直认为相图的混溶带组成了完整的相图, 尽管这与热力学第三定律所要求的规律 (当T→0时, 无序将消失) 矛盾。 1978年Ross等 ^[7] 用中子衍射反映了该体系的低温有序相 (见图1) 。

4.2 Pd-Q反应热力学的实验结果

Pd-H体系对热力学研究而言是方便的, 因为氢的化学位可容易地由氢气压力确定, 氢气压力与含氢金属相平衡。从实验确定的等温线可得到μ_H, 从μ_H=0.5RTlnp_H₂随温度的变化, 可得到相关的偏摩尔焓和偏摩尔熵, 即ΔH_H和ΔS_H。对于氢气在单相区吸收, 方程 (8) , (9) 可用:

(?lnp^1/2/? (1/T) ) _r=ΔH_H/R (8)

T (?lnp^1/2/?T) _r+lnp^1/2=-ΔS_H/R (9)

在两固相处于平衡态, 坪台压力随温度的变化可推导出反应 (10) 的坪台热力学量:

H_α/ (b-a) →PdH_b/ (b-a) (10)

式中a和b分别为稀释相和氢化物相的组成。对两固相的p-c-T测量结果以及L sser等给出的坪台区数据列于表2。

表1 钯-氢体系的临界常数

Table 1Critical parameter of Palladium-Hydrogen system

体系	临界常数
体系	临界温度 T_c/K	临界压力 p_c/MPa	临界Q/Pa原子比 r_c (Q/Pd)
Pd-H	563	1.9	0.257
Pd-D	556	3.9	0.25
Pd-T	无临界常数, 但存在分歧

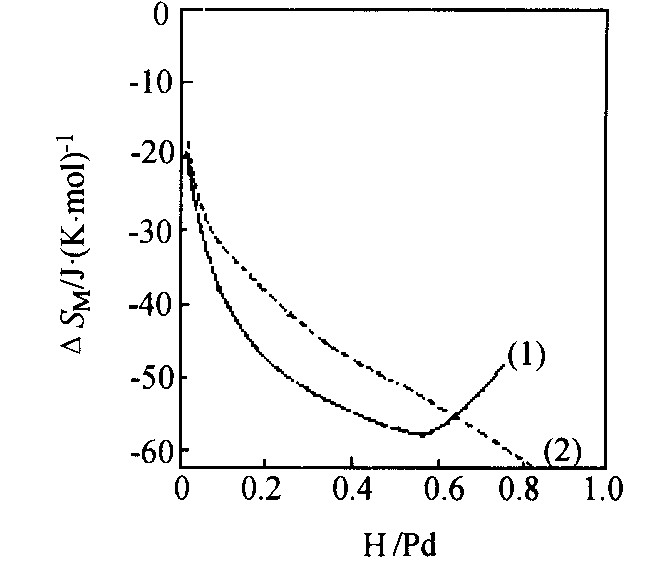
图4和5表明了ΔH_H和ΔS_H随r的变化, 可以看出ΔH_H和ΔS_H均存在最小值。此时希望的温度应高于T_c (热力学量才可能是r的连续函数) , 对于图4和5, 温度被人为地选择在500 K, 但仍假设氢化物相还未形成。

无限稀释时氢溶解的相对偏摩尔焓ΔH 具有特别重要的意义, 因为它不受H-H相互作用的影响, 所以其数值对于比较各种金属-氢体系是最有意义的。 ΔH 可由ΔH_H外推到r=0得到, 但也可由温度和p^1/2-r图的斜率之间的变化关系得到 (即Sieverts′定律作图法) 。后一种方法被L sser等 ^[27] 用于确定所有3种氢同位素从296～1500 K附近的ΔH 值。结合统计热力学方程, L sser等给出了温度与ΔH 的关系, 结果示于图6。无限稀的相对偏摩尔熵ΔS 也可用同样的方法确定。利用 [ 27] 的解析表达式, 得到298 K时ΔH =-9.92 kJ·mol^-1 H以及ΔH =-8.24 kJ·mol^-1 D。

表2 Pd-H和Pd-D两相坪台区的焓和熵

Table 2Enthalpy and entropy of plateau phase for Pd-H and Pd-D

H^f/ (kJ·mol^-1)	H^d/ (kJ·mol^-1)	S^f/ (kJ·mol^-1)	S^d/ (kJ·mol^-1)
范特霍夫焓
-18.70.15 (H)	19.50.25 (H)	-46.30.4 (H)	46.20.6 (H)
-16.80.30 (D)	17.70.25 (D)	-46.70.8 (D)	46.70.65 (D)
量热焓
-19.090.15 (H)	19.280.20 (H)	-46.6 (H)	46.6 (H)
-17.270.25 (D)	17.230.25 (D)	-46.6 (D)	46.4 (D)

图4 HH随r的变化

Fig.4 Variation of H_H with H/Pd=r

图5 ΔSH随r的变化

Fig.5 Variation of ΔS_H with H/Pd=r (1) 实验数据; (2) 理想状态

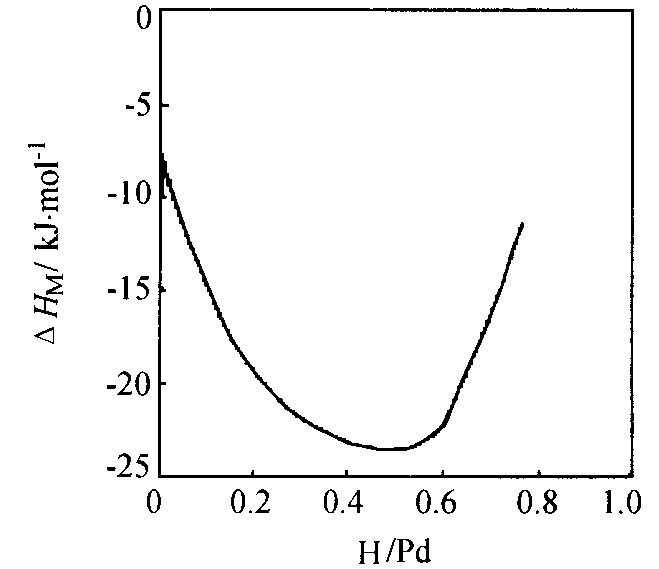
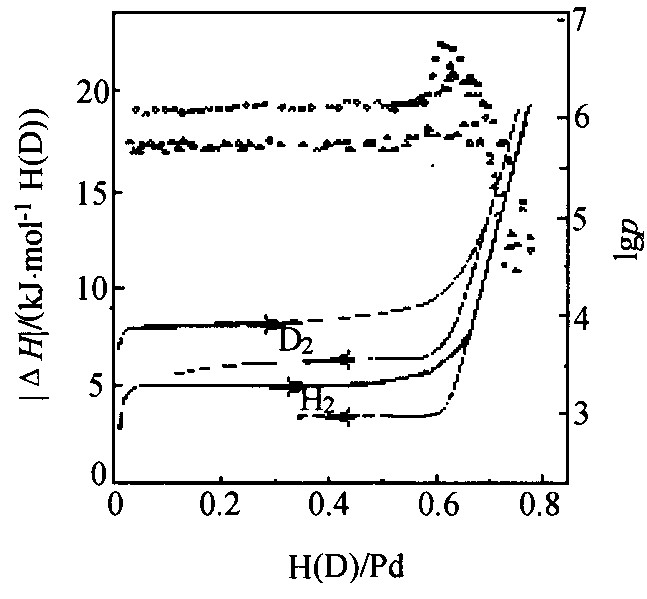
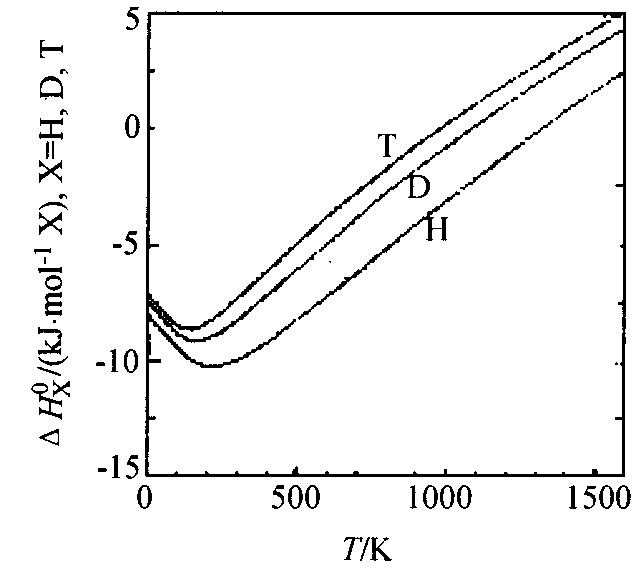
直接从反应量热确定焓变可替代p-c-T方法。图7显示了298 K时在两相平台区及单一β相区由反应热量决定的吸放氢 (氕、氘) 的相关焓变 ^[28] 。但列于表2由Van′t Hoff数据得到的吸放氢热焓在数值上的差别直接来源于滞后效应。由p-c-T数据得到的氢化物吸放氢热焓平均值与对Pd-H和Pd-D量热确定的数值几乎相等。

由量热计算的坪台区热焓几乎与温度无关。例如, Picard等 ^[29] 报道了598 K时的|ΔH_plat|=19.2 kJ·mol^-1, 这与298 K时的数值非常一致。两相区即坪台区的熵可用方程 (11) 从量热得到的焓变进行计算。

图6 ΔH0Η与温度的函数关系图

Fig.6 Plot of ΔH as a function of temperature

图7 量热法确定的298 K时Pd-H和Pd-D体系的焓变

Fig.7 Relative enthalpies for both Pd-H and Pd-D systems determined from reaction calorimetry (298 K) using Pd foil

式中的|ΔH_plat|是量热值, 。按此计算的数据与通过p-c-T测量得到的数据非常一致。

5 Pd氢化物的同位素效应

5.1 Pd氢化物中氢同位素效应的一般概念

L sser ^[30] 给出的一些同位素效应数据见图8。由图8可见, 在给定的氢压力下, 越轻的同位素的溶解度越大, 坪台压力也明显不同。钯-氢体系的同位素效应的根源是同位素气相分子和溶解原子的零点能不同 (见图9) 。

同位素分离因子 (例如H和D) 被定义为:

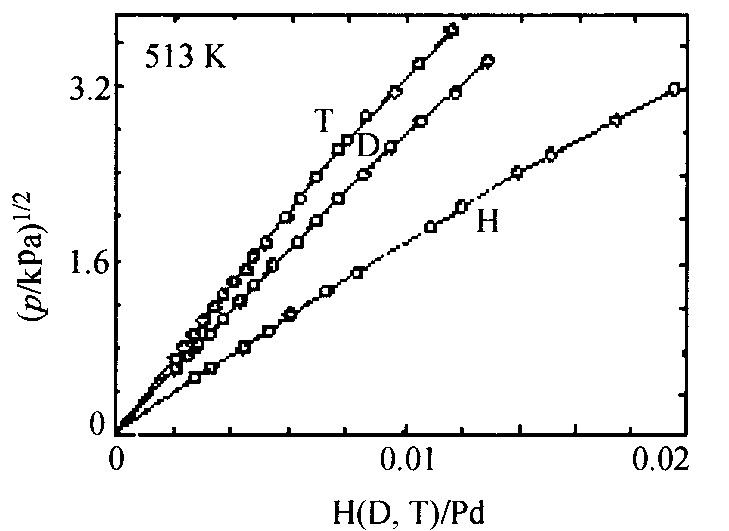
图8 α相氢溶解度的同位素效应

Fig.8 Isotopic effect of solubility in α-phase for palladium-hydrogen systems

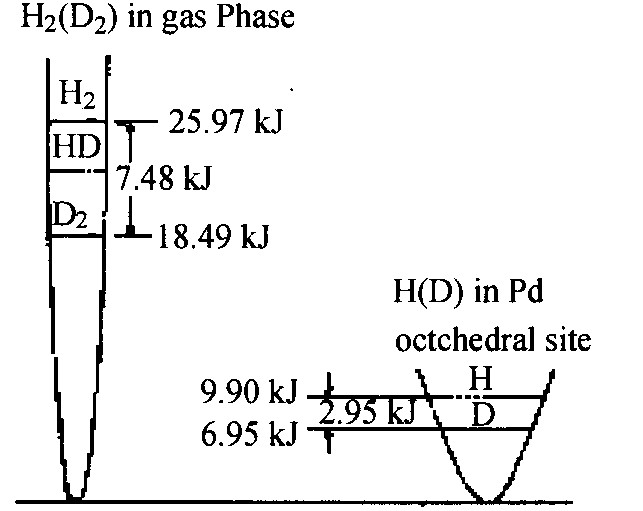
图9 气相与α相中H, D零点能级的相对位置

Fig.9 Relative location of the zero point energy levels of H and D in gas phase and dissolved in α-phase of palladium

式中x代表气相 (g) 或固相 (s) 中的给定氢同位素的摩尔分数。给出的同位素分离因子表达式未涉及氢-氢相互作用与同位素自身性质的关系。后来Brodousky等 ^[31] 考虑了这种关系的作用。有关扩散的同位素效应已在扩散一节中讨论。

5.2 Pd氢化物的氢同位素分离因子

Pd具有相当大的同位素效应 (分离因子) , 对此较少有文献报道。对Pd-H体系的分离因子结果相对完整的测量已由Fukada等 ^[32] 完成。他们给出了自己及其它作者的Pd中H, D在111 kPa总压时的分离因子, 也研究了总压高达1200 kPa的情况, 发现分离因子随总压力增加而轻微下降。

考虑平衡常数和分离因子的关系:

α=K/R (13)

对H-D交换反应K=0.5。平衡常数与反应的标准自由能G⁰的关系由下式给出,

ΔG⁰=-RTlnK (14)

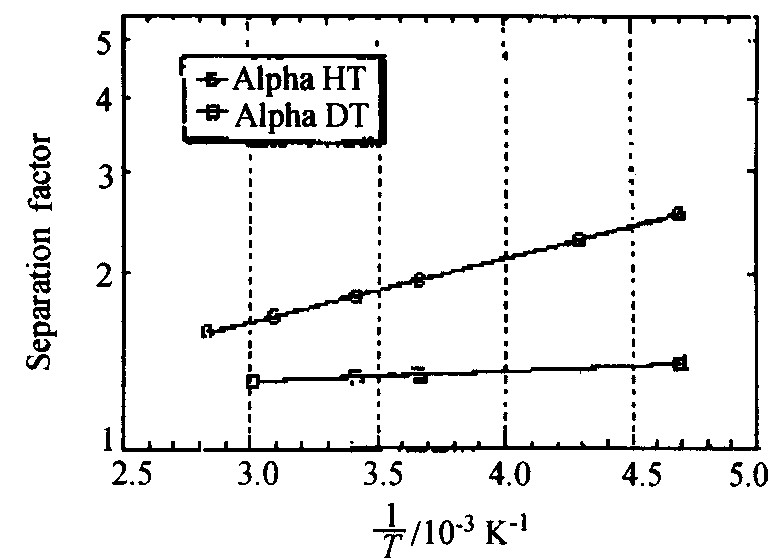
于是可得到lnα= (ΔH/T-ΔS) /R。这种模型对α相是有效的, 因为可从经典热力学推导出来。但是, 在Pd-H相图的β和两相区, 氢不是以纯组元形式存在, 而是分别以化合物及纯组元和化合物共存的形式存在, 所以理想溶液分析方法是不严格的, β相的分离因子与温度的关系将不同于前面的形式。不同作者给出了分离因子 (α) 与温度的关系列于表3。相比较而言, 在相同温度下, H-T混合物的分离因子更大, D-T的分离因子小于H-D。 H-T和D-T的分离因子示于图10 ^[37] 。

表3 分离因子 (α) 与温度 (T) 的关系

Table 3Variation relation of separation factor α with temperature

α-T的关系表达式	参考文献
α_H₂-HD=exp (228/T-0.121)	32
lgα=225/T-0.51	33
lgα=215/T-0.47	34
lnα=245/T+0.055	32
lgα=119/T-0.07 (固相D组成接近0%) lgα=82/T+0.025 (固相D组成为70%)	35
α=exp[-0.3+B (x_H) (·¹⁰⁰⁰_T) ^0.75] B (x_H) =0.50916-0.0037952x_H-0.15589x	36

图10 H-T和D-T的分离因子与温度关系

Fig.10 Relationship between separation factor of H-T and D-T and temperature

6 Pd-H反应动力学与表面

研究氢与单晶Pd的不同晶面的相互作用的方法有: 热脱附谱 (TDS) 、低能电子衍射 (LEED) 、离子散射及理论计算。观察到的反应行为与暴露给氢气的特定晶面有关。例如120 K时, (110) 晶面上首先形成有序氢 (2×1) 结构, 少于一个单层, 当覆盖度增加时, (1×2) 的重构表面开始出现 ^[38,39] 。缓慢加热至180 K, (1×2) 结构慢慢消失, 而 (2×1) 结构开始生长。 Felter 等 ^[40] 从H在 (111) 晶面上的LEED研究中发现, H致重构并不发生。对于清洁的钯表面, 氢的吸附速率很快。 Kay等 ^[41] 报道了在适当高压 (500 Pa) , 温度333～413 K时, Pd在α相吸氢速率是体扩散控制, 而不是以前研究发现的在不太清洁的Pd表面 ^[42] 上所提出的表面解离是慢反应步骤。

7 钯-氚体系的氚老化效应

用于氚工艺的金属氢化物会在晶格中积累氚衰变产物³He。由³He引起的金属氢化物晶体结构变化导致金属氢化物的吸放氢性能变化。 Nobile等 ^[43] 研究了Pd的氚老化效应, 发现Pd的吸放氢热力学只发生轻微变化, 并给出了坪台 (α+β相) 的变化。 Walters等 ^[44] 报道了在坪台的低浓度区, 解吸压力变小。

Pd放氢等温线所观察到的压力变化是温度的函数, 这是由于³He聚积导致晶格结构变化引起的。以前对³He释放的测量 ^[45,46] 已表明大部分³He保留在晶格中。 Thomas等 ^[47] 的实验表明从³He产生的一刻起就立即对晶格造成损害, 这与Nobile ^[43] 所发现的结果一致, 并且发现初始的解吸压力发生很大变化似乎是初始晶格中位错引起的应力所致。正如Lasser等 ^[48] 描述的一样, 存在应力的晶格含有空位、位错和自间隙缺陷。 Thomas等 ^[47] 在氚老化65d的样品中发现直径1.5～2.0 nm的³He泡, 这可以认为位错的形成和应力为³He泡的形成提供了途径。这种图象与空位形成以及最终形成³He泡是以Wilson等 ^[49] 所描述的自捕获机理为基础的。 ³He泡中的³He几乎不可能有效地造成局部位错和晶格损伤, 这也解释了样品在较长的老化时间 (10～133 d) 后等温线压力只有很小的下降。大于400 d发生等温线更大变化的机理还不清楚, 但表现出更混乱的状态: ³He泡合并、贯穿等。

8 结束语

综上所述, 各国学者对钯-氢体系的研究是较为深入的, 但是一些基础问题的分歧依然存在, 数据的差异也比较明显, 钯的粒度及纯度对钯-氢体系的热动力学、氢的扩散特性、氢同位素分离性能以及溶解度等物化性能都存在影响, 氢同位素在不同形态钯表面的交换机理仍有待进一步研究, 钯的氚老化效应的微观机制仍不完全清楚, 因此, 对钯-氢体系的系统研究还需继续深入。