一种基于相对位移的铰缝传力性能评估方法

刘晓春，卫军，李沛，余志武

(中南大学 土木工程学院，湖南 长沙，410075)

摘 要：

酷环境因素的长期作用下，装配式混凝土板梁桥的铰缝损伤诱发的铰缝开裂、渗水及桥面铺装错台等病害现象非常普遍。基于板梁桥铰缝的受力状态和变形形态的分析，提出采用铰缝处板梁间的相对位移与板梁挠度的比值来描述铰缝的损伤度的构想，建立考虑铰缝损伤的板梁桥的铰缝传力模型。结合板梁桥静载试验中多点加载及荷载偏心情况，提出以铰缝的损伤度为评价指标的板梁桥铰缝损伤及其横向传力性能的定量评估方法。实桥静载试验资料的验证结果证明，提出的铰缝损伤度评价指标及传力性能评估方法是合理的，可用于实际工程中混凝土板梁桥的受力状态评估。

关键词：

板梁桥；铰缝；损伤；相对位移；传力性能；评估；

中图分类号：U446.1; TU317.2          文献标志码：A         文章编号：1672-7207(2013)08-3377-07

Load-transmitting performance evaluation method for hinge joint based on relative displacement

LIU Xiaochun, WEI Jun, LI Pei, YU Zhiwu

(School of Civil Engineering, Central South University, Changsha 410075, China)

Abstract: Damaged hinge joint induced diseases such as cracking, seepage and pavement faulting usually appear in fabricated concrete plate-girder bridge under the long-term action of the overload transportation and harsh environmental factors. Based on the stress state and deformation analysis of plate girders and hinge joint, a conception of using the ratio of relative displacement adjacent to hinge joint and the general deflection of plate girder beam is put forward to describe the damage degree of hinge joint. Hinge joint load transfer model considering the damage of hinge joint is established for fabricated plate-girder bridge. Combined with multi-point and eccentric loading situation in conventional static loading test of highway bridges, a quantitative assessment method is put forward to evaluate the damage degree and lateral load transmission performance of hinge joint in fabricated plate-girder bridge. Several real bridge static load test data is used to validate the feasibility of the proposed model, and the results prove that the hinge joint damage evaluation index and load transmission performance evaluation method are reasonable and they can be used in technical condition evaluation of fabricated plate girder bridge in the practical engineering.

Key words: plate-girder bridge; hinge joint; damage; relative displacement; load transmission performance; evaluation

由于中小跨径装配式混凝土空心板梁桥存在设计阶段考虑不周、施工阶段质量控制不严、运营阶段超载监管不力及环境因素的长期作用等问题，现役装配式混凝土空心板梁桥铰缝处出现纵向开裂、渗水乃至桥面铺装错台等不同程度的病害现象非常普遍^[1-2]。铰缝是装配式板梁桥中的主要横向传力部件，一旦铰缝出现损伤，将直接影响空心板梁桥的横向整体工作性能，甚至造成极为不利的“单板受力”，大大缩短桥用寿命。因此，开展铰缝的损伤程度和传力性能评估，对保障装配式混凝土空心板梁桥的服役安全具有重要的实用意义。实际工程中一般通过定期开展的人工外观检查判断铰缝的损伤程度，必要时通过静力荷载试验结果评估铰缝的横向传力性能^[3]。长安大学、内蒙古工业大学等单位先后开展了装配式混凝土空心板梁桥铰缝受力性能及损伤破坏机理的试验研究^[4-6]，得出铰缝传力性能的主要影响因素及铰缝损伤破坏规律，但目前还处于定性研究阶段，尚无合适的定量评价指标及评估模型；有些学者先后提出了采用瞬态动力分析和信赖域算法识别铰缝损伤及横向连接刚度^[7-8]，但动力测试的影响因素更多，参数识别方法也更为复杂。本文作者拟通过对装配式混凝土空心板梁桥铰缝的受力状态及变形形态的分析，提出一种基于铰缝相对位移的铰缝损伤模型，对荷载试验的板梁挠度进行分析，给出确定铰缝横向传力性能退化程度的评价指标和方法，从而实现定量评价铰缝的损伤程度和横向传力性能的目的。

1  铰缝损伤程度的描述

为了定量地评估铰缝的传力性能，首先需要实现铰缝损伤的定量描述。尽管现役的装配式混凝土空心板梁桥在使用过程中铰缝出现纵向开裂、渗水乃至桥面铺装错台等不同程度损伤的现象非常普遍，国内外有许多学者开展了铰缝损伤的理论和试验研究，但目前尚无一个学术界公认的铰缝损伤定量描述方法。

依托西部交通项目，本文开展了钢筋锈蚀诱发铰缝损伤的试验研究^[9]，发现当铰缝完好无损时，铰缝处板梁间的相对位移可以忽略不计，空心板梁协同工作性能良好；当铰缝损伤严重乃至破坏后，铰缝处板梁间出现明显的相对位移，空心板梁的协同工作性能严重退化，甚至呈现出典型的“单板受力”特征。因此，提出了利用铰缝处相对位移与板梁挠度之间的关系评价铰缝损伤程度及空心板梁协同工作性能的构想。这里，定义铰缝的损伤程度(以下简称“铰缝的损伤度”)变量D_i如下：

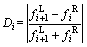               (1)

式中：D_i为第i条铰缝的损伤度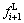；和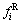分别次为第i条铰缝右侧板梁的左下端挠度及左侧板梁的右下端挠度，以竖直向下为正。

由式(1)可知：铰缝的损伤度D_i为一个无量纲的标量：当铰缝完好无损时，铰缝处板梁间的相对位移为0，即D_i=0；当铰缝完全失效出现“单板受力”时，D_i=1；当铰缝出现一定程度的损伤时，D_i在0~1之间变化。

式(1)中分子为铰缝处左右两侧板梁间的相对位移，分母为铰缝处左右两侧板梁的挠度之和。分子与板梁刚度、荷载分布特征及铰缝剪力等因素有关；分母则只与板梁的抗弯、抗扭刚度及荷载分布特征等因素有关，而与该条铰缝传递的剪力无关，可见式(1)定义的D_i是一个表征铰缝传力效率的物理量，将其作为铰缝损伤程度及其传力性能的评价指标是可行的。

2  考虑铰缝损伤的混凝土板梁桥受力分析模型

采用铰缝连接的混凝土空心板简支梁桥，其受力类似于数根并列而相互间横向铰接的狭长板梁，如图1所示。对于这一类板梁，通常采用横向铰接板模型分析荷载的横向分配^[10]。简支板梁桥设计时通常假定铰缝传力性能良好，铰缝处板梁间不会发生相对位移；而实际工程中在役的空心板梁桥由于超载及环境因素共同作用所带来的铰缝损伤等不利影响，车辆荷载作用下铰缝处板梁间往往会出现相对位移^[11]。为了考虑铰缝损伤的影响，需要在装配式混凝土空心板梁桥的受力分析模型中引入铰缝处板梁间相对位移的影响。

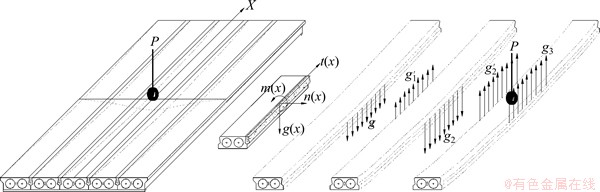
图1  装配式混凝土板梁桥受力示意图

Fig. 1  Mechanical schematic diagram for a hinge joint fabricated concrete plate-girder bridge

2.1  基本假定

本文基于横向铰接模型的基本假设^[10]，考虑铰缝损伤对装配式混凝土空心板梁桥传力性能的影响，提出以下基本假定：

(1) 板梁沿纵向是可变形的，在横向是刚性的。

(2) 板梁上荷载、铰缝剪力、板梁的位移等沿跨径方向为半波正弦分布。

(3) 只考虑铰缝传递竖向剪力，不考虑可能传递的纵向剪力、横向弯矩及法向正应力。

(4) 不考虑材料泊松比υ的影响。

(5) 铰缝处板梁之间相对位移与铰缝传递的剪力成正比，与铰缝的抗剪刚度成反比。

由此可得装配式混凝土空心板梁桥的横向受力计算图式如图2所示，铰缝的剪切变形如图3所示。其中，n块板梁自左向右编号依次从1到n，(n-1)条铰缝自左向右编号依次从1到(n-1)。荷载、内力及位移的方向统一规定如下：板梁上竖向荷载及竖向位移以向下为正，竖向荷载的横向偏心及铰缝的剪力以使板梁发生顺时针转动为正，铰缝处板梁间相对位移以左下右上为正。

根据材料力学中剪切作用所引起的挠度w_t的计算式为^[1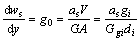2]：

          (2)

对于横向传力的铰缝，可认为剪力大在铰缝横向范围内保持不变，因此，在计算宽度c_i范围内铰缝剪切作用引起的挠度为：

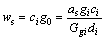             (3)

式中：a_s为截面的剪切系数，对矩形截面，a_s=3/2。

2.2  考虑相对位移的铰缝剪力正则方程

横向铰接板模型假定铰缝的抗剪刚度G_gi 足够大，依据相邻两块板梁边的相对位移为0建立铰缝剪力的正则方程。考虑在役的装配式混凝土空心板梁桥铰缝损伤的不利影响，第i条铰缝的实际抗剪刚度将发生退化，假定损伤后铰缝的抗剪刚度为(1-D_i)G_gi(其中G_gi为未发生损伤的铰缝抗剪刚度) ，由图3可得铰缝处板梁间的相对位移为：

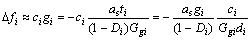  (4)

根据铰缝处板梁间的变形协调条件，可得横向铰接板的力法正则方程：

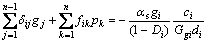
(i=1，2，…，n-1)            (5)

式中：△_ij和f_ik分别为第j条铰缝处单位铰缝剪力及第k块板梁上单位竖向荷载在第i条铰缝处产生的相对位移；g_i和g_j分别为第i条和第j条铰缝处的铰缝剪力；p_k为第k块板梁上的竖向荷载，其相对第k块板梁中心的偏心为e_k。

2.3  铰缝剪力及板梁上竖向荷载产生铰缝相对位移的计算

由图1所示板梁的变形特点，可计算式(5)第i条铰缝处产生的相对位移△_ij和f_ik。第j条铰缝单位剪力g_j=1单独作用时，只会引起该铰缝及左右紧邻的两条铰缝处板梁的相对位移，则第i条铰缝处的相对位移 △_ij为：

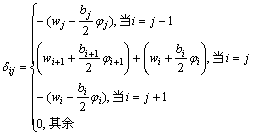   (6)

式中：w_i为单位中心荷载在第i块板梁上产生的跨中挠度，可参考文献[10]计算；b_i为板梁宽度；φ_i为单位扭矩在第i块板上产生跨中扭转的转角，可参考文献[10]计算。

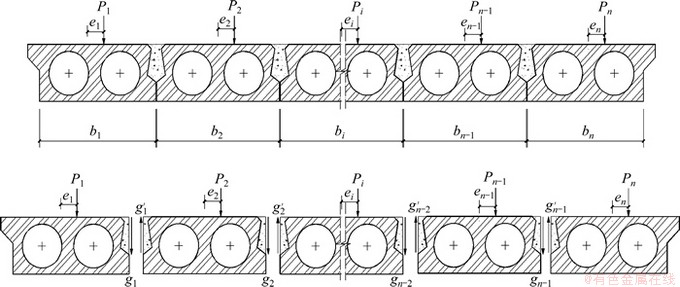
图2  装配式混凝土板梁桥横向受力计算图式

Fig. 2  Mechanical model of transverse force for a hinge joint fabricated concrete plate-girder bridge

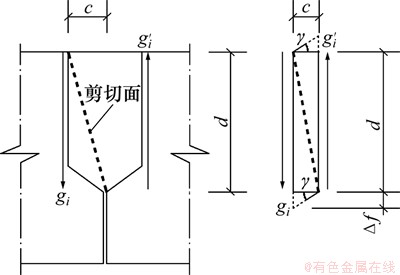
图3  铰缝的剪切变形示意图

Fig. 3  Schematic diagram for the shear deformation of a hinge joint

在第k块板梁上单位荷载p_k=1单独作用下，只会引起第k块板梁上左右两侧铰缝的相对位移，则第i条铰缝处的相对位移f_ik为：

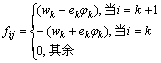          (7)

在铰缝剪力及竖向偏心荷载作用下每块板梁的竖向挠度均可根据平动变位与转动变位叠加的方法计算，如图4所示。

2.4  铰缝剪力的计算

根据横向铰接板模型^[7](参考文献的指向前后不一致，前有2处为^[10]，这里又指向^[7])，一组纵向正弦分布荷载作用在桥面上时，同一横截面上各块板梁中心的竖向位移f_i与该板梁所分担的荷载Q_i成正比，与该板梁的抗弯刚度EI_i成反比，即

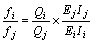              (8)

依据竖向力的平衡条件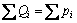，可得：

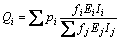           (9)

实际工程中除左右两端板梁截面形状略有不同外，中部板梁一般都采用相同的截面，可近似按所有板梁都相同的情况来考虑，则上式可简化为：

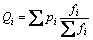            (10)

根据每块板梁在竖直方向力的平衡条件，有：

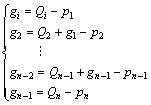        (11)

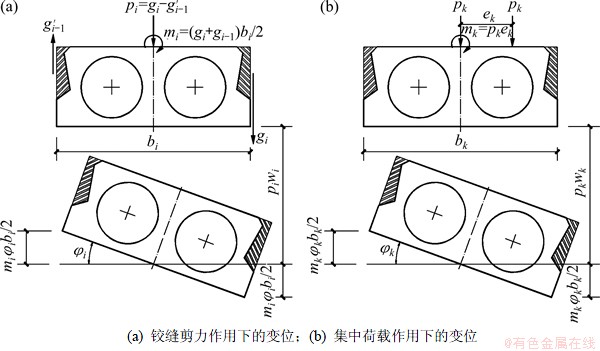
图4  单块板梁的变位特征

Fig. 4  Characteristics of displacement for a plate-girder

根据静载试验中得到在一组荷载p_i(i=1，n)作用下实测的各板梁中心所发生的竖向位移f_i( i=1，n)，代入式(10)可以得到各板梁所分担的荷载Q_i，将其代入式(11)即可得到各铰缝的剪力g_k。

2.5  铰缝损伤度D_i的求解

将板梁上荷载系列p_i( i=1，n)，式(6)，式(7)及式(11)得到的铰缝剪力代入式(5)，即可建立铰缝损伤度D_i与板梁位移之间的关系。当所有板梁及铰缝都相同时，式(5)可写成：

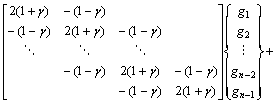
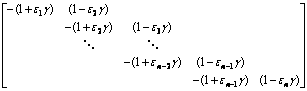
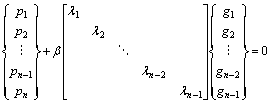 (12)

其中：，，。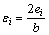

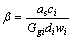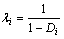λ_i为无量纲参数，定义为铰缝柔度增大系数。λ_i越大，铰缝刚度越小，柔度越大。根据式(12)可得到(n-1)个方程，可求解(n-1)个未知量λ_i(i=1，2，…，n-1)，进而可得出铰缝的损伤度D_i(i=1，2，…，n-1)。

3  铰缝横向传力性能的评估方法

3.1  铰缝损伤评估的最小二乘法

尽管实际工程中可通过人工外观检查定性地判断装配式混凝土空心板梁桥铰缝的损伤程度，但定量的评价往往仍然需要依赖于桥梁的静力荷载试验^[3]。静载试验中通常采用标准试验车辆加载，由于受到车辆轮距及轴距等限制，往往不可避免地存在多个集中荷载同时作用以及荷载不同程度偏心的问题，因此，各块板梁挠度、各条铰缝的剪力之间存在相互耦合关系。此外，为了综合评价各块板梁的受力性能及铰缝的传力性能，实际工程中通常需要考虑横向中载、偏载及各种纵向不利布置等多种工况进行荷载试验。由于荷载的横向偏心、纵向加载位置及加载效率各不相同，简单根据其中某一组试验结果得出的板梁铰缝损伤度评估铰缝的传力性能是不全面的，更为科学的做法是基于多组试验结果综合评估的铰缝损伤及传力性能。

假定由n块板梁和(n-1)条铰缝连接的简支空心板梁桥，静载试验中考虑了m种不同的加载工况，每一种工况静载试验中均可测得所有板梁的中心挠度f_i，并可推导出一组铰缝的剪力g_i及相应的板梁铰缝损伤度D_i。根据式(1)对每一种工况均可列出(n-1)个方程，m种不同的工况则共有m×(n-1)个方程，需要求解的未知量只有(n-1)个，方程组没有精确解。对于数学中的这一类超定方程组，通常采用最小二乘法，满足残差的2-范数最小时的参数值即为超定方程组的最小二乘解。

对于式(5)，m组试验总残差的2-范数为：

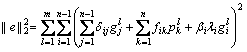  (13)

假定铰缝正则方程中各变量相互独立，因此，可令第i个未知量λ_i残差的2-范数最小，得出铰缝柔度增大系数的最小二乘解为：

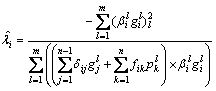    (14)

由式(14)可知：采用最小二乘法评估铰缝损伤时，铰缝剪力越大，铰缝处板梁间相对位移越大，则这种工况在评价铰缝损伤时的权重越大，反之亦然，因此，为了提高铰缝损伤评估的精度，荷载试验时应尽可能采用使该铰缝产生较大相对位移的荷载布置方案，即荷载只在铰缝单侧布置且车轮离铰缝越近越好。

3.2  铰缝损伤及传力性能的评定

根据现行的JTG/T H21—2011《公路桥梁技术状况评定标准》^[3]，当混凝土桥面接缝两侧高差(错台)达到△f=10 mm时，即认为出现了严重缺损和功能降低，进一步恶化将不利于主要部件的正常工作，影响正常交通；对于混凝土梁式桥，将跨中挠度f≥l/1 000作为判定桥梁上部结构达到中等缺损，但尚能维持正常使用状态的标准；将f≥l/600作为判定桥梁主要构件存在严重缺损，危及桥梁安全的标准。参考上述规定，可初步拟定铰缝的损伤程度和传力性能的判定标准如下：

当损伤度D_i＜300△f /l时，可认为铰缝传力性能良好，可不作处理；

当损伤度300△f/l≤D_i＜500△f/l时，可认为铰缝达到中等损伤，传力性能退化，需予以修复；

当损伤度D_i≥500△f /l时，可认为铰缝严重损伤，传力性能严重退化，需拆除重做。

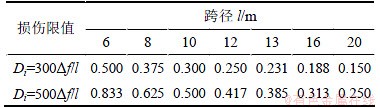
对于常用跨径为6.0~20.0 m的装配式混凝土空心板梁桥，评判铰缝损伤程度的损伤限值如表1所示。

表1  装配式混凝土空心板梁桥铰缝损伤限值

Table 1  Limit values for damage evaluation for hinge joints in fabricated concrete plate-girder bridge

4  工程实例

为了验证本文提出的铰缝损伤变量及铰缝传力性能的评估方法的可行性，选取了宣大高速河北段某单孔跨径6 m的装配式混凝土空心板梁桥的静载试验资料^[11]进行分析。采用本文提出的铰缝传力模型，得出装配式混凝土空心板梁桥铰缝传递的剪力及铰缝处的相对位移如图5所示，各条铰缝的损伤度如图6所示。

由图5和6可知：铰缝传递的剪力及铰缝处板梁相对位移的分布规律大体是一致的，二者分布规律有明显不一致的位置，往往是铰缝损伤程度差别较大的位置。将图6基于相对位移得出的铰缝损伤度与表1所列的损伤限值比较，第4~8条及第12条铰缝的损伤度D_i≥500△f/l时，铰缝严重损伤，传力性能严重退化，需拆除重做；第1条、第2条、第10条及第11条铰缝损伤度300△f/l≤D_i＜500△f/l时，铰缝达到中等损伤，传力性能退化，需予以修复。

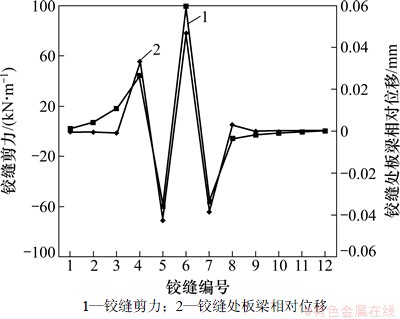
图5  铰缝传递的剪力及铰缝处的相对位移

Fig. 5  Shear transferred by damaged hinge joints and relative displacements

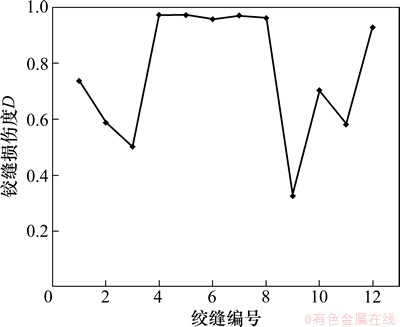
图6  基于相对位移的铰缝损伤度

Fig. 6  Damage degree of hinge joints derived by relative displacements

需要指出的是，上述分析依据单一的加载工况推导的铰缝损伤度，得出加载点邻近的铰缝损伤度的精度相对较高，而远离加载点的铰缝精度则相对偏低。因此，实际工程中对于存在表观破损的铰缝，应在铰缝临近两侧布置加载点，依据多种工况的测试结果采用3.1节的方法综合评价铰缝的损伤程度和传力性能。

5  结论

(1) 利用铰缝处相对位移与板梁挠度的比值来定义铰缝的损伤度D_i，具有明确的物理意义，将其作为铰缝损伤程度及其传力性能的评价指标是可行的。

(2) 考虑铰缝处的横向剪切变形的影响，在装配式混凝土空心板梁桥的横向铰接板分析模型中引入铰缝损伤及板梁间相对位移，本文提出了一种可以考虑铰缝损伤的装配式混凝土空心板梁桥受力分析模型。该模型能够考虑铰缝的相对位移、静载试验中多个荷载及荷载偏心的影响，实桥试验数据的结果证明，本模型给出的铰缝剪力和铰缝相对位移等结果是可靠的。

(3) 结合公路桥梁技术状况评定标准，提出了装配式混凝土空心板梁桥铰缝损伤的评定方法及损伤限值，将300△f/l及500△f/l分别作为铰缝达到中等损伤需要予以修复及铰缝达到严重损伤需拆除重做的损伤限值是基本合适的。

参考文献：

[1] 史建方. 桥梁单板受力成因分析和防治对策[J]. 公路, 2004(10): 71-73.

SHI Jianfang. Origin analysis of the single slab bearing of bridges and countermeasures[J]. Highway, 2004(10): 71-73.

[2] 黄民水, 朱宏平. 空心板梁桥“单板受力”病害机理及其加固处治研究[J]. 华中科技大学学报: 自然科学版, 2008, 36(2): 118-121.

HUANG Minshui, ZHU Hongping. Study on mechanism processing and reinforcement of “single slab bearing” disease of hollow core slab beam bridge[J]. Journal of Huazhong University of Science and Technology: Nature Science Edition, 2008, 36(2): 118-121.

[3] JTG/T H21—2011, 公路桥梁技术状况评定标准[S].

JTG/T H21—2011, Standards for technical condition evaluation of highway bridges[S].

[4] 乔学礼. 空心板铰缝破坏机理及防治措施研究[D]. 西安: 长安大学公路学院, 2008: 1-62.

QIAO Xueli. Study on damage mechanism and prevention measures of hollow slab joints[D]. Xi’an: Chang’an University. School of highway, 2008: 1-62.

[5] 董海航. 装配式板桥铰缝受力机理与耐用性能研究[D]. 西安: 长安大学公路学院, 2010: 1-71.

DONG Haihang. Study on force mechanism and durability of fabricated slab bridge hinge joint[D]. Xi’an: Chang’an University. School of Highway, 2010: 1-71.

[6] 杨继新. 装配式空心板桥铰缝受力性能研究[D]. 呼和浩特: 内蒙古工业大学土木工程学院, 2009: 1-100.

YANG Jixin. Study on Mechanical Properties of fabricated hollow slab bridge hinge joints under the load[D]. Hohhot: Inner Mongolia University of Technology. College of Civil Engineering, 2009: 1-100.

[7] 邹毅松, 袁波波, 王银辉, 等. 基于瞬态动力分析的装配式板桥铰缝损伤识别[J]. 重庆交通大学学报: 自然科学版, 2011, 30(1): 1-3, 43.

ZOU Yisong, YUANG Bobo, WANG Yinhui, et al. Damage identification of hinged joints of prefabricated slab bridges based on transient dynamics analysis[J]. Journal of Chongqing Jiaotong University: Natural Science, 2011, 30(1): 1-3, 43.

[8] 窦勇芝, 王复明, 蔡迎春. 基于信赖域算法的板梁桥横向连接刚度的参数识别[J]. 结构工程师, 2006, 22(6): 25-29.

DOU Yongzhi, WANG Fumin, CAI Yingchun. Parameter identification of transverse coupling stiffness for plate girder bridges based on trust region algorithm[J]. Structural Engineers, 2006, 22(6): 25-29.

[9] 卫军, 李沛, 张国法, 等. 空心板铰缝结构耐用性能的试验研究[J]. 华中科技大学学报: 自然科学版, 2012, 40(1): 77-81.

WEI Jun, LI Pei, ZHANG Guofa, et al. Experimental study on durability performance of hollow slab hinged joint[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2012, 40(1): 77-81.

[10] 李国豪, 石洞. 公路桥梁荷载横向分布计算[M]. 2版. 北京: 人民交通出版社, 1987: 87-95.

LI Guohao, SHI Dong. Calculation of load transverse distribution of highway bridges[M]. 2nd ed. Beijing: People's Transportation Press, 1987: 87-95.

[11] 秦禄生. 重载条件下小跨径简支板桥的横向铰接能力分析[J]. 公路, 2007(10): 14-16.

QIN Lusheng. Transverse hinged capacity analysis of small span simple supported slab bridge under overload condition[J]. Highway, 2007(10): 14-16.

[12] Timoshenko S. 材料力学[M]. 北京: 科学出版社, 1990: 210-217.

Timoshenko S. Mechanics of materials[M]. Beijing: Science Press, 1990: 210-217.

(编辑  陈爱华)

收稿日期：2012-09-04；修回日期：2012-12-04

基金项目：国家自然科学基金资助项目(51008312)；煤炭联合基金资助项目(51174291)；中国博士后科学基金资助项目(2012M5117587)

通信作者：刘晓春(1980-)，男，湖北蕲春人，博士后，讲师，从事结构安全性及混凝土结构耐久性等领域的研究；电话：0731-82539752；E-mail：xchliu@csu.edu.cn

摘要：在超载运输及严酷环境因素的长期作用下，装配式混凝土板梁桥的铰缝损伤诱发的铰缝开裂、渗水及桥面铺装错台等病害现象非常普遍。基于板梁桥铰缝的受力状态和变形形态的分析，提出采用铰缝处板梁间的相对位移与板梁挠度的比值来描述铰缝的损伤度的构想，建立考虑铰缝损伤的板梁桥的铰缝传力模型。结合板梁桥静载试验中多点加载及荷载偏心情况，提出以铰缝的损伤度为评价指标的板梁桥铰缝损伤及其横向传力性能的定量评估方法。实桥静载试验资料的验证结果证明，提出的铰缝损伤度评价指标及传力性能评估方法是合理的，可用于实际工程中混凝土板梁桥的受力状态评估。