温度变化对动应变相关函数幅值向量的影响
李苗1, 2,任伟新1,王宁波1
(1. 中南大学 土木工程学院,湖南 长沙,410075;
2. 湖南城市学院 土木工程学院,湖南 益阳,413000)
摘 要:
测动应变相关函数幅值向量的变化情况。采用基于主成分分析的环境温度影响剔除方法,寻找主要反映应变时程温度信息的特征子空间。对时程数据重构,得到温度效应成分,由此消除温度对应变信号的影响。研究结果表明:第一主成分反映了动应变时程绝大部分的波动信息;通过第一主成分特征向量可有效提取应变时程中的温度效应成分。基于实测动应变的相关函数幅值向量在各时段的比例形态均存在较大差异,剔除温度效应成分后的相关函数幅值向量呈现一致的比例线形,说明应变时程中的温度效应成分会导致相关函数幅值向量的比例线形发生改变;不考虑环境温度对动应变时程相关函数幅值向量的影响,易对桥梁结构的健康状况产生误判。
关键词:
中图分类号:U441 文献标志码:A 文章编号:1672-7207(2013)09-3834-09
Effect of varying temperature on correlation function amplitude vector of dynamic strain
LI Miao1,2, REN Weixin1, WANG Ningbo1
(1. School of Civil Engineering and Architecture, Central South University, Changsha 410075, China;
2. School of Civil Engineering, Hunan City University, Yiyang 413000, China)
Abstract: Under varying temperature, correlation function amplitude vector of the measured dynamic strain was analyzed. Based on principal component analysis, the method for eliminating the effect of environmental temperature was applied to study the eigenspace reflecting temperature variation. By reconstruction of data, the temperature effect on strain history was eliminated. The results show that the first principal component reflects most of the volatility of data information. With eigenvector of the first principal component, the temperature effect components of strain history are effectively extracted. In different periods, the shape of correlation function amplitude vector (corV) based on measured data is distinct. When temperature effect component is eliminated, the shape of corV performs consistently. The temperature effect component in test data leads to various shapes of corV. Therefore, ignoring the effect of temperature on the corV of strain history is prone to get the false judgment on the real operation condition of structure.
Key words: dynamic strain; correlation function amplitude vector; temperature effect; principal component analysis
在结构健康监测系统中,传感器所测数据包含了大量的结构特征信息,结构损伤势必引起结构动力特性的改变,因此,动力特性的变化信息将包含在动力测试数据中。这类通过结构响应在时域建立损伤特征的思路更符合结构健康监测的概念。文献[1-3]利用结构在随机激励下某点响应(如加速度)与其相邻点响应之间的相关函数构造了相关函数幅值向量corV。corV仅与结构的频响函数有关,规范化后的corV应具有固定的比例形式;构造损伤因子即相关函数幅值向量置信度CcorV来标定结构corV的变化,根据损伤结构与无损结构间的置信度随损伤程度增大而下降的特性,可判断结构的损伤。结构在运营过程中会受到环境因素和运营条件(如温度、温度梯度、湿度、风和交通等)的影响。有研究表明,从结构响应信号中提取出的一些损伤特征(如模态频率等)会随环境因素和运营条件的改变而发生变化[4-12],而且这种变化有时会淹没或掩盖结构因损伤造成损伤特征发生改变[13]。时域特征corV是否也会出现类似的现象,本文分别采用桥梁结构实测原始应变时程和去除温度效应后的应变时程构造corV,对比分析温度变化对基于应变响应corV的影响。剔除应变时程中温度效应成分的思路是通过对原始应变时程进行主成分分析,找出主要反映温度信息的特征子空间,再对实测应变数据进行重构,提取温度效应成分,由此达到消除温度变化对应变信号影响的目的。
1 基于相关函数幅值向量的结构损伤识别
结构在随机振动下(交通荷载、地震、风等)同时得到其n个测点的响应信号。对于采样时间为T,采样间隔为 ,样本数为
,样本数为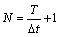 的时间序列,测点p的响应
的时间序列,测点p的响应 与测点l的响应
与测点l的响应 (l=1, 2, 3, …, n)之间的互相关函数
(l=1, 2, 3, …, n)之间的互相关函数 可表示成
可表示成
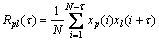 ;k=0, 1, 2, …, N (1)
;k=0, 1, 2, …, N (1)
当p=l时,所求 为自相关函数。
为自相关函数。
定义两测点p和l之间的相关函数幅值为 ,将所有的
,将所有的 组成向量,称其为以p为参考点的相关函数幅值向量,记为corV:
组成向量,称其为以p为参考点的相关函数幅值向量,记为corV:
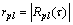 (2)
(2)
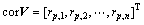 (3)
(3)
在随机激励下,结构响应的相关函数仅与结构的频响有关,因此,相关函数幅值向量中各元素的比例会比较固定,即幅值向量具有固定的曲线形态,仅会因外激励幅值的变化,导致各corV曲线上下平移。若对corV进行规范化处理,则各corV曲线几乎吻合[1]。当结构参数发生改变时,会导致corV中各元素的比例发生变化。以结构在健康状态下的corVr作为基准,将运营期的corV与之进行对比,这corV样,可通过运营期corV的变化情况来判断结构是否出现异常。
判断两组向量的一致性,可采用相关函数幅值向量置信度CcorV [1]:
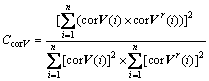 (4)
(4)
CcorV的取值范围为[0, 1],其值越小,表示2个相关函数幅值向量的一致性越低,说明结构出现了异常或者损伤。
2 基于主成分分析的环境因素影响的消除
假设Y为一反映结构动力特征的样本,
 (5)
(5)
式中: 为运营条件和环境因素变量的函数(T, L和W分别代表温度、交通和风);
为运营条件和环境因素变量的函数(T, L和W分别代表温度、交通和风);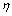 为与结构损伤和噪音相关的变量。
为与结构损伤和噪音相关的变量。
函数 大致由2部分映射过程构成[14]:非线性映射M和线性映射
大致由2部分映射过程构成[14]:非线性映射M和线性映射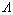 ,见图1。通过非线性映射M,运营条件和环境因素
,见图1。通过非线性映射M,运营条件和环境因素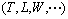 转换成不可观测因素
转换成不可观测因素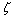 :
:
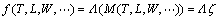 (6)
(6)
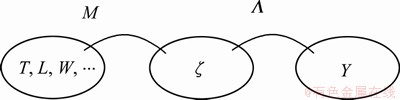
图1 函数f的映射过程
Fig.1 Mapping process of function f
不可观测因素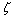 可视为零均值的不相关变量。对不可观测因素
可视为零均值的不相关变量。对不可观测因素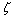 和结构动力特征建立线性映射
和结构动力特征建立线性映射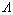 ,式(5)可表示为
,式(5)可表示为
 (7)
(7)
为确定不可观测因素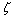 和结构动力特征之间的线性映射
和结构动力特征之间的线性映射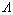 ,需长时间对健康状态下的结构进行测试,以充分反映环境因素对结构动力特征的影响。例如,测试新建成桥梁1 a的频率变化。相对环境因素,因素
,需长时间对健康状态下的结构进行测试,以充分反映环境因素对结构动力特征的影响。例如,测试新建成桥梁1 a的频率变化。相对环境因素,因素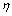 的影响较小。
的影响较小。 可由残差
可由残差 来表示:
来表示:
 (8)
(8)
式(7)可写成:
 (9)
(9)
令样本矩阵 ,其列向量是在测试期
,其列向量是在测试期 时段内的n维样本。样本矩阵Y的协方差为
时段内的n维样本。样本矩阵Y的协方差为
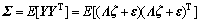 (10)
(10)
式中:E为数学期望。由于 为零均值,
为零均值, <<
<<  ,式(10)可写为
,式(10)可写为
 (11)
(11)
式中: 为残差
为残差 的协方差矩阵。基于式(11)可将样本协方差分解成环境因素成分和残差成分。
的协方差矩阵。基于式(11)可将样本协方差分解成环境因素成分和残差成分。
对样本矩阵Y的协方差矩阵进行奇异值分解:
 (12)
(12)
 ,
,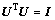 (13)
(13)
式中:U为正交矩阵,其第i个列向量对应第i个主成分,并张成数据子空间;S为奇异值矩阵,矩阵中 越大,说明第i个主成分反映样本的信息越多。矩阵S由S1和S2组成,
越大,说明第i个主成分反映样本的信息越多。矩阵S由S1和S2组成,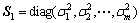 ,
, ,都是对角矩阵。矩阵中的元素是奇异值的平方,并按降序排列,且S2中的元素远小于S1的元素。
,都是对角矩阵。矩阵中的元素是奇异值的平方,并按降序排列,且S2中的元素远小于S1的元素。
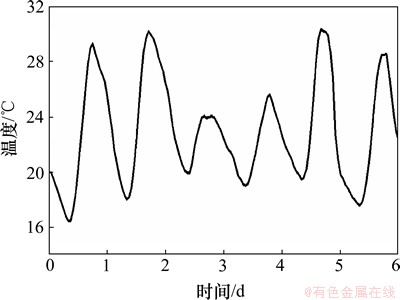
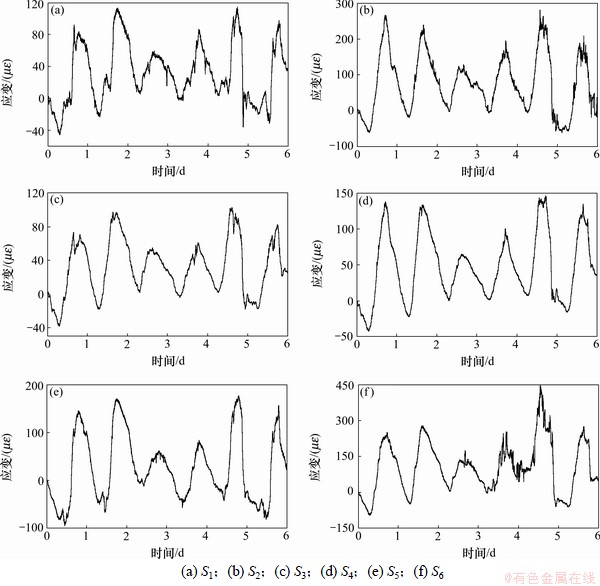
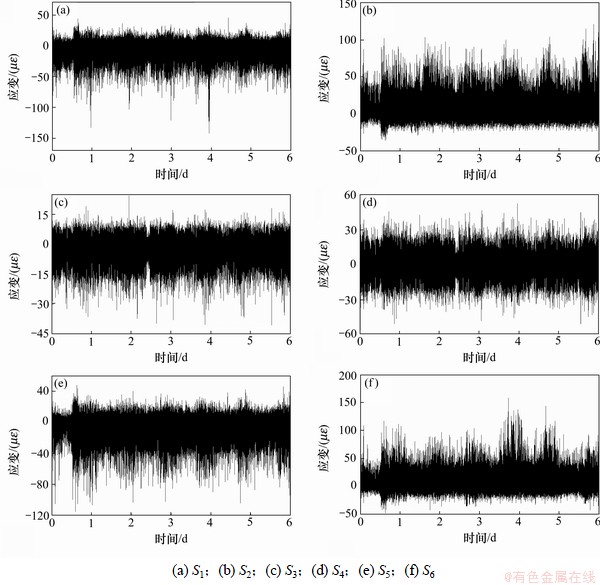
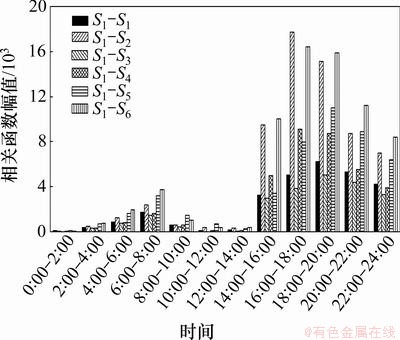
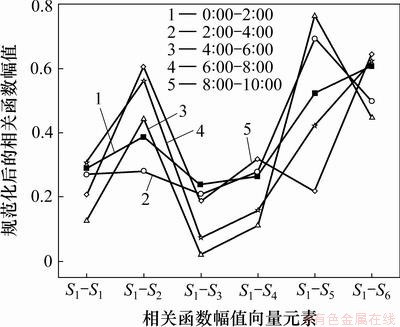
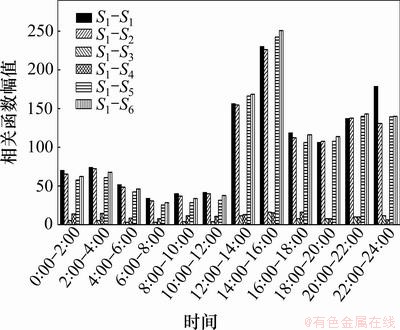
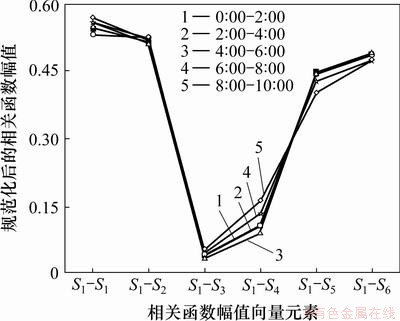
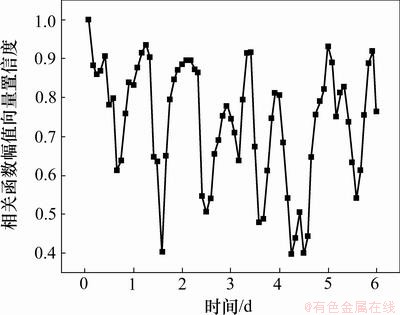
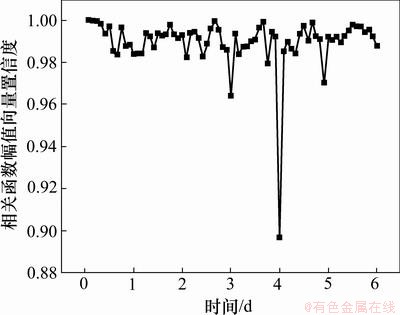
在实际应用中,往往不是取全部的n个主成分,而是只取前m (m 式中:参数m的最小值需要保证I应大于门槛值,一般根据工程实际选取,通常要求I不小于85%。门槛值说明前m个不可观测因素导致样本e的变动程度。从几何的角度来解释,就是样本数据主要沿前m个主成分的方向变化,即样本数据主要分布在前m个主成分组成的子空间内,此环境因素是桥梁结构固有频率改变的主要原因[15],对于频率样本,m可取为1。相应地,矩阵U也可分为2部分: 式中:U1由矩阵U中前m个列向量构成。 为消除运营条件和环境因素的影响,不可观测因素 基于奇异值分解的性质( 根据式(19),式(9)可表示为 由式(20)可知:环境因素对样本Y的影响可剔除。 3 试验数据分析 分析采用的动态应变数据来自某悬索桥跨中上游上弦杆(S1)、上游下弦杆(S2)、上游竖杆(S3)、上游斜杆(S4)、下游上弦杆(S5)和下游下弦杆(S6)6个测点,共6天(4月26日至5月1日)的数据量,测点原始应变时程如图2所示。 环境温度时程曲线见图3。与环境温度时程曲线相比,应变时程表现相似的波动形式。应变时程中包括温度效应信息和活荷载信息。若不考虑温度变化对应变时程的影响,直接采用所测的原始应变数据构造相关函数幅值向量,考虑互其向量中各元素的比例是否仍比较固定,CcorV能否用来判断结构的工作状态,采用2类应变数据进行对比分析:第1类数据反映了测点的原始应变时程;第2类数据去除了温度效应成分,主要反映活荷载信息的应变时程。 3.1 应变时程温度效应成分的提取 对S1~S6测点2011-04-26的原始数据作为样本进行主成分分析,将各测点响应分割成N段长度为n的应变时程样本,组成 图2 测点原始应变时程曲线 Fig.2 Relationship between measured strain history and time 图3 环境温度时程曲线 Fig.3 Relationship between environmental temperature and time 分别对各测点6 d的数据构造样本矩阵,根据式(19),通过第1主成分特征向量对应变数据进行重构,得到如图5所示的应变时程趋势成分。从原始应变时程去除趋势成分后,应变时程主要反映了由活载引起的应变变化,不再呈现类似温度曲线的波动形式,见图6。这也说明:提取出的趋势成分主要为原始应变时程中的温度效应成分。 3.2 相关函数幅值向量分析 动应变相关函数幅值向量的计算步骤如下。 (1) 对各测点6 d的数据(原始应变时程或活载效应成分)按2 h时长分段,每个测点得到72段数据样本。 (2) 以测点S1作为参考点,计算各时段数据样本的相关函数 (3) 求得各时段相关函数的最大绝对值,记为幅值 i=1, 2, …, 72 图4 测点S1~S6样本协方差矩阵的主成分特征值 Fig.4 Principal component eigenvalue of sample covariance matrix of S1-S6 图5 测点S1~S6应变时程的温度效应成分 Fig.5 Composition of temperature effect in measured strain history of S1-S6 2011-04-26全天原始应变时程相关函数见图7。从图7可见:各时段的幅值差别较大。对各时段的幅值向量进行规范化处理后,幅值向量未表现出比较固定的比例形式,见图8(仅给出0:00—10:00时的曲线),这意味着桥梁结构可能出现了损伤。显然,该结果与桥梁的实际工作状况不符。 与原始应变时程相比,活载效应成分(2011-04-26)的相关函数幅值总体偏小。活载成分主要反映的是车载下的应变变化,根据各时段相关函数幅值可判断。活载效应成分的相关函数幅值向量见图9。从图9可见:12:00—24:00时段内桥上的车辆荷载较0:00—12:00时段大。活载效应成分规范化后的相关函数幅值向量见图10(仅给出0~10时的曲线)。从图10可见:经规范化处理后得到一系列比例形式较一致的曲线,说明全天12个时段内,活载效应成分相关函数幅值向量中各元素的比例比较接近。 通过以上分析可知:温度的变化会导致不同时段相关函数幅值向量中元素的比例发生改变,通过式(4)计算相关函数幅值向量置信度CcorV来进一步了解元素比例的变化程度。以2011-04-26 0:00—2:00时段的原始应变响应相关函数幅值向量作为对比基准corVr,计算其余时段样本的corV与基准corVr的置信度,结果如图11所示。从图11可见:置信度在6 d之内变化幅度近60%。同样以26日0:00—2:00时段的活载效应成分建立对比基准,结果如图12所示。从图12可见:各时段的置信度稳定在0.88以内,变化幅度不超过12%。说明基于活载效应成分构造的相关函数幅值向量在长时间内保持了较一致的比例线形;剔除温度效应后,相关函数幅值向量能够反映结构特征,因此,可用于损伤判断建模等。 图6 测点S1~S6应变时程的活载效应成分 Fig.6 Composition of live load effect in measured strain history of S1-S6 图7 原始应变时程的相关函数幅值向量 Fig.7 corV of measured strain history 图8 原始应变时程规范化后的相关函数幅值向量 Fig.8 Normalized corV of measured strain history 图9 活载效应成分的相关函数幅值向量 Fig.9 corV of composition of live load effect 图10 活载效应成分规范化后的相关函数幅值向量 Fig.10 Normalized corV of composition of live load effect 图11 原始应变时程的相关函数幅值向量置信度 Fig.11 CcorV of measured strain history 图12 活载效应成分的相关函数幅值向量置信度 Fig.12 CcorV of composition of live load effect 4 结论 (1) 对实测数据进行主成分分析,第1主成分的累计贡献率都超过95%,通过第1主成分特征向量对实测数据进行重构所得的应变时程呈现出与温度时程相似的波动现象,说明第1主成分主要反映了动应变时程中与温度变化相关的成分信息,主成分分析法可有效提取出应变时程中的温度效应成分。 (2) 实测数据的相关函数幅值向量置信度在0.4~1.0范围内波动;剔除温度效应成分后,置信度稳定在0.88以内。应变时程中的温度效应成分会导致相关函数幅值向量的比例线形发生改变;不考虑环境温度对动应变相关函数幅值向量的影响,易对桥梁结构的健康状况产生误判。 参考文献: [1] 于哲峰, 杨智春. 相关函数幅值向量及其在结构损伤检测中的应用[J]. 机械科学与技术, 2006, 25(1): 24-27. YU Zhefeng, YANG Zhichun. Correlation function amplitude vector and its application to structural damage detection[J]. Mechanical Science and Technology, 2006, 25(1): 24-27. [2] 于哲峰, 杨智春, 舒忠平. 基于互相关函数幅值向量的结构损伤检测实验研究[J]. 机械科学与技术, 2006, 25(11): 1264-1267. YU Zhefeng,YANG Zhichun, SHU Zhongping. Experimental study of structural damage detection using cross correlation function amplitude vectors[J]. Mechanical Science and Technology, 2006, 25(11): 1264-1267. [3] 雷家艳, 姚谦峰, 雷鹰, 等. 基于随机振动响应互相关函数的结构损伤识别试验分析[J]. 振动与冲击, 2011, 30(8): 221-224. LEI Jiayan, YAO Qianfeng, LEI Ying, et al. Structural damage detection method based on correlation function analysis of vibration measurement data[J]. Journal of Vibration and Shock, 2011, 30(8): 221-224. [4] Doebling S W, Farrar C R. Using statistical analysis to enhance modal-based damage identification[C]//Proc DAMAS 97: Structural damage assessment using advanced signal processing procedures. Sheffield: University of Sheffield, 1997: 199-210. [5] Askegaard V, Mossing P. Long term observation of RC-bridge using changes in natural frequencies[J].Journal of Nordic Concrete Research, 1988(7): 20-27. [6] Liu C Y, de Wolf J T. Effect of temperature on modal variability of a curved bridge under ambient loads[J]. Journal of Structural Engineering, 2007, 133(12): 1742-1751. [7] Moser P, Moaveni B. Environmental effects on the identified natural frequencies of the Dowling Hall Footbridge[J]. Mechanical Systems and Signal Processing, 2011, 25(7): 2336-2357. [8] Zhao J, de Wolf J T. Dynamic monitoring of steel girder highway bridge[J]. Journal of Bridge Engineering, ASCE, 2002, 7(6): 350-356. [9] Xia Y, Hao H, Zanardo G, et al. Long term vibration monitoring of an RC slab: Temperature and humidity effect[J]. Engineering Structures, 2006, 28: 441-452. [10] 丁幼亮, 李爱群, 耿方方. 考虑环境因素影响的悬索桥整体状态预警方法[J]. 东南大学学报: 自然科学版, 2010, 40(5): 1052-1056. DING Youliang, LI Aiqun, GENG Fangfang. Monitoring and warning of health conditions for suspension bridges under varying environmental conditions[J]. Journal of Southeast University: Natural Science Edition, 2010, 40(5): 1052-1056. [11] 林友勤, 任伟新. 基于随机状态空间模型的工程结构损伤检测[J]. 振动工程学报, 2007, 20(6): 599-604. LIN Youqin, REN Weixin. Stochastic state space model-based damage detection of engineering structures[J]. Journal of Vibration Engineering, 2007, 20(6): 599-604. [12] Magalhaes F, Cunha A, Caetano E. Vibration based structural health monitoring of an arch bridge: From automated OMA to damage detection[J]. Mechanical Systems and Signal Processing, 2012, 28: 212-228. [13] Farrar C R, Baker W E, Bell T M, et al. Dynamic characterization and damage detection in the I-40 bridge over the rio grande[R]. New Mexico (United States): Los Alamos National Lab, 1994: 48-51. [14] Deraemaeker A, Reynders E, Roeck G D, et al. Vibration-based structural health monitoring using output-only measurements under changing environment[J]. Mechanical Systems and Signal Processing, 2008, 22(1): 34-56. [15] Yan A M, Kerschen G, Boe P D, et al. Structural damage diagnosis under varying environmental conditions-Part I: A linear analysis[J]. Mechanical Systems and Signal Processing, 2005, 19(4): 847-864. (编辑 陈灿华) 收稿日期:2012-08-12;修回日期:2012-10-23 基金项目:国家自然科学基金资助项目(51078357) 通信作者:李苗(1980-),男,湖南益阳人,博士研究生,从事桥梁健康监测研究;电话:15974268771;E-mail: lm_hncu@163.com (14)
(14) (15)
(15) 和
和 可通过U1和U2来确定:
可通过U1和U2来确定: (16)
(16)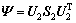 (17)
(17)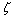 在最小二乘法最小化
在最小二乘法最小化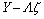 的条件下可由下式估算得到:
的条件下可由下式估算得到: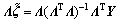 (18)
(18)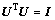 ),式(18)可进一步写成:
),式(18)可进一步写成: (19)
(19)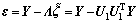 (20)
(20) 是数据的重构,
是数据的重构, 是将样本映射至主要反映环境因素信息的空间;
是将样本映射至主要反映环境因素信息的空间; 是将样本Y从环境特征子空间重映射至原始数据空间,这个过程完成了对样本Y中环境影响成分的提取。
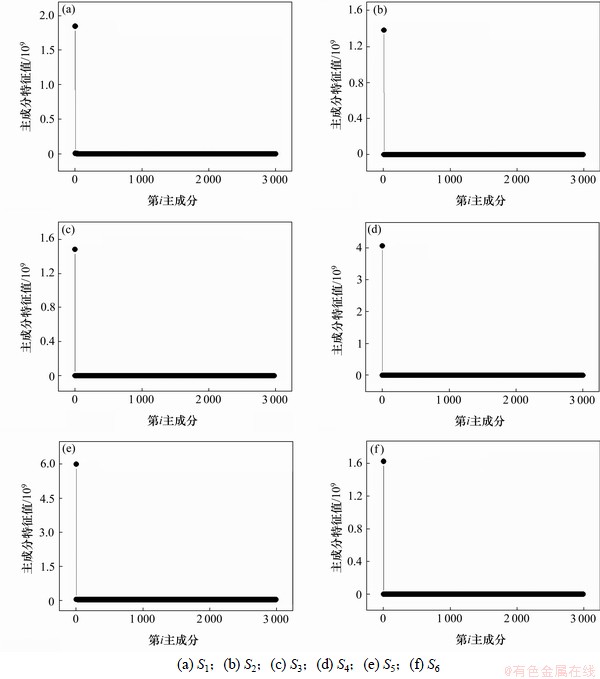
是将样本Y从环境特征子空间重映射至原始数据空间,这个过程完成了对样本Y中环境影响成分的提取。 的样本矩阵。这里取5 min时长的应变时程作为样本矩阵里的1列数据,24 h的数据被分为288段。S1~S6测点样本协方差矩阵的主成分特征值分布如图4所示,根据式(14)分别计算第1主成分的累计贡献率为95.592%,99.367%,99.704%,99.408%,98.534%和99.397%,说明第1主成分反映了动应变时程绝大部分的波动信息。
的样本矩阵。这里取5 min时长的应变时程作为样本矩阵里的1列数据,24 h的数据被分为288段。S1~S6测点样本协方差矩阵的主成分特征值分布如图4所示,根据式(14)分别计算第1主成分的累计贡献率为95.592%,99.367%,99.704%,99.408%,98.534%和99.397%,说明第1主成分反映了动应变时程绝大部分的波动信息。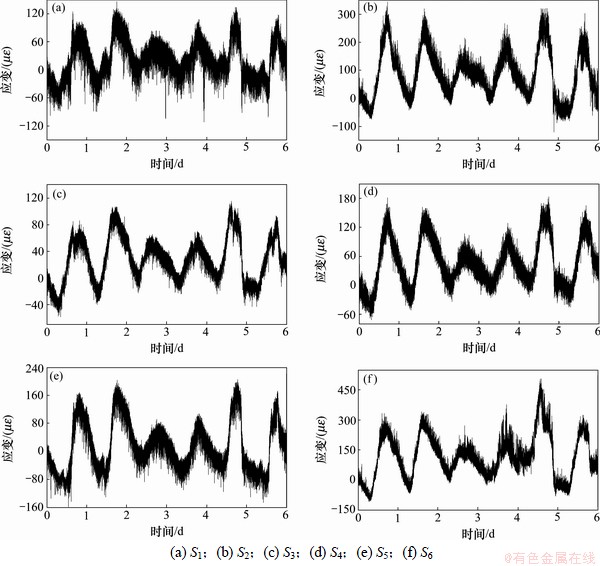
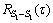 ,
, ,
,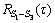 ,
,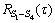 ,
, 和
和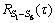 。
。 ,形成相关函数幅值向量corV:
,形成相关函数幅值向量corV: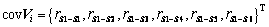 ;
;
摘要:分析变温度下实测动应变相关函数幅值向量的变化情况。采用基于主成分分析的环境温度影响剔除方法,寻找主要反映应变时程温度信息的特征子空间。对时程数据重构,得到温度效应成分,由此消除温度对应变信号的影响。研究结果表明:第一主成分反映了动应变时程绝大部分的波动信息;通过第一主成分特征向量可有效提取应变时程中的温度效应成分。基于实测动应变的相关函数幅值向量在各时段的比例形态均存在较大差异,剔除温度效应成分后的相关函数幅值向量呈现一致的比例线形,说明应变时程中的温度效应成分会导致相关函数幅值向量的比例线形发生改变;不考虑环境温度对动应变时程相关函数幅值向量的影响,易对桥梁结构的健康状况产生误判。
[1] 于哲峰, 杨智春. 相关函数幅值向量及其在结构损伤检测中的应用[J]. 机械科学与技术, 2006, 25(1): 24-27.
[2] 于哲峰, 杨智春, 舒忠平. 基于互相关函数幅值向量的结构损伤检测实验研究[J]. 机械科学与技术, 2006, 25(11): 1264-1267.
[3] 雷家艳, 姚谦峰, 雷鹰, 等. 基于随机振动响应互相关函数的结构损伤识别试验分析[J]. 振动与冲击, 2011, 30(8): 221-224.
[10] 丁幼亮, 李爱群, 耿方方. 考虑环境因素影响的悬索桥整体状态预警方法[J]. 东南大学学报: 自然科学版, 2010, 40(5): 1052-1056.
[11] 林友勤, 任伟新. 基于随机状态空间模型的工程结构损伤检测[J]. 振动工程学报, 2007, 20(6): 599-604.


