Trans. Nonferrous Met. Soc. China 28(2018) 2314-2323

Distribution of stress and strain between adjacent particles in particulate reinforced metal matrix composites

Qing LIU, Fu-gong QI, Hai-min DING, Xiao-liang FAN, Ying YUE

School of Energy, Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China

Received 11 September 2017; accepted 28 February 2018

Abstract:

The distribution of stress and strain between adjacent particles in particulate reinforced metal matrix composites was investigated using cohesive zone models. It is found that the strain of the composite is concentrated in the matrix, and there is a region with higher strain along the loading path, which can promote the formation of a void near the particles pole. The stress and strain in matrix near the particles gradually decrease with the increase of the distance between particles. And it is calculated that there is a critical distance within which the stress and strain fields of the neighboring particles can influence with each other. This critical distance increases with the increase of particle size. It is also found that the angle between the tensile direction and the center line of particles plays an important role in the stress and strain distribution. The model with the angle of 0° has the greatest influence on the distribution of stress and strain in the matrix, while the model with the angle of 45° has the least influence on the distribution of stress and strain in the matrix.

Key words:

stress; strain; metal matrix composite; finite-element analysis; fracture; interface;

1 Introduction

Particulate reinforced metal matrix composites (PRMMCs), a sub-group of metal matrix composites (MMCs), have received substantial attention and have been widely applied in various fields in recent decades because of their excellent properties, such as high specific stiffness and strengths [1-6], outstanding frication and high wear resistance [7-9], high electrical and thermal conductivity [10,11], and high temperature mechanical behavior [12-14]. Also, manufacturing flexibility and cost-effectiveness are two other powerful driving forces for wide-spreading industrial applications of PRMMCs since they can be machined with the majority of traditional manufacturing processes designed for metals [15]. However, the addition of the hard particles will also result in the degradation of ductility, fracture toughness and low-cycle fatigue properties, which limits their application in practice [16].

It is known that the fracture of materials is due to the propagation of cracks, while the stress concentration is the key for the cracks propagation. As for PRMMCs, when the load is applied, there will be stress concentration near interface between the reinforced particle and matrix, which will make the interface weak and result in the cracks propagation from there. Therefore, figuring out the distribution of stress as well as strain near the interface during the loading process is important for understanding the fracture behavior of PRMMCs.

Simulation method has been widely used to study the distribution characteristic of stress and strain in the PRMMCs in recent years. For example, YUAN et al [17] have proved that the particle shape and interface geometry play an important role in the distribution of stress state. Moreover, particles with a larger aspect ratio and perpendicular to tensile loading direction are easy to crack, while those with a smaller aspect ratio are prone to interface debonding from particle poles. MENG and WANG [18] used a micromechanical model based on the cohesive zone model to analyze the interfacial failure mechanisms in PRMMCs. They studied the effect of interfacial properties on the tensile behavior of composite and considered that a complete interfacial debonding all over the particles could never be reached, and the plastic strain of composite shows an increase trend with strengthening the interfacial strength. WILLIAMS et al [19] and SU et al [20] performed similar multi-particle 3D models to investigate the relationship between the mechanical behavior and composite structure.

For the time being, during studying the distribution of stress and strain near the interface in PRMMCs by the simulation method, the model with an individual particle is commonly used. However, it is noticed that the particles distance can be very short in PRMMCs with high particle volume fraction, while, even in PRMMCs with low particle volume fraction, the particle distance may also be very short due to the particle aggregation. In these cases, the stress and strain fields of adjacent particles will inevitably interact with each other, which will change the whole distribution of stress and strain near the interface and ultimately influence the mechanical properties, especially the fracture behavior of PRMMCs.

Therefore, in this work, based on a cohesive zone model, the widely used SiC particle-reinforced Al matrix composite was chosen as the model system to study the distribution of stress and strain between adjacent particles in PRMMCs. It is considered that the results are useful for understanding the influence of particle distribution on the fracture behavior and helpful for improving the fracture toughness of PRMMCs.

2 Modeling and simulation

In order to develop an appropriate finite element to analyze the distribution of stress and strain between adjacent particles in PRMMCs, a two-dimensional model is proposed with a special design of matrix (Al) and reinforced particle (SiC), as shown in Fig. 1. Referring to Fig. 1(a), in order to study the influence between the particles, the analysis model is built with two particles embedding in finite matrix. The length and width of the matrix are set to be 120 μm after essential tests. The radius of reinforced particles is 5 μm in all the studies except the study of the influence of particle size in which the radii are 5, 2.5, 1 and 0.5 μm, respectively. In addition, the distance between particles A and B (the distance is designated to be D in the following) is set in a suitable range according to the particle size and the angle between the tensile direction and the center line of the particles (the angle is designated to be α) which is set to be 0°, 30°, 45°, 60° and 90°, respectively. In those models, the material parameters of the elastic particle and elastic-plastic matrix are shown in Table 1. Figure 1(b) shows one of the constructed models (D=60 μm, α=0°) which is similar to others. The models are meshed with an eight-node element (PLANE183, 2D structural element, ANSYS). The meshes are made finer near particle/matrix interfaces. In order to get time-saving and convergent calculation, the mesh density is set to be reasonable as far as possible after several attempts and contrasts. Moreover, cohesive zone model [21,22] is employed to simulate the interface of particles and matrix.

Fig. 1 Analysis model (a) and finite element mesh for calculation model (b)

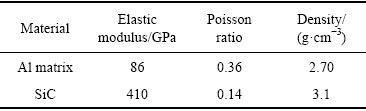
Table 1 Material parameters of SiC particle and Al matrix

DANDEKAR and SHIN [23] have proposed a traction-separation law for an aluminum-silicon carbide composite system by conducting molecular dynamics simulation. In this study, the ANSYS element type of INTER203 is chosen and the parameters are set according to the simulation by DANDEKAR and SHIN [23], as shown in Fig. 2.

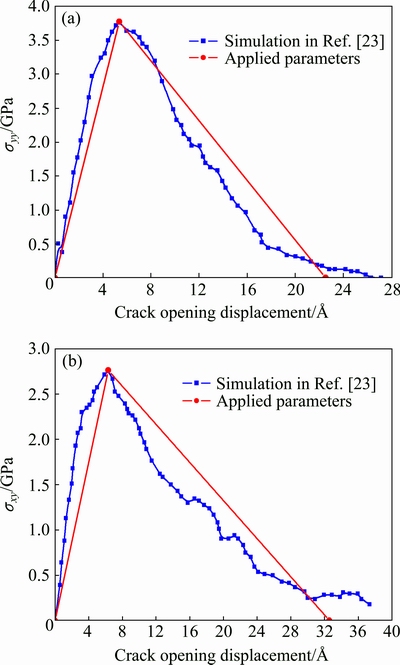
Fig. 2 Traction-separation relationship for model Ⅰ (a) and model Ⅱ (b) failure at Al/SiC interface (σ_yy and σ_xy are tensile and shear traction stress, respectively)

The boundary conditions (BCs) also play an important role in the simulated results. The uniaxial tensile behavior of particle-reinforced composites is mainly studied in this work. Considering the actual situation, boundary conditions are set as follows:

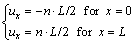                      (1)

where u_x is the component of the displacement vector u along x-direction, n is the specific displacement coefficient to the x-direction, and it is set to be 1% in all the study, L is the length of the cubic model, which is settled to be 120 μm. In brief, the boundary conditions mean that the lines x=0 and x=L are maintained straight and move parallel with respect to its original shapes under loading.

3 Results and discussion

3.1 Stress and strain field distribution around reinforced particles

In PRMMCs, different properties between particle and matrix and their good combination give rise to the excellent performance of the composites. However, the differences between particle and matrix also make the stress and strain field distribution different in various parts of the composites and then result in the complicated transformation and failure behavior. Taking Al/SiC composite as an example, the elastic modulus of SiC is about five times greater than that of aluminum, and the Poisson ratio and density are different either. As a result, the Al matrix and SiC particles would share the stress and strain differently under the load. Figures 3 and 4 show the strain and stress distribution of Al matrix composite reinforced by SiC particles with the radius of 5 μm and the distance between the two particles of    60 μm.

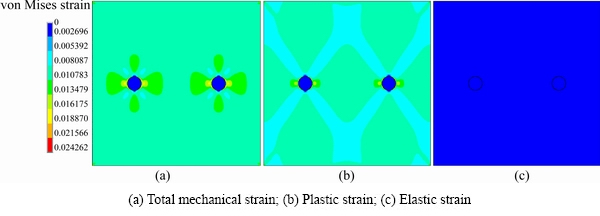
Fig. 3 von Mises strain contours of sample

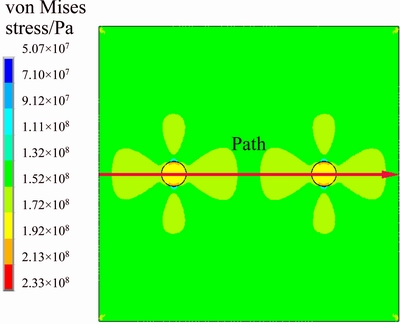
Fig. 4 von Mises stress contour of sample

Figure 3 shows the contour plot of von Mises strain generated in the matrix and particles. It can be observed that when the tensile load is applied, the matrix and particle will sustain different strains due to different properties. And higher strains are generated in matrix while the particles have little deformation. At the same time, after the total strain is divided into elastic stain and plastic strain, it is found that the distribution of von Mises total mechanical strain (Fig. 3(a)) is similar to that of von Mises plastic strain (Fig. 3(b)), and the von Mises elastic strain (Fig. 3(c)) is negligibly small. It can be concluded that the deformation of the model is mainly concentrated in the matrix. Moreover, the deformation of the matrix near the particle promotes the formation of a void at the pole, which is in a good agreement with experimental results in Ref. [24]. As for the stress distribution, it is found that, in the matrix, the stress is higher around the path (as shown in Fig. 4) which is parallel to the tensile load.

In addition, in order to get further understanding of the stress and strain distribution near the interface, the strain and stress scatter diagrams of particle A in spherical coordinates are obtained and shown in Fig. 5. It can be seen that, like the results shown in Figs. 3 and 4, the reinforced particle has little deformation, while the matrix undergoes large deformation. Obviously, the strain and stress have significant changes near the interface.

Referring to Figs. 3 and 4, it can be seen that the stress and strain change quickly on the path. The von Mises stress and strain curves along the path are obtained and shown in Fig. 6. In Fig. 6(b), it can be observed that the stress has a large fluctuation at interface which can easily lead to interface debonding. Moreover, the stress of particle is obviously larger than that in matrix. Therefore, it is deduced that, although the SiC particle has high elastic modulus, the stress concentration on particles is also potential inducement to material failure. The above deductions are in accordance with those in the work of KANETAKE et al [24], which have proved that interface debonding and reinforced particle cracking are the two primary ways for the failure of PRMMCs.

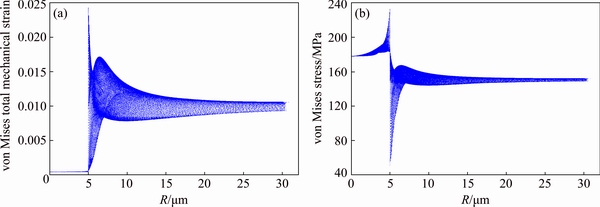
Fig. 5 Scatter diagrams of von Mises total mechanical strain (a) and von Mises stress (b) of near particle A under spherical coordinate system

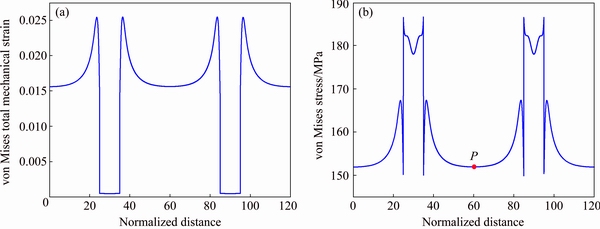
Fig. 6 von Mises total mechanical strain (a) and von Mises stress (b) curves on path

It is also found from Fig. 6 that the stress and strain in matrix near the particle gradually decrease with increasing the distance from the particle. Moreover, the strain and stress have a rapid decline near the interface while the changes tend to be gentle as a further distance from interface. In order to further research the stress distribution, the minimum point between the two particles on the stress curve is set as point P in the following sections, as shown in Fig. 6(b).

3.2 Influence of interaction between adjacent particles with different distances, particle sizes and loading directions on distribution of stress and strain near interface

Many works have found that the particle size, volume fraction and distribution will influence the fracture toughness of PRMMCs [25-30]. As mentioned above, the fracture behavior is closely related with the stress distribution, especially stress concentration. Therefore, in order to clarify the influence mechanism of the particle size, volume fraction and distribution on fracture toughness, in the following work, the influence of the reinforced particles with different distances, particle sizes and loading directions on the distribution of stress and strain near the interface in PRMMCs has been studied.

At first, the influence of different distances between two particles (D) on stress and strain distribution is analyzed and the results can be used to examine the influence of volume fraction. The distribution of the two particles is parallel to tensile load. The models with particle size of 5 μm and several different distances from 16 to 65 μm are studied, respectively. The change of the distance is obtained by the movement of particle B while the position of particle A is fixed.

Figure 7 shows the strain and stress distribution of the models with distances of 16, 35 and 65 μm, respectively. As shown in Figs. 7(a) and (d), the strain and stress of the matrix between the two particles are the highest in the model with the distance of 16 μm. And it can be concluded that the strain and stress of the matrix between two particles decrease with the increase of the distance, and the influence between the two particles will be negligibly small when the distance is large enough.

Furthermore, the strain and stress curves along the path (as shown in Fig. 4) are shown in Fig. 8. Figure 8(a) presents the strain curves along the path in the models with distances of 16, 20, 35, 50 and 65 μm, respectively. It can be found that the particles have little deformation while the strain in the matrix has a large fluctuation with the location of a strain peak at the interface. This shows that the interface is a failure prone position which further confirms the experimental result in Ref. [24]. And the strain in the matrix gradually increases with the decrease of the distance from the interface. In addition, it is noticed that the strain in the matrix between particles increases with the decrease of the distance between the two particles. However, the strain of the particle is stable at a low level with those changes. According to the results shown in Fig. 8(b), like the results mentioned above, the stress of the particle is greater than that of the matrix. There is a leap of the stress curve at the interface, indicating the serious stress concentration of the  interface. With shortening the particle distance, the stresses of both particles and the matrix between the two particles have a increasing trend, especially with the distance from 35 to 16 μm.

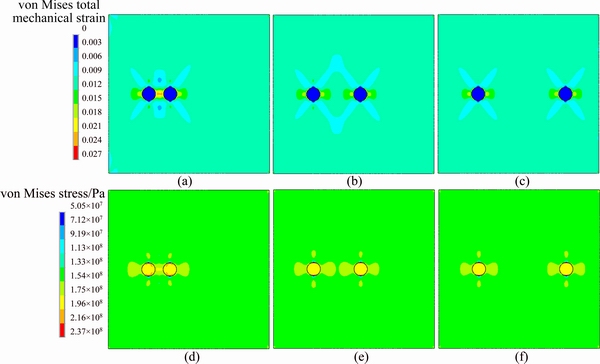
Fig. 7 von Mises total mechanical strain contours at particle distances of 16 μm (a), 35 μm (b), and 65 μm (c), and von Mises stress at particle distances of 16 μm (d), 35 μm (e), and 65 μm (f)

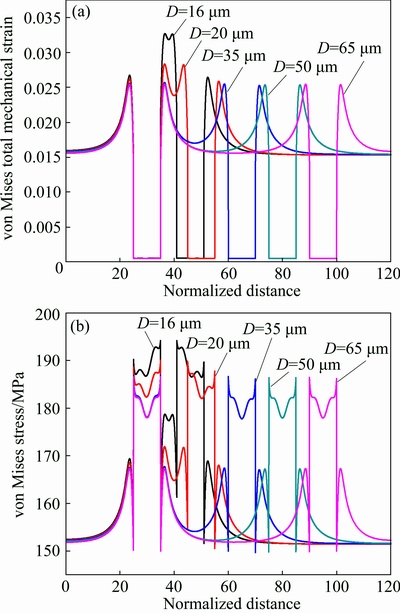
Fig. 8 von Mises total mechanical strain (a) and von Mises stress (b) on path with different particle distances

Actually, various distances between particles can imply the clustering degree of the particles in matrix. Namely, the clustering degree will increase with the decrease of the distance between particles. Obviously, it can be observed from Fig. 8 that the strain and stress between particles increases when the particle distance is shortened, and the stress of particles markedly increases. Therefore, in a composite with inhomogeneously distributed particles, the particle-rich region will share more load than the particle-lean region and this difference will be exacerbated when the particle distribution becomes clustered, which has been reported in Ref. [31].

In addition, PARK et al [16] have found that the cracks propagated through the particle-free regions of matrix perpendicular to the loading direction in the composites with low volume fraction of SiC, while the matrix failed in shear as the volume fraction increased and the distance between the particles decreased. SONG and XIAO [26] also have concluded that the fracture toughness and the tensile ductility decreased as the volume fraction of the SiC particles increased. It is known that, with a given particle size, the change of volume fraction means the change of the distance between particles in the composites. As shown in Figs. 7 and 8, when the distance between the particles is far, which means, in another way, the volume fraction of the particles is small, the stress of particles and interface is small and stable. However, the stress of particles and interface increases progressively with decreasing interparticle spacing, especially the stress at interface. Therefore, the interface becomes failed more easily and leads to the decrease of fracture toughness.

In order to quantify the influence of particle distance, an assumption was proposed with the stress of point P as shown in Fig. 6(b). It is thought that the particles have no influence on each other when the stress of point P is smaller than the threshold value which is designated as 1.005 times the far-field stress. So, the  stress curve of point P with different particle distances is shown in Fig. 9. Based on the above results, it is found that the critical distance of the two particles within which the stress and strain field of the neighboring particles can influence with each other is about 51.18 μm in this Al-SiC composite, which can be considered as the maximum influential distance. In another word, the influence between particles can be ignored when the distance of particles along the tensile direction is larger than 51.18 μm.

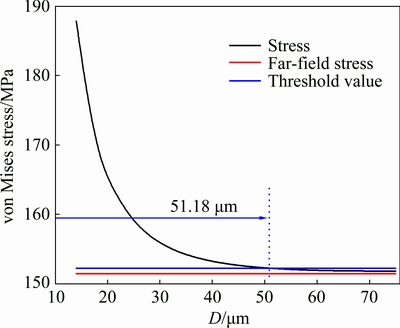
Fig. 9 von Mises stress variation of point P with different particle distances (D) at R_A=5 μm and R_B=5 μm

Then, the influence of particle size on the stress and strain distribution is analyzed. The models with combination of particle sizes of 5, 2.5, 1, and 0.5 μm are studied, respectively. Figure 10 shows the models with the distance between particles of 20 and 40 μm. Similar to Fig. 7, it can be observed that the influence between particles decreases with increasing the distance between particles as shown in Figs. 10(a)-(h). In addition, with the same size of particle A, the distribution of stress near particle A is different due to various sizes of particle B. Undoubtedly, the particle size can influence the stress distribution, and the influence remarkably decreases  with the size diminution of particle B as shown in Figs. 10(h)-(e). Figure 11 shows a further instruction of the influence of particle size with the stress curves. Obviously, the stress between particles decreases with the size diminution of particle B. Also, the stress of particle A has a decreasing trend with the diminution of particle size, as shown in Fig. 11(a). However, the influence of particle size on the stress of particle A is negligibly small when the distance is larger as shown in Fig. 11(b).

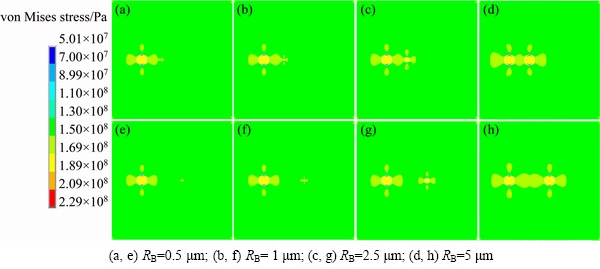
Fig. 10 von Mises stress contours of samples with R_A = 5 μm at D=20 μm (a-d) and D=40 μm (e-h)

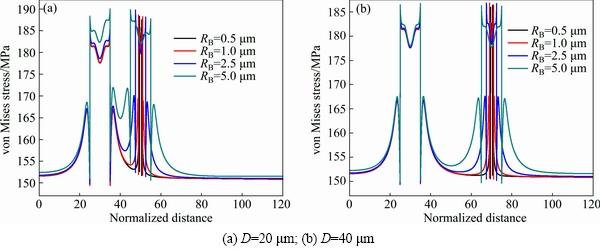
Fig. 11 von Mises stress curves of models with R_A=5 μm and different R_B values

After analyzing various models with different distances and particle sizes and a large amount of data processing, the simulated results of point P are shown in Fig. 12. It can be seen that the maximum influential distance increases with the increase of particle size. Via MATLAB, a simulation of surface by the maximum influential distance showing in Fig. 12 is proposed, as shown in Fig. 13. It clearly shows the variation tendency of the maximum influential distance. The maximum influential distance increases progressively with the increase of particle size, but the rate of increase gradually declines.

The above simulation studies have assumed that the center line of the particles in the model is parallel to the tensile direction. However, there is usually an angle between the tensile direction and the center line of the particles in the practice. So, in order to study the influence of this angle, other four models are built with angles of 30°, 45°, 60° and 90°, respectively. Figure 14 shows the von Mises stress contours of models with particle distances of 20 and 40 μm.

By contrast, it can be concluded that the model with angle of 0° has the greatest influence on the matrix. Moreover, the influence between each other should be the least when the angle is 45°. It can also be seen that the distance between particles has a strong impact on stress distribution, which further confirms the above results.

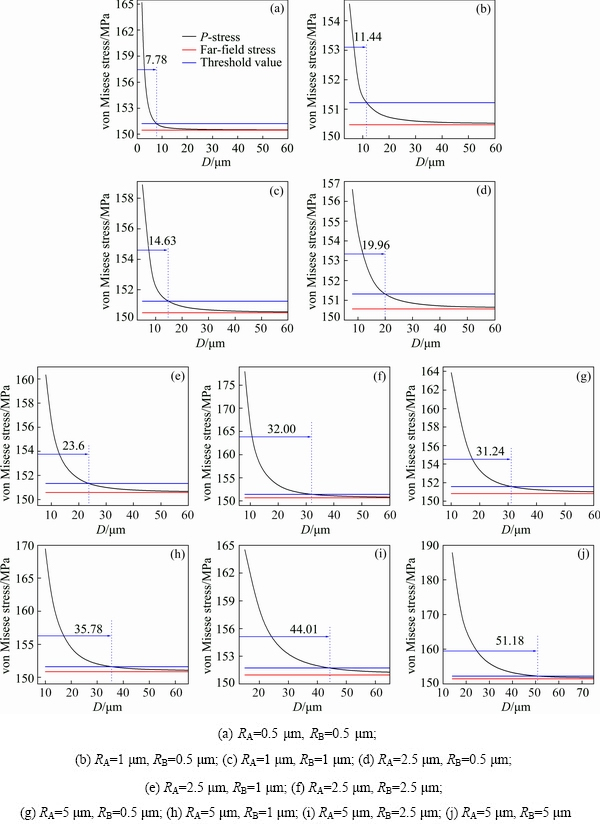
Fig. 12 von Mises stress variations of samples at point P with different particle sizes and distances

Fig. 13 Maximum influential distance with different particle sizes

4 Conclusions

1) The deformation of the composite is concentrated in the matrix under the tensile load, and there is a region with higher strain in the matrix along the loading path, which can promote the formation of a void near the particle poles.

2) The stress and strain in the matrix near the particle gradually decrease from near to far. It is calculated that there exists a critical distance that the stress and strain of the particles influence with each other, and the critical distance increases with the increase of particle size.

3) The loading direction will also influence the distribution of stress and strain, the model with the angle of 0° between the tensile direction and the center line of the particles has the greatest influence on the distribution of stress and strain in the matrix while the model with angle of 45° has the least influence.

Fig. 14 von Mises stress contours of samples at D=20 μm (a-e) and D=40 μm (f-j)

References

[1] HUANG L J, WANG S, GENG L, KAVEENDRAN B, PENG H X. Low volume fraction in situ (Ti₅Si₃+Ti₂C)/Ti hybrid composites with network microstructure fabricated by reaction hot pressing of Ti-SiC system [J]. Composites Science and Technology, 2013, 82: 23-28.

[2] SIVAKUMAR G, ANANTHI V, RAMANATHAN S. Production and mechanical properties of nano SiC particle reinforced Ti-6Al-4V matrix composite [J]. Transactions of Nonferrous Metals Society of China, 2017, 27: 82-90.

[3] WARD P J, ATKINSON H V, ANDERSON P. Semi-solid processing of novel MMCs based on hypereutectic aluminium-silicon alloys [J]. Acta Materialia, 1996, 44: 1717-1727.

[4] JEBEENMOSES J, DINAHARAN I, JOSEPHSEKHAR S. Prediction of influence of process parameters on tensile strength of AA6061/TiC aluminum matrix composites produced using stir casting [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 1498-1511.

[5] QI Q, LIU Y,ZHANG H, ZHAO J, GAI L L, HUANG Y H, HUANG Z R. The formation mechanism of TiC particles in TiC/Ni composites fabricated by in situ reactive infiltration [J]. Journal of Materials Science, 2016, 51(14): 7038-7045.

[6] LI X P, LIU C Y, LUO K, MA M Z, LIU R P. Hot deformation behaviour of SiC/AA6061 composites prepared by spark plasma sintering [J]. Journal of Materials Science & Technology, 2016, 32(4): 291-297.

[7] SHARMAA N K, MISRA R K, SHARMA S. Thermal expansion behavior of Ni-Al₂O₃ composites with particulate and interpenetrating phase structures: An analysis using finite element method [J]. Computational Material Science, 2014, 90: 130-136.

[8] LI J F, ZHANG L, XIAO J K, ZHOU K C. Sliding wear behavior of copper-based composites reinforced with graphene nanosheets and graphite [J]. Transactions of Nonferrous Metals Society of China, 2015, 25: 3354-3362.

[9] JIAO Y, HUANG L J, WANG S, LI X T, AN Q, CUI X P, GENG L. Effects of first-scale TiB_w on secondary-scale Ti₅Si₃ characteristics and mechanical properties of in-situ (Ti₅Si₃+TiB_w)/Ti6Al4V composites [J]. Journal of Alloys and Compounds, 2017, 704: 269-281.

[10] WEBER L, DORN J, MORTENSEN A. On the electrical conductivity of metal matrix composites containing high volume fractions of non-conducting inclusions [J]. Acta Materialia, 2003, 51: 3199-3211.

[11] TENG F, YU K, LUO J, FANG H J, SHI C L, DAI Y L, XIONG H Q. Microstructures and properties of Al-50%SiC composites for electronic packaging applications [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 2647-2652.

[12] XIU Z Y, YANG W S, DONG R H, HUSSAIN M, JIANG L T, LIU Y X, WU G H. Microstructure and mechanical properties of 45 vol.% SiC_p/7075Al composite [J]. Journal of Materials Science & Technology, 2015, 31(9): 930-934.

[13] JESHURUNLIJAY K, RAJASELVAM D J, DINAHARAN I, VIJAY S J. Microstructure and mechanical properties characterization of AA6061/TiC aluminum matrix composites synthesized by in situ reaction of silicon carbide and potassium fluotitanate [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 1791-1800.

[14] MADEIRA S, CARVALHO O, CARNEIRO V H, SOARES D, SILVA F S, MIRANDA G. Damping capacity and dynamic modulus of hot pressed AlSi composites reinforced with different SiC particle sizes [J]. Composites (Part B): Engineering, 2016, 90: 399-405.

[15] GARCIA I G, MANTIC V, GRACIANI E. A model for the prediction of debond onset in spherical-particle-reinforced composites under tension: Application of a coupled stress and energy criterion [J]. Composites Science & Technology, 2015, 106: 60-67.

[16] PARK B G, CROSKY A G, HELLIER A K. Fracture toughness of microsphere Al₂O₃-Al particulate metal matrix composites [J]. Composites (Part B): Engineering, 2008, 39: 1270-1279.

[17] YUAN Z W, LI F G, XUE F M, HE M, HUSSAIN M Z. Analysis of the stress states and interface damage in a particle reinforced composite based on a micromodel using cohesive elements [J]. Materials Science and Engineering A, 2014, 589: 288-302.

[18] MENG Q H, WANG Z Q. Prediction of interfacial strength and failure mechanisms in particle-reinforced metal-matrix composites based on a micromechanical model [J]. Engineering Fracture Mechanics, 2015, 142: 170-183.

[19] WILLIAMS J J, SEGURADO J, LLORCA J, CHAWLA N. Three dimensional (3D) microstructure-based modeling of interfacial decohesion in particle reinforced metal matrix composites [J]. Materials Science and Engineering A, 2012, 557: 113-118.

[20] SU Y S, OUYANG Q B, ZHANG W L, LI Z Q, GUO Q, FAN G L, ZHANG D. Composite structure modeling and mechanical behavior of particle reinforced metal matrix composites [J]. Materials Science and Engineering A, 2014, 597: 359-369.

[21] PARK K, PAULINO G H. Cohesive zone models: A critical review of traction-separation relationships across fracture surfaces [J]. Applied Mechanics Reviews, 2011, 64(6): 060802.

[22] YUAN Z F, FISH J. Are the cohesive zone models necessary for delamination analysis? [J]. Computer Methods in Applied Mechanics and Engineering, 2016, 310: 567-604.

[23] DANDEKAR C R, SHIN Y C. Molecular dynamics based cohesive zone law for describing Al-SiC interface mechanics [J]. Composites (Part A): Applied Science and Manufacturing, 2011, 42: 355-363.

[24] KANETAKE N, NOMURA M, CHOH T. Continuous observation of microstructural degradation during tensile loading of particle reinforced aluminium matrix composites [J]. Materials Science & Technology, 1995, 11: 1246-1252.

[25] JAMALI M, FAROKHZADEH K, BAGHERI R, REIHANI S M S. Architecturally modified Al-DRA composites: The effect of size and shape of the DRA rods on fracture behavior [J]. Journal of Materials Science, 2010, 45(11): 2852-2861.

[26] SONG M, XIAO D H. Modeling the fracture toughness and tensile ductility of SiC_p/Al metal matrix composites [J]. Materials Science and Engineering A, 2008, 474: 371-375.

[27] WANG Z W, SONG M, SUN C, HE Y H. Effects of particle size and distribution on the mechanical properties of SiC reinforced Al-Cu alloy composites [J]. Materials Science and Engineering A, 2011, 528: 1131-1137.

[28] HU J, WU G H, ZHANG Q, GOU H S. Mechanical properties and damping capacity of SiC_p/TiNi_f/Al composite with different volume fractions of SiC particle [J]. Composites (Part B): Engineering, 2014, 66: 400-406.

[29] SONG M, HUANG B Y. Effects of particle size on the fracture toughness of SiC_p/Al alloy metal matrix composites [J]. Materials Science and Engineering A, 2008, 488: 601-607.

[30] CHEN J, BAO C G, CHEN W H, ZHANG L, LIU J L. Mechanical properties and fracture behavior of Mg-Al/AlN composites with different particle contents [J]. Journal of Materials Science & Technology, 2017, 33(7): 668-674.

[31] CONLON K T, WILKINSON D S. Effect of particle distribution on deformation and damage of two-phase alloys [J]. Materials Science and Engineering A, 2001, 317: 108-114.

颗粒增强金属基复合材料近邻颗粒间的应力及应变分布

柳 青，祁复功，丁海民，范孝良，乐 英

华北电力大学 能源动力与机械工程学院，保定 071003

摘  要：采用内聚力模型研究颗粒增强金属基复合材料近邻颗粒间的应力及应变分布。结果表明，复合材料的应变主要集中于基体上，在加载路径上存在一个应变较高的区域，从而促进了颗粒极点附近空洞的形成。基体的应力和应变都随着基体与增强颗粒距离的增大而减小。模拟结果表明，增强颗粒之间的相互影响有一个临界距离，而且这个临界距离会随粒径的增大而增大。此外，加载方向和颗粒的中心线夹角对应力和应变的分布也有一定的影响，当加载方向和颗粒的中心线夹角为0°时，颗粒之间的相互影响最大，其夹角为45°时颗粒之间的相互影响最小。

关键词：应力；应变；金属基复合材料；有限元分析；断裂；界面

(Edited by Wei-ping CHEN)

Foundation item: Project (51301068) supported by the National Natural Science Foundation of China; Project (E2014502003) supported by the Natural Science Foundation of Hebei Province, China; Project (2018MS120) supported by Fundamental Research Fund for the Central Universities, China

Corresponding author: Qing LIU; Tel: +86-312-7525433; E-mail: 52452061@ncepu.edu.cn

DOI: 10.1016/S1003-6326(18)64876-9

Abstract: The distribution of stress and strain between adjacent particles in particulate reinforced metal matrix composites was investigated using cohesive zone models. It is found that the strain of the composite is concentrated in the matrix, and there is a region with higher strain along the loading path, which can promote the formation of a void near the particles pole. The stress and strain in matrix near the particles gradually decrease with the increase of the distance between particles. And it is calculated that there is a critical distance within which the stress and strain fields of the neighboring particles can influence with each other. This critical distance increases with the increase of particle size. It is also found that the angle between the tensile direction and the center line of particles plays an important role in the stress and strain distribution. The model with the angle of 0° has the greatest influence on the distribution of stress and strain in the matrix, while the model with the angle of 45° has the least influence on the distribution of stress and strain in the matrix.