大地电磁二维正演中的有限元-径向基点插值法-有色金属在线

径向基点插值法(RPIM)作为一种插值型无网格方法，为改善无网格点插值法(PIM)在形函数构造过程中可能出现的矩阵奇异性问题而提出的一种方法，该算法支持域无量纲尺寸的选择区间大，能更好地处理各类工程与科学计算问题。介绍了RPIM的近似原理，给出了径向基函数形状参数的推荐值；从大地电磁二维变分问题出发利用Galerkin法结合高斯积分公式推导出相应的系统矩阵离散表达式；为提高RPIM的计算效率，将RPIM与有限元法(FEM)耦合，提出了有限元－径向基点插值法(FE-RPIM)，多个模型的数值计算验证了RPIM精度高、处理复杂模型便利及耦合法计算复杂模型高效的特点。

关键词：

径向基点插值法；有限元；无网格方法；大地电磁；

中图分类号：P631　　文献标志码：A

Magnetotelluric two-dimensional forward by finite element-radial point interpolation method

LI Jun-jie¹, YAN Jia-bin²

(1. Zhejiang Design Institute of Water Conservancy and Hydroelectric Power, Hangzhou 310002, China;

2. Key Laboratory of Nonferrous Resources and Geological Hazard Detection,

School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)

Abstract: Polynomial basis interpolation method (RPIM), as a kind of typical interpolation meshfree method, was proposed to overcome the defects of point interpolation method (PIM) that the construction process of the shape function involves the matrix inverse operation. This method overcomes the matrix inverse problem, and supports the wider domain dimensionless size interval to better deal with all kinds of engineering and scientific computing problems. The approximate principle of RPIM was introduced in detail, and the discrete system matrix expression corresponding to the magnetotelluric two-dimensional variational problem by combining the Galerkin method and the gauss integral formula was deduced. In order to overcome the defects of low computational efficiency of RPIM, the finite element-radial point interpolation method (FE-RPIM) based on coupling the FEM and RPIM was proposed. The conclusions were verified by the numerical calculation of several models. The results show that RPIM has the advantage of high precision and convenience to calculate complex models, and FE-RPIM has the characteristics of high calculation efficiency for complex models.

Key words: radial point interpolation method; finite element; meshfree method; magnetotelluric

正演计算是研究大地电磁场响应规律的基础,高维问题的大地电磁场响应往往不存在解析解,为此须借助数值计算方法，如：有限差分法(FDM)^[1-2]、积分方程法(IEM)^[3]及有限元法(FEM)^[4-7]。

作为大地电磁正演计算的常用网格方法有着各自的优缺点：FDM实现过程直接，但无法处理复杂地球物理模型；IEM只须对异常体进行剖分和求积，不涉及微分方法中的吸收边界等复杂问题，在三维电磁数值模拟研究中具有快速、方便等特点，但同样无法应对地下电阻率复杂时的计算；有限元法适用于复杂物性分布和复杂边界形状的计算，其最大缺陷在于求解复杂模型时网格生成困难。无单元Galerkin法(EFGM)^[8-9]通过局部支持域内的节点构造形函数及建立离散系统方程，是一种基于节点的无网格数值方法。该方法形函数的构造不涉及网格生成，计算精度高，复杂模型的计算比有限元法便利，广泛应用于有限元法所触及的领域且成功地解决了某些网格方法难以处理的问题^[10-12]。EFGM在地球物理学领域也有少量应用，研究的内容主要集中在地震波场^[13-17]、雷达波场^[18-19]及大地电磁场^[20-22]响应的计算。波场响应的计算证明了EFGM的有效性，但未深入讨论此方法相比于有限元法的优缺点。大地电磁场响应的计算体现了EFGM处理复杂模型较常规网格方法便利的优势。

径向基点插值法(RPIM)^[23]是为改善无网格点插值法(PIM)^[24-25]在节点分布不合理时无法顺利构造形函数的缺陷而提出的，与EFGM的区别主要在于形函数的构造方式。RPIM与PIM形函数采用点插值的方法构造，满足Kronecker delta函数性质，第一类边界条件的加载比形函数采用拟合方法构造的EFGM便利，然而RPIM在地球物理学领域的研究还未见报导。本文作者详细介绍了RPIM形函数的构造过程，从大地电磁二维变分问题出发，采用Galerkin法并结合高斯积分公式推导了相应的系统矩阵离散表达式。由于RPIM计算效率较低^[23]，将其与高效的FEM相耦合，形成了有限元-径向基点插值法(FE-RPIM)，数值计算结果表明FE-RPIM继承了FEM计算效率高及RPIM计算复杂模型便利的优点，是一种优越的计算方法。

1 大地电磁二维变分问题

当地下电性结构为二维时，取z轴垂直向下，x轴指向北，y轴指向东，求解域Ω为矩形区域，4个顶点依次以A、B、C、D顺时针编号，Γ₁为地质体的边界(见图1)。

图1 大地电磁二维正演求解区域

Fig. 1 Solving domain of magnetotelluric two-dimensional forward

当入射电磁波为平面电磁波时，满足式(1)的变分问题^[26]：

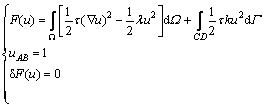(1)

式中：是二维哈密顿算子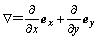，；；取时谐因子为，对于电场极化模式(TE模式)：

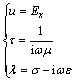(2)

对于磁场极化模式(TM模式)可知：

(3)

式中：ω为角频率；μ为磁导率；σ为电导率；ε为介电常数；E_x与H_x分别为电场与磁场的水平分量。

2 大地电磁二维变分问题的无网格解法

RPIM利用位于积分点支持域内的场节点构造形函数，优点在于引入的径向基函数改善了由多项式基构造形函数所引起的奇异性问题。RPIM形函数满足Kronecker delta函数性质(N_i(X)=δ_ij)，第一类边界条件的加载较便利。图2所示为RPIM中的背景网格、支持域、积分点与场节点示意图，由于背景网格的积分常选用高斯积分法，故积分点又称高斯积分点或高斯点。

图2 RPIM中背景网格、支持域、积分点与场节点示意图

Fig. 2 Schematic diagram of background grid, support domain, gauss points and nodes in RPIM

2.1 支持域

支持域的形状如图2所示，常用的支持域形状有圆形与矩形两种，对于任一高斯点X_Q，支持域尺寸d表达式如式(4)所示：

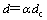(4)

式中：α为支持域的无量纲尺寸，用于控制支持域的大小，是对计算精度影响很大的参数^[8]；d_c为位于高斯点X_Q附近的平均结点间距，表达式如式(5)所示：

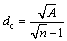(5)

式中：A为预估的支持域面积；n为包含在A中的节点数。对于节点均匀分布的情况，d_c为节点间距。在本研究中，采用矩形支持域，故有两个方向的支持域尺寸，如式(6)所示：

(6)

式中：d_cx与d_cy分别为横向和纵向节点间距；α_x与α_y为横向和纵向的支持域无量纲尺寸。为便于程序设计，常取α_x=α_y=α，在本研究中，取α=1.0。

2.2 径向基点插值近似(RPIM)

求解域Ω中任意一点X处的场变量u(X)的径向基点插值近似表达式为

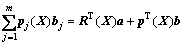(7)

式中：R^T(X)为径向基函数(RBF)；p(X)为二维空间坐标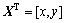的基函数；a与b是系数向量；n为RBF的个数；m为单项式的个数。

常用的RBF有多二次曲面(MQ)函数、薄板样条(TPS)函数、高斯函数及对数函数^[23]。FRANKE^[27]比较了29种离散数据插值的精度，通常情况下MQ函数与TPS函数精度最高^[27]。在本研究中，选择MQ函数,其表达式如下

(8)

式中：d_c为与节点间距有关的特征长度，当节点均匀分布时可取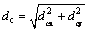；d_cx和d_cy分别d_c在x与y方向的分量；x与y为高斯点位置的坐标，x_i与y_i为支持域内节点的坐标；α_c与q为径向基函数的形状参数,不同学科领域形状参数的最优值一般不同，数值试验研究表明参数q比参数α_c对RPIM性能的影响大，在节点等间距分布情况下，α_c的取值区间约为[-40，40]，q的取值区间约为[-2，0.9]且q≠0，由此可见，基于MQ函数的RPIM在大地电磁正演计算具有很好的普适性，本研究的数值计算中取α_c=1.3，q=0.5。

式(7)中的p(X)可用Pascal三角形确定，对于一维(1D)和二维(2D)空间，其线性基函数分别为

(9)

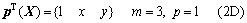(10)

其二次基函数分别为

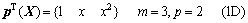(11)

(12)

完备的p阶多项式一般可表示为

(13)

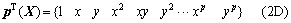(14)

适当增加基函数的阶次能提高无网格法的近似精度，但也降低了计算效率。基函数的形式并不只局限于多项式，也可采用其他不同特性的函数，如楔形函数^[28]、带权的正交函数^[29]、小波基函数^[30]。

将式(7)转化成矩阵的形式如式(15)所示：

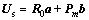(15)

式中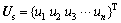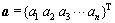：；；。R₀与P_m的展开式分别如式(16)和(17)所示：

(16)

(17)

式(15)中有n+m个变量。m个约束条件如式(18)所示：

(18)

结合式(9)与(12)可得到矩阵方程如式(19)所示：

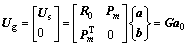(19)

式中：；。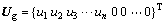

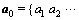
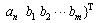因为矩阵R₀是对称的，故矩阵G也是对称的，求解式(19)可得式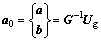(20)：

(20)

将式(15)写为矩阵的形式有

(21)

将式(20)代入式(21)得

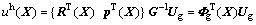(22)

式中：，取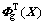的前n项计算点X在支持域内的LRPIM形函数，其表达式为

(23)

相应的导数表达式为

(24)

RPIM改善了PIM插值函数的奇异性问题^[23]，RPIM形函数满足Kronecker delta函数性质，第一类边界条件加载便利。然而径向基函数中包含了对RPIM计算精度有直接影响的形状参数，形状参数的最优值往往需要通过数值试验获得。

2.3 RPIM离散系统方程的构造

方程式(1)取变分有

(25)

(26)

式中：Φ为形函数矩阵；n为支持域内的节点数；u为支持域内n个节点的场向量。对式(26)进行变分运算有

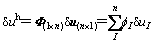(27)

将式(26)与(27)代入式(25)，结合变分问题采用的坐标系统，得到方程式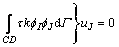(28)：

(28)

式(28)采用支持域内n个场节点编号，对于求解域内所有场节点还应有一个用于将局部节点矩阵组装成总体刚度矩阵的总体编号体系。当节点I和节点J位于不同支持域时，其相应的被积函数为0，因此可得到按求解域节点编号的总体编号体系方程如式(29)所示

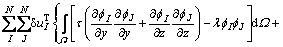
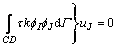(29)

式中：N为场节点总数。

式(29)可简写为

(30)

由于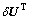是任意的，故式(30)成立的条件为

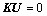(31)

式(31)即为RPIM构造的系统方程。K的表达式中包含对求解域Ω与求解域边界Γ的积分。计算这些积分，需将求解域离散成一组背景网格(见图2)，总体积分可表示成这些单元积分之和的形式，每个单元的积分利用高斯积分法求解，有

(32)

式中：n_c与n_c_Γ分别为背景单元及边界单元的个数；n_g与n_g_Γ分别为背景单元及边界单元内的高斯点数目；ω_i为第i个高斯点X_Qi的权系数；与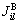分别为背景单元k在积分点X_Qi处面积分及子边界l在积分点X_Qi处曲线积分的雅可比矩阵。式(32)即为总体刚度矩阵的离散表达式，为带状、对称的稀疏矩阵^[23]。

2.4 FE-RPIM离散系统方程的构造

RPIM计算效率低但能方便地处理复杂模型，FEM计算高效，因此将两者耦合起来。RPIM与FEM系统矩阵都是由(4×4)阶小矩阵块状累加至总体矩阵中形成的，这构成了RPIM与FEM耦合的基础。

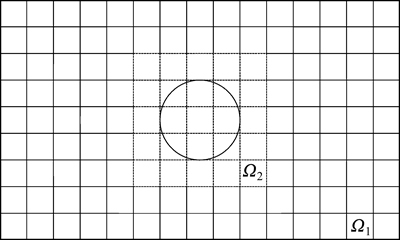
图3 FE-RPIM中计算模型2的有限单元与背景网格分布示意图

Fig. 3 Schematic diagram of finite element and background grid distribution for numerical calculation of model 2 in FE-RPIM

如图3所示，FE-RPIM的基本思想是将求解区域Ω划分为实线的有限单元的FEM区域Ω₁及虚线的背景单元RPIM区域Ω₂，为了利用FEM计算高效及RPIM计算复杂模型便利的优点，FEM区域面积往往占多数，且异常体一般置于RPIM区域中。对式(1)取变分并将FEM区域单元离散化可得

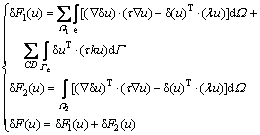(33)

先将FEM区域的积分项即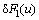离散如式(34)所示：

(34)

式中：a与b分别为单元的横纵向宽度；K_1e、K_2e、K_3e均为4×4阶矩阵，将它们扩展成全体节点的矩阵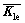、、可得

(35)

对离散，与式(35)的区别仅在于无网格节点数目的不同，参照式(30)得

(36)

式中：M₁与M_n表示RPIM区域第一个节点与最后一个节点的编号，同样K^RPIM中包含的积分可用式(32)的高斯积分法求解。背景网格积分是RPIM中最重要的数值计算问题之一，总积分点数一般取支持域内场节点的数量的2~8倍，但高斯点数目的增加并不能显著提高无网格法的计算精度反而极大地降低了计算效率^[22]，因此，每个背景单元仅采用4(2×2)个高斯点，每个边界单元采用2个高斯点。将式(35)与(36)相加得

(37)

由于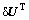是任意的，故式(37)成立的条件为

(38)

式(38)即为FE-RPIM构造的系统方程，由于FEM与RPIM构造总体矩阵K^FEM与K^RPIM均为带状、对称、

稀疏的，因此FE-RPIM构造的总体矩阵K也具有带状、对称、稀疏的性质。

求解线性方程组KU=0还需加载边界条件，在本研究中，采用简单易行的罚函数法，将刚度矩阵中相应的对角元素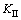变为，α为惩罚系数，其值可取1×10⁴~1×10¹⁰，然后将边界上的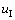值取代方程组右端的零向量即可。

3 正演计算

3.1 三层模型

首先通过三层模型来观察数值算法(FEM、RPIM、PIM)的计算精度。第一层电阻率ρ₁=500 Ω·m，层厚h₁=1 km；第二层电阻率ρ₂=2000 Ω·m, 层厚h₂=3 km；第三层电阻率ρ₃=100 Ω·m 。场节点等间距分布于求解域，对于TE模式，使用3321(41×81)个场节点和3200(40×80)个背影网格，横纵向节点间距均为200 m。对于TM模式，使用1681(41×41)个场节点和1600(40×40)个背影网格，节点间距与TE模式相同。有限元法节点的分布与无网格法一致。

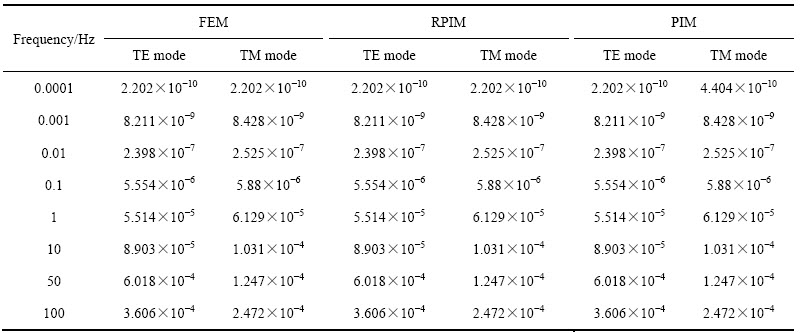
表1和2所列分别为三层模型视电阻率和阻抗相位数值计算的相对误差，相对误差值的大小对应着数值方法计算精度的高低，相对误差值越大，精度越低，反之则精度越高。由表1可知，3种数值算法(FEM、RPIM与PIM)计算精度均很高且量级相同，都随频率的增高而降低，精度变化范围约为3×10^-10~4×10^-3；阻抗相位数值计算精度变化规律与视电阻率类似，精度约为2×10^-10~4×10^-4(见表2)。

表1 三层模型视电阻率数值解的相对误差

Table 1 Numerical solutions relative error of apparent resistivity for three-layer model

表2 三层模型阻抗相位数值解的相对误差

Table 2 Numerical solutions relative error of impedance phase for three-layer model

3.2 方形截面二度体模型

验证RPIM求解MT问题的有效性，采用与三层模型相同的节点分布计算了方形截面二度体模型(见图4)：异常体边长L=400 m，电阻率ρ₂=100 Ω·m，埋深h=800 m，求解域背景电阻率ρ₁=1000 Ω·m，工作频率f=1×10^-⁴~1×10³ Hz。

图4 方形截面二度体模型

Fig. 4 Two-dimensional model of square cross-section

数值计算结果显示RPIM、FE-RPIM和FEM计算的视电阻率断面图完全一致。图5(a)所示为RPIM的TE模式视电阻率断面图，低阻异常呈椭圆状，低阻异常横向上比实际低阻体范围大，视电阻率变化范围为780~1050 Ω·m；TM模式视电阻率断面图中，低阻异常呈直立无限向下延伸，低阻体横向位置与实际低阻体一致，但低阻异常无下边界，视电阻率ρ变化范围为840~1060 Ω·m，较好地反映出了异常体的存在。图5(b)所示为FEM数值计算结果，对比图5(a)可知， RPIM与FEM断面图仅在TE模式下有细微差别，TE模式FEM断面图视电阻率变化范围为770~1050 Ω·m，验证了RPIM二维算法的正确性。

3.3 圆形截面二度体模型

RPIM是为克服FEM网格生成困难的缺陷而提出的，是一种节点方法，模型参数加载于只与坐标有关的高斯点上，一个背景网格内的几个高斯点可以有各自不同的物性参数值，因此，处理复杂模型较常规网格方法便利，FE-RPIM作为FEM与RPIM的耦合同样继承了这一特性，为体现RPIM及FE-RPIM这一优势，采用与方形截面二度体模型相同的节点分布计算了圆形截面二度体模型(见图6)，截面半径R=200 m，其余参数与方形截面二度体相同。

图7所示为圆形截面二度体模型RPIM与FE-RPIM视电阻率计算结果，两种方法计算结果断面图相同。对比方形截面二度体模型(见图5)可以看出,两者形态基本相似，图7中视电阻率幅值与异常幅值的变化范围略小，这与圆形截面低阻体规模比方形截面二度体略小一致。

3.4 脉状体模型

为了验证RPIM与FE-RPIM处理复杂地质体边界的能力，计算了两个不同倾角的脉状体模型(见图8)：截面下底面a=400 m，上下底面间距h=600 m，异常体右边界与地面的夹角分别呈45°与30°，电阻率、围岩电阻率及前点分布情况与上述的二维模型相同，工作频率f为16~2048 Hz。

图5 方形截面二度体模型RPIM、FEM的视电阻率断面图

Fig. 5 Numerical solutions of apparent resistivity by RPIM and FEM for model of square cross-section

图6 圆形截面二度体模型

Fig. 6 Two-dimensional model of circular cross-section

图9所示为脉状体模型TE模式RPIM与FE-RPIM计算结果。由图9可见，脉状体的视电阻率断面左右不对称，低阻区域呈“上窄下宽”倾斜条带状分布，倾向与地质体的倾向相同。45°脉状体视电阻率变化范围为100~1100 Ω·m。30°脉状体视电阻率变化范围为50~1200 Ω·m，较45°脉状体低阻条带呈现更小的倾角。

3.5 数值算法效率

虽然RPIM计算效果良好，却是一种低效率的数值方法，FE-RPIM提高了计算效率。表3所列为17个计算频点下方形截面二度体模型的RPIM、FE-RPIM及FEM计算耗时t。由表3可知，RPIM计算耗时约为FEM的9倍，FE-RPIM的耗时相比于RPIM更少，且随着RPIM区域的减少，计算耗时显著降低，采用背景网格(10×4)的FE-RPIM计算效率已和FEM的相当。

4 结论

1) 将RPIM及FE-RPIM应用于大地电磁二维正演，采用径向基点插值原理构造了RPIM形函数；从大地电磁二维变分问题出发采用Galerkin法并结合高斯积分公式推导了RPIM及FE-RPIM的总体矩阵离散表达式，通过试验分析得出了大地电磁二维正演问题的径向基函数形状参数建议值：α_c=1.3，q=0.5。

图7 圆形截面二度体模型RPIM与FE-RPIM视电阻率断面图

Fig. 7 Numerical solutions of apparent resistivity by RPIM and FE-RPIM for model of circular cross-section

图8 脉状二度体模型

Fig. 8 Two-dimensional vein-like models

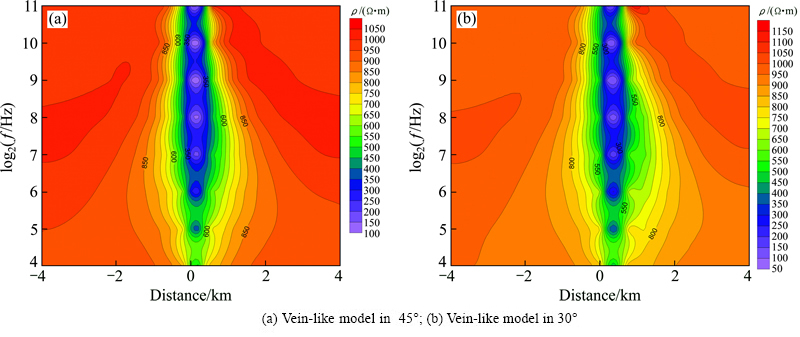
图9 TE模式脉状体模型RPIM与FE-RPIM视电阻率断面图

Fig. 9 Numerical solutions of apparent resistivity for vein-like model by RPIM and FE-RPIM in TE mode

表3 方形截面模型数值方法计算耗时

Table 3 Computation time of numerical methods for model of square cross-section

2) 采用节点均匀分布的FEM、RPIM及PIM计算了三层模型的大地电磁场响应，计算结果表明3种数值方法计算精度相当，固定网格下精度随频率的增高而降低。在10^-⁴~10² Hz频段，视电阻率精度变化范围约为3×10^-10~4×10^-3，视相位精度约为2×10^-10~4×10^-4。

3) 用RPIM与FEM计算了方形截面二度异常体的大地电磁场响应，两者断面图形态基本一致，进一步验证了RPIM算法的有效性；柱形二度体及倾斜条带状二度体大地电磁场响应体现了RPIM在处理复杂模型问题较常规网格方法便利的优势。

4) 结合RPIM处理复杂模型便利及FEM计算高效的特性，将两种方法耦合形成了FE-RPIM。方形截面二度异常体FE-RPIM计算结果与FEM一致，验证了耦合算法的正确性以及构建地质模型的优越性。

5) 对比了RPIM、FE-RPIM及FEM的计算效率，RPIM计算耗时约为FEM的9倍。FE-RPIM计算时异常体所在的区域往往较小(占求解域的1/40)，故计算耗时低于RPIM的而略高于FEM的。随着FEM区域的增大，FE-RPIM耗时将逐渐趋于FEM的。本研究中无网格区域(10×4)的FE-RPIM耗时与RPIM耗时相比，在TE模式下效率提高约87%，在TM模式下效率提高约84%。因此，FE-RPIM综合了RPIM处理复杂模型便利及FEM计算高效的优点，是一种优越的数值方法。

REFERENCES

[1] 陈辉, 邓居智, 谭捍东, 杨海燕. 大地电磁三维交错网格有限差分数值模拟中的散度校正方法研究[J]. 地球物理学报, 2011, 54(6): 1649-1659.

CHEN Hui, DENG Ju-zhi, TAN Han-dong, YANG Hai-yan. Study on divergence correction method in three-dimensional magnetotelluric modeling with staggered-grid finite difference method[J]. Chinese Journal of Geophysics, 2011, 54(6): 1649-1659.

[2] 董浩, 魏文博, 叶高峰, 金胜, 景建恩. 基于有限差分正演的带地形三维大地电磁反演方法[J]. 地球物理学报, 2014, 57(3): 939-952.

DONG Hao, WEI Wen-bo, YE Gao-feng, JIN Sheng, JING Jian-en. Study of Three-dimensional magnetotelluric inversion including surface topography based on finite-difference method[J]. Chinese Journal of Geophysics, 2014, 57(3): 939-952.

[3] WANNAMAKER P E. Advances in three-dimensional magnetotelluric modeling using integral equations[J]. Geophysics, 1991, 56(11): 1716-1728.

[4] 刘云, 王绪本. 电性参数分块连续变化二维MT有限元数值模拟[J]. 地球物理学报, 2012, 55(6): 2079-2086.

LIU Yun, WANG Xu-ben. The FEM for modeling 2-D MT with continuous variation of electric parameters within each block[J]. Chinese Journal of Geophysics, 2012, 55(6): 2079-2086.

[5] KEY K, WEISS C. Adaptive finite-element modeling using unstructured grids: The 2D magnetotelluric example[J]. Geophysics, 2006, 71(6): 291-299.

[6] 刘长生, 汤井田, 任政勇, 冯德山. 基于非结构化网格的三维大地电磁自适应矢量有限元模拟[J]. 中南大学学报(自然科学版), 2010, 41(5): 1855-1859.

LIU Chang-sheng, TANG Jing-tian, REN Zheng-yong, FENG De-shan. Three-dimension magnetotellurics modeling by adaptive edge finite-element using unstructured meshes[J]. Journal of Central South University (Science and Technology), 2010, 41(5): 1855-1859.

[7] REN Zheng-yong, TANG Jing-tian. 3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method[J]. Geophysics, 2010, 75(1): 7-17.

[8] BELYTSCHKO T, LU Y Y, GU L. Element-free Galerkin methods[J]. International Journal for Numerical Methods in Engineering, 1994, 37(2): 229-256.

[9] DOLBOW J, BELYTSCHKO T. An introduction to programming the meshless element free Galerkin method[J]. Archives of Computational Methods in Engineering, 1998, 5 (3): 207-241.

[10] BELYTSCHKO T, LU Y Y, GU L. Fracture and crack growth by element-free Galerkin methods[J]. Modelling and Simulation in Materials Science and Engineering, 1994, 2(3): 519-534.

[11] LI Dong-ming, BAI Fu-nong, CHENG Yu-min, LIEW K M. A novel complex variable element-free Galerkin method for two-dimensional large deformation problems[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 233/236(1): 1-10.

[12] LIU Lei-chao, DONG Xiang-huai, LI Cong-xin. Adaptive finite element-element-free Galerkin coupling method for bulk metal forming processes[J]. Journal of Zhejiang University-Science A, 2009, 10(3): 353-360.

[13] 贾晓峰, 胡天跃. 滑动最小二乘法求解地震波波动方程[J]. 地球物理学进展, 2005, 20(4): 920-924.

JIA Xiao-feng, HU Tian-yue. Solving seismic wave equation by moving least squares (MLS) method[J]. Progress in Geophysics, 2005, 20(4): 920-924.

[14] 贾晓峰. 复杂介质中地震波模拟与成像的无单元数值算法[D]. 北京: 北京大学, 2005.

JIA Xiao-feng. Element-free Galerkin method for seismic numerical modeling and imaging in complex media[D]. Beijing: Peking University, 2005.

[15] 贾晓峰, 胡天跃, 王润秋. 复杂介质中地震波模拟的无单元法[J]. 石油地球物理勘探, 2006, 41(1): 43-48.

JIA Xiao-feng, HU Tian-yue, WANG Run-qiu. A mesh-free algorithm of seismic wave simulation in complex medium[J]. Oil Geophysical Prospecting, 2006, 41(1): 43-48.

[16] 贾晓峰, 胡天跃, 王润秋. 无单元法用于地震波波动方程模拟与成像[J]. 地球物理学进展, 2006, 21(1): 11-17.

JIA Xiao-feng, HU Tian-yue, WANG Run-qiu. Wave equation modeling and imaging by using element-free method[J]. Progress in Geophysics, 2006, 21(1): 11-17.

[17] 王月英. 地震波正演模拟中无单元Galerkin法初探[J]. 地球物理学进展, 2007, 22(5): 1539-1544.

WANG Yue-ying. Study of element-free Galerkin method in the seismic forward modeling[J]. Progress in Geophysics, 2007, 22(5): 1539-1544.

[18] 冯德山, 王洪华, 戴前伟. 基于无单元Galerkin法探地雷达正演模拟[J]. 地球物理学报, 2013, 56(1): 298-308.

FENG De-shan, WANG Hong-hua, DAI Qian-wei. Forward simulation of ground penetrating radar based on the element-free Galerkin method[J]. Chinese Journal of Geophysics, 2013, 56(1): 298-308.

[19] 戴前伟, 王洪华. 基于随机介质模型的GPR无单元法正演模拟[J]. 中国有色金属学报, 2013, 23(9): 2436-2443.

DAI Qian-wei, WANG Hong-hua. Element free method forward modeling of GPR based on random medium model[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(9): 2436-2443.

[20] 苏洲, 胡文宝, 朱毅. 二维大地电磁正演中无网格算法研究[J]. 石油天然气学报, 2012, 34(5): 87-90.

SU Zhou, HU Wen-bao, ZHU Yi. Meshfree method used in two-dimensional magnetotelluric forwarding[J]. Journal of Oil and Gas Technology, 2012, 34(5): 87-90.

[21] 李俊杰, 严家斌. 无网格法进展及其在地球物理学中的应用[J]. 地球物理学进展, 2014, 29(1): 452-461.

LI Jun-jie, YAN Jia-bin. Developments of meshless method and applications in geophysics[J]. Progress in Geophysics, 2014, 29(1): 452-461.

[22] 严家斌, 李俊杰. 无网格法在大地电磁正演计算中的应用[J]. 中南大学学报(自然科学版), 2014, 45(10): 3513-3520.

YAN Jia-bin, LI Jun-jie. Magnetotelluric forward calculation by meshless method[J]. Journal of Central South University (Science and Technology), 2014, 45(10): 3513-3520.

[23] WANG J G, LIU G R. A point interpolation meshless method based on radial basis functions[J]．International Journal for Numerical Methods in Engineering, 2002, 54(11): 1623-1648.

[24] LIU G R, GU Y T. A point interpolation method for two-dimensional solids[J]. International Journal for Numerical Methods in Engineering, 2001, 50(4): 937-951.

[25] 李俊杰, 严家斌. 无网格点插值法大地电磁二维正演数值模拟[J]. 石油物探, 2014, 53(5): 617-626.

LI Jun-jie, YAN Jia-bin. Magnetotelluric two-dimensional forward numerical modeling by meshfree point interpolation method[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 617-626.

[26] 徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994: 229-235.

XU Shi-zhe. Finite element method for geophysics[M]. Beijing: Science Press, 1994: 229-235.

[27] FRANK R. Scattered data interpolation: Tests of some methods[J]. Mathematics of Computation, 1972, 38(157): 181-199.

[28] 署恒木, 黄朝琴, 李翠伟. 基于楔形基函数的一种新型无网格法[J]. 中国石油大学学报(自然科学版), 2008, 32(3): 108-113.

SHU Heng-mu, HUANG Zhao-qin, LI Cui-wei. A novel meshless method based on ridge basis function[J]. Journal of China University of Petroleum (Edition of Natural Science), 2008, 32(3): 108-113.

[29] 赵云亮. 无网格法基函数的改进与应用[D]. 长春: 吉林大学, 2008.

ZHAO Yun-liang. Improvement and application of the basis of element-free method[D]. Changchun: Jilin University, 2008.

[30] 吴琛, 周瑞忠. 小波基无单元法及其与有限元法的比较[J]. 工程力学, 2006, 23(4): 28-32.

WU Chen, ZHOU Rui-zhong. Element free galerkin method with wavelet basis and its comparison with finite element method[J]. Engineering Mechanics, 2006, 23(4): 28-32.

(编辑王超)

基金项目：国家自然科学基金资助项目(40874055)；湖南省自然科学基金资助项目(07JJ5065)

收稿日期：2014-08-11；修订日期：2015-01-14

通信作者：严家斌，副教授，博士；电话：13548942513；E-mail：cspyry@csu.edu.cn

摘要：径向基点插值法(RPIM)作为一种插值型无网格方法，为改善无网格点插值法(PIM)在形函数构造过程中可能出现的矩阵奇异性问题而提出的一种方法，该算法支持域无量纲尺寸的选择区间大，能更好地处理各类工程与科学计算问题。介绍了RPIM的近似原理，给出了径向基函数形状参数的推荐值；从大地电磁二维变分问题出发利用Galerkin法结合高斯积分公式推导出相应的系统矩阵离散表达式；为提高RPIM的计算效率，将RPIM与有限元法(FEM)耦合，提出了有限元－径向基点插值法(FE-RPIM)，多个模型的数值计算验证了RPIM精度高、处理复杂模型便利及耦合法计算复杂模型高效的特点。