Trans. Nonferrous Met. Soc. China 29(2019) 1721-1727

Enhanced Cu/graphene adhesion by doping with Cr and Ti: A first principles prediction

Yang LIU^1,2, Gang WANG¹, Yi-ren WANG¹, Yong JIANG^1,3, Dan-qing YI¹

1. Key Laboratory of Nonferrous Metal Materials Science and Engineering, Ministry of Education, School of Materials Science and Engineering, Central South University, Changsha 410083, China;

2. School of Materials Science and Engineering, University of Pennsylvania, Philadelphia 19104, USA;

3. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China

Received 19 November 2018; accepted 14 March 2019

Abstract:

We presented a density functional theory study on doping effects of transition metals (Cr and Ti) on the Cu/graphene interface adhesion. Various undoped Cu/graphene interface structures were constructed using both the sandwich and the surface models. Energetics calculations showed that the interface binding strength only weakly depends on interface coordination. Both interface models predicted the top-fcc coordination type as the most energy-favored, with a low binding energy value. Segregated Cr prefers to substituting for Cu, while Ti occupies a hollow site at the interface. Although the segregation tendencies are both very weak, once present on the interface, both dopants can greatly increase the interface binding energy and improve the adhesion.

Key words:

Cu; Cr; Ti; grapheme; doping; interface; first principles;

1 Introduction

Graphene is essentially a unique, two-dimensional hexagonal lattice of carbon atoms and possesses many extraordinary electronic, mechanical, and thermal properties [1]. Using the chemical vapor deposition (CVD) technique, large-size high-quality graphene can be practically synthesized through direct atomic deposition of carbon on transition- or noble-metal substrates followed by a chemical transfer process [2-8]. Such a fabrication technique makes graphene economically viable for many promising applications, such as nano-electronics and composite structural materials [9-11]. However, the properties of as-produced graphene and graphene-based devices are very sensitive to CVD processing parameters, and especially to the substrate conditions. Previous studies have suggested that interaction between the graphene single layer and the metal surface may play very important role in tuning the integration and properties of the devices [12-14]. It is worthwhile clarifying the nature of graphene/metal interfaces and the potential role on the overall performance of the devices and materials. Exploring new, future applications of graphene has also consistently stimulated the research on graphene/metal interfaces.

Generally, the interaction between graphene and metal substrates can be classified into two categories [15]: strong binding with metals (such as Co, Ni, and Pd), and weak binding with metals (such as Ag, Au, Cu, Pt, and Al). Clarification of the composition, structure, and property relation of these metal/graphene interfaces is highly demanded for developing new graphene-based devices and graphene-reinforced metallic composites. Although many research efforts have been devoted, it is still too challenging for experimentalists to directly characterize the interface structures and properties of graphene, especially when it is deeply embedded inside a metal matrix, as often seen in graphene-reinforced metallic composites.

First-principles calculations have been often resorted to meet this gap. Using a surface model for the interface, XU and BUEHLER[16] considered different orientations of graphene on top of the Cu(111) and Ni(111) facets with three typical coordination types (top-fcc, top-hcp, and hcp-fcc), and predicted the top-fcc as the most energy-favored. FUENTES-CABRERA et al [17] further suggested that the bridge coordination has a similarly low energy and thus might also present on the graphene/Ni(111) interface. KHOMYAKOV et al [18] attributed the graphene’s band-gap opening to its interaction with the metal surfaces (Co, Ni, and Pd), due to the hybridization between grapheme p_z states and metal d states. However, all these first-principles calculations were performed using the surface model for the interface, that is, the single layer graphene on top of one selected metal facet. To our best knowledge, no first-principles studies have been performed on one single layer graphene embedded inside a metal matrix, which, however, will be much realistic for graphene- reinforced metallic composites.

It was predicted that the Cu/graphene interface can be only weakly bonded [15]. One may thus infer that a Cu/graphene-based nano electronic device or a graphene-reinforced copper composite can hardly be robust. However, copper is an excellent electrical and heat-conducting constituent, and is widely employed in many electrical/electronic and heat-exchange devices. Finding a solution to improve the Cu/graphene interface adhesion is always attractive and worth exploring. Some transition metals, such as Cr and Ti, have shown a strong tendency to form carbides in nature [19,20]. Recent experiments [21,22] also suggested that doping Cr into a copper/diamond system improved its mechanical properties, although the responsible mechanism has been yet to be clarified. Inspired by these facts, we carried out first principles density functional theory calculations in this study to evaluate the potential effects of doping Cr and Ti on the embedded graphene/Cu interface, using the sandwich model for the interface. Based on our results, some doping strategies for improving the interface adhesion were suggested.

2 Computational details

The embedded single layer graphene in Cu was modeled using a sandwich supercell of Cu/graphene/Cu, and the results were compared with those of the surface-model calculations. Previous surface-model calculations on the grapheme/metal interfaces [16,17,23] revealed that the exchange-correlation (XC) functionals of Perdew-Burke-Ernzerhof (PBE) [24] always underestimated the interface binding energy. A PBE- based calculation even predicted the debonding of the grapheme/Ni(111) interface [17]. In the present study, we employed local density approximation (LDA) [25] for exchange-correlation functional as implemented in the plane-wave density functional theory code: VASP [26]. For a better accuracy, the projector- augmented wave (PAW) [27] potentials were chosen for all involved species, i.e. C, Cu, Cr, and Ti. Within the LDA scheme, the bond length of Cu was predicted as 2.49 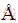, and the first-nearest neighboring C—C bond length of graphene as 1.41 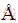. Both favorably agree with experiments (2.55 [28] and 1.42 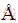[29], respectively). As the most stable facet, the Cu(111) was chosen as the substrate surface. In the Cu(111)/graphene/Cu(111) sandwich supercell, each Cu(111) block consists of five atomic layers, separating by a vacuum thickness of over 12 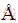to avoid any possible image interaction. The van der Walls interactions between the interlayers were neglected since only single layer of graphene was considered in the model. A 9×9×1 Monkhorst-Pack k-mesh [30] was employed for sampling the Brillouin zone. All structures were optimized under a high energy cutoff of 800 eV for plane-wave basis sets until the atomic force was converged to less than 0.02 eV/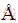. With all these settings, the following calculations were performed.

(1) The interface binding energy, ΔE_B, with various possible coordination types being considered (top-fcc, top-hcp, hcp-fcc, bridge-top, bridge-fcc, and bridge-hcp). The values were compared to determine the most energy- favored structure. Meanwhile, the surface-model approach was also adopted for interface binding energy calculations, in order to offer a comparison between the two models.

(2) The segregation energy, ΔE_seg, of Cr or Ti, from the unstrained Cu bulk interior to various interfacial sites. A segregation process is energetically permitted only when the process is exothermic.

(3) The work of separation, W_sep, for both the clean and segregated interface, as the cleavage energy required to split the interface apart rigidly. The work of separation measures the brittle fracture strength of the interface.

3 Results and discussion

3.1 Interface structures

All previous calculations on the graphene/Cu interface employed the surface model by placing the single layer graphene directly on the top of a metal surface. The only exception is the work of ADAMSKA et al [31], where they added one atomic layer of Cu or Ni on the top of the graphene/Cu(111) or the graphene/Ni(111). In the real-world scenarios of composite structural materials, graphene is deeply embedded inside the metal matrix. It is thus important to first assess the two interface models, i.e. the surface and the sandwich models.

Given the metal surface facet and the associated interface strain, the atomic structure of graphene/metal interface would be solely determined by interfacial coordination. Interfacial coordination describes the relative positions of atoms on graphene with respect to the metal surface atoms. Following the nomenclature in

Refs. [16,18], a total of six typical coordination types can be constructed in Fig. 1, i.e. top-hcp, top-fcc, hcp-fcc, bridge-top, bridge-hcp, and bridge-fcc. Here, the top, hcp, or fcc represents the A, B, or C layer of Cu(111) in its fcc stacking sequence, respectively. The top-hcp, top-fcc, or hcp-fcc defines how the two neighboring carbon atoms on the graphene sheet are aligned to the two different Cu(111) layers, while the bridge-top, bridge-hcp, or bridge-fcc defines how the center of the C—C bond on the graphene is aligned to one of the Cu(111) layers with stacking mode A, B, or C, respectively. The resulting interface mismatch with the graphene lattice is minimal, only 1.6%. Full relaxation calculations were performed on these coordinated interface structures. Table 1 summarizes the calculated binding energy ΔE_B (meV/C-atom) and interface separation d₀ (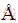), in comparison with our surface-model calculations using LDA functionals. The results in Ref. [31] using the surface model for the interface with PBE functionals are also provided.

Binding energy ΔE_B defined similarly to cohesive energy from Ref. [32] was evaluated by

                    (1)

where E_intf is the total energy of the interface ensemble, E_gr and E_Cu(111) are the total energies of the graphene and the Cu(111) layers calculated using the same size supercell, respectively, and N represents a total number of carbon atoms in the supercell. A negative value of ΔE_B predicts an energy-favored interface structure.

It is suggested from Table 1 that the interface binding energy has only a weak dependence on coordination types, no matter the interface model or the XC functionals used. Nevertheless, the top-fcc coordinated interface has the highest binding strength and is slightly more stable than all the others, being consistent with the finding of THOMAS and LUC [33] using the surface model and the PBE functionals. Calculations also show that the top-fcc interface has the smallest value of interface separation d₀, independent of interface model and XC functionals, and that shorter interface separations always correspond to stronger interfacial binding. It can be regarded as a rule of thumb that the value of interface separation d₀ reflects the binding strength of the graphene/Cu interface.

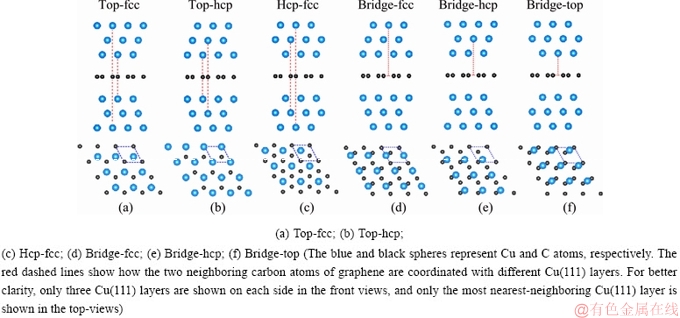
Fig. 1 Sandwich models for Cu(111)/graphene interfaces with different coordination types (Color online)

Table 1 Calculated binding energy ΔE_B and interface separation d₀ for various undoped Cu(111)/graphene interfaces

Please also note that among the three bridge- coordinated configurations, our LDA calculations predicted the bridge-top to be the most stable, no  matter the interface model used. The previous PBE calculations [31]; however, suggested the bridge-fcc to be the most energy-favored one. Obviously, this discrepancy will not be attributed to the interface model, but to the XC functionals used. For all the subsequent calculations, the most energy-favored top-fcc interface was adopted.

3.2 Interface segregation

Table 1 suggests that the embedded graphene sheet can be only weakly bound with the copper matrix. Improving the graphene/metal adhesion is definitely demanded for designing reliable graphene-reinforced composites. To meet this goal, experimental efforts have been consistently made by introducing transition-metal elements as dopants. For instance, Cr was introduced into the Cu/graphite and Cu/diamond composites in order to improve the overall properties of the materials [21,22]. Inspired by these studies, we assessed the potential effects of doping Cr and Ti on the Cu/graphene adhesion.

The interface adhesion is often evaluated in term of the work of separation, W_sep, which can be significantly affected by segregated dopants. To measure the segregation tendency of Cr or Ti from Cu bulk interior to the interface, we first evaluated the preferred sites of the dopants in the Cu bulk by calculating the corresponding formation energies. The substitutional site was found to be the most stable site in Cu for both dopants. For    one dopant atom reaching a substitutional site at the

interface, the segregation energy can be predicted as

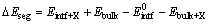            (2)

where 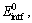E_bulk, E_intf+X, and E_bulk+X are the total energies of the clean interface supercell, the pure Cu bulk supercell, the segregated interface supercell containing  a substitutional X (X=Cr or Ti), and the Cu bulk supercell containing a substitutional X (X=Cr or Ti), respectively. For one dopant atom reaching an interstitial site at the interface, the segregation energy can be predicted as

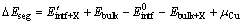       (3)

where is the total energy of the segregated interface supercell, and μ_Cu is the chemical potential of Cu in its pure bulk. A negative value of segregation energy corresponds to an exothermic segregation process that can be thermodynamically permitted. A total of six atomic sites at the Cu/graphene interface can be proposed for the segregated Cr/Ti, including five interstitial sites (i.e. bridge-1, bridge-2, hollow, top-1, and top-2) and one substitutional site, as schematically shown in Fig. 2. The corresponding segregation energies are calculated and compared in Table 2.

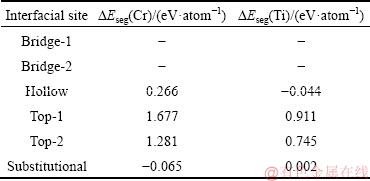
It should be noted that for Cr and Ti, the bridge-1 and bridge-2 configurations will relax self-consistently to the hollow one during calculations, and therefore the corresponding DE_seg values are not provided in Table 2. According to Table 2, Cr and Ti have a very weak tendency to segregate to the Cu/graphene interface (ΔE_seg=-0.065 eV/atom for Cr and -0.044 eV/atom for Ti), but once segregated, Cr prefers the substitutional site while Ti prefers the hollow site at the interface.

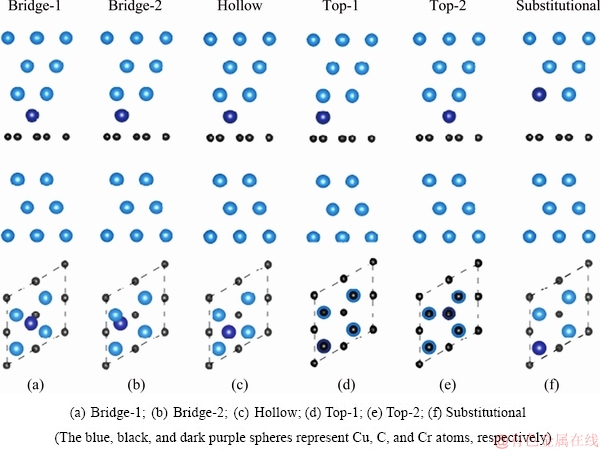
Fig. 2 Six proposed sites for segregated Cr or Ti at Cu/graphene interface (Color online)

Table 2 Calculated segregation energy of Cr or Ti for various interfacial sites

3.3 Interface adhesion

The above calculations have predicted the very weak segregation tendency of Cr and Ti in Cu.  Therefore, one can hardly expect a high coverage of Cr or Ti at the Cu/graphene interface inside a Cu matrix. This implies that conventional doping of Cr or Ti might has only a trivial impact on interface adhesion. But nevertheless, there could exist new techniques that allow a direct doping of extrinsic elements into the interface region. The adhesion of a Cr- or Ti-doped Cu/graphene interface is therefore worthy of study.

The work of separation, W_sep, was then calculated to evaluate the adhesion strength of the Cr/Ti-doped interface. It should be noted that only one side doping was considered in this work due to the weak segregation tendency as we predicted. To separate the interface into two parts I and II, the associated W_sep can be predicted as

W_sep=(E_I+E_II-E_intf+X)/(2A)                       (4)

where E_I and E_II are the total energies of the separated parts I and II, respectively, and A is the interface area in the interface supercell.

Several possible separating positions were considered for the interface as indicated with the dashed lines in Fig. 3. Obviously, the clean interface has a fairly weak adhesion, with W_sep=0.258 J/m² only, in accordance with its low binding energy (DE_B=45 meV/C-atom in Table 1). This level of adhesion strength is even lower than the S-contaminated Cu/Al₂O₃ [34] and Ni/Al₂O₃ [35] interface. However, the adhesion can be greatly enhanced via doping with Cr or Ti. By substituting Cu atoms on the interface, Cr incurs nearly a six-fold increase on W_sep, from 0.258 to 1.483 J/m². The adhesion on the other side of the interface is doubled, up to  0.652 J/m². Ti prefers the hollow sites on the interface. An even stronger adhesion is predicted on the Ti-doped side, with W_sep=2.103 J/m², while on the undoped side, the adhesion is almost unchanged, with a low W_sep of 0.284 J/m².

Figure 4 plots the charge transfer between graphene and doped atoms. Charge accumulation is evident mostly within the vicinity of the Cr atom. The p-ring in graphene is broken, and the accumulated charge spills into the 2p_z-like orbital of C, which is a positive sign of strong chemical interaction between Cr and the underneath C atom. The C—C bond in graphene becomes weak, corresponding to the small charge depletion on the graphene sheet. On the other side of the interface, a small portion of charge accumulation is also found between the C and the underneath Cu atoms, being responsible for the doubled adhesion of W_sep=0.652 J/m². The situation on the Ti-doped interface is different. The Ti atom is sited at a hollow site above the center of the six-C ring, and strongly interacts with the nonlocal p-orbital of graphene by gaining charges from neighboring Cu atoms and perhaps neighboring C atoms too. This interaction is even much stronger, in accordance to almost a ten-fold increase in interlayer adhesion (W_sep=2.909 and 2.103 J/m²). On the other side of the interface, the Cu atoms are nearly intact, remaining a weak binding with the graphene.

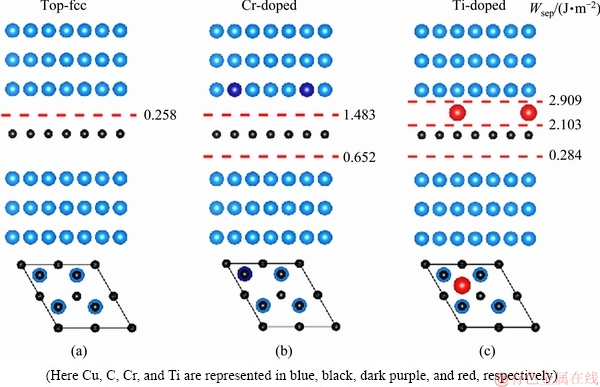
Fig. 3 Calculated work of separation, W_sep, for clean interface (a), Cr-doped interface (b), and Ti-doped interface (c) (Color online)

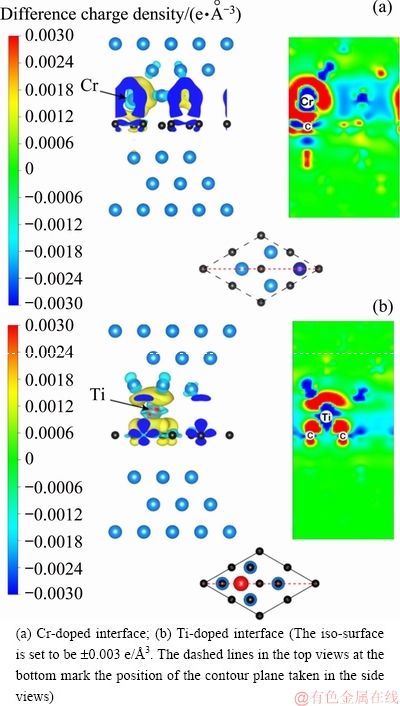
Fig. 4 Difference charge density iso-surfaces and corresponding contours of doped interfaces (Color online)

4 Conclusions

(1) The interface binding energy depends weakly on the interfacial coordination type, but nevertheless, the top-fcc coordinated interface is predicted as the most energy-favored, no matter which interface model and XC functionals are employed.

(2) Both Cr and Ti in Cu bulk have a weak tendency to segregate to the interface. Once it is present on the interface, Cr prefers to occupying the substitutional sites while Ti prefers to occupying the hollow sites.

(3) Both Cr and Ti dopants can greatly strengthen the interface, improving the adhesion by six to ten-folds. The predicted doping effects of Cr or Ti await experimental confirmation.

References

[1] NOVOSELOV, K S, GEIM A K, MOROZOV S V, JIANG D, ZHANG Y, DUBONOS S V, GRIGORIEVA I V, FIRSOV A A. Electric field effect in atomically thin carbon films [J]. Science, 2004, 306(5696): 666-669.

[2] ZHANG X, WANG L, XIN J. Role of hydrogen in graphene chemical vapor deposition growth on a copper surface [J]. Journal of the American Chemical Society, 2014, 136(8): 3040-3047.

[3] BANSZERUS L, SCHMITZ M, ENGELS S. Ultrahigh-mobility graphene devices from chemical vapor deposition on reusable copper [J]. Science Advances, 2015, 1(6): e1500222.

[4] CHEN S, JI H, CHOU H. Millimeter-size single-crystal graphene by suppressing evaporative loss of Cu during low pressure chemical vapor deposition [J]. Advanced Materials, 2013, 25(14): 2062-2065.

[5] LI X, CAI W, AN J. Large-area synthesis of high-quality and uniform graphene films on copper foils [J]. Science, 2009, 324(5932): 1312-1314.

[6] WU T, ZHANG X, YUAN Q H, XUE J C, LU G Y, LIU Z H, WANG H S, WANG H, DING M F, YU Q K, XIE X M, JIANG M H. Fast growth of inch-sized single-crystalline graphene from a controlled single nucleus on Cu-Ni alloys [J]. Nature Materials, 2015, 15: 43-47.

[7] ZHOU H, YU W J, LIU L. Chemical vapour deposition growth of large single crystals of monolayer and bilayer graphene [J]. Nature Communications, 2013, 4(3): 2096-2113.

[8] LIU X, LUO H, SU X, YU Z M. Preparation of diamond/Cu microchannel heat sink by chemical vapor deposition [J] Journal of Central South University, 2015, 22: 835-841.

[9] AVOURIS P. Graphene: Electronic and photonic properties and devices [J]. Nano Letters, 2010, 10(11): 4285-4294.

[10] SCHWIERZ F. Graphene transistors: status, prospects, and problems [J]. Proceedings of the IEEE, 2013, 101(7): 1567-1584.

[11] NOVOSELOV K S, MOROZOV S V, MOHINDDIN T M G. Electronic properties of grapheme [J]. Physica Status Solidi (b), 2007, 244(11): 4106-4111.

[12] SU C Y, LU A Y, XU Y. High-quality thin graphene films from fast electrochemical exfoliation [J]. ACS Nano, 2011, 5(3): 2332-2339.

[13] GIOVANNETTI G. Doping graphene with metal contacts [J]. Physical Review Letters, 2008, 101(2): 026803.

[14] PI K, MCCREARY K M, BAO W. Electronic doping and scattering by transition metals on graphene [J]. Physical Review B, 2009, 80(7): 075406.

[15] KARPAN V M, GIOVANNETTI G, KHOMYAKOV P A. Graphite and graphene as perfect spin filters [J]. Physical Review Letters, 2007, 99(17): 176602.

[16] XU Z, BUEHLER M J. Interface structure and mechanics between graphene and metal substrates: A first-principles study [J]. Journal of Physics: Condensed Matter, 2010, 22(48): 485301.

[17] FUENTES-CABRERA M, BASKES M I, MELECHKO A V. Bridge structure for the graphene/Ni(111) system: A first principles study [J]. Physical Review B: Condensed Matter, 2008, 77(3): 035405.

[18] KHOMYAKOV P A, GIOVANNETTI G, RUSU P C. First-principles study of the interaction and charge transfer between graphene and metals [J]. Physical Review B: Condensed Matter, 2009, 79(19): 195425.

[19] HIROTA K, MITANI. Simultaneous synthesis and consolidation of chromium carbides (Cr₃C₂, Cr₇C₃ and Cr₂₃C₆) by pulsed electric- current pressure sintering [J]. Materials Science and Engineering A, 2005, 399(1): 154-160.

[20] ZHANG H, LI F, JIA Q. Preparation of titanium carbide powders by sol-gel and microwave carbothermal reduction methods at low temperature [J]. Journal of Sol-Gel Science and Technology, 2008, 46(2): 217-222.

[21] REN S, HONG Q, CHEN J. The influence of matrix alloy on the microstructure and properties of (flake graphite+diamond)/Cu composites by hot pressing [J]. Journal of Alloys and Compounds, 2015, 652: 351-357.

[22] WEBER L, TAVANGAR R. On the influence of active element content on the thermal conductivity and thermal expansion of Cu-X (X=Cr, B) diamond composites [J]. Scripta Materialia, 2007, 57(11): 988-991.

[23] MI X, MEUNIER V, KORATKAR N. Facet-insensitive graphene growth on copper [J]. Physical Review B, 2012, 85(15): 1279-1284.

[24] BLOCHL P E. Projector augmented-wave method [J]. Physical Review B: Condensed Matter, 1994, 50(24): 17953-17979.

[25] PERDEW J P, BURKE K, ERNZERHOF M. Erratum. Generalized gradient approximation made simple [J]. Physical Review Letters, 1998, 77(18): 3865-3868.

[26] KRESSE G, FURTHMULLER J. Vienna ab-initial simulation package [EB/OL] [2017-06-16]. http://cms.mpi.univie.ac.at/vasp/ vasp/vasp.html.

[27] KOHN W, SHAM L J. Self-consistent equations including exchange and correlation effects [J]. Physical Review A, 1965, 140(4): 1133-1138.

[28] PAULING L. The nature of the chemical bond and the structure of molecules and crystals: An introduction to modern structural chemistry [M]. New York: Cornell University Press, 1960.

[29] DAVEY W P. Precision measurements of the lattice constants of twelve common metals [J]. Physical Review, 1925, 25(6): 753-761.

[30] PACK J D, MONKHORST H J. Special points for Brillouin-zone integrations—A reply [J]. Physical Review B: Condensed Matter, 1977, 16(4): 1748-1749.

[31] ADAMSKA L, LIN Y, ROSS A J. Atomic and electronic structure of simple metal/graphene and complex metal/graphene/metal interfaces [J]. Physical Review B: Condensed Matter, 2012, 85(19): 2202-2208.

[32] NONG Z, CUI P, ZHU J, ZHAO R D. Alloying effects of V on stability, elastic and electronic properties of TiFe₂via first-principles calculations [J]. Journal of Central South University, 2017, 24: 1551-1559.

[33] THOMAS C, LUC H. From carbon atom to graphene on Cu(111): An ab-initio study [J]. European Physical Journal B, 2015, 88(2): 1-5.

[34] LAN G, JIANG Y, YI D. Theoretical prediction of impurity effects on the internally oxidized metal/oxide interface: the case study of S on Cu/Al₂O₃ [J]. Physical Chemistry Chemical Physics, 2012, 14(31): 11178-11184.

[35] YONG J, SMITH J R, EVANS A G. First principles assessment of metal/oxide interface adhesion [J]. Applied Physics Letters, 2008, 92(14): 141918.

Cr、Ti掺杂Cu/石墨烯界面结合性能的第一性原理预测

刘 洋^1,2，王 刚¹，王怡人¹，江 勇^1,3，易丹青¹

1. 中南大学 材料科学与工程学院 有色金属材料科学与工程教育部重点实验室，长沙 410083；

2. School of Materials Science and Engineering, University of Pennsylvania, Philadelphia 19104, USA;

3. 中南大学 粉末冶金国家重点实验室，长沙 410083

摘  要：基于密度泛函理论，对过渡金属Cr、Ti掺杂的Cu/石墨烯界面结合性能进行第一性原理预测，构建并对比一系列不同Cu/石墨烯界面的三明治和表面模型。计算结果表明，界面位相关系对界面结合强度影响不大。两种界面模型的计算结果均显示top-fcc配位模型是最稳定的界面结构，并具有较低的界面结合能。Cr掺杂倾向于偏析到界面上取代Cu，而Ti惨杂倾向于占据界面处的填隙位。虽然这两种元素的偏析趋势都较弱，其偏析可以显著提高界面的结合性能，从而强化界面。

关键词：铜；铬；钛；石墨烯；掺杂；界面；第一性原理

(Edited by Wei-ping CHEN)

Foundation item: Project (2018YFE0306100) supported by the National MCF Energy R&D Program of China

Corresponding author: Yi-ren WANG, E-mail: yiren.wang@csu.edu.cn; Yong JIANG, E-mail: yjiang@csu.edu.cn

DOI: 10.1016/S1003-6326(19)65079-X

Abstract: We presented a density functional theory study on doping effects of transition metals (Cr and Ti) on the Cu/graphene interface adhesion. Various undoped Cu/graphene interface structures were constructed using both the sandwich and the surface models. Energetics calculations showed that the interface binding strength only weakly depends on interface coordination. Both interface models predicted the top-fcc coordination type as the most energy-favored, with a low binding energy value. Segregated Cr prefers to substituting for Cu, while Ti occupies a hollow site at the interface. Although the segregation tendencies are both very weak, once present on the interface, both dopants can greatly increase the interface binding energy and improve the adhesion.