中南大学学报(英文版)

J. Cent. South Univ. (2019) 26: 728-742

DOI: https://doi.org/10.1007/s11771-019-4043-5

Dynamic stress accumulation model of granite residual soil under cyclic loading based on small-size creep tests

TANG Lian-sheng(汤连生)^{1, 2}, ZHAO Zhan-lun(赵占仑)^{1, 2}, CHEN Hao-kun(陈浩坤)^{1, 2},WU Yan-ping(巫燕萍)^{1, 2}, ZENG Yu-chao(曾玉超)^{1, 2}

1. School of Earth Sciences and Engineering, Sun Yat-sen University, Guangzhou 510275, China;

2. Guangdong Provincial Key Lab of Geodynamics and Geohazards, Guangzhou 510275, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract:

The creep behaviors of granite residual soil with pre-stress of 100 kPa was investigated by a series of small size creep tests. Three different types of strain curves were obtained at different stress levels. Based on creep characteristics of the granite residual soil under different stress levels, a creep model of the granite residual soil was established by rheological theory, and related parameters of the model were determined according to the experimental data at the same time. Further on, based on the established creep model, a theoretical model of dynamic stress accumulation in the granite residual soil under cyclic loading was deduced. It is found that there is a threshold of dynamic stress accumulation in this theoretical model. The dynamic stress accumulation laws of the granite residual soil are different under different cyclic loading stress. Finally, with the dynamic stress accumulation laws in the small-size samples of granite residual soil under different cycle loading studied and the experimental results comparing with the theoretical results, it verifies the validity of the theoretical model.

Key words:

granite residual soil; creep tests; dynamic stress accumulation model；

Cite this article as:

TANG Lian-sheng, ZHAO Zhan-lun, CHEN Hao-kun, WU Yan-ping, ZENG Yu-chao. Dynamic stress accumulation model of granite residual soil under cyclic loading based on small-size creep tests [J]. Journal of Central South University, 2019, 26(3): 728–742.

DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-019-4043-5

1 Introduction

The dynamic stress in the subgrade soil is an additional stress caused by the dynamic load of the vehicle, which is a response of the subgrade material to a stress increment of the dynamic load [1]. TANG et al [2–4] have been aware that under the repeated vehicle dynamic load, the dynamic stress in the material of the road structure and the subgrade soil does not disappear completely with the moving load of the vehicle removed, instead a part of dynamic stress will be saved, which is called residual stress. The residual stress in the subgrade soil will accumulate and superimpose on the subsequent dynamic additional stress response, which will add to the additional dynamic stress under the load of the vehicle. Therefore, the existence of residual stress in the roadbed and foundation soil under its continuous accumulation will accelerate the creep deformation and the settlement of the road structures, even to affect the driving comfort so as to traffic accidents easily [5–7]. Hence, due attention should be paid to the dynamic stress accumulation phenomenon of the road structures.TANG Lian-sheng and ZHAO Zhan-lun contributed equally to this work.

In recent years, some in-situ monitoring tests [8], site tests [1, 9, 10] and model tests [11–16] have been carried out as a series of studies on residual stress and dynamic stress accumulation in subgrade soil and pavement cushion; besides, TANG et al [8] monitored the presence of dynamic stress responses in the soft subgrade of the Shanghai subway under traffic conditions; further monitoring data from SHOOP et al [10] showed that the residual dynamic stress of the cohesive soil subgrade out of the dynamic stress response accumulates with the increased repetitions of the load. In addition, the site test results showed that even if the vehicle load remains constant, the peak stress in the cohesive soil increases with growing load repetitions [1, 9]. The full-size model tests simulated the dynamic response of the high plastic limit silty clay subgrade of the airstrip [12], the stabilized soil foundation of highway cement [11] and the granite residual soil subgrade of the road [14] under repeated load, the results of those tests showed that the peak stress in the subgrade soil gradually built up during the initiation of loading. The studies above verify the existence of residual stress in subgrade soil, meanwhile work out the law of stress accumulation and peak stress. With the research deepened, more rules have also been found out. THAKUR et al [13] carried out the cycle plate loading tests on the pavement base, resulting in that the peak stress in the sandy subgrade interface rapidly increased in the first few loading cycles, afterwards stabilized to a certain value or continued to increase until getting damaged. TAFRESHI et al [16] carried out a cyclic plate load test on a rubber-concrete mixed soil to monitor the peak stress response in the soil; as a result, the peak stress was continuously increased together with the increase of the cyclic loading. SUN et al [15] carried out a cyclic plate loading test on the pavement base as well to monitor the vertical stress response and lateral stress response in the subgrade soil, which turns out that under low cyclic loading, the stress response in the soil is relatively stable; but under high cyclic loading, the vertical and lateral stress responses in the soil increase obviously with the increase of the number of cycles. ABDELKRIM et al [17], ALAKUKKU et al [18] and TANG et al [1] explained the phenomenon of this peak stress response increase: the residual stress accumulates and superimposes onto subsequent loading cycles; the stress responses increase with the increase of the loading times; and the dynamic stress accumulation in the subgrade soil plays a key role in the change of the peak stress. However, the existing research is mainly aimed at the residual stress and the change of the peak stress in the subgrade soil. Although the dynamic stress accumulation phenomenon has been noticed, there has been no due attention and in-depth study. It is very necessary to systematically study the dynamic stress accumulation phenomenon both from the theoretical and model point of view.

The residual stress in the material is related to its microstructure [19, 20], especially as a kind of typical stick elastic-plastic material, the soil has different mechanical properties, which is liable to cause residual stress in the soil due to deformation coordination between mineral grains. The cumulative deformations of the soil include permanent plastic deformation and unrecovered elastic deformation, in return these deformations affect the change of residual stress in the soil upon unloading. Therefore, to deepen the understanding of the cumulative effect on dynamic stress in soil, it is worthy to systematically explore the deformations of soil. This paper studies the complete rheological process of the subgrade soil during the loading and unloading processes by rheological method; distinguishes the various kinds of strain of the subgrade in the process of compressive loading; establishes the rheological constitutive model of the subgrade soil in vertical direction according to the characteristics of strain composition; and deduces the dynamic stress accumulation constitutive relation of the granite residual soil under cyclic loading according to the established rheological constitutive model and experimental data. In addition, the model parameters are determined experimentally and the experimental data are compared with the model predictive data, verifying the validation of the dynamic stress accumulation model under cyclic loading. In this work, the stress accumulation reasons and stress accumulation laws of the subgrade soil are illustrated from the mechanism perspective, which can help to demonstrate the essence of the stress accumulation in the subgrade soil and establish the constitutive model describing the vertical stress accumulation of the subgrade soil.

2 Small-size creep tests of granite residual soil

The dynamic stress accumulation in the subgrade soil is intrinsically related to the residual strain after unloading. The residual stress in the soil results from the rotation, displacement and deformation of the soil particles under external loading [21]. In other words, the residual stress in the soil and the deformation after soil unloading are symbiotic. As a granular material with viscous characteristics, the deformation of the soil caused by external loading is time-dependent [22–24]. Under normal circumstances, it can be observed that after unloading, irreversible deformation and recoverable rebound deformation of the soil would happen; as well it shall be noted that the characteristics including viscous flow, and elastic aftereffects are extremely obvious in loose and weak soil [25–27]. These characteristics determine the deformation behavior of soil after unloading, thus affecting the changes of residual stress in soil. Many geotechnical tests have observed that the resilient deformation of the soil is not fully restored at the moment of unloading and exhibits time-dependent “elastic aftereffect” [28].

As shown in Figure 1, a cyclic loading test with a load of 20 kPa is firstly carried out on the granite residual soil with a pre-stress of 100 kPa in this study. The dynamic stress of the granite residual soil at 0.5H (H is the height of sample) increases linearly with the increase of the loading times; there is accumulation for the axial strain in synchronism with stress accumulation. During dynamic loading and unloading, the dynamic stress changes with the axial strain. QIAN et al [29] performed a series of cyclic triaxial undrained tests on Shanghai clay, the results show that the correlation of the increment per cycle of permanent axial strain and the area of hysteretic loop per cycle of energy dissipation is close. The dynamic stress accumulation in the subgrade soil may be due to the fact that the kinetic energy part is preserved in the soil due to the strain. In order to study the dynamic characteristics of soil dynamic stress, we must first understand the creep characteristics of soil; identify the composition of the creep deformation which causes stress accumulation in the soil, furthermore build up the stress accumulation model by the stress–strain relationship. Based on this understanding, this work carried out the creep test of granite residual soil, exploring its creep characteristics and distinguishing its creep components.

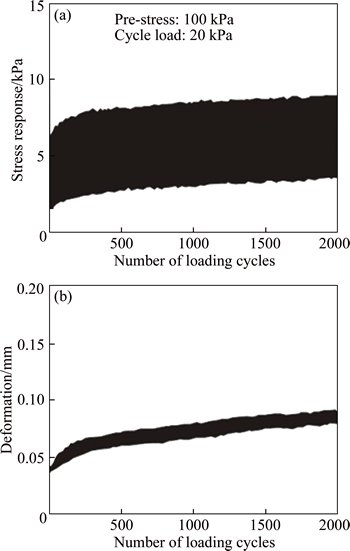
Figure 1 Comparison between axial stress response (a) and axial deformation (b) of granite residual soil at 0.5H (H is height of sample) under cycle load of 20 kPa

2.1 Introduction to experimental materials

The physical properties and mechanical indexes of the granite residual soil in natural state (Figure 2) collected from a site in Guangzhou Metro Line 21 are shown in Tables 1 and 2, respectively.

2.2 Creep tests

In order to simulate the true pressure state of the roadbed, the selected granite residual soil was pre-compacted at 100 kPa before the test and formulated into the test soil samples with diameter of 15.2 cm and height of 10 cm. The circular area with a diameter of 5 cm acts as a compression zone, as shown in Figure 3.

Figure 2 Granite residual soil in natural state

Table 1 Physical properties of granite residual soil in natural state

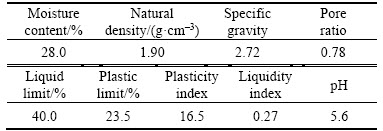
Table 2 Main mechanical indicators of granite residual soil in natural state

Creep tests and dynamic stress accumulation tests are carried out by self-designed cyclic loading test system, and the test device is shown in Figure 4.

Creep tests include a loading stage and an unloading stage (shown in Figure 5), the loading stage of creep tests carried out using single-stage load. The test results with typical creep characteristics are shown in Figure 5.

According to the comparisons of experimental results of different stress levels, the following conclusions can be drawn: 1) Under low stress level, instantaneous strain would happen to the granite residual soil; 2) Under less low stress level,instantaneous strain and deceleration creep would happen to the granite residual soil; 3) Under high stress level, the instantaneous strain, deceleration creep and steady-state creep would occur to granite residual soil.

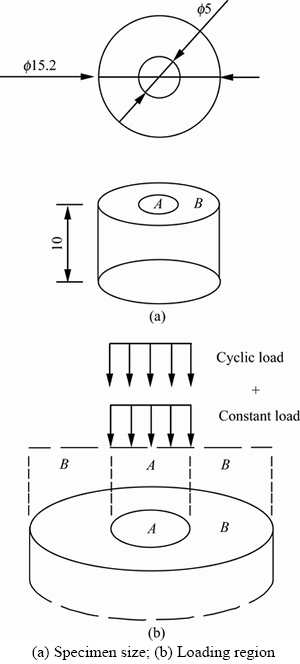
Figure 3 Schematic diagram of test soil sample: (Unit: mm):

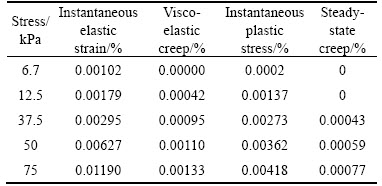
According to the characteristics of unloading- rebound test data, the axial strain components at all stress levels are decomposed and the decomposition method is similar to that of rock creep test [30]. Figures 6–8 show the measured strain value of the granite residual soil and the corresponding creep composition under different stress conditions. When the loading stress σ≤6.7 kPa, the granite residual soil gives only instantaneous strain, whose loading– unloading creep characteristics are shown in Figure 6; when the loading stress 6.7 kPa<σ≤12.5 kPa, the granite residual soil will occur instantaneous strain (including elastic strain and plastic strain) and visco-elastic creep, the axial total strain curve and the visco-elastic creep curve at loading stage are shown in Figure 7; when σ>12.5 kPa, the granite residual soil generates instantaneous strain, visco-elastic creep and steady-state creep, whose different creep components characteristics are shown in Figure 8.

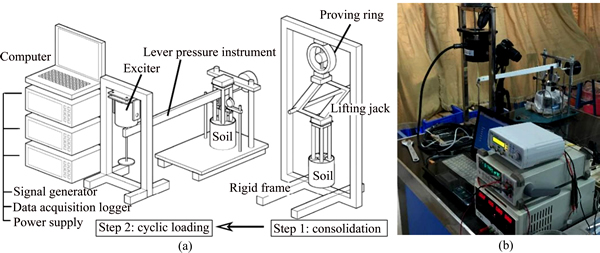
Figure 4 Schematic diagram (a) and photo (b) of cyclic loading test system

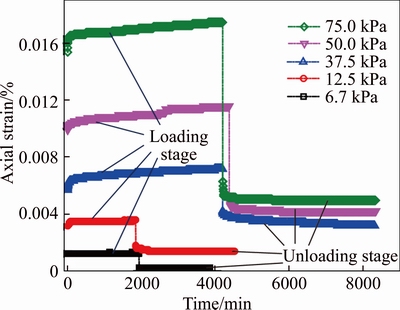
Figure 5 Creep test results of granite residual soil under different stress conditions

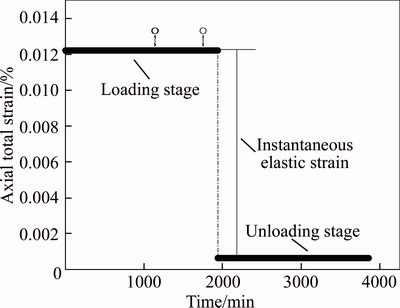
Figure 6 Granite residual soil loading–unloading creep curve and creep components decomposition under loading stress of 6.7 kPa

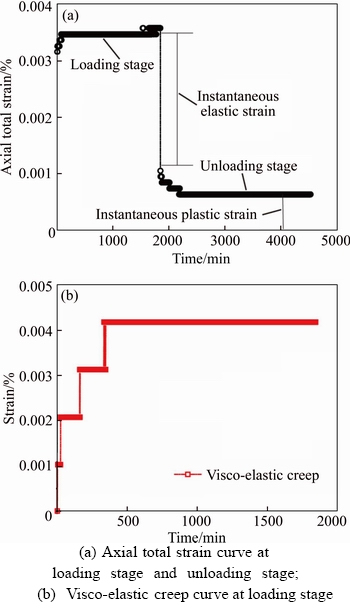
Figure 7 Granite residual soil loading-unloading creep curve and creep components decomposition under loading stress of 12.5 kPa:

Based on the analysis of the measured loading–unloading creep data, the strain composition of the granite residual soil under different stress conditions is divided and the results are summarized in Table 3.

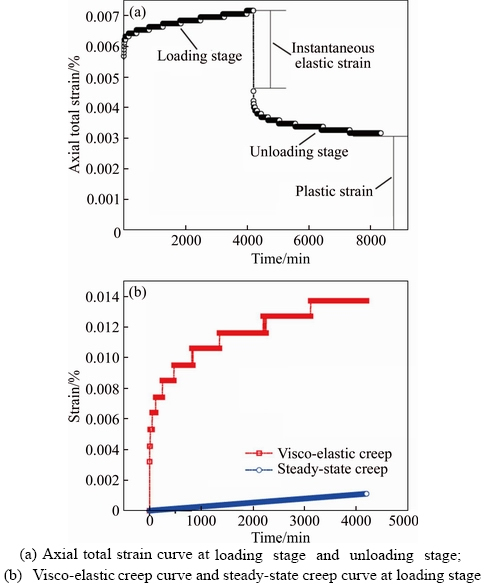
Figure 8 Granite residual soil loading–unloading creep curve and creep components decomposition under loading stress of 37.5 kPa:

Table 3 Strain composition of granite residual soil under different stress conditions

3 Nonlinear creep model of granite residual soil

3.1 Strain components

According to the test results (Table 3) under varied loading–unloading conditions, it shows that the granite residual soil’s overall creep deformation consists of the following deformation components:

1) The instantaneous strain response. At all levels of stress, the granite residual soil generated the instantaneous strain ε₀ during loading; once unloaded, the instantaneous elastic strain was generated,indicates that the instantaneous strain includes instantaneous elastic strainand instantaneous plastic straiThe instantaneous deformation can be described by the Hooke model, but in the unloading process, the instantaneous plastic, strain is attributed to irreversible deformation. The granite residual soil creep model contains a resilient Hooke element.

2) Attenuation creep. When the stress value is higher than σ₁ (6.7 kPa in this work), the attenuation creep occurs on the basis of the instantaneous strain by analyzing the loading and unloading rebound creep curve. It can be found that the partial strain is a visco-elastic strain ε₁(t), which can be fully restored after unloading for a certain period of time. The creep model of the granite residual soil contains a Kelvin element in parallel with the St. Venant element.

3) Steady-state creep. When the load is higher than σ₂ (12.5 kPa in this paper), in addition to instantaneous strain, visco-elastic creep, also a linear growing creep over time would be produced; the part of the creep will not be recovered after unloading, which is unrecoverable plastic strain, as shown in Figure 8(b). This stage can be described by the viscoplastic element Bingham element.

3.2 Nonlinear creep model

According to the above analysis, the creep characteristics of granite residual soil can be described by visco-elastic-plastic creep model, as shown in Figure 9.

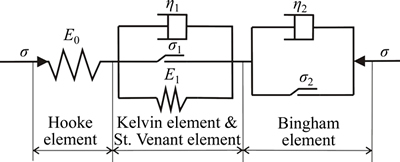
Figure 9 Schematic diagram of one-dimensional creep model of granite residual soil

At the loading stage, the one-dimensional stress–strain constitutive equation of granite residual soil can be established under three kinds of stress conditions according to the above model (Figure 9), which is as follows:

1) When the axial stress σ≤σ₁, only the Hooked element in Figure 9 produces instantaneous deformation, because the instantaneous strain contains the instantaneous elastic strain and instantaneous plastic strain, that is whose instantaneous deformation during loading stage can be described by Hooked element; but in the unloading stage, the rebound shall be distinguished between elastic and plastic parts, with the constitutive equation listed below:

                               (1)

where σ₀ is the applied loading stress, E₀ is the elastic modulus of the Hooked element.

2) When σ₁<σ≤σ₂, the Hooked element and the Kelvin element which is in parallel with the friction element ( St. Venant element) generate deformation, can describe the instantaneous strain and decay creep stage, the rheological differential constitutive equation is:

    (2)

When loading stress σ=σ₀, the creep equation is obtained by solving the differential constitutive Eq. (2) according to the initial condition as:

                  (3)

where E₁ and η₁ are separately the elastic modulus and viscosity coefficient of Kelvin element, σ₁ works as the threshold of Kelvin element.

3) When σ>σ₂, the Hooked element and the Kelvin element which is in parallel with the friction element and the Bingham element are all involved in the deformation, which can describe the instantaneous strain, decay creep and linear creep of the granite residual soil. The rheological differential equation is:

 (4)

When σ=σ₀, the creep equation is obtained by solving the differential constitutive Eq. (4) according to the initial condition as:

          (5)

where η₂ is the viscosity coefficient of Bingham element, σ₂is the threshold of Bingham element, and the rest parameters are the same as above.

3.3 Elastic aftereffect equation

According to the established model in this work, when unloaded to 0 at the time of t=t_n, the elastic aftereffect equation under the above three kinds of stress conditions can be obtained:

1) In the case of σ₀≤σ₁, asthe Hooked element produces instantaneous elastic recovery strain, meanwhile preserves the instantaneous plastic strain. The elastic aftereffect equation is:

                     (6)

2) When σ₁<σ₀≤σ₂, at the moment the stress is unloaded to 0 kPa, the total amount of visco-elastic creep produced by the model is the plastic strain produced is Assuming that the decay creep process follows the same path as the elastic recovery process, the elastic aftereffect equation is:

    (7)

3) When σ₀>σ₂, the loading stress becomes 0 at the time t=t_n, the total amount of viscoelastic creep isthe plastic strain includes the transient plastic strain and the resulting plastic strain from Bingham elementWith the decay creep process assumed to be the same as the creep recovery process, the elastic aftereffect equation after unloading is:

  (8)

3.4 Parameters of nonlinear creep model of granite residual soil

1) The instantaneous elastic modulus E₀. Known from the creep model, the instantaneous

strain can be described by According to the creep test data, the instantaneous elastic modulus E₀ of the granite residual soil with 100 kPa pre-stress under different stress conditions can be obtained, as shown in Table 4.

Table 4 Measured parameters of granite residual soil with pre-stress of 100 kPa under different stress levels

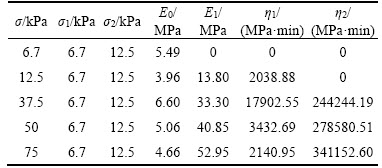
2) Decay creep parameters E₁, σ₁ and η₁. In the creep model, the visco-elastic decay creep can be described byand the formula is applied to the stress conditions of 12.5, 37.5, 50 and 75 kPa, respectively, whose visco- elastic attenuation creep scatter plots have been fit and the fitting curves are shown in Figure 10. According to the fitting parameters and the σ₁ determined by the creep tests, the decay creep parameters under the above four different stress levels can be obtained, as shown in Table 4.

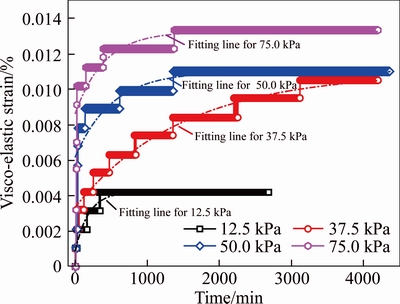
Figure 10 Visco-elastic decay creep fitting curve at loading stage

3) Steady-state creep parameters η₂ and σ₂ (shown in Table 4). According to the creep model, the steady-state creep of granite residual soil can be described by and η₂ can be determined by using this formula to fit the creep test data at the stress levels of 37.5, 50 and 75 kPa. The value of σ₂ is 12.5 kPa according to the results of the creep tests.

4 Stress accumulation model

4.1 Axial strain distribution along axis direction of specimen

In the cyclic loading model tests, the vertical strain in the soil sample is different at different heights. Assuming that the vertical deformation (not the settlement) of each layer on the axis of the granite residual soil sample distributes in a shape of inverse elliptical arc, the elliptic equation is x²/a²+y²/b²=1 (where a and b are the major axis and minor axis of the elliptical respectively), as shown in Figure 11(b).

Based on the above assumption, the vertical settlement D(h) of the granite residual soil sample at the depth h(h is the vertical distance from the stress acting surface) can be approximately equal to the sum of the deformation of each layer from the depth H to h of the sample(shown in Figure 11(b)). Therefore, the expression of D(h) at the depth h of the granite residual soil specimen can be expressed as:

                (9)

The total vertical settlement S of the sample is the total deformation from the depth 0 to H, and that is the area of the shadow area in Figure 11(b) given as:

                  (10)

Formula (10) can be transformed into and formula (11) can be obtained by substituting into the formula (9).

         (11)

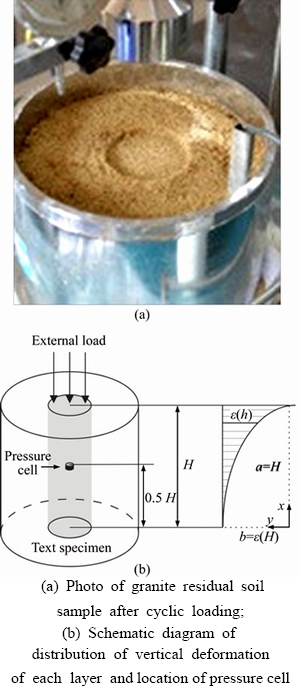
Figure 11 Schematic diagram about distribution shape of vertical deformation of each layer on axis of granite residual soil sample:

where H is the height of the test sample, and the height of the granite residual soil sample with the pre-stress of 100 kPa is 10 cm in this study. So the settlement of the sample at the height of 0.5H (the location of the pressure cell is used to measure the stress in the sample, as shown in Figure 11(b)) is given as:

          (12)

and the strain could be expressed as:

            (13)

4.2 Dynamic stress growth model at loading stage

As shown in Figure 1, the instantaneous strain of the granite residual soil happens at the moment of being loaded, and the creep deformation accumulatively increases before unloading. Corresponding to the occurrence of strain is the instantaneous stress increment occurred in the soil at the moment of loading, and the occurrence of creep is accompanied by the increasing stress. The stress growth in the soil is caused by the internal elasticity and plastic strain of the granite residual soil, leading to the continuous accumulation of energy in the soil. Therefore, the stress–strain relationship should also satisfy the constitutive differential Eqs. (1), (2) and (4). Based on the above understanding, the creep formula at the depth 0.5H of the sample determined by formula (13) is substituted into the differential Eqs. (1), (2) and (4) respectively. After solving the differential equations, the stress growth model of the granite residual soil at the depth of 0.5H under different loading conditions is obtained.

1) When σ₀≤σ₁, the stress growth model of granite residual soil at the depth 0.5H is:

σ(t)=0.1011·ε₀E₀                                       (14)

2) When σ₁<σ₀≤σ₂, the stress growth model of granite residual soil at the depth 0.5H is:

                     (15)

whereB is the parameter determined according to the initial conditions.

3) When σ>σ₂, the stress growth model is

                (16)

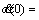
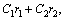
where r₁, r₂= the initial condition is: when t=0, the internal stress of the soil is σ(0)=C₁+C₂+σ₂ (measured value), C₂=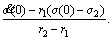

4.3 Dynamic stress release model at unloading stage

As to the model shown in Figure 9, when t=t_n and the cyclic loading unloaded to 0 kPa, the stored energy of the instantaneous deformation can be dissipated immediately after unloading; the stored energy of the visco-elastic deformation can be gradually dissipated after unloading; the energy stored in the plastic strain can be stored inside the soil. The different ways of energy dissipation appear as the instantaneous stress reduction → the attenuation reduction → the partial storage of the stress, the stress–strain relationship should satisfy the constitutive differential Eqs. (2) and (5), but the constitutive equation is not continuous for the process from the loading stage to the unloading stage, as it contains the instantaneous elastic strain produced by the Hooke element, the instantaneous elastic stress caused by the instantaneous elastic strain shall be removed when deducing the internal stress release model according to the creep equation; i.e.(is the instantaneous elastic stresses produced by the Hooke element). In this study, the pressure cell is embedded at the axial depth 0.5H of the sample, so the strain ε(0.5H)= 0.1011·ε(t–t_n); with 0.1011·ε(t–t_n) submitted to formulas (1), (2) and (4), respectively, and σ in the constitutive equation would be changed into . By solving the constitutive equations, the internal stress release model of the granite residual soil at the unloading stage is:

1) When σ₀≤σ₁, the stress release model at depth 0.5H of the granite residual soil samples is:

                    (17)

2) When σ₁<σ₀≤σ₂, the stress release model can be expressed as:

               (18)

where G is the constant determined by the internal stress of the soil at the moment of unloading; and other parameters are the same as above.

3) When σ₀>σ₂, andwould be submitted into formula (7), the stress release differential equation in the soil at the unloading stage would be obtained:

       (19)

Through solving differential Eq. (19), the stress release formula would be obtained:

    (20)

including r₁,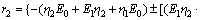when t=0 as the initial condition, the internal stress in soil is (measured value),

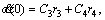
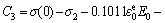
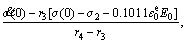
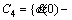
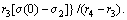
4.4 Dynamic stress accumulation model

The model formulas obtained in Sections 4.2 and 4.3 of this paper can describe the stress growth process during loading stage and the stress release process during unloading stage respectively. The difference value between the stress increment and the stress release value is equal to the stress accumulation value in a loading–unloading cycle. The sum of the difference value △σ_n in each loading–unloading cycle is the total stress accumulation value △σ in soil, i.e., △σ=△σ₁+△σ₂+…+△σ_n, but there are some differences in the stress accumulation under different stress levels, stated as follows:

1) When σ₀≤σ₁, the internal stress growth model (14) and the internal stress release model (17) at depth 0.5H of the granite residual soil samples are constant with time, hence it can be judged that under this stress level, the stress growth and release are completed in an instant, the stress release value △σ_r at the first loading–unloading cycle is:

                         (21)

The size of △σ_r is determined by the instantaneous elastic part of the instantaneous strain, the granite residual soil preserves the stress generated from the instantaneous plastic part of the instantaneous strain, i.e., According to formula (14), from the second loading–unloading cycle, the increase in stress is at the loading stage, and it can be completely restored at the moment of unloading, i.e., △σ_n=0 (n≥2), and the total stress accumulation value △σ=△σ₁. When cyclic loading stress is 6.7 kPa, i.e., σ₀=6.7 kPa, the theoretical results of the internal stress accumulation of the granite residual soil sample at the depth 0.5H are shown in Figure 10 (the parameters involved in the formula are listed in Tables 3 and 4). There are 5 loading– unloading cycles in Figure 10, the time of loading stage is 180 s and unloading stage is the same.

2) When σ₁<σ₀≤σ₂, the internal stress growth model (15) and the internal stress release model (18) illustrate the stress growth and release are the functions of time t. If unloading is conducted when t=t_n, the stress release value is:

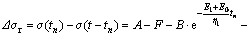
                        (22)

From formula (22), it can be seen that the stress release after unloading is not completed in an instant, but a function of time change. If the time of unloading is not enough to release all the stress, partial elastic stress will be stored inside the soil, that is △σ_n>0, and the value of △σ_n can be calculated using formula (18); with the number of cyclic loading–unloading increasing, △σ=△σ₁+△σ₂+…+ △σ_n will continue to increase, and the stress will continue to accumulate; where △σ₁ includes irrecoverable stress and unresolved elastic stress from the instantaneous strain stored in the soil, △σ_n (n≥2) is the elastic stress that has not yet been restored only. Figure 13 shows the theoretical results of stress accumulation with σ₀=12.5 kPa, the time of loading stage and unloading stage are 600 s and 300 s, respectively. B=1.81, G=1.13 which can be obtained from the measured data of cyclic loading–unloading tests. The remaining related parameters are determined by creep test data and listed in Tables 3 and 4.

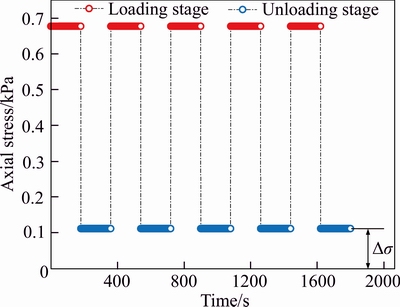
Figure 12 Theoretical results of dynamic stress accumulation at depth 0.5H of granite residual soil sample under cyclic loading–unloading of 6.7 kPa

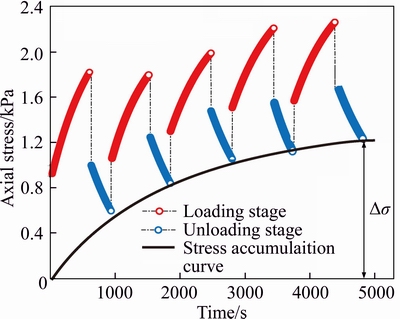
Figure 13 Theoretical results of dynamic stress accumulation at depth 0.5H of granite residual soil sample under cyclic loading–unloading of 12.5 kPa

It is obvious in Figure 13 that the slope of dynamic stress accumulation curve shows a decreasing trend with the number of cyclic loading–unloading increasing and the cumulative stress does not increase infinitely. In fact, according to the theoretical results of the stress growth calculated by the theoretical formula (15) in this paper (Figure 14), the stress increases in a mode of decay. If the loading time is long enough, the stress will tend to be constant. This may be the reason why the slope of stress accumulation curve shows the decay tendency.

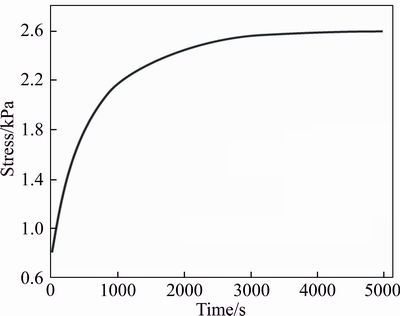
Figure 14 Theoretical curve of stress growth at depth 0.5H of granite residual soil sample under loading stress of 12.5 kPa

3) When σ₀>σ₂, according to the internal stress growth model (16) and the internal stress release model (20), the stress release value can be expressed as:

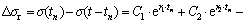
      (23)

According to formula (23), △σ_r is the function of time, and the stress accumulation process is similar to the process of σ₁<σ₀≤σ₂. The value of △σ_n can be calculated using formula (20).

When σ₀=37.5 kPa, the time of loading stage and unloading stage are 600 s and 300 s, respectively, and theoretical results of stress accumulation are shown in Figure 15. The initial conditions can be determined by the experimental data: at the loading stage, σ(0)=7.6 kPa, 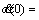0.0026 kPa/s; at the unloading stage, σ(0)=5.5 kPa, 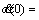–0.0034 kPa/s, and the remaining parameters are determined by the creep tests and listed in Tables 3 and 4.

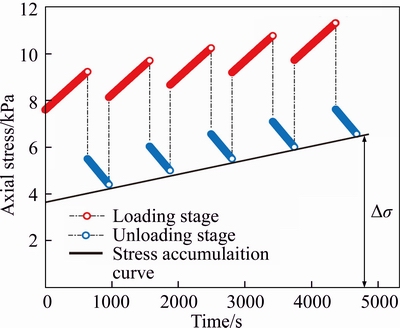
Figure 15 Theoretical results of dynamic stress accumulation at depth 0.5H of granite residual soil sample under cyclic loading–unloading of 37.5 kPa

The stress accumulation curve shown in Figure 15 is close to straight line and different from the accumulation curve of σ₁<σ₀≤σ₂. The reason for the difference can be explained as follow: when σ₀>σ₂, the Bingham element in the creep model (Figure 9) works; with the number of cyclic loading–unloading increasing, there is new plastic deformation in the soil continuously, leading to the stress accumulation increasing.

4.5 Verification of stress accumulation model

In order to verify the validity of the stress accumulation model, the dynamic stress response data at depth 0.5H of granite residual soil sample under cyclic loading–unloading stress of 6.7, 12.5 and 37.5 kPa were measured respectively (shown in Figure 16), and the measured stress accumulation modes under different stress levels are similar to the theoretical modes: when σ₀=6.7 kPa, the dynamic stress accumulation under the cyclic loading– unloading does not occur again except for the first loading, as shown in Figure 16(a); when σ₀=12.5 kPa, the dynamic stress would accumulate in a gradual attenuation mode, as shown in Figure 16(b); when σ₀=37.5 kPa, the dynamic stress is linearly accumulated with the increase of the number of cyclic loading, as shown in Figure 16(c); the comparison between theoretical stress accumulation curve and measured stress accumulation curve are shown in Figure 16. It is obvious that the stress accumulation model of granite residual soil established by creep tests can describe the accumulation law of dynamic stress in soil, verifying the validity of the model established in this paper.

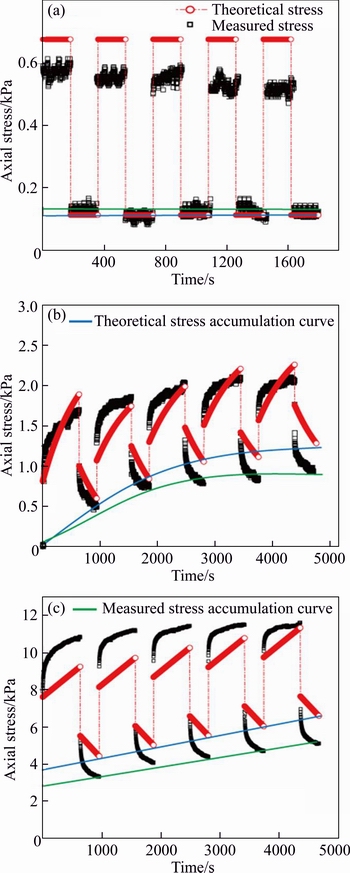
Figure 16 Comparison between measured data and theoretical value under cyclic loading of 6.7 kPa (a),12.5 kPa (b) and 37.5 kPa (c), respectively

As shown in Figure 5, 6.7 kPa and 12.5 kPa are stress thresholds of the creep tests, they are the demarcation points that divide the creep property of granite residual soil. In this paper, the theoretical and measured results of the stress accumulation show that the two thresholds also determine the change of stress accumulation modes. Under the same cyclic loading stress levels, the dynamic stress accumulation law of granite residual soil can well correspond to the creep characteristics.

Of course, the model results and experimental results are not completely coincident, which may be related to possible deviation between the assumptions of strain along the vertical distribution and the reality; and the accuracy of measurement method of the relevant parameters in the model has yet to be further improved.

5 Conclusions

In this work, the creep laws of granite residual soil at different stress levels are studied and the strain components of creep data are divided. Afterwards, the creep model of granite residual soil is established by rheological theory, together the relevant parameters involved in the model are determined according to the model and experiment data. Further on, based on the creep model, the theoretical model of dynamic stress accumulation at the depth 0.5H of granite residual soil sample is deduced. Finally, the dynamic stress accumulation law of the granite residual soil is experimentally studied, and the experimental results are compared with the theoretical results to verify the validity of the theoretical model. Through the research of this paper, the following conclusions could be made:

1) It is feasible to explore the law of dynamic stress accumulation by studying the creep characteristics of granite residual soil.

2) The appearance of dynamic stress accumulation phenomenon needs to meet initial stress conditions and appropriate loading–unloading frequency, and the dynamic stress accumulation law of the granite residual soil changes with the stress levels of the cyclic loading.

3) The stress thresholds that determine the dynamic stress accumulation law are consistent with the thresholds of the creep tests, and the stress accumulation law changes with the creep regularity simultaneously, which indicates that the occurrence of stress accumulation is caused by the deformation of the soil material; however, the occurrence of strain does not necessarily cause stress accumulation.

Nomenclature

σ₀

Applied loading stress, kPa

σ₁

Threshold of Kelvin element, kPa

σ₂

Threshold of Bingham element, kPa

ε₀

Instantaneous strain, %

Instantaneous elastic strain, %

Instantaneous plastic strain, %

ε₁(t)

Visco-elastic strain, %

ε₂(t)

Plastic strain of Bingham element, %

△σ_r

Stress release value, kPa

△σ

Sum of the stress accumulation amounts, kPa

E₀

Elastic modulus of the Hooked element, MPa

E₁

Elastic modulus of Kelvin element, MPa

η₁

Viscosity coefficient of Kelvin element (MPa·min)

η₂

Viscosity coefficient of Bingham element, (MPa·min)

References

[1] TANG Lian-sheng, CHEN Hao-kun, SANG Hai-tao, ZHANG Si-yang, ZHANG Jie-yi. Determination of traffic-load-influenced depths in clayey subsoil based on the shakedown concept [J]. Soil Dynamics and Earthquake Engineering, 2015, 77(1): 182–191. DOI: https://doi.org/ 10.1016/j.soildyn.2015.05.009.

[2] TANG Lian-sheng, ZHANG Qing-hua，LIAO Hua-rong. Advance in post-construction settlement of soft subgrade soil [J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 3449–3455. DOI: 10.3321/j.issn:1000- 6915.2006.z2.016. (in Chinese)

[3] TANG Lian-sheng, XU Tong, LIN Pei-yuan, YU Hai-tao. Studies on dynamic stress characters of layered road system under traffic loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S2): 3876–3884. DOI: 10.3321/ j.issn:1000-6915.2009.z2.084. (in Chinese)

[4] TANG Lian-sheng, ZHANG Qing-hua, YIN Jing-ze, WU Yu-gang, LIAO Hua-rong. Accumulated behavior of subgrade clay under traffic lading [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2007, 46(6): 143–144. DOI: 10.3321/j.issn:0529-6579. 2007.06.033. (in Chinese)

[5] CUI Xin-zhuang, ZHANG Na, ZHANG Jiong, GAO Zhi-jun. In situ tests simulating traffic-load-induced settlement of alluvial silt subsoil [J]. Soil Dynamics and Earthquake Engineering, 2014, 58(1): 10–20. DOI: https://doi.org/ 10.1016/j.soildyn. 2013.11.010.

[6] WERKMEISTER S, DAWSON A R, WELLNER F. Permanent deformation behaviour of granular materials [J]. Road Materials and Pavement Design, 2005, 6(1): 31–51. DOI: https://doi.org/10.1080/14680629.2005.9689998.

[7] PUPPALA A J, SARIDE S, CHOMTID S. Experimental and modeling studies of permanent strains of subgrade soils [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(10): 1379–1389. DOI: 10.1061/(ASCE)GT.1943- 5606.0000163.

[8] TANG Yi-qun, CUI Zheng-dong, ZHANG Xi, ZHAO Shu-kai. Dynamic response and pore pressure model of the saturated soft clay around the tunnel under vibration loading of Shanghai subway [J]. Engineering Geology, 2008, 98(3, 4): 126–132. DOI: https://doi.org/10.1016/j.enggeo.2008.01. 014.

[9] WIERMANN C, WAY TR, HORN R, BAILEY A C, BURT E C. Effect of various dynamic loads on stress and strain behavior of a Norfolk sandy loam [J]. Soil and Tillage Research, 1999, 50(2): 127–135. DOI: https://doi.org/ 10.1016/S0167-1987(98)00199-8.

[10] SHOOP S, COUTERMARSH B A, DIEMAND D, WAY T. Using soil stress state transducers in freezing ground [C]// Conference on Cold Regions Engineering, 2009: 562-571. DOI: 10.1061/41072(359)55.

[11] LU Zheng, YAO Hai-lin, WU Wan-ping, CHEN Ping. Dynamic stress and deformation of a layered road structure under vehicle traffic loads: Experimental measurements and numerical calculations [J]. Soil Dynamics and Earthquake Engineering, 2012, 39(1): 100–112. DOI: https://doi.org/ 10.1016/j.soildyn.2012.03.002.

[12] GARG N, PECHT F, JIA Q. Subgrade stress measurements under heavy aircraft gear loading at FAA national airport pavement test facility [C]// GeoShanghai International Conference. Shanghai, China. 2010: 484–491. DOI: 10.1061/41104(377)62.

[13] THAKUR J K, HAN J, POKHAREL S K, PARSONS R L. Performance of geocell-reinforced recycled asphalt pavement (RAP) bases over weak subgrade under cyclic plate loading [J]. Geotextiles and Geomembranes, 2012, 35(1): 14–24. DOI: https://doi.org/10.1016/j.geotexmem. 2012.06.004.

[14] EGUCHI T, MURO T. Measurement of compacted soil density in a compaction of thick finishing layer [J]. Journal of Terramechanics, 2007, 44(5): 347–353. DOI: https://doi. org/10.1016/j.jterra.2007.10.001.

[15] SUN Xiao-hui, HAN Jie, KWON J, PARSONS R L, WAYNE M. Radial stresses and resilient deformations of geogrid-stabilized unpaved roads under cyclic plate loading tests [J]. Geotextiles and Geomembranes, 2015, 43(5): 440–449. DOI: https://doi.org/ 10.1016/j.geotexmem.2015. 04.018.

[16] TAFRESHI S N M, KHALAJ O, DAWSON A R. Repeated loading of soil containing granulated rubber and multiple geocell layers [J]. Geotextiles and Geomembranes, 2014, 42(1): 25–38. DOI: https://doi.org/10.1016/j.geotexmem. 2013.12.003

[17] ABDELKRIM M, BONNET G, BUHAN P. A computational procedure for predicting the long term residual settlement of a platform induced by repeated traffic loading [J]. Computers and Geotechnics, 2003, 30(6): 463–476. DOI: https://doi.org/ 10.1016/S0266-352X(03)00010-7.

[18] ALAKUKKU L, WEISSKOPF P, CHAMEN W C T, TIJINK F G J, LINDEN J P, PIRES S, SOMMER C, SPOOR G. Prevention strategies for field traffic-induced subsoil compaction: A review: Part 1. Machine/soil interactions [J]. Soil and Tillage Research, 2003, 73(1, 2): 145–160. DOI: https://doi.org/10.1016/S0167-1987(03)00107-7.

[19] WITHERS P J, BHADESHIA H K D H. Residual stress. Part 1–Measurement techniques [J]. Materials Science and Technology, 2001, 17(4): 355–365. DOI: https://doi.org/ 10.1179/030716979803276480.

[20] WITHERS P J, BHADESHIA H K D H. Residual stress. Part 2–Nature and origins [J]. Materials Science and Technology, 2001, 17(4): 366–375. DOI: 10.1179/026708301101510087.

[21] MICHALOWSKI R L, NADUKURU S S. Static fatigue, time effects, and delayed increase in penetration resistance after dynamic compaction of sands [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(5): 564–574. DOI: 10.1061/(ASCE)GT.1943-5606. 0000611.

[22] HAWLADER B C, MUHUNTHAN B, IMAI G. Viscosity effects on one-dimensional consolidation of clay [J]. International Journal of Geomechanics, 2003, 3(1): 99–110. DOI: 10.1061/(ASCE)1532-3641(2003)3:1(99).

[23] MARKGRAF W, HORN R, PETH S. An approach to rheometry in soil mechanics—Structural changes in bentonite, clayey and silty soils [J]. Soil and Tillage Research, 2006, 91(1, 2): 1–14. DOI: https://doi.org/ 10.1016/j.still.2006.01.007.

[24] PISAN. F, JEREMI B. Simulating stiffness degradation and damping in soils via a simple visco-elastic-plastic model [J]. Soil Dynamics and Earthquake Engineering, 2014, 63(1): 98–109. DOI: https://doi.org/10.1016/j.soildyn.2014.02.014.

[25] YIN Jian-hua. Fundamental issues of elastic viscoplastic modeling of the time-dependent stress–strain behavior of geomaterials [J]. International Journal of Geomechanics, 2015, 15(5): A4015002. DOI: https://doi.org/10.1061/ (ASCE)GM.1943-5622.0000485.

[26] DONG Qiao, HUANG Bao-shan. Laboratory evaluation on resilient modulus and rate dependencies of rap used as unbound base material [J]. Journal of Materials in Civil Engineering, 2014, 26(2): 379–383. DOI: https://doi.org/ 10.1061/(ASCE)MT.1943-5533.0000820.

[27] WANG Nian-xiang, ZHANG Wei-min, GU Xing-wen, ZENG You-jin. Model test on inundation swelling deformation of expansive soil foundation [J]. Journal of Highway and Transportation Research and Development 2008, 3(2): 72–76. DOI: 10.1061/JHTRCQ.0000248.

[28] RABOTNOV Y N. Equilibrium of an elastic medium with after-effect [J]. Fractional Calculus and Applied Analysis, 2014, 17(3): 684–696. DOI: https://doi.org/10.2478/s13540- 014-0193-1.

[29] QIAN, Jian-gui, WANG Yong-gang, YIN Zhen-yu, HUANG Mao-song. Experimental identification of plastic shakedown behavior of saturated clay subjected to traffic loading with principal stress rotation [J]. Engineering Geology, 2016, 214: 29–42. DOI: https://doi.org/10.1016/j.enggeo.2016.09.012.

[30] HU Bo, YANG Sheng-qi, XU Peng. A nonlinear rheological damage model of hard rock [J]. Journal of Central South University, 2018, 25(7): 1665–1677. DOI: https://doi.org/ 10.1007/s11771-018-3858-9.

(Edited by FANG Jing-hua)

中文导读

基于小尺寸蠕变试验的花岗岩残积土循环荷载下的动应力累积模型

摘要：通过一系列的小尺寸蠕变试验，首先研究了预压应力为100 kPa的花岗岩残积土的蠕变行为，从而获得了其在不同应力水平下的三种不同类型的蠕变曲线。基于流变学理论与花岗岩残积土在不同应力水平下的蠕变特性，建立了花岗岩残积土的蠕变理论模型，与此同时，根据小尺寸蠕变试验也获得了模型中相关参数的实测数据。然后，基于已建立的蠕变模型，通过推导得到了花岗岩残积土循环荷载条件下的动应力累积理论模型。该理论模型中存在一个动应力累积的阈值，同时模型显示花岗岩残积土的动应力累积规律在不同的循环荷载条件下是不同的。最后，对花岗岩残积土小尺寸试样在不同循环荷载条件下进行了动应力累积规律的试验研究，并将试验结果与理论计算结果进行对比，从而验证了理论模型的有效性。

关键词：花岗岩残积土；蠕变试验；动应力累积模型

Foundation item: Projects(41572277, 41877229) supported by the National Natural Science Foundation of China; Project(2018B030311066) supported by the Natural Science Foundation of Guangdong Province, China; Project(201607010023) supported by the Science and Technology Program of Guangzhou, China

Received date: 2018-02-05; Accepted date: 2018-08-06

Corresponding author: TANG Lian-sheng, PhD, Professor; Tel: +86-20-84039391; E-mail: eestls@mail.sysu.edu.cn; ORCID: 0000- 0003-3635-7776

Abstract: The creep behaviors of granite residual soil with pre-stress of 100 kPa was investigated by a series of small size creep tests. Three different types of strain curves were obtained at different stress levels. Based on creep characteristics of the granite residual soil under different stress levels, a creep model of the granite residual soil was established by rheological theory, and related parameters of the model were determined according to the experimental data at the same time. Further on, based on the established creep model, a theoretical model of dynamic stress accumulation in the granite residual soil under cyclic loading was deduced. It is found that there is a threshold of dynamic stress accumulation in this theoretical model. The dynamic stress accumulation laws of the granite residual soil are different under different cyclic loading stress. Finally, with the dynamic stress accumulation laws in the small-size samples of granite residual soil under different cycle loading studied and the experimental results comparing with the theoretical results, it verifies the validity of the theoretical model.