
Measurement and analyses of molten Ni-Co alloy density
XIAO Feng(肖 锋)1, K. MUKAI2, FANG Liang(方 亮)3, FU Ya(傅 亚)1, YANG Ren-hui(杨仁辉)1
1. College of Materials Science and Engineering, Chongqing Institute of Technology, Chongqing 400050, China;
2. Satellite Venture Business Laboratory, Kyushu Institute of Technology, Kitakyushu 804-8550, Japan;
3. Department of Applied Physics, Chongqing University, Chongqing 400044, China
Received 12 January 2006; accepted 22 September 2006
Abstract:
With the advent of powerful mathematical modeling techniques for material phenomena, there is renewed interest in reliable data for the density of the Ni-based superalloys. Up to now, there has been few report on the density of molten Ni-Co alloy. In order to obtain more accurate density data for molten Ni-Co alloy, the density of molten Ni-Co alloy was measured with a modified sessile drop method, and the accommodation of different atoms in molten Ni-Co alloy was analyzed. The density of alloy is found to decrease with increasing temperature and Co concentration in the alloy. The molar volume of molten Ni-Co alloy increases with increasing Co concentration. The molar volume of Ni-Co alloy determined shows a positive deviation from the linear molar volume, and the deviation of molar volume from ideal mixing increases with increasing Co concentration over the experimental concentration range.
Key words:
Ni-Co alloy; density; molar volume; modified sessile drop method;
1 Introduction
Ni-based heat-resistant alloys are widely applied in aerospace industry to make critical components such as the blades in gas-turbine engines. Their density in liquid state is very important to investigate the structure of liquid alloy, model shrinkage, transport phenomena and macro-segregation, to study the solidification mode and to simulate the solidification and flow behavior in the casting process of alloys. In order to predict the density of the liquid Ni-based superalloys with an arbitrary composition, which usually contain multi components, such as Ni, Cr, W, Ta, Co, Mo, Al, the partial molar volume of these elements in the Ni-based alloy is necessary. Furthermore, with the advent of powerful mathematical modeling techniques for material phenomena, there is renewed interest in reliable data for the density of the Ni-based superalloys. Up to now, there has been few report on the density or molar volume of molten Ni-Co alloy except for the data of WATANABE et al[1] and DZHEMILEV et al[2]. In our previous work, the densities of molten Ni, Ni-Cr[3-6], Ni-W[7, 8], Ni-Al[9] and Ni-Mo[10] were measured and the partial molar volumes of Ni, Cr and Mo in Ni-based binary alloys were obtained. In order to obtain more accurate density data for molten Ni-Co alloy, in this work, the density of molten Ni-Co alloy was measured with a modified sessile drop method developed by MUKAI et al[11] and YU et al[12], and the accommodation of different atoms in molten Ni-Co alloy was analyzed.
2 Experimental
The principle of the modified sessile drop method is shown in Fig.1. A sample is charged into a horizontal alumina (99.9% Al2O3, mass fraction) crucible (24.00 mm in OD, 14.00 mm in ID, 6.00 mm in depth). When the temperature in the furnace is higher than the liquidus temperature of alloy, a drop with smooth surface is formed above the upper end of the crucible with a volume of V2. V1 is the inner volume of crucible at experimental temperature. The total volume of the sample, V, is the sum of V1 and V2. The sample mass is m. The density, ρ, can be obtained from
ρ=m/V (1)

Fig.1 Principle of modified sessile drop method for measurement of density
The experimental apparatus consisted of a LaCrO3 heating furnace, a gas purifier, an oxygen sensor, a photographic system and a digital system (computer). In order to maintain air-tightness of the reaction chamber, a double tube structure was adopted in the study. The tubes were made of high purity alumina. Both ends of the tubes were sealed with water-cooled stainless steel caps. The temperature was measured with a B-type thermocouple, which was positioned directly under the alumina crucible.
The atmosphere in the alumina tube was replaced by argon passed through a gas purifier and further deoxidized by Mg chip heated at 823 K after evacuation with a rotary pump. The oxygen partial pressure in argon, p(O2), was measured with an oxygen sensor of ZrO2-CaO solid electrolyte. The sample was not oxidized during the experiment because the oxygen partial pressure in argon was lower than 1?10-19 MPa.
The photographs of liquid alloy drop were taken every 0.3 ks after holding at a given temperature for 0.6 ks. The Ni and Co concentrations in the alloys were analyzed using radio-frequency inductively-coupled- plasma(ICP) emission spectrometry and the oxygen concentration in the alloys was obtained using an oxygen analyzer. The uncertainty in the density data in this study is estimated as ±0.75%[4, 6].
3 Results and discussion
3.1 Density of molten Ni-Co alloy
The density of molten Ni-Co alloy measured in this study and the values obtained by WATANABE et al[1] are given in Fig.2. The density of Ni-Co alloys decreases with increasing Co concentration over the investigated Co concentration. This is not in agreement with WATANABE et al’s result. The temperature dependence of the density for molten Ni-Co alloy is found to be linear. STEINBERG[13] proposed that the density data of molten alloy can be represented by
ρ=ρL+k(T – TL) (2)
where ρL stands for density at the liquidus temperature TL, and k, in Mg/(m3?K), is the temperature coefficient
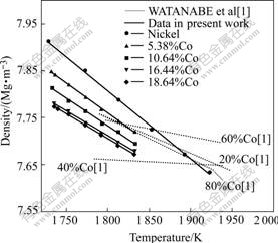
Fig.2 Temperature dependence of density of molten Ni-Co alloy
of density at constant pressure which is expressed as follows:
![]() (3)
(3)
where T is the temperature in Kelvin scale.
If we follow STEINBERG’s formula, the density of molten Ni-Co alloy can be described as follows:
ρ=7.91-1.43×10-3(T-1 728) x(Co)=0
β=1.81×10-4 (4)
ρ=7.86-1.28×10-3(T-1 730) x(Co)=5.38%
β=1.63×10-4 (5)
ρ=7.81-1.17×10-3(T-1 732) x(Co)=10.64%
β=1.50×10-4 (6)
ρ=7.78-1.07×10-3(T-1 734) x(Co)=16.44%
β=1.38×10-4 (7)
ρ=7.77-1.06×10-3(T-1 735) x(Co)=18.64%
β=1.36×10-4 (8)
where b is the thermal expansion coefficient of molten alloy in K-1, and x(Co) the Co concentration in alloy in mole fraction.
The temperature coefficient for the density of molten Ni-Co alloy changes with increasing Co concentration as shown in Fig.3, and is obtained by using the least-square analysis:
k=-1.43×10-3+2.16×10-5x(Co) (9)
As shown in Fig.4, the density decreases with increasing Co concentration in alloy in the temperature range of 1 753-1 833 K. This trend shows a good agreement with WATANABE et al’s result while it is converse with the DZHEMILEV et al’s result, and it can be described as follows.
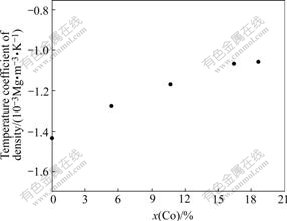
Fig.3 Relationship between temperature coefficient for density of molten Ni-Co alloy and Co concentration
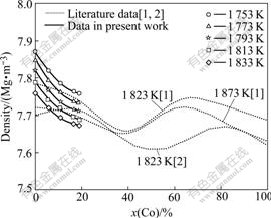
Fig.4 Effect of Co concentration on density of molten Ni-Co alloy
ρ=7.87-1.06×10-2x(Co)+2.49×10-4x(Co)2 (1 753 K) (10)
ρ=7.85-1.09×10-2x(Co)+2.57×10-4x(Co)2 (1 773 K) (11)
ρ=7.82-1.08×10-2x(Co)+2.75×10-4x(Co)2 (1 793 K) (12)
ρ=7.79-0.86×10-2x(Co)+1.87×10-4x(Co)2 (1 813 K) (13)
ρ=7.76-0.85×10-2x(Co)+2.12×10-4x(Co)2 (1 833 K) (14)
Therefore, a least-square analysis of our data gives an equation for the density of molten Ni-Co alloy as a function of temperature and Co concentration as follows:
ρ=(7.91-1.11?10-2x(Co)+1.90?10-4x(Co)2)–(1.43–2.16 ?10-2x(Co))?10-3(T – TL )
(TL≤T≤1 833 K ) (15)
3.2 Coefficient of volume expansion and molar volume for molten Ni-Co alloy
The coefficient of volume expansion is expressed as
![]() (16)
(16)
The coefficient of volume expansion for molten Ni-Co alloy is shown in Fig.5, and it trends to decrease with increasing Co concentration.
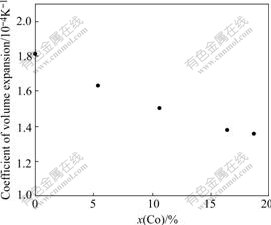
Fig.5 Relationship between coefficient of volume expansion for Ni-Co alloy and Co concentration in alloy
The molar volume of molten Ni-Co alloy can be calculated from the molar mass and the density by the following equation:
![]() (17)
(17)
where Vmol, MNi-Co, and rNi-Co are the molar volume, the molar mass and the density of Ni-Co alloy, respectively. Inserting the values for MNi-Co and rNi-Co for every alloy into Eqn.(17), the molar volume of Ni-Co alloy can be indicated as follows.
![]() (5.38%Co) (18)
(5.38%Co) (18)
![]() (10.64%Co) (19)
(10.64%Co) (19)
![]() (16.64%Co) (20)
(16.64%Co) (20)
![]() (18.64%Co) (21)
(18.64%Co) (21)
The molar volume of Ni-Co alloys is plotted as isothermal molar volumes at different temperatures, in Fig.6, that increases with increasing Co concentration in the alloy. The result in the present work has a same trend as the result obtained by WATANABE et al[1].
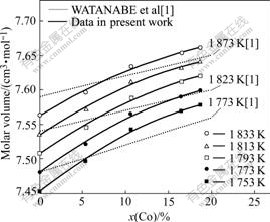
Fig.6 Relationship between molar volume and Co concentration in alloy
In studies of alloys, scientific interest centers on the extent of accommodation among atomic species, expressed as a deviation, DVmix, of the liquid solution from ideal volumetric mixing:
DVmix = Vmol – Videal (22)
where Vmol is the molar volume calculated from the density and Videal the molar volume for ideal mixing.
For Ni-Co alloy
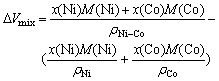 (23)
(23)
where x(Ni) and x(Co) are the molar fractions of Ni and Co, respectively; M(Ni) and M(Co) the molar mass of Ni and Co, respectively, rNi-Co, rNi, and rCo the density of Ni-Co alloy, pure Ni, and pure Co, respectively.
The density of molten Co can be calculated as follows[14]:
ρ=7.75–1.65?10-3(T–1 768) (24)
Fig.7 shows a plot of the molar volume of the Ni-Co alloy at temperatures of 1 773 K and 1 833 K determined in the present work. The dashed lines in the plot represent the ideal mixing of the alloy.
The change of Gibbs free energy G with a change of pressure p at the constant temperature T can be expressed by the following equation[15]:
![]() (25)
(25)
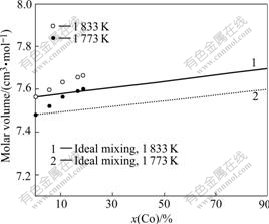
Fig.7 Comparison of measured molar volume with that of ideal mixing
Then, the change of molar volume caused by a mixture of different elements can be determined according to the following relationship:
![]() (26)
(26)
The change of Gibbs free energy DGmix due to the mixture of elements can be calculated as follows:
DGmix=RT[x(Ni)lna(Ni)+x(Co)lna(Co)] (27)
where R is the universal gas constant, a(Ni) and a(Co) are the activities of Ni and Co in the alloy, respectively. From Eqns.(26) and (27), a deduced equation can be gotten:
![]() (28)
(28)
The deviation of molar volume from ideal mixing is shown in Fig.8 together with values obtained by WATANABE et al[1]. The deviation of molar volume from ideal mixing increases with increasing Co concentration over the studied concentration range.
The molar volume of Ni-Co alloys determined in the present work shows a positive deviation from the linear molar volume, which means that Ni and Co mix nonideally. Ni and Co show a positive deviation from Raoults law, and a decrease in pressure at constant temperature will cause a decrease in the activity of Ni and Co. From an elementary viewpoint, it might be presumed that a positive DVmix of Ni-Co alloy means a repulsion or lack of accommodation between Ni and Co atoms.
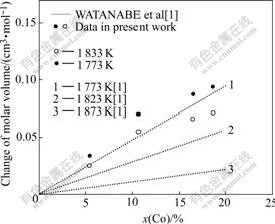
Fig.8 Deviations of molar volume from ideal mixing in Ni-Co alloy
4 Conclusions
1) The density of molten Ni-Co alloys was measured by a modified sessile drop method. The density of molten Ni-Co alloys was found to decrease with increasing temperature and Co concentration.
2) The molar volume of Ni-Co alloys increases with increasing Co concentration.
3) The molar volume of Ni-Co alloys determined in the present work shows a positive deviation from the linear molar volume. The deviation of molar volume from ideal mixing increases with increasing Co concentration over the studied concentration range.
References
[1] WATANABE S, AMATATU M, SAITO T. Densities of Fe-Ni, Co-Ni, Co-Mo and Co-W alloys in liquid state [J]. Transaction of Japan Institute of Metal, 1971, 12(5): 337-342. (in Japanese)
[2] DZHEMILEV N K, POPEL S I, TSAREVSKII B V. Density and surface properties of iron-cobalt-nickel melts at 1 550 ℃ [J]. Russian Journal of Physical Chemistry, 1967, 41(1): 24-27. (in Russian)
[3] XIAO Feng. Density of Ni-Cr alloy in the mushy state [J]. Journal of Materials Science and Technology, 2003, 19(2): 107-110.
[4] XIAO Feng. Density of liquid Ni-Cr alloy [J]. Journal of Materials Science and Technology, 2003, 19(1): 16-18.
[5] MUKAI K, XIAO Feng. Measurement of the density of Ni-Cr alloy by a modified pycnometric method [J]. Materials Transactions, 2004, 45(7): 2357-2363.
[6] MUKAI K, XIAO Feng. Density of Ni-Cr alloy in liquid and solid-liquid coexistence states [J]. Materials Transactions, 2002, 43(5): 1153-1160.
[7] XIAO Feng. Density and structure analysis of molten Ni-W alloys [J]. Journal of Materials Science and Technology, 2004, 20(4): 410-413.
[8] FANG Liang, XIAO Feng. Density of liquid binary Ni-W alloys measured by modified sessile drop method [J]. Rare Metal Materials and Engineering, 2004, 33(12): 1261-1265.
[9] FANG Liang, XIAO Feng. Density of Ni-Al alloys in liquid and solid-liquid coexistence state measured by a modified pycnometric method [J]. Journal of Materials Science and Technology, 2004, 20(4): 405-410.
[10] FANG Liang, MUKAI K, LI Zhu-shu, TAO Zai-nan, XIAO Feng. Density of liquid Ni-Mo alloys measured by a modified sessile drop method [J]. Journal of Materials Science and Technology, 2004, 20(3): 287-292.
[11] MUKAI K, SAKAO H, SANO K. The surface tension and the density of MnO-SiO2-Al2O3 slags as 1 570 ℃ [J]. Journal of Japan Institute of Metals, 1967, 31(9): 928-933. (in Japanese)
[12] YU Zong-da, MUKAI K. Density of molten slag [J]. Journal of Japan Institute of Metals, 1995, 59(3): 806-809. (in Japanese)
[13] STEINBERG D J. A simple relationship between the temperature dependence of the density of liquid metals and their boiling temperature [J]. Metallurgy Transaction A, 1974, 5(8): 1341-1343.
[14] SUNG P K, POIRIER D R, BRIDE E M. Estimating densities of liquid transition-metals and Ni-base superalloys [J]. Materials Science and Engineering A, 1997, 231: 189-197.
[15] SCATCHARD G. Equilibrium in non-electrolyte mixtures[J]. Transaction of Faraday Society, 1937, 99: 160-165.
Foundation item: Project(2000-2005) supported by the New Energy and Industrial Technology Development Organization in Japan; Project(2004527) supported by the Scientific Research Foundation for the Returned Overseas Chinese Scholars; Project(200594) supported by the Chongqing Bureau of Personnel; Project(CSTC2005BA4016-1) supported by the Natural Science Foundation of Chongqing Municipality; Project(2003ZD31) supported by the Chongqing Institute of Technology
Corresponding author: XIAO Feng; Tel: +86-23-66966286; E-mail: xiaofeng@cqit.edu.cn


