J. Cent. South Univ. (2012) 19: 1932-1937
DOI: 10.1007/s11771-012-1228-6![]()
Calculation on inner wall temperature in oil-gas pipe flow
DUAN Ji-miao(段纪淼)1, WANG Wei(王玮)1, ZHANG Yu(张宇)2,
LIU Hui-shu(刘慧姝)1, LIN Ben-qing(林本卿)1, GONG Jing(宫敬) 1
1. Beijing Key Laboratory of Urban Oil and Gas Distribution Technology,
China University of Petroleum (Beijing), Beijing 102249, China;
2. South East Asia Pipeline Company Limited, China National Petroleum Corporation, Beijing 100028, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract:
nbsp;Based on the energy equation of gas-liquid flow in pipeline, the explicit temperature drop formula for gas-liquid steady state calculation was derived. This formula took into consideration the Joule-Thomson effect, impact of terrain undulation and heat transfer with the surroundings along the line. Elimination of temperature iteration loop and integration of the explicit temperature equation, instead of enthalpy energy equation, into the conjugated hydraulic and thermal computation have been found to improve the efficiency of algorithm. Then, the inner wall temperature of gas-liquid flow was calculated by using explicit temperature equation and inner wall convective heat transfer coefficient of mixed flow which can be obtained by liquid convective heat transfer coefficient and gas convective heat transfer coefficient on the basis of liquid holdup. The temperature results of gas-liquid flow and inner wall in the case example presented both agree well with those in professional multiphase computational software OLGA.
Key words:
oil-gas flow; convective heat transfer coefficient; inner wall temperature;
1 Introduction
In recent years, with the vigorous development of oil and gas resources and constant exploitation of waxy crude oil, multiphase transportation technology brings about flow-insurance issues such as wax deposition, hydrate formation and pigging, of which wax deposition is believed to have a significant influence on the security and economical operation of multiphase transportation system. As wax deposition narrows the effective flow area of pipe, delivery capacity reduces, delivery pressure increases and if serious, blockage may occur. All of the thermo-physical parameters of multiphase mixture are connected with the temperature of mixed fluid and the wax deposition rate is relative to the inner wall temperature [1]. Therefore, it is necessary to do some researches on the temperatures of gas-liquid flow and inner wall, which is crucial to security and economical operation of the pipeline system [2].
As the fluid flows in pipe, heat is constantly transferred to the surroundings and temperatures of the fluid and enthalpy value are changed. The temperature drop calculation for gas-liquid flow differs from that for single-phase liquid or gas in that not only the gas-liquid mixture transfers heat to the surroundings through wall, but the mass and heat exchanges between gas and liquid should also be considered. The calculation should take into consideration the Joule-Thomson effect caused by gas cubic expansion and temperature rise as a result of heat generated by friction in liquid flow. Although an accurate prediction of the inner wall temperature distribution of gas-liquid flow is very complicated, the temperature of the mixed fluid can be calculated using the energy equation, that is, enthalpy equation combined with continuity equation and equation of momentum [3].
2 Temperature drop model for gas-liquid flow
In order to simplify the complexity of gas-liquid piping system, some assumptions as to the gas-liquid flow are made as follows: 1) The cross sectional area of pipe is constant; 2) Mixed flow in pipe is regarded as one-dimensional steady flow and the temperature, pressure and other parameters of the mixed fluid are treated as the averages of pipeline section; 3) Heat conduction of the mixed fluid is neglected compared with convective heat transfer of inner wall; 4) Acceleration-induced energy loss is neglected.
When gas-liquid fluids flow through the pipe and the surrounding temperature is colder than the fluids, heat will be lost from the fluids, leading to a decline in temperature. The temperature variation is relative to potential changes, kinetic energy changes and Joule-Thomson effect. We take segment i as the object to study (see Fig. 1).

Fig.1 Enthalpy balance of pipe section i
In stable flow, we assume that gas and liquid flow with identical flow rates. Then, energy equation of gas-liquid mixture can be expressed as

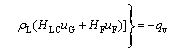
where
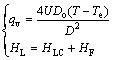
When the gas-liquid flow is under a certain condition of high pressure and low flow rates, acceleration-induced energy loss is neglected. With the assumption, the following expression is proposed:
![]() (3)
(3)
Substituting Eq. (3) into Eq. (1), Eq. (1) can be rewritten as
![]() (4)
(4)
where
![]() (5)
(5)
![]() (6)
(6)
Equation (4) and energy equation of single gas flow are formally consistent. It can be seen that the slipping between gas phase and liquid phase has little impact on the thermal equilibrium of gas-liquid flow and enthalpy value calculation of the mixture if gas-liquid flow is steady and the influence of velocity change on energy equation is neglected.
Specific heat at constant pressure and coefficient of Joule-Thomson effect can be defined as
 (7)
(7)
where cp,m and Di both have functional relationship with enthalpy, pressure and temperature of the gas-liquid mixture. Under the condition that the composition of mixed fluid is constant, hm is given as a function of pressure and temperature by hm=hm(p, T). Therefore,
![]() (8)
(8)
Substituting Eq. (8) into Eq. (4) and combining relationship among thermo-dynamical parameters, we can obtain
![]() (9)
(9)
where a is relaxation distance and defined as a=Wmcp,m/UπDo.
The parameters U, cp,m, Di, Te and dp/dx are assumed to be constant. With the assumption, Eq. (9) can be integrated as
![]()
![]() (10)
(10)
where i and Δxi are the node and length of infinitesimal section, respectively. θ is the angle contained by the infinitesimal section and horizontal level. This model is called manifest temperature drop calculation method (MTDC).
GREGORYHE and AZIZ [4] proposed a simple relationship between enthalpy of gas-liquid mixture and liquid holdup [4], only to find that the effect of liquid holdup on enthalpy of the mixture is insignificant. According to the previous derivation, it is inappropriate to calculate enthalpy of the mixture on the basis of liquid holdup. Instead, it should be calculated by use of mass liquid holdup of the cross section.
CAWKWELL and CHARLES [5] added latent heat of phase change to the calculation of enthalpy increment in energy equation, but methods for calculating latent heat of phase change are not stated [5]. In fact, there is no need to additionally compute the latent heat of phase change, because the phase change between gas and liquid is a gradual process and is included in enthalpy difference between the two phases.
A model was proposed that was applied to calculating the temperature drop of single phase fluid and gas-liquid fluids with a full range of contained angles and unified Coulter-Bardon formula and Ramey formula [6-8]. The mass transfer between gas and liquid was neglected but the pressure gradient, slope of the pipeline, acceleration energy loss, and Joule-Thomson effect in temperature calculation were taken into account and a new method was applied to adjusting specific heat capacity and Joule-Thomson effect coefficient. This model is widely used to calculate temperatures of pipe fluids and is true for both compositional model and black-oil model.
DUKHOVNAYA and ADEWUMI [9] suggested a novel approach in calculating the temperature of gas-liquid flow. In their model, energy equation of gas-liquid mixed fluid doesn’t include kinetic energy term and the potential energy term. One of the main disadvantages of their model is that they neglect the difference between internal energy and enthalpy. MOSHFEGHIAN et al [10] used energy equation that doesn’t contain potential energy term to calculate the temperature of mixed fluid in undulant pipelines. In practice, gas is of high density under high pressure condition, so the effect of undulation, or potential energy, on the temperature drop of mixed fluid should not be ignored. The liquid holdup in gas-liquid pipe affects significantly temperature drop computation, and is dependent on pipeline inclination. For declined pipes, the liquid holdup is relatively low and temperature drop of gas-liquid mixed fluid increases, while for upward pipes, the liquid holdup is high and temperature drop decreases.
LI et al [11-12] derived the method for calculating temperature drop of gas-liquid flow in a horizontal pipe, to directly calculate the temperature drop of two-phase flow in an undulant pipe, by replacing mass gas content with section gas content to calculate specific heat of mixed fluid, and they thought it would obtain a higher precision on calculating temperature of mixed fluid in comparison with the former method. However, based on the former derivation, slipping between gas and liquid has little influence on enthalpy of mixed fluid if kinetic energy is neglected. Therefore, using section gas content in replace of mass gas content for determination of specific heat to calculate the temperature drop in an undulant pipe is seemingly not well-grounded. The feasibility utilizing temperature drop formula, without consideration of the potential energy, to calculate the temperature drop of gas-liquid flow in an undulant pipe is questionable. Furthermore, the temperature drop formula considering Joule-Thomson effect of gas and heat generated by friction of liquid, respectively, is non-uniform in theory. Because Joule-Thomson effect coefficient of oil is below zero and that of gas is over zero within a certain range, oil is heated and gas is cooled due to friction. The friction-generated heat for oil and the Joule-Thomson effect of gas can be uniformly expressed by Joule-Thomson effect of the mixed fluid [13-14].
3 Weighted average convective heat transfer coefficient
The inner wall temperature of gas-liquid flow is mainly dependent on the mixed fluid temperature and the inner wall convective heat transfer coefficient. After determining the temperature of the mixed gas-liquid fluid, the inner wall temperature can be obtained by combining Newton’s law of cooling and energy conservation equation:
![]() (11)
(11)
The latest survey on multiphase heat transfer shows that the open theoretical research on the inner wall convective heat transfer coefficient of multiphase pipe is currently insufficient. There are some empirical correlations on the inner wall convective heat transfer coefficient, most of which, however, are modified based on the single phase flow.
The physical properties of the mixed fluid are closely relative to liquid holdup, so the calculation formula for the inner wall convective heat transfer coefficient presented in this work takes the liquid holdup into account. The mixed fluid is treated as single-phase flow and convective heat transfer coefficient by use of liquid holdup as weighting factor, liquid convective heat transfer coefficient and gas convective heat transfer coefficient are obtained. This is the so-called weighted average of the convective heat transfer coefficient (WACHT). The WACHT is expressed as
![]() (12)
(12)
The inner wall convective heat transfer coefficient is dependent on the thermal-physical properties and flow state of liquid and gas fluids.
In this work, the Dittus-Boelter correlation is used for calculating the inner wall convective heat transfer coefficient of gas phase [15]. For convective heat transfer coefficient of liquid phase, see Ref. [16].
4 Example analysis and comparisons with OLGA
The gas-liquid flow state is complicated with different flow patterns corresponding to different hydraulic resistances, namely different calculations of frictional pressure drop. The continuity equation, momentum equation, flow pattern transitional criterion, phase state, and physical properties of the gas-liquid fluid applied in the example below are shown in Ref. [17].
Pressure iteration is adopted to coupling hydraulic model and thermal-dynamic model in this work, due to the replacement of enthalpy equation with the explicit equation of the temperature field. Therefore, temperature loop is avoided and algorithm is fast-convergent.
Taking a gas-liquid pipeline of Lufeng 13-2 oilfield as an example, the temperatures of mixed fluid and the inner wall calculated by the method proposed in this work and the professional multiphase computational software OLGA are compared.
It is assumed that the gas-liquid pipeline is 20 km in length and undulant in topography. Table 1 presents the operation parameters. The vertical sectional profile of the pipeline is shown in Fig. 2.
Table 1 Operation parameters

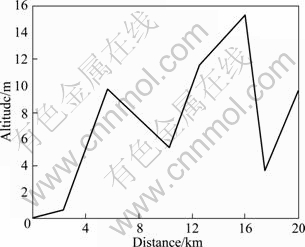
Fig. 2 Vertical sectional profile of pipeline
4.1 Temperature distributions of mixed gas-liquid fluid comparison
The input parameters of MTDC are the same with OLGA in order to draw a comparison between the results. The overall heat transfer coefficient with the outer wall of the pipe as a reference is a constant equal to 3.0 W/(m2·K). Therefore, the calculation for the inner wall convective heat transfer is avoided, that is, the difference of method on the inner wall convective heat transfer has no effect on the temperature of fluid.
Figure 3 and Table 2 show a comparison between temperature distributions along the line calculated with MTDC and OLGA, respectively. In Table 2, the temperature drop refers to the difference of starting point temperature and endpoint temperature. The relative deviation of temperature drop (RETD) is defined as
![]()
It can be seen from Fig. 3 and Table 2 that the prediction of MTDC agrees well with OLGA for gas-liquid flow. In addition to the difference of these two methods, the difference of thermo-physical parameters of the mixed gas-liquid fluid also causes error.
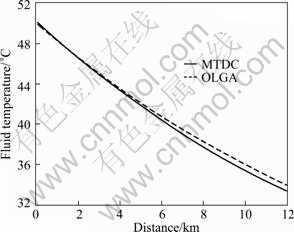
Fig. 3 Comparison of temperature distributions of mixed gas-liquid fluid
Table 2 Result comparison of temperature drop of 20 km-long pipeline

4.2 Inner wall temperature distributions comparison
The WACH is employed to calculate the inner wall convective heat transfer coefficient and thus the overall heat transfer coefficient is obtained. The overall heat transfer coefficient is then substituted into MTDC to calculate the inner wall temperature, which is then compared with that of OLGA. All of the input parameters of MTDC are the same as those of OLGA (see Table 2). Figure 4 and Table 3 show a comparison of inner wall temperature distributions with OLGA.
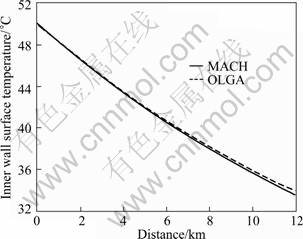
Fig. 4 Comparison of inner wall temperature distributions
Table 3 Results comparison of inner wall temperature of 20 km-long pipeline

It can be seen from Fig. 4 and Table 3 that the inner wall temperature of WACH agrees well with OLGA for gas-liquid flow. The accuracy meets the needs of actual application.
The good agreement between results of the above correlations and OLGA is due to the fact that the convective heat transfer is higher than other heat transfer styles including heat conduction of pipe and insulation layer. The high inner wall convective heat transfer coefficient is responsible for little difference between the temperatures of the mixed fluid and inner wall. The accuracy meets the needs of actual application under appropriate conditions.
5 Conclusions
1) A model named MTDC based on the general energy equation has been introduced to describe the explicit temperature drop formula for gas-liquid steady flow in pipeline. The model, in which the temperature iteration loop is canceled, has accurately predicted the temperature distribution of the mixed fluid. This model has improved the efficiency of algorithm and is applicable to both compositional model and black-oil model.
2) The other model based on the relationship between physical properties of the mixed fluid and liquid holdup is developed for the inner wall convective heat transfer coefficient of gas-liquid flow. The model in conjunction with MTDC has proved to be accurate in predicting the inner wall temperature for gas-liquid flow.
Nomenclature

References
[1] ZHANG Jin-jun, LIU Xin. Some advances in crude oil rheology and its application [J]. Journal of Central South University of Technology, 2008, 15(S1): 288-292.
[2] ZHANG Hong-quan, SARICA, BRILL. Unified model of heat transfer in gas-liquid pipe flow [R]. New York: SPE, 2006.
[3] FENG Shu-chu, GUO Kui-chang. Gathering and field treating of oil and gas [M]. Dongying: China University of Petroleum Press, 2006: 223-259. ( in Chinese)
[4] GREGORY G A, AZIZ K. Calculation of pressure and temperature profiles in multiphase pipelines and simple pipeline networks [J]. Journal of Canadian Petroleum Technology, 1978, 37(5): 56-67.
[5] CAWKWELL M G, CHARLES M E. Pressures, temperatures predicted for two-phase pipelines [J]. Oi1 & Gas Journal, 1985, 83(21): 101-107.
[6] COULTER D M, BARDON M F. Revised equation improves flowing gas temperature prediction [J]. Oi1 & Gas Journal, 1979, 77(9): 107-108.
[7] ALVES I N. ALHANATL F J S, SHOHAM O. Unified model for predicting flowing temperature distribution in wellbores and pipelines [R]. Calgary: SPE, 1992.
[8] RAMEY JR H J.TEXAS A M U. Non-Darcy flow and wellbore storage effects in pressure build up and drawdown of gas wells [J]. Journal of Petroleum Technology, 1965, 24(2): 221-232.
[9] DULCHOVNAYA Y, ADEWUMI A. Simulation of non-isothermal transients in gas-condensate pipelines using TVD scheme [J]. Powder Technology, 2000, 20(3): 163-171.
[10] MOSHFEGHIAN M, JOHANNES A H, MADDOX R N. Thermo-dynamic properties are important in predicting pipeline operations accurately [J]. Oi1 & Gas Journal, 2002, 32(23): 56-62.
[11] YU Xi-chong, FENG Shu-chu, LI Yu-xing. Derive of temperature drop equation of multiphase flown in pipelines [J]. Oil and Gas Storage and Transportation, 2000, 19(4): 22-25. ( in Chinese)
[12] LI Yu-xing, FENG Shu-chu, FAN Chuan-bao. Computation of temperature drop of multiphase flow pipelines [J]. Oil and Gas Storage and Transportation, 2001, 20(9): 32-35. ( in Chinese)
[13] ZHANG Hong-quan, SARICA, BRILL. Unified model for gas-liquid pipe flow via slug dynamics. Part 1: Model development [J]. Energy Res Technol, 2003, 125(4): 266-274.
[14] ZHANG Hong-quan, SARICA, BRILL. Unified model for gas-liquid pipe flow via slug dynamics. Part 2: Model validation [J]. Energy Res Technol, 2003, 125(4): 274-283.
[15] ROSALIND A A, MICHAEL J O. Models for heat transfer from a buried pipe [R]. Calgary: SPE, 1997.`
[16] SHA M M. A general correlation for heat transfer during film condensation inside pipes [J]. Journal of Heat Mass Transfer, 1979, 22(4): 547-556.
[17] XIAO J J, SHPHAM, O, BRILL J P. A comprehensive mechanistic model for two-phase flow in pipelines [R]. Tulsa: SPE, 1990.
(Edited by YANG Bing)
Foundation item: Project(2011ZX05000-026-004) supported by the National Science & Technology Specific Program of China; Project(2010D-5006-0604) supported by the China National Petroleum Corporation (CNPC) Innovation Foundation; Project(51004167) supported by the National Natural Science Foundation of China
Received date: 2011-09-26; Accepted date: 2011-11-14
Corresponding author: GONG Jing, Professor, PhD; Tel: +86-10-89733804; E-mail: ydgj@cup.edu.cn
Abstract: Based on the energy equation of gas-liquid flow in pipeline, the explicit temperature drop formula for gas-liquid steady state calculation was derived. This formula took into consideration the Joule-Thomson effect, impact of terrain undulation and heat transfer with the surroundings along the line. Elimination of temperature iteration loop and integration of the explicit temperature equation, instead of enthalpy energy equation, into the conjugated hydraulic and thermal computation have been found to improve the efficiency of algorithm. Then, the inner wall temperature of gas-liquid flow was calculated by using explicit temperature equation and inner wall convective heat transfer coefficient of mixed flow which can be obtained by liquid convective heat transfer coefficient and gas convective heat transfer coefficient on the basis of liquid holdup. The temperature results of gas-liquid flow and inner wall in the case example presented both agree well with those in professional multiphase computational software OLGA.


