Experimental and numerical investigation on pure aluminum by ECAP
ZHANG Jing(张 静)1, ZHANG Ke-shi(张克实)1, WU Hwai-Chung2, YU Mei-hua(于梅花)1
1. College of Civil and Architectural Engineering, Guangxi University, Nanning 530004, China;
2. Department of Civil and Environmental Engineering, Wayne State University,
Detroit, MI 48202, USA
Received 4 June 2008; accepted 16 June 2009
____________________________________________________________________
Abstract:
The equal channel angular pressing(ECAP) experiments were carried out with industrial pure aluminum and an in-house mould. The comparison of material grain size before and after ECAP was performed by applying the technique of electron back scattered diffraction(EBSD). The results show that the grains in the material after ECAP are refined and the yield stress and ultimate strength are increased. In order to investigate the deformation mechanism during ECAP and the reason for driving grain size refinement, three-dimensional numerical simulations of the ECAP process were carried out. Based on the Lode parameter analysis, the deformation of the material sample is found very complicated, not just pure shear during extrusion through the angular channel. The simulation confirms that a strong strain gradient in the sample material is imposed by the ECAP.
Key words:
pure aluminum; ECAP; grain refinement; strain gradient;
____________________________________________________________________
1 Introduction
The continuum theory assumes material as continuous and uniform. Such an assumption is necessary in many cases. But mechanical behavior of a material is actually dependent on the microstructure of material. So, a more in-depth study on the effects of microstructural discontinuity and heterogeneity on the mechanical behavior of materials were warranted.
In the classical plasticity theory, grain size of metals is regarded to have no influence on their plastic behaviors. But HALL-PETCH relation[1-2] showing increasing yield stress with refinement of grain size was confirmed by many experimental results, meaning that mechanical behavior of a metal may be different if its grain size changes. In order to improve properties of metal, many methods on how grain sizes change were studied. In the 1970s and 1980s, in order to change texture of material, SEGAL[3-5] firstly processed metals by the method of the equal channel angular pressing(ECAP). Later, VALIEV et al[6-7] studied microstructure of material by using this method and found that it would refine grain size of metals; even it was able to obtain nanometer grains. Recently, MAZURINA et al[8] researched the evolutional characteristics of microstructure of material by employing different strain rates during the process of ECAP. HAN et al[9] reported a study on the effect of orientation of grain crystal on the microstructures during the ECAP and put forward a concept that the deformation during the ECAP is mixed form of shearing deformation and bending deformation. REIHANIAN et al[10] considered the effects of low-angular boundary and critical angle of partition grain on flow stress. EHAB and EI-DANAF[11] discussed the relationship between cell structure size and mean micro-orientation angle. ZHILYAEV et al[12] suggested that there is a saturation value of grain refinement during the process of ECAP. KAPOOR and CHAKRAVARTY [13] studied the strain rate sensitivity under different temperatures during the ECAP. ZHANG et al [14-15] researched the evolution of microstructure of steel and saturation value during the process of ECAP. BI et al[16] and WANG etal[17] obtained the sub-micro material by ECAP and discussed the mechanism of grain refinement. ZHANG et al[18-19] completed a comprehensive study on the evolution of microstructure during the process of ECAP and the effect on damping capacity of the material after ECAP.
The ECAP method has the advantages that can alter grain size of material without changes in chemical compositions and without evident changes in shape of material sample[3], which is very appropriate to be used in the investigation of comparison. Therefore, many researchers adopted this method to study the influence of material grain size on material mechanical behavior [8, 10-11, 14, 16, 18]. However, the details of the uneven stress states and deformations in the sample during the ECAP process and their influences on grain size refinement were rarely studied.
In order to study the stress state and deformation mode in the sample during ECAP process, we designed and made the mould in-house, which has an intersecting channel angle of 120?, and its strain imposed in each pass is approximately equal to 0.667[3]. The sample material for this experiment was industrial pure aluminum. For comparison purposes, the mechanical properties of the materials in both the original state and after the ECAP were tested; and their difference in grain size was measured by electron back scatter diffraction(EBSD). The process of the ECAP was simulated by ABAQUS software, and the development of plastic strain and Lode parameter (used to describe the stress state and deformation mode) during the process was predicted from the numerical simulations. On this basis, the effect of deformation mode of the pure aluminum sample during ECAP on grain refinement was able to be investigated further.
2 Experiment with industrial pure aluminum by ECAP
The in-house pressing mould is shown in Fig.1. Its channel has an inner angle of 120? and an outer angle of 60?. This design makes it easy to extrude the sample material through this channel and a large imposed plastic strain in each pass can be obtained. The material of the mould (including plunger and die) was made of the material Cr12. After cutting processing, the mould was treated by quenching to increase its hardness and strength.
Fig.1 Mould of ECAP
The sample material was a cylinder made of industrial pure aluminum, with 9.9 mm in diameter and 80 mm in height. The experiment was performed at room temperature (model of testing machine is YZ-2000A).
After one ECAP pass, all the samples were treated by recrystallization annealing to eliminate internal stresses, which were generated during the process of ECAP, then steady refinement of grain was obtained. The temperature of the recrystallization annealing was 360 ℃ and sample was kept for 30 min before turning off the furnace.
After the thermal treatment, the material in both states original and after ECAP was made into tension specimens by WEDM(wire electrical discharge machine) cutting. Their mechanical properties were tested by material testing machine (AG-IS-MS10kN). And the microstructures of the material were tested by SEM with EBSD (S-3400N). And further, the statistical analysis of the grain size was carried out. The comparison for the material in original state and after ECAP can be performed.
2.1 Influence of ECAP on mechanical properties of material
The changes of yield stress and ultimate strength after extrusion by ECAP (one pass) are shown in Table 1. In the present work, the measurements for stress and strain were respectively Cauchy stress and logarithmic strain; and the yield stress was defined as σ0.2.
From Table 1, the mean yield stresses are 83.95 and 102.63 MPa, respectively, for the material in original state and after ECAP. The improvement of yield stress after ECAP is about 22.25%. And the mean ultimate strengths are 99.05 and 116.68 MPa, respectively, for the material in original state and after ECAP. The improvement is about 17.8%.
Table 1 Comparison for yield stress and ultimate strength of industrial pure aluminum
As a comparison, the nominal stress—strain curves for sample 2 and sample 3 are shown in Fig.2. From Fig.2, one can find that after ECAP treatment, the yield stress and ultimate strength increase obviously. However, the ductility of material decreases. This result should be caused by the refinement of grain size[1-2], and it is changed during ECAP and annealing arranged after ECAP. The refinement of grain size makes the density of grain boundary increase, which raises the obstacle for dislocation movement since dislocation movement across crystal boundary must consume a certain energy. So, if grain boundary density is increased by ECAP, the driving force for dislocation movement over a given length in material would be raised[20]. This result reflects on macro mechanical behavior that presents the rise in yield stress and ultimate strength.
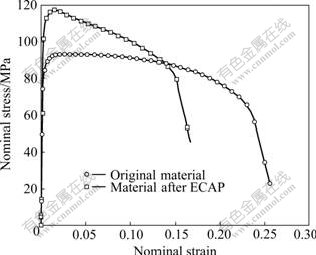
Fig.2 Nominal stress—strain curves in material before and after treatment of ECAP
2.2 Experimental data of EBSD
In order to obtain comparative data of mean grain size for the material before and after ECAP, we adopted the method of EBSD. According to the test, the mean grain size of the pure aluminum in its original state is 62.39 μm and the mean grain size of the material after ECAP is decreased to 40.96 μm. So, the change is about 34.3%, and this means the degree of grain refinement is remarkable.
Fig.3 illustrates a comparison of grain size distribution between the material before and after ECAP. The maximum of crystal grain size is obviously reduced after the ECAP treatment since the maximum grain size in original state is 209.31 μm and that is 106.5 μm after ECAP treatment. The grain size distribution after ECAP is shifted toward 31 μm, its fraction of the crystal grain with size about 31 μm is 48.8% after the ECAP, while it is 33.9% in the original state.
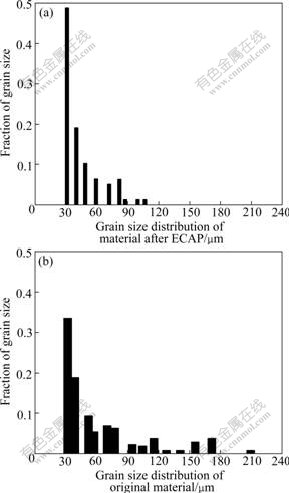
Fig.3 Comparison of grain size distribution between pressed (a) and un-pressed (b) industrial pure aluminum
According to Fig.3, the minimum grain size has not been changed obviously. So, it can be inferred that the effect of ECAP on grain refinement is mainly on the larger crystal grains. The reason for this may be that the strain is much higher for the larger grains when the sample material is extruded through the angular channel of the mould. The larger grains are subjected to more severe shear deformation, leading to higher dislocation density and larger driving force in the larger grains. Hence, a more profound refinement effect on the larger grains is obtained during ECAP.
3 Numerical simulation of ECAP process
3.1 Numerical model
It is difficult to directly measure strain and its distribution in the sample during ECAP process. However, the deformation, strain distribution and stress state in the material during ECAP can be estimated by FEM numerical simulation. In order to simulate the process more close to the real conditions, a three- dimensional model was utilized. And the numerical calculation was executed by applying the software of ABAQUS[21]. It should be pointed out that finite deformation and contact problem are necessary to be taken into account in the numerical ECAP simulation.
The parameters of mechanical properties of the material were determined from experiments (Fig.4). The curve with strain beyond 0.12 is extended as being ideal plastic. Since the deformations of the plunger and the die are very small and they have very little effect on the stress-state of the specimen, both of the plunger and the die are assumed to be rigid body: the plunger is defined as discrete rigid (using element R3D4), while the die is defined as deformable body but it is completely constrained as a rigid body (using element S4R). This treatment can improve computation efficiency very much and almost produces no accuracy loss.
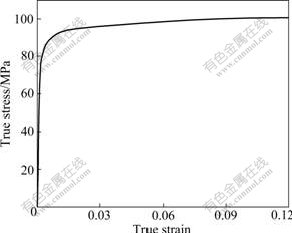
Fig.4 True stress—strain curve of material
The distributions of stress and strain in the material during ECAP are of major interest. The elements must be partitioned fairly small, with individual FE mesh of sample consisting of 8 000 elements (C3D8R) and 9 396 nodes.
Convergence in contact problem calculation is always a challenge in FE simulation. In order to approach the real state, we assumed the contact property as follows: small sliding between the plunger and the sample and finite sliding between the sample and the die. In the simulation, the friction was not taken into account but its main influence is commented. The FE model is shown in Fig.5.
Fig.5 FE model
3.2 Characteristic in different distortional state of sample during ECAP
The deformation process of the sample during ECAP can be analyzed by numerical simulation, and the characteristics at different stages of ECAP can be obtained from the simulation.
During the first stage, the inner side of the sample is separated from the die (the inner side is the side close to inner arc of the die, Fig.6(a)) under pressing by the plunger. At this initial stage, outer side of the sample is constrained by the die to make the sample bend gradually toward the inner side. At the same time, the inner side of the sample continues to move straight down and the contact pressure is lost abruptly, resulting in separation between the inner side of the sample and the die (Fig.6(a)).
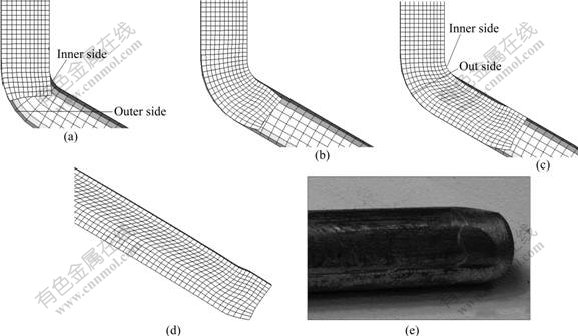
Fig.6 Deformation of sample during ECAP: (a) The first stage; (b) The second stage; (c) The third stage; (d) Deformed state in simulation; (e) Deformed state in experiment
During the second stage, the inner side of sample is bent to conform to the contour of the channel. When the sample is driven downwards by the plunger, the contact pressure from the die is rapidly increased, which forces the specimen bend toward the die. Hence, the inner side of the sample moves gradually to the wall of the die. After the head of sample slides through the angular corner, its underside is separated again from the die, while the inner side is still separated from the die (Fig.6(b)).
During the third stage, the sample material is extruded forward steadily and the inner side of sample is now in contact with the die wall and its underside remains separated from the die (Fig.6(c)).
The various deformation steps described by the numerical simulation for the aluminum sample during ECAP process is found in good agreement with the experiment. Both the inner and the underside of the head of sample appear much smoother, showing strong evidence of being subjected to high pressure (Figs.6(d) and (e)).
3.3 Analysis of Lode parameter
In light of the previous research by SEGAL[3-5], the deformation mode of the sample during ECAP process can be regarded as pure shear, which can be described by the analysis of slip line field using the classical ideal rigid-plastic model under plane strain assumption. For most of elasto-plastic materials, the rigid-plastic sliding model does not provide satisfactory agreements with experiments. Furthermore, the samples used in this study are round in shape so that their deformation is very different from that of 2-D planar samples. So, three-dimension analysis was adopted, the calculation of Lode parameter was performed in the simulation, and the deformation modes of the sample during extrusion by ECAP were analyzed. Lode parameter is shown below:
(σ1≥σ2≥σ3) (1)
where σi is principle stress. According to Eq.(1), the Lode parameter equals zero under pure shear deformation state. Thus, it can be considered the approximate pure shear state if the Lode parameter approximately equals zero. Applying ABAQUS’s user subroutine UMAT, the Lode parameter for the sample material during ECAP can be easily obtained.
In this work, a rectangular coordinate system O-123 was adopted. Section-A is defined by the intersection between coordinate plane O-12 and the sample (Fig.7(a)), and Section-B (Fig.7(b)) is orthogonal to Section-A. The deformations and stress—strain distributions of these sections during ECAP can be analyzed.
Fig.7 Rectangular coordinate system O-123: (a) Section-A; (b) Section-B; (c) Horizontal paths in Section-A
Fig.8 shows the distribution of Lode parameter in the area near the corner in Section-A. One can find that the deformation mode in the middle of the corner zone is approximately pure shear (the white part) and the deformation in most other areas is not pure shear but mixed modes. Also shown in Fig.8, the deformation mode of the inner and outer sides of sample in the corner is not pure shear.
Fig.8 Pure shear area of Section-A
When the sample material enters the corner zone, its outer side is in tension (positive mean stress) and inner side is in compression (negative mean stress). Pure shear only exists in the middle of the corner region. Fairly strong deformation is imposed on the material when it is extruded through the corner zone, especially, the center area subjecting to pure shearing. Under this condition the crystal lattice may be distorted severely. The inhomogeneous deformation can give rise to elastic strain energy stored in the material, and such energy may provide driving force for grain refinement during recrystallization annealing.
3.4 Distribution of equivalent plastic strain in ECAP sample
SEGAL[3] gave a theoretical formula for equivalent plastic strain after treatment of ECAP as below:
(2)
where 
is channel angle. Taking the influence of outer corner into account, IWAHASHI[22] proposed a modified formula with regard to the equivalent plastic strain in the sample after ECAP:
(3)
where φ represents the angle associated with the arc of curvature at which the two parts of the channel intersect. Substituting the inner angle =120? and outer angle φ=60? in Eqs.(2) and (3), we get εp=0.667 and εp=0.604, respectively.
In order to analyze the distribution of the equivalent plastic strain in the sample, we defined 12 equal-spaced paths along the longitudinal direction in sample Section-A. From outer side to inner side the label order is path 1, path 2, …, up to path 12. The sample end that contacted with plunger is defined as the origin of coordinates. The curves of equivalent plastic strain along various paths in the longitudinal direction of sample are shown in Figs.9(a), (b) and (c). The minimum, maximum and average of the equivalent plastic strain at the smooth stage of the curves for different paths are shown in Fig.9(d). The curves shown in Fig.9 are determined at the time when half of the sample just passed the corner of the die.
Fig.9 Distribution curves of 
along lengthwise paths 1-4 (a), 5-8 (b), 9-12 (c), and the max, min and average in all lengthwise paths at steady stage in Section-A (d)
From the distribution curves of equivalent plastic strain during ECAP as shown in Figs.9(a), (b) and (c), 1) equivalent plastic strain is approximately zero before the sample enters the corner zone; 2) equivalent plastic strain increases drastically inside the corner zone; 3) after passing the corner, the equivalent plastic strain enters into a steady stage; 4) when the sample head passes the corner, the imposed plastic strain in the end segment can reach a very high value since the end is constrained strongly and non-uniformly by one side of die wall; 5) meanwhile the other side of sample head has no constraint against the die wall, making the fairly high strain gradient in this head area. Fig.9(d) shows the steady-state equivalent plastic strains for all paths. Longitudinal path 8 has a maximum strain value, 
=0.580, whereas the mean of all the steady-state strain values is 0.468. From Fig.9(d), one can see that the equivalent plastic strains near the center of Section-A are remarkably larger than those near both edges. It is also noted that the plastic strains near the inner edge are higher than those near the outer edge.
In accordance with the revised formula by IWAHASHI et al[22], the theoretical equivalent plastic strain is 0.604 which is close to the mean steady-state value for path 8 by FEM calculation. It is necessary to point out that the average plastic strain for various paths is very different. From these results it can be found that the deformation near the center line of the sample is in good agreement with Eq.(3), and the deformations of other areas may have higher discrepancies than Eq.(3). For example, the difference in average plastic strain between the 4th path and the 8th path is more than 50%.
In order to further understand the distribution of equivalent plastic strain in Section-A, we defined horizontal paths as shown in Fig.7(c), the order from top to bottom is respectively path A, path B, …, path H. The distribution of equivalent plastic strain is shown in Fig.10(a).
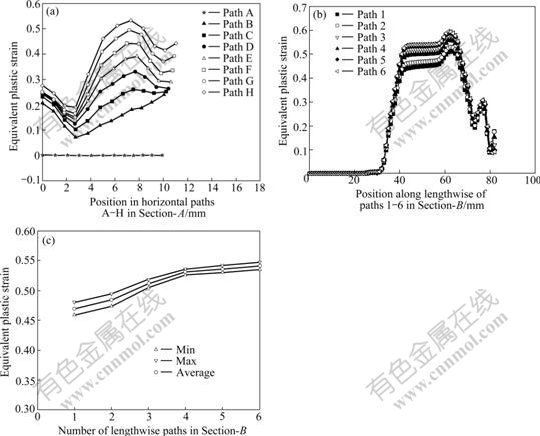
Fig.10 Distribution curves of along horizontal paths defined in Section-A (a), distribution curve of along lengthwise paths 1-6 in Section-B (b), and the max, min and average in all lengthwise paths at steady stage in Section-B (c)
Path H is the first to enter the angular area and then paths G-A take turns to enter during ECAP. Fig.10(a) shows that the equivalent plastic strain for path A is close to zero because the path has not reached the corner, while the equivalent plastic strain for other paths increases evidently and the magnitude of plastic strain is dependent on their order of entering. From Fig.10(a), it is clearly shown that there is a strong accumulated effect on deformation of the materials when they pass the corner zone gradually. One can also see during the process that the accumulated equivalent plastic strain in the middle area is larger than other areas and it is larger in the inner side than in the outer side. That is, the process of specimen crossing the angular zone is not only to create but also to augment the effect of plastic strain.
In Section-B, we defined lengthwise path 1 to path 11, as illustrated in Fig.7(b). Along these paths the distribution of plastic strain are shown in Fig.10(b). From Fig.10(b), it can be found that there is drastic alteration in equivalent plastic strain along all lengthwise paths when the specimen passes through the angular zone in Section-B. The relevant features of plastic strain distribution are similar to Section-A.
From Fig.10(c), it can be shown that the steady-state equivalent plastic strain in lengthwise paths in Section-B is larger in the middle area than near the edge.
3.5 Influence of friction on process of ECAP
The role of friction to the process of ECAP is evaluated by simulation through considering the friction between the contact surfaces of mould channel and the sample. According to the results, the simulated value of the maximal load would be considerably different if the different friction coefficient was applied in simulation; however, the shape of load—displacement curve was very similar. With regarding to the distribution of Lode parameter and plastic strain, the influence of friction is observed mainly on the edge layer of the sample. It should be pointed out that the influence of friction and the determination of friction coefficient are very complicated, which is necessary to investigate further.
4 Conclusions
1) The experimental results indicate that grain size refinement is more profound for larger crystal grains than for smaller grains. Therefore, after ECAP the dispersion degree of grain size of the sample material is decreased.
2) During ECAP, the deformation of sample is non-uniform. The deformation mode in the middle area of the sample is close to pure shear and the remainder areas are not subjected to pure shear.
3) The three-dimensional FE model shows that the distribution of equivalent plastic strain is non-uniform during ECAP and there is severe strain gradient in Section-A. There is a very small area near the center line where the value of equivalent plastic strain is close to that estimated by the IWAHASHI’s formula. The plastic strain near the edge has a remarkable difference with that by the formula.
Acknowledgement
We are grateful to Profs. B. D. WANG, J. X. WEN and J. R. HUANG for their help in carrying out the EBSD experiments.
References
[1] HALL E O. The deformation and ageing of mild steel: III Discussion of results [J]. Proceedings of the Physical Society, 1951, B64: 747-753.
[2] PETCH N J. The cleavage strength of polycrystals [J]. Journal of the Iron and Steel Institute, 1953, 174: 25-28.
[3] SEGAL V M. Materials processing by simple shear [J]. Mater Sci Eng A, 1995, 197: 157-164.
[4] SEGAL V M. Engineering and commercialization of equal channel angular extrusion (ECAE) [J]. Mater Sci Eng A, 2004, 386: 269-276.
[5] SEGAL V M. Equal channel angular extrusion: From macro- mechanics to structure formation [J]. Mater Sci Eng A, 1999, 271: 322-333.
[6] VALIEV R Z, ALEXANDROV I V. Nanostructured materials from severe plastic deformation [J]. Nanostructured Materials, 1999, 12: 35-40.
[7] VALIEV R Z, ISLAMGALIEV R K, SEMENOVA I P. Superplasticity in nanostructured materials: New challenges [J]. Mater Sci Eng A, 2007, 463: 2-7.
[8] MAZURINA I, SAKAI T, MIURA H, SITDIKOV O, KAIBYSHEV R. Effect of deformation temperature on microstructure evolution in aluminum alloy 2219 during hot ECAP [J]. Mater Sci Eng A, 2008, 486: 662-671.
[9] HAN W Z, ZHANG Z F, WU S D, LI S X. Influences of crystallographic orientations on deformation mechanism and grain refinement of Al single crystals subjected to one-pass equal-channel angular pressing [J]. Acta Materialia, 2007, 55: 5889-5900.
[10] REIHANIAN M, EBRAHIMI R, MOSHKSAR M M, TERADA D, TSUJI N. Microstructure quantification and correlation with flow stress of ultrafine grained commercially pure Al fabricated by equal channel angular pressing [J]. Materials Characterization, 2007, 25: 1312-1323.
[11] EI-DANAF E A. Mechanical properties and microstructure evolution of 1050 aluminum severely deformed by ECAP to 16 passes [J]. Mater Sci Eng A, 2007, 487: 189-200.
[12] ZHILYAEV A P, GIMAZOV A A, RAAB G I, LAUGDON T G. Using high-pressure torsion for the cold-consolidation of copper chips produced by machining [J]. Mater Sci Eng A, 2008, 486: 123-126.
[13] KAPOOR R, CHAKRAVARTY J K. Deformation behavior of an ultrafine-grained Al-Mg alloy produced by equal-channel angular pressing [J]. Acta Materialia, 2007, 55: 5408-5418.
[14] ZHANG Zheng, ZHAO Xi-cheng, HUANG Jun-xia. Study of 65 Mn steel by equal channel angular processing [J]. Journal of Xi’an University of Architecture & Technology, 2004, 36(4): 466-469.
[15] ZHANG Zheng, WANG Jing-tao, ZHAO Xi-cheng. Microstructure and grain refinement limit of 7475 aluminum alloy after equal-channel angular pressing [J]. The Chinese Journal of Nonferrous Metals, 2004, 14(5): 741-745. (in Chinese)
[16] BI Jian-qiang, SUN Kang-ning, LIU Rui, FAN Run-hua, WANG Su-mei. Effect of ECAP pass number on mechanical properties of 2A12 Al alloy [J]. Journal of Wuhan University of Technology: Mater Sci, 2008, 23(1): 71-73.
[17] WANG Su-mei, SUN Kang-ning, LIU Rui, BI Jian-qiang. Effect of the second phase on grain refinement of 2A12 aluminum alloy by ECA pressing [J]. Material Science & Technology, 2007, 15(1): 115-117. (in Chinese)
[18] ZHANG Zhong-min, XU Chun-jie, TIAN Jing-lai, WANG Jin-cheng, GUO Xue-feng. Microstructural evolution laws of pure Al L2 during equal channel angular pressing [J]. Journal of Xi’an University of Technology, 2005, 21(3): 227-231. (in Chinese)
[19] ZHANG Z M, XU C J, WANG J C, LIU H Z. Damping behavior of ultrafine-grained pure aluminum L2 and the damping mechanism [J]. Acta Metal Sinica, 2006, 19: 223-227.
[20] HULL D, BACON D J. Introduction to dislocations [M]. DING S S, LI Q. Beijing: Science Press, 1990. (in Chinese)
[21] HIBBIT, KARLSSON & SORENSON. ABAQUS Reference Manuals, V6.5 [M]. 2005.
[22] IWAHASHI Y, WANG J, HORITA Z. Principle of equal channel angular pressing for the processing of ultrafine-grained materials [J]. Scripta Mater, 1996, 35(2): 143-146.
_______________________
Foundation item: Project(10662001) supported by the National Natural Science Foundation of China; Project(0832024) supported by the Natural Science Foundation of Guangxi Province, China; Project(2007105930801M39) supported by Graduate Student Education Innovative Program of Guangxi Province, China
Corresponding author: ZHANG Ke-shi; E-mail: zhangks@gxu.edu.cn
DOI: 10.1016/S1003-6326(08)60442-2
