目录结构

详情信息展示

参考文献

摘要
1液态金属短程有序几何模型的建立
2固态金属X射线衍射峰的宽化
3 讨论▲
参考文献
图▲

图1 理想晶格的X射线衍射峰向纳米畸变晶格宽化峰转变示意图

图2 液态Cu的X射线衍射强度曲线与由固态Cu的 X射线衍射峰宽化而得的强度曲线的比较

图3 液态Al的X射线衍射强度曲线与由BCC固态Al的X射线衍射峰宽化而得的强度曲线的比较

表▲

表1 固态FCC Cu的衍射峰宽化参数

表2 固态FCC Cu的X射线衍射峰的相对强度

表3 固态BCC Al的衍射峰宽化参数

表4 固态BCC Al的X射线衍射峰的相对强度

中国有色金属学报

中国有色金属学报 2004,(06),883-888 DOI:10.19476/j.ysxb.1004.0609.2004.06.001

液态Cu和Al的短程有序结构

田学雷沈军孙剑飞李庆春

哈尔滨工业大学金属精密热加工国防科技重点实验室,哈尔滨工业大学金属精密热加工国防科技重点实验室,哈尔滨工业大学金属精密热加工国防科技重点实验室,哈尔滨工业大学金属精密热加工国防科技重点实验室哈尔滨150001山东大学(南区)材料液态结构及其遗传性教育部重点实验室济南250061 ,哈尔滨150001 ,哈尔滨150001 ,哈尔滨150001

摘要：

为了研究液态Cu和Al的短程有序结构,建立了液态微观结构的纳米晶粒模型。根据这个模型,从晶体X射线衍射学的角度出发,通过对一定晶格结构的固态Cu和Al衍射峰进行宽化处理,计算出了它们的液态X射线衍射强度曲线。结果表明,这些强度曲线与实验获得的液态Cu和Al的X射线衍射强度曲线具有较好的一致性,这不仅证明了纳米晶粒模型的正确性,同时也证明了Cu和Al的液态短程有序结构分别是FCC和BCC。

关键词：

液态金属;微观结构;纳米晶粒模型;短程有序;

中图分类号： TG111

作者简介：田学雷(1963),男,教授,博士.通讯作者:田学雷,教授;电话:05318392727;E mail:tianxuelei@sdu.edu.cn;

收稿日期：2003-09-15

基金：国家自然科学基金资助项目(50395101;50271037);

Structure of short range order in Cu and Al melt

Abstract：

For investigating the structure of short range order(SRO) in Cu and Al melt, a nanocrystalline model for liquid metal was constructed. According to this model, the intensity curves of X-ray diffraction(XRD) of liquid Cu and Al were calculated with broadening XRD peaks of these metals in some crystal structure. The results show that these calculated intensity curves are identical with the results measured with liquid metal X-ray diffractometer on liquid Cu and Al. This fact proves that the nanocrystalline model is correct and that there is a high correlation between the SRO structures of these liquid metals and some crystalline structure, and the SRO structures of Cu and Al melt are FCC and BCC, respectively.

Keyword：

liquid metals; microstructure; nanocrystalline model; short range order;

Received： 2003-09-15

众所周知, 人们对液态结构的认识远不如对固态和气态结构的认识那么清楚。但是, 科学工作者一直在不懈努力地对金属液态结构进行研究。前人为认识金属液态结构建立了各种各样的原子团簇的模型 ^[1] , 如自由体积模型、液体空穴模型、游动原子团簇模型和准多晶模型。这些模型都是以固态的晶格形式为基础, 描述了液态的微观结构。另外, 硬球模型 ^[2,3] 对认识金属液态结构起到了积极的作用。在过去的研究中, 实验研究方法是认识液态金属结构的一个重要手段, 如X射线衍射、中子衍射、 EXASF等研究手段为认识金属液态结构提供了重要的信息。所有这些研究结果都已经证明, 金属液态微观结构是短程有序的。 Cosolapov ^[4] 在比较了Pb和Sn的液态和固态的X射线衍射强度曲线后指出, 液态的Pb和Sn的短程有序结构与其固态的结构相近; Yershov ^[5] 通过对液态Cu的分布函数计算得出液态Cu的最近邻配位数为11.5, 并由此得出液态Cu的短程序结构与其固态的FCC相近。这些研究都说明金属的液态结构与其固态结构具有密切的相关性。对于这种相关性, 目前还没有一个比较合适的物理模型和数学模型对此进行描述。因此, 建立一个物理模型和数学模型对这种液态与固态结构相关性的现象进行描述, 对进一步认识金属的液态结构将起到积极的促进作用。本文作者从晶体几何学的角度出发, 建立了液态金属短程有序的几何模型, 并以Cu和Al为例, 从X射线衍射晶体学的角度证明了这一模型的正确性。

1液态金属短程有序几何模型的建立

随着非晶态合金制备技术的发展, 发现许多非晶合金的偶分布函数的第二峰并不产生分裂 ^[6,7,8] 。通过对非晶态合金的固态、液态分布函数及其配位数和配位球半径的计算分析得知, 其固态与液态具有相近的结构 ^[6] 。这些研究结果支持了这样的观点: 金属的非晶态是金属液态某一时刻状态的保留 ^[9] 。因此, 对金属非晶态的研究将有益于对金属的液态结构的认识, 而机械合金化制备非晶合金的方法 ^{[7,8,10,11,12,13]} 为我们认识金属的液态结构提供了一个很好的途径。

研究者们研究了机械合金化形成非晶的机理后指出 ^[10,14,15] , 在金属机械合金化的过程中, 一方面过饱和溶质造成了晶格的畸变, 另一方面颗粒的尺寸达到一定的临界值(纳米级)时表面原子的晶格发生扭曲, 从而形成了非晶态。另外, 纳米颗粒表面原子晶格的扭曲使这些原子具有很高的能量, 即处于不稳定状态, 这就是非晶态不稳定的原因所在。

对于由机械合金化制备的粉末状非晶来说, 颗粒的直径为10 nm ^[10] 、 40 nm ^[11] 不等。而在过热温度不高时液态共晶合金中存在着不均匀微观区域, 这一不均匀区域的尺度为20 nm ^[16] , 说明液态金属的原子团簇的尺寸是在此数量级上。

由于晶格畸变和晶粒尺寸细小可导致X射线衍射峰宽化, 因此有理由认为机械合金化制备的非晶态合金的X射线衍射峰宽化是由晶体衍射峰经晶格畸变和细小晶粒两种宽化作用叠加而成的。对于固态的金属晶体来说, 其原子有热振动, 而热振动的频率比X射线的慢, 可将热振动看作是一种畸变 ^[17] 。液态金属中的原子同样存在着热振动, 当然也存在着同样的畸变。由于液态金属中原子团簇的表面原子受力不平衡, 且原子团簇的尺寸非常小(10～40 nm), 这会造成因原子团簇内部原子将偏离其平衡位置, 即原子热振动中心发生偏离。因此, 在液态金属中存在着热振动和振动中心偏移造成的畸变, 如同纳米晶粒中的晶格畸变。

综上所述, 可以构造这样一个液态金属短程有序结构的几何模型: 金属的液态是由原子团簇组成的, 这些原子团簇具有某种晶格结构, 但是存在晶格畸变, 而这一畸变类似于由机械合金化制备而得的非晶颗粒中的情况, 即其内部存在着畸变, 而表面具有严重的扭曲——更加严重的畸变。所不同的是, 在液态中一方面原子团簇内部结构的畸变是由原子热振动和振动中心偏移造成的, 即这两种运动的综合作用使每一时刻的原子排列都偏离了正常的晶格点阵; 另一方面由于表面作用的影响, 在原子团簇表面上的原子不仅存在着热运动且受力不平衡, 这使表面原子更加偏离平衡位置、更加不稳定, 随时都在脱离原来的原子团簇, 继而迁移到另外的原子团簇。这使得原子团簇之间的结合力相当脆弱, 导致原子团簇处于此灭彼生的动态平衡, 以至于成为液态金属流动的原因。原子在原子团簇之间的迁移时间非常短, 且占有的空间非常小, 这一空间与原子团簇所占有的空间相比可以忽略不计。因此, 这一模型称为纳米晶粒模型。

2固态金属X射线衍射峰的宽化

2.1固态金属X射线衍射峰宽化的原因

纳米晶粒模型中的原子团簇会对其原有晶格的X射线衍射峰起到宽化作用, 这一宽化作用来自于3部分: 1) 原子团内部畸变的作用; 2) 原子团表面严重畸变的作用; 3) 晶粒细小的作用。

因此, 如果某金属液态原子团簇的晶格结构与某种晶格结构相同, 根据纳米晶粒模型, 则可对这种晶格结构的X射线衍射峰进行宽化处理, 从而得到其液态X射线衍射强度曲线。

2.2固态金属X射线衍射峰宽化公式的推导

现在以Cu为例进行纳米晶粒模型的分析。由于原子团簇的内部和表面都使X射线产生了衍射, 所以总衍射结果是由内部和表面两部分衍射结果合成的。根据纳米晶模型可知, 原子团簇的晶格畸变是不断变化的, 这导致了晶格常数不断变化。晶格常数的变化规律应该是: 在等于正常晶格常数时的概率为最大, 而随着原子团簇的晶格常数与正常晶格常数偏离的增大而减小。因此, 可用正态分布函数:

$f (x) = \frac{1}{\sqrt{π σ}} \exp [- (x - a)^{2} / 2 σ^{2}]$

来描述原子团簇晶格常数的变化规律。由此而造成的正常晶格衍射峰的宽化情况可以用正态分布函数来处理, 且宽化峰下的面积应该等于正常晶格衍射峰的强度。由于原子团簇的内部晶格与表面晶格的畸变程度不一致, 导致了这两部分使正常衍射峰宽化的程度不同。因此, 描述这两部分宽化情况的正态分布函数也是不一样的, 如式(1)所示。

I(2θ)_i=I(2θ)_ii+I(2θ)_io (1)

式中 I(2θ)_i是固态理想晶格的第i个衍射峰宽化后的强度; I(2θ)_ii是原子团簇内部原子的衍射强度; I(2θ)_io是原子团簇外部原子的衍射强度; 且

$\begin{array}{l} Ι (2 θ)_{i i} = Ρ_{1} Ι_{i} \frac{1}{w_{1} \sqrt{2 π}} \exp [- \frac{(2 θ - 2 θ_{i})^{2}}{2 w_{1}^{2}}] ? ? ? (2) \\ Ι (2 θ)_{i o} = Ρ_{2} Ι_{i} \frac{1}{w_{2} \sqrt{2 π}} \exp [- \frac{(2 θ - 2 θ_{i})^{2}}{2 w_{2}^{2}}] ? ? ? (3) \end{array}$

式中 P₁为原子团簇内部原子数的百分数; P₂为原子团簇表面原子数的百分数; 2θ_i为固态理想晶格的第i个衍射峰的衍射角度; I_i为固态理想晶格的第i个衍射峰的强度; w₁为原子团簇内部晶格畸变导致衍射峰宽化的系数; w₂为原子团簇外部晶格畸变导致衍射峰宽化的系数。

由公式(1)、 (2)和(3)得

$\begin{array}{l} Ι (2 θ)_{i} = Ρ_{1} Ι_{i} \frac{\exp [- \frac{(2 θ - 2 θ_{i})^{2}}{2 w_{1}^{2}}]}{w_{1} \sqrt{2 π}} + \\ Ρ_{2} Ι_{i} \frac{\exp [- \frac{(2 θ - 2 θ_{i})^{2}}{2 w_{2}^{2}}]}{w_{2} \sqrt{2 π}} ? ? ? (4) \end{array}$

另外, 晶粒的细小同样可以引起衍射峰的宽化, 且这一宽化对整个衍射峰都将起到衍射作用, 使晶格畸变引起的宽化峰更加宽化。因此, 可以认为晶粒细小的宽化作用体现在使w₁和w₂的增大, 即w₁和w₂可改写为W₁=Cw₁, W₂=Cw₂, 其中C>1, 则式(4)改写为

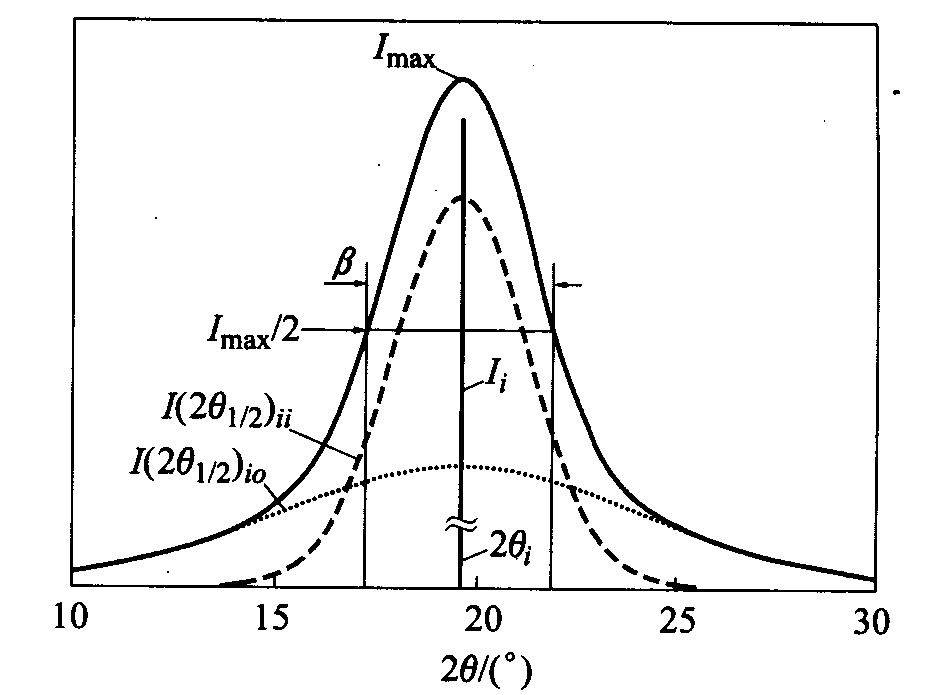
$\begin{array}{l} Ι (2 θ)_{i} = Ρ_{1} Ι_{i} \frac{\exp [- \frac{(2 θ - 2 θ_{i})^{2}}{2 W_{1}^{2}}]}{W_{1} \sqrt{2 π}} + \\ Ρ_{2} Ι_{i} \frac{\exp [- \frac{(2 θ - 2 θ_{i})^{2}}{2 W_{2}^{2}}]}{W_{2} \sqrt{2 π}} ? ? ? (5) \end{array}$

图1所示是式(5)的示意图, 其中2θ_i是I_i的位置; I_max是I(2θ)_i的最大值, 即I(2θ)_i在2θ=2θ_i时的值。由式(5)可得

图1 理想晶格的X射线衍射峰向纳米畸变晶格宽化峰转变示意图

Fig.1 Sketch of XRD peaks from idea crystal structure to aberrant crystal structure

$Ι_{\max} = \frac{Ρ_{1} Ι_{i}}{W_{1} \sqrt{2 π}} + \frac{Ρ_{2} Ι_{i}}{W_{2} \sqrt{2 π}} ? ? ? (6)$

设I(2θ)_i=I_max/2时的衍射角为2θ_1/2, 则由公式(5)和公式(6)得

$\begin{array}{l} Ρ_{1} Ι_{i} \frac{\exp [- \frac{(2 θ_{1 / 2} - 2 θ_{i})^{2}}{2 W_{1}^{2}}]}{W_{1} \sqrt{2 π}} + \\ Ρ_{2} Ι_{i} \frac{\exp [- \frac{(2 θ_{1 / 2} - 2 θ_{i})^{2}}{2 W_{2}^{2}}]}{W_{2} \sqrt{2 π}} = \\ ? \frac{1}{2} (\frac{Ρ_{1} Ι_{i}}{W_{1} \sqrt{2 π}} + \frac{Ρ_{2} Ι_{i}}{W_{2} \sqrt{2 π}}) ? ? ? (7) \end{array}$

由式(7)可知, 一定存在常数K₁、 K₂使

$\begin{array}{l} Ρ_{1} Ι_{i} \frac{\exp [- \frac{(2 θ_{1 / 2} - 2 θ_{i})^{2}}{2 W_{1}^{2}}]}{W_{1} \sqrt{2 π}} = \frac{Κ_{1}}{2} \frac{Ρ_{1} Ι_{i}}{W_{1} \sqrt{2 π}} ? ? ? (8) \\ Ρ_{2} Ι_{i} \frac{\exp [- \frac{(2 θ_{1 / 2} - 2 θ_{i})^{2}}{2 W_{2}^{2}}]}{W_{2} \sqrt{2 π}} = \frac{Κ_{2}}{2} \frac{Ρ_{2} Ι_{i}}{W_{2} \sqrt{2 π}} ? ? ? (9) \end{array}$

成立, 则有

$\frac{Κ_{1}}{2} = \exp [- \frac{(2 θ_{1 / 2} - 2 θ_{i})^{2}}{2 W_{1}^{2}}] ? ? ? (10)$

和

$\frac{Κ_{2}}{2} = \exp [- \frac{(2 θ_{1 / 2} - 2 θ_{i})^{2}}{2 W_{2}^{2}}] ? ? ? (11)$

分别对式(10)和式(11)取自然对数, 并整理得

$W_{1} = \frac{| 2 θ_{1 / 2} - 2 θ_{i} |}{\sqrt{2 (\ln 2 - \ln Κ_{1})}} ? ? ? (12)$

和

$W_{2} = \frac{| 2 θ_{1 / 2} - 2 θ_{i} |}{\sqrt{2 (\ln 2 - \ln Κ_{2})}} ? ? ? (13)$

另外, 由畸变引起的衍射峰的宽度为 ^[18]

β=4ε·tg θ (14)

式中 β是宽化峰I(2θ)_i半高处的宽度, 如图1所示; ε是晶格的相对变形量, 即 $ε = \frac{Δ d}{d}$ , 其中d为晶格常数, Δd为晶格的变形量。在这里ε是原子团簇内部晶格畸变和外部晶格畸变平均值。

式(12)、 (13)中的|2θ_1/2-2θ_i|是衍射强度I(2θ)_i的半高宽的一半, 即: $| 2 θ_{1 / 2} - 2 θ_{i} | = \frac{1}{2} β$ 。所以

|2θ_1/2-2θ_i|=2ε·tg θ (15)

将式(15)代入式(12)和式(13)则得

$W_{1} = \frac{2 ε ? t g θ}{\sqrt{2 (\ln 2 - \ln Κ_{1})}} ? ? ? (16)$

和

$W_{2} = \frac{2 ε ? t g θ}{\sqrt{2 (\ln 2 - \ln Κ_{2})}} ? ? ? (17)$

由式(16)、 (17)可知, 对于一定的试样来说, $\frac{2 ε}{\sqrt{2 (\ln 2 - \ln Κ_{1})}}$ 和 $\frac{2 ε}{\sqrt{2 (\ln 2 - \ln Κ_{2})}}$ 都是常数, 则可令它们分别等于C₁和C₂, 所以

W₁=C₁tg θ (18)

W₂=C₂tg θ (19)

如果固态的理想晶格共有m个衍射峰, 则对每个衍射峰宽化后的结果是

$Ι (2 θ) = \sum_{i = 1}^{m} Ι (2 θ)_{i} ? ? ? (20)$

即

$\begin{array}{l} Ι (2 θ) = \sum_{i = 1}^{m} {Ρ_{1} Ι_{i} \frac{\exp [\frac{(2 θ - 2 θ_{i})^{2}}{2 (C_{1} t g θ)^{2}}]}{C_{1} t g θ \sqrt{2 π}} + \\ Ρ_{2} Ι_{i} \frac{\exp [\frac{(2 θ - 2 θ_{i})^{2}}{2 (C_{2} t g θ)^{2}}]}{C_{2} t g θ \sqrt{2 π}}} ? ? ? (21) \end{array}$

对于固态的晶体来说, 温度升高会引起原子的热振动加剧。这一热振动将使X射线衍射的强度随衍射角的增大而逐渐减小 ^[19,20] , 而背底则是逐渐增高的。强度的减少与因子D²(s)成正比, 而背底的增高则与因子[1-D²(s)]成正比。在这里

D²(s)=exp[-Bs²/2] (22)

式中 B是温度系数, 表示热振动的作用; $s = \frac{2 \sin θ}{λ}$ ; 2θ是衍射角; λ是X射线的波长。令 $s_{i} = \frac{2 \sin θ_{i}}{λ}$ , 其中2θ_i是固态理想晶体第i个衍射峰的位置。

由于实验所得的晶体X射线衍射强度已经存在原子热振动的影响, 而没有考虑背底的影响, 故忽略原子热振动引起的衍射强度降低, 则晶体X射线衍射峰宽化处理公式为

$\begin{array}{l} Ι (2 θ) = \sum_{i = 1}^{m} Ι_{i} {Ρ_{1} \frac{\exp [\frac{(2 θ - 2 θ_{i})^{2}}{2 (C_{1} t g θ)^{2}}]}{C_{1} t g θ \sqrt{2 π}} + \\ Ρ_{2} \frac{\exp [\frac{(2 θ - 2 θ_{i})^{2}}{2 (C_{2} t g θ)^{2}}]}{C_{2} t g θ \sqrt{2 π}}} + \\ A [1 - D^{2} (s)] ? ? ? (23) \end{array}$

由于膨胀的缘故, Cu的液态原子团簇中的原子间距要比固态下的大, 这个现象表现在衍射强度曲线上是峰位向左移动。固态Cu是FCC结构, 假设液态Cu的原子团簇也是FCC结构, 则可以认为晶格常数的增大引起了体积的膨胀。固态Cu的密度是8.92 g/cm³, 由文献 [ 21] 可知1 300 ℃时液态Cu的密度是7.83 g/cm³。由此可以计算出液态Cu的晶格常数平均增加了4.4%。由Bragg方程得液态Cu的衍射角2θ₂与固态Cu的衍射角2θ的关系是

$θ_{2} = \frac{\arcsin θ}{1.044} ? ? ? (24)$

2.3对固态Cu和Al的X射线衍射峰的宽化处理

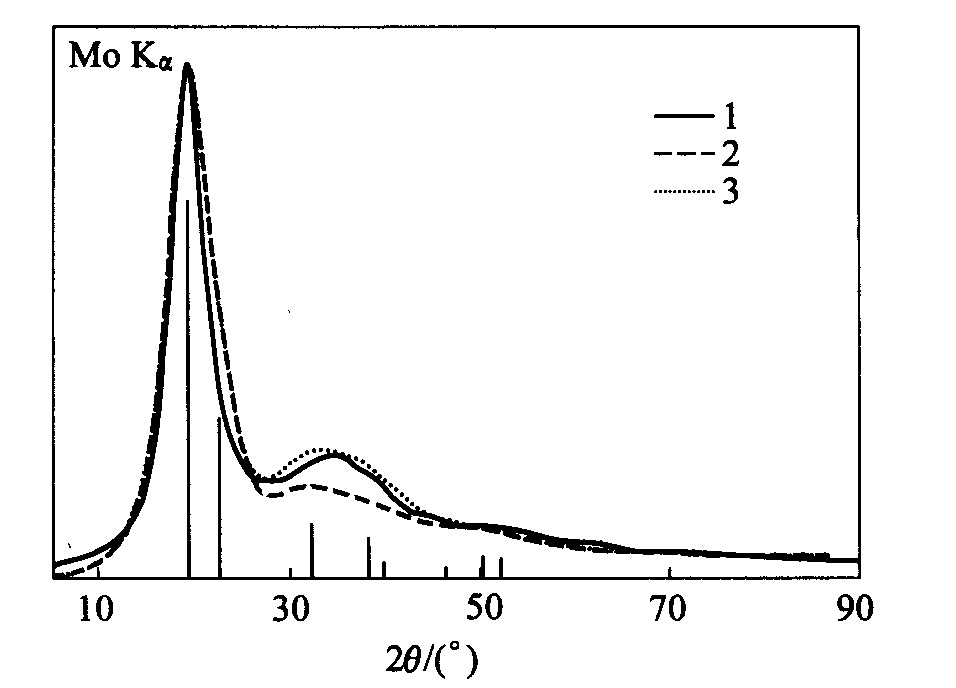
可由式(23)和式(24)对固态Cu的X射线衍射峰进行宽化处理。宽化处理所用的参数和固态Cu的X射线衍射峰的相对强度见表1和表2。图2所示曲线1是1 300 ℃时Cu的液态X射线衍射强度曲线, 曲线2是将FCC固态Cu的X射线衍射峰宽化处理后的曲线, 图2中的竖直线是FCC结构的固态Cu的衍射峰, 曲线3是由文献 [ 17] 中的方法计算出的前5个Cu的固态峰被宽化而得的强度曲线。由图2可以看出, 这3条曲线都能较好地重合在一起。而曲线1和曲线3具有更好的一致性, 说明液态的原子团簇的短程有序结构是FCC。

表1 固态FCC Cu的衍射峰宽化参数

Table 1 Broadening coefficients forsolid FCC Cu XRD peaks

P₁	P₂	C₁	C₂	A	B
0.6	0.4	5	12	0.9	6

表2 固态FCC Cu的X射线衍射峰的相对强度

Table 2 Relative intensity ofXRD peaks of solid FCC Cu

hkl	Peak positions/(°)	Measured I^[22]	Calculated I
111	19.6	100	100
200	22.7	46	47
220	32.3	20	27
311	38.1	17	32
222	39.8	5	9
400	46.3	3
331	50.7	9
420	52.2	8

图2 液态Cu的X射线衍射强度曲线与由固态Cu的 X射线衍射峰宽化而得的强度曲线的比较

Fig.2 XRD intensities of Cu in different states 1—XRD intensity of liquid Cu; 2—Broadening intensity of solid FCC Cu 3—Broadening intensity of calculating on solid FCC Cu; (The vertical lines are XRD peaks of solid Cu, its length is the relative intensity)

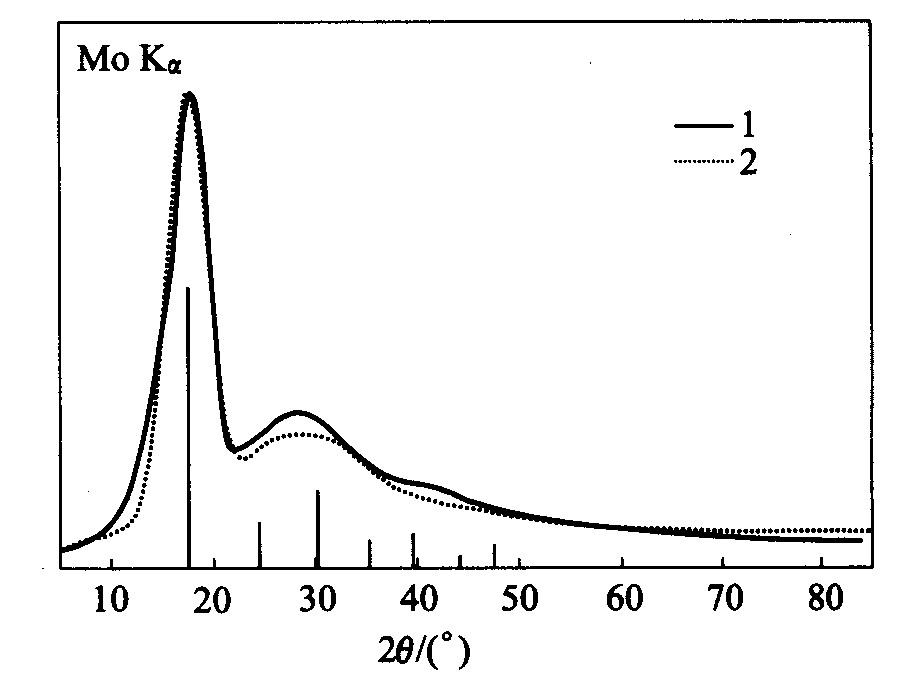
由FCC结构的固态Al的衍射峰宽化而来的衍射强度曲线却不能与Al的液态X衍射强度曲线相一致, 说明Al液态的短程结构不是FCC。假设Al在液态下是BCC结构, 表3和表4列出了BCC固态Al衍射峰宽化处理所用参数和固态衍射峰的相对强度, 并利用由文献 [ 17] 提供的方法计算得到了Al的BCC结构的固态衍射峰。将Al的BCC结构的固态衍射峰宽化得到了与液态Al的衍射强度曲线相一致的曲线。图3给出了按照Al是BCC结构计算出的固态衍射峰、宽化峰和1 250 ℃时Al的液态X射线衍射强度曲线。由图3可以看出, Al的BCC宽化峰与其1 250 ℃时的实验强度曲线非常一致, 说明Al的液态短程结构是BCC。

表3 固态BCC Al的衍射峰宽化参数

Table 3 Broadening coefficients forsolid BCC Al XRD peaks

P₁	P₂	C₁	C₂	A	B
0.8	0.2	6.2	29.2	1.2	12

表4 固态BCC Al的X射线衍射峰的相对强度

Table 4 Relative intensity ofXRD peaks of solid BCC Al

hkl	Peak positions/(°)	Calculated I
110	17.5	100
200	24.8	16.1
211	30.5	29
220	35.4	7.5
310	39.7	8.3
222	43.7	1.6
321	47.4	5.9
400	50.9	0.5

图3 液态Al的X射线衍射强度曲线与由BCC固态Al的X射线衍射峰宽化而得的强度曲线的比较

Fig.3 XRD intensities of Al in different states 1—XRD intensity of liquid Al; 2—Broadening intensity of solid BCC Al (The vertical lines are XRD peaks of BCC Al, its length is the relative intensity)

3 讨论

虽然图2和图3中的实验数据与固态衍射峰的宽化数据较好地重合在一起, 但是, 还有一些差异, 尤其是第二峰以后重合得不是十分理想。造成这些差异的原因主要是由于在假设中的一些忽略造成的: 1) 忽略了液态原子团簇之间的游离原子而造成一定的误差; 2) 背底的处理是用固态晶体中原子热振动情况的公式进行处理的, 而液态中热振动的中心也是在不断变化的, 这一近似也会造成一定的误差; 3) 实验的误差也是造成这些差异的重要因素。

对于Al来说, 在进行固态BCC Al的衍射峰宽化处理过程中, 并没有考虑晶格常数膨胀的影响。其原因在于晶体结构由FCC转变为BCC时, 配位数由12降低为8, 配位数的降低造成了原子间距的减小 ^[23] , 致使原子团簇发生了“收缩”现象。而宏观上Al熔化时发生的膨胀则是由两部分作用叠加造成的, 一是晶格类型由FCC向BCC转变造成的“收缩”; 二是原子团簇之间产生了大量的自由空穴造成的“膨胀”。这种原子团簇“收缩”而自由空穴增加造成宏观膨胀的现象同样存在于In熔体中 ^[24] 。