J. Cent. South Univ. Technol. (2011) 18: 925-931

DOI: 10.1007/s11771-011-0782-7

Statistical evaluation of five failure criteria for intact salt rock

MA Lin-jian(马林建), LIU Xin-yu(刘新宇), FANG Qin(方秦), MA Shu-na(马淑娜)

Engineering Institute of Engineering Crops, PLA University of Science and Technology,

Nanjing 210007, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Key words:

salt rock sequence; bedded rock salt; failure criterion; curve fitting；

1 Introduction

To evaluate salt cavern performance for natural gas storage, an appropriate constitutive model corresponding to a certain failure criterion is needed to accurately characterize the strength and deformation behavior of rock salt under changing pressure conditions. The internal gas pressure on the cavern walls can vary substantially, which may make the stress state of the host salt surrounding the storage cavern change from triaxial compression to triaxial extension, especially in the roof area. Therefore, the chosen failure criterion should be able to account for the lower tensile strength exhibited by rock salt under triaxial extension states of stress as well as for the higher strength under great confining pressures [1]. Most of the previous short-term strength research and long-term cavern stability analysis are based on the Mohr-Coulomb strength theory [2-4], although the linear Mohr-Coulomb criterion tends to overestimate the tensile strength of the salt with a low friction angle. In addition, BRUNO [5] simulated the response of salt at the Permian, Michigan and Appalachian Basins directly with the viscoplastic salt model built in FLAC^3D, which combines the empirical WIPP creep law with the Drucker-Prager criterion. But he didn’t carry out further applicability analysis of the failure criterion. As a matter of fact, each proposed failure criterion is particularly suitable for one rock type or some rock types based on the existing comparative results [6-9]. However, the question which failure criterion and relevant parameters best describe the behavior of the salt rock hasn’t come with an answer  yet.

Therefore, a statistical evaluation of five multiparameter failure criteria: the generalized Hoek-Brown criterion (2002), the Bieniawski empirical criterion (1974), the Sheorey empirical criterion (1989), the Mogi empirical criterion (1967) and the N-type criterion, is presented in this work by comparing them with the strength data from the Brazilian tests, and uniaxial and triaxial compression tests of the salt rock sequence. All the five criteria have the basic form of power law function with an exponent as the envelope shaper whose advantage over the second-order polynomial and linear failure criteria is well recognized. The Levenberg-Marquardt algorithm was utilized to search for the best set of parameters that depict the failure for each criterion and related statistical norms.

2 Five failure criteria

2.1 Generalized Hoek-Brown criterion

To overcome the shortcomings of the original Hoek-Brown failure criterion (1980), HOEK et al [10] proposed a general form of the old one, which can be expressed as

                                      (1)

where σ₁ and σ₃ are the maximum and the minimum effective stresses, σ_ci is the uniaxial compression strength of the intact rock, and m_b is a reduced value of the material constant m_i:

                                           (2)

s and a are constants depending upon the characteristics of the rock mass:

                                                 (3)

                                       (4)

D is a factor which reflects the degree of disturbance of rock masses, varying from 0 for undisturbed in situ rock masses to 1 for severely disturbed rock masses. The geological strength index (I_GS) takes into account of the geometrical shape of the intact rock fragments and the condition of joint faces.

2.2 Bieniawski empirical criterion

BIENIAWSKI suggested an experimental failure criterion for intact rock in 1974, and the relationship between the maximum and the minimum principal stresses [11] can be written as

                                                  (5)

where C₀ is the unconfined compressive strength of intact rock. Parameter α equals 0.75 and b ranges from 3 to 5 according to BIENIAWSKI’s suggestion. The factor a is set to be 1 for the intact salt rock studied here. The Bieniawski criterion was then developed for encompassing the whole range of conditions varying from intact rock to highly jointed rock, which covers the brittle-to-ductile behavior range.

2.3 Sheorey empirical criterion

SHEOREY (1989) attempted to modify the original failure criterion first proposed by BALMER (1952) based on triaxial test data, and the newly improved criterion has the form as

                                                 (6)

Different from other criteria, Sheorey criterion includes both C₀ (uniaxial compressive strength) and σ_t (uniaxial tensile strength), which makes it go through two key strength points (0, C₀) and (-T₀, 0). Furthermore, it is suitable for the analysis of both compression and tension stress areas, which makes the stress analysis complete.

2.4 Mogi empirical criterion (1967)

MOGI conducted precisely confined compression, confined extension and biaxial tests on three different rocks to study the effect of the intermediate principal stress in 1967 [12]. He found out that the influence of the intermediate principal stress on failure is considerably smaller but proportional to the amount of the minor principal stress. Though taking (σ₁+σ₃+ασ₂) as the abscissa instead of (σ₁+σ₃ ) as the independent variable of the maximum shear stress (σ₁-σ₃)/2 or  instead of (σ₁+σ₂+σ₃) as the independent variable of the octahedral shear stress τ_oct, the compression and the extension curves for failure of Westerly granite become coincidental at a suitable value of α. Then, the empirical criterion has the following expression:

                                   (7)

where the constant β is around 0.1 for the brittle rocks and is considerably smaller for the ductile state. The form of function f, which gives the shape of the curve, is dependent on rock type. The term βσ₂ corresponds to the contribution of σ₂ on the fault plane. In this study, we fit the test data using the power law function which was reported in Ref.[13]. The specific formula is

                                 (8)

where k, α and β are curve fitting constants that need to be determined.

2.5 N-type criterion (Generalized Druker-Prager criterion)

N-type criterion is the nonlinear expression of the linear Druker-Prager criterion, where the second invariant of deviatoric stress is replaced by N times power of itself, which is earlier introduced by PARISEAU [14], and has the implicit formula:

                                                 (9)

where I₁=σ₁+σ₂+σ₃, is the first invariant of stress, J₂=[(σ₁-σ₂)²+(σ₂-σ₃)²+(σ₃-σ₁)²]/6, is the second invariant of deviatoric stress, and the exponent N varies from 1 to 2. Alternatively, the inverse form of Eq.(9) is

                                             (10)

Equation (10) may as well be regarded as a specific form of the empirical 1971 Mogi criterion, which is obtained by generalization of the von Mises’s theory and gives satisfactory fitting results to different types of rocks.

3 Experimental data

The specimens in a salt rock sequence obtained from Yincheng deposit (Hubei Province, China) are generally divided into three categories: pure rock salt (halite), bedded composite specimens (anhydrite-halite and mudstone-halite) and interlayers (anhydrite), as shown in Fig.1. Typically, the halite samples consist of 65%-68% NaCl (halite), 4%-6% Na₂SO₄ (sodium sulfate) and 14%-17% CaSO₄ (anhydrite). The insolubles make up around 12% of the total. The mudstone interlayers contain 17%-24% NaCl, 11%-20% Na₂SO₄ and 23%-27% CaSO₄ with the rest of the insoluble part making up to 36%-43%. While the composition of each component in the bedded rock salt is hard to decide because there is a certain amount of either anhydrite or mudstone alternating with halite in the specimens.

Fig.1 Typical rock salt sequence before and after triaxial compression test: (a) Intact salt specimens before experiment; (b) Intact salt specimens after experiment

Pure rock salt from Yincheng deposit is a kind of soft rock which is characterized by remarkably low uniaxial tensile strength (lower than 2 MPa) and uniaxial compressive strength (around 19 MPa) with large ductile deformation under laboratory tests. The elastic modulus of it ranges from 4.4 GPa to 26.6 GPa with a Poisson ratio varying from 0.31 to 0.59 when the confining pressure grows from 0 to 20 MPa. By comparison, the anhydrite interlayers behave in a brittle manner and the corresponding elastic modulus varies from 20.9 GPa to 43 GPa with a strain ratio increasing from 0.2 to 0.43 as the confining pressure reaches 20 MPa. Overall, the lithology of the composite bedded rock salt is somewhat between those of its members (halite and anhydrite), given that its mechanical property depends upon the relative proportion of each component. Ideal full range of strength data sets were collected from the series of tests conducted by the Chinese Academy of Science, Wuhan, for comparative study [15].

4 Comparison of laboratory test data with failure criteria

4.1 Standard statistical norms for comparing criteria [16]

The coefficient of determination R² (COD) is a basic statistic for the measuring the approximation of fit. Note that R² cannot be simply regarded as the square of correlation coefficient, and the exception happens only in the simple linear regression case. The statistic itself is not conceptually prediction-oriented, thus other two statistical norms, the adjusted R² and the residual mean square s², are included in the norm system. They have the definitions:

                              (11)

where σ_1,i is the tested maximum failure stress for data point i,  is the calculated one and  represents the mean value of the observed maximum principal stress. ∑S_Reg and ∑S_Total are the regression sum of squares and the total sum regression. The value of R² ranges from 0 to 1 with 1 for the perfect fitting and 0 for the poor one.

                                        (12)

where ∑S_Res is the residual sum of squares, n is the number of the data set and p is the number of the parameter variable in the criterion model. From the equation, we can see that  overcomes the rise in R², especially when fitting a small sample size (n) by multiple predictor model. Obviously 0≤≤1, similar to R², the upper bound is achieved when the fitting of the criterion to the data is perfect.

                                               (13)

The statistic s² indicates the degree of accuracy of the approximation with the smallest as the best fitting.

The fact that makes evaluation insufficient is researchers are used to choose the best candidate criterion solely by qualifying the fitting without evaluating the quality of future prediction for each fitted criterion which is equally important for comparative study. Then, P_pre statistic, which is in the spirit of data splitting, and the conceptual predictive norm C_p, are especially considered here and have the following expressions:

                                                 (14)

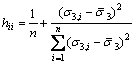                                          (15)

where e_i represents the difference between the observed and the predicted maximum principal stress, σ_3,i is the tested minimum failure stress for data point i, and  is the mean value of the tested minimum principal stress. So one might choose the best failure criterion with the smallest P_pre.

                                        (16)

where δ² is an independent estimate of variance. In the analysis of common practice among data, the residual mean square for the complete criterion model as δ² is used. In this research, the one with the smallest s² is taken as δ². One then favors the candidate criterion with the smallest C_p too.

4.2 Results and discussion

The difficulty of performing multiparameter nonlinear curve-fitting lies in the setting of the initial values of parameters for the employed Levenberg- Marquardt algorithm. Best fitting constants were then achieved by the method of trial and error, instructed by the existing parameters proposed in literatures.

Figures 2-4 show the best fitting results of five failure criteria for three rock types on σ₁-σ₃ plane. Relevant best fitting parameters and calculated statistical norms are summarized in Tables 1-3, respectively.

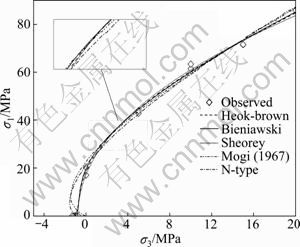
Fig.2 Best-fitting results of five failure criteria for pure rock salt on σ₁-σ₃ plane

Fig.3 Best-fitting results of five failure criteria for anhydrite on σ₁-σ₃ plane

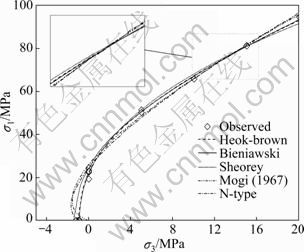
Fig.4 Best-fitting results of five failure criteria for bedded rock salt on σ₁-σ₃ plane

As can be seen in Figs.2-4, all the five empirical criteria are able to account for the low tensile strength with precise estimation of the uniaxial compressive strength of the three soft rocks. Hence, the statistics using five failure criteria consistently achieve high quality values. The R² and the  are consistently larger than 0.975 along with small s² (no more than 33 MPa²); P_pre and C_p demonstrate both good quality of fitness and future prediction of the candidate criteria. The advantage of power function criterion over the other nonlinear criterion (i.e. Hoek-Brown square root parabola) results from more degree of freedom allowed by extra parameters. The best fitting parameters of five criteria yielded for the bedded rock salt are generally in between those for the pure rock salt and the anhydrite interlayers. Moreover, they are much closer to the ones for the pure rock salt than to the other member, which can be ascribed to the resemblance of their lithologies. In the bedded salt specimens, the weaker or more deformable component (halite) is apt to control the total mechanical property. However, the statistics, s² and P_pre, for the anhydrite corresponding to each criterion are roughly 10 times higher than those for the other two rock categories. This could attribute to the scatter of the experimental data caused by material nonhomogeneities and random testing error that is obvious in Fig.3.

Table 1 Best-fitting parameters and statistic values of five failure criteria for pure rock salt (Halite)

Table 2 Best-fitting parameters and statistic values of five failure criteria for anhydrite interlayers

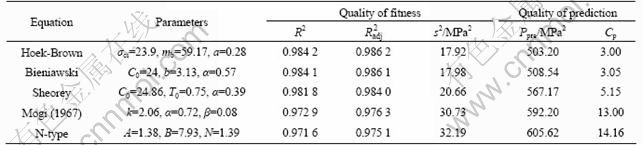
Table 3 Best-fitting parameters and statistic values of five failure criteria for bedded rock salt (anhydrite-halite and mudstone-halite)

As summarized in Tables 1-3, the standard statistics using the two triaxial failure criteria (the generalized Hoek-Brown criterion and the Bieniawski criterion) are within ~15% of each other, and the statistics using the two poly-axial failure criteria are ~30% of each other. The generalized Hoek-Brown criterion is found to work better for two rock strength data sets. The Bueniawski empirical criterion which gives the best fitting to the bedded rock salt and produces nearly the same values of statistics comes the second, with the fitting constant b right in the range of 3-5 as suggested. The Sheorey empirical criterion seems to have an intermediate performance for all the three rock types. In addition, it has an accurate estimation of C₀ and T₀ except for the anhydrite with T₀ of 30% smaller than the measured value. The poly-axial Mogi and the N-type criteria fit the test data equally worse when compared with the other three candidates. The obtained s² using each of them for the measurement of fitness quality is always 1.5 to 2 times larger than that of the others. However, the P_pre and the C_p associated to the measurement of prediction quality are up to 10 times larger than those of the other three failure criteria.

To be more specific, for the halite, the triaxial generalized Hoek-Brown criterion gives the best fitting, closely followed by the Bieniawski triaxial criterion which generates nearly the same statistical norms. The s² and the P_pre obtained using the Sheorey criterion are 35% higher than those using the two former criteria but are ~45% lower than those using the poly-axial Mogi (1967) and N-type criteria. The statistical results (Table 2) for the anhydrite interlayers don’t differ so much compared with others. The values of the s² and the P_pre corresponding to the best fitting (the generalized Hoek-Brown criterion) and the worst fitting (the N-type criterion) differ only by 44% and 19%, respectively.  With respect to the anhydrite-halite composite, the Bieniawski empirical criterion yields the highest R² and  and the lowest s², P_pre and C_p among all the fitted results. The Sheorey criterion gives a good average fitting between the two triaxial and polyaxial failure criteria for the bedded rock salt. For both the halite and the anhydrite-halite composite, the Mogi (1967) is the worst fitting failure criterion, which is quite a contrast to the performance in the case of polyaxial test data [13, 17].

Figures 5-6 present all the results for the Mogi 1967 and the N-type criteria in the (σ₁-σ₃)/2- (σ₁+βσ₂+σ₃)/2 space and the I₁-J₂^1/2 space, respectively. Each strength data set is marked with single symbol with fitted curves on it. Overall, the Mogi (1967) and the N-type empirical failure criteria work well in the strength distribution of all three rocks using monotonically increasing formulae in their own spaces. However, both criteria are found to yield two values of σ₁ for single σ₃ in the low tension zone in the σ₁-σ₃ space, which is physically implausible (Figs.2-4). Similar problem was reported by COLMENARES and ZOBACK when he studied the Mogi (1971) empirical failure criterion in the σ₁-σ₂ space for the Shirahama sandstone and the KTB amphibolite [13]. However, he didn’t take out further theoretical analysis of the issue.

Fig.5 Summary of best-fitting solutions using Mogi empirical criterion (1967) plotted in (σ₁-σ₃)/2-(σ₁+βσ₂+σ₃)/2 space

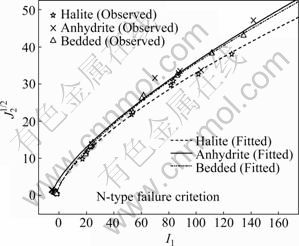
Fig.6 Summary of best-fitting solutions using N-type failure criterion plotted in I₁-J₂^1/2 space

In the case of conventional triaxial test (σ₁>σ₂=σ₃) for the Mogi 1967 criterion, taking the derivative of Eq.(8) with respect to σ₃ yields

                     (17)

At the reflection point, ?σ₁/?σ₃ becomes infinite (Figs.2-4), and it can be obtained that

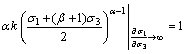                    (18)

By combining Eq.(8) with Eq.(18), the coordinates of the reflection point can be obtained:

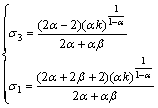                   (19)

At σ₁=0, Eq.(8) gives

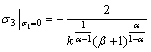                                     (20)

Finally, the interval with the ambiguity problem is got, that is [(2α-2)(αk)^1/(1-α)/(2α+αβ), -2k^1/(1-α)/ (β+1)^α/(1-α)]. Likewise, to ensure the monodromy with respect to the negative area of the σ₃ axis, a limit σ₃=T₀= (2α-2)(αk)^1/(1-α)/(2α+αβ) could be suggested to apply to the Mogi empirical criterion (1967) (Fig.7) if σ₁≤ (2α+2β+2)(αk)^1/(1-α)/(2α+αβ). Similar to the Mogi (1967) criterion, the reflection point for the N-type criterion in the triaxial test case is at (3^(2-N)/(2N-2)(1-N)A^1/(N-1)/  N^N/(N-1)-B/3A, 3^(2-N)/(2N-2)(1+2N)A^1/(N-1)/N^N/(N-1)-B/3A). Then, the corresponding tension cut-off could be made on the boundary of the multivalued interval, as shown in Fig.7.

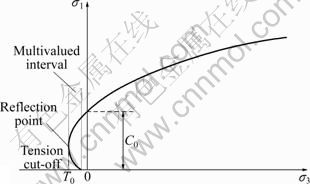
Fig.7 Mogi 1967 or N-type criterion in terms of principal stresses with tension cut-off

5 Conclusions

1) All five chosen criteria are fit for reproducing the strength trend from the tension-low confining region to the high compression region, although the shape of the strength envelop in the tensile zone has never been adequately defined.

2) The parameters corresponding to five criteria for the bedded rock salt are generally closer to those for the pure rock salt than to the pure anhydrite due to the approximation in the lithology.

3) The generalized Hoek-Brown criterion gives the best fittings for both the halite and the anhydrite, followed by the Bieniawski empirical criterion which can obtain the largest R²,  and the smallest s², P_pre and C_p for the bedded rock salt. The Sheorey criterion gets an intermediate performance for all the three rocks.

4) The poly-axial Mogi (1967) and N-type criteria fit the conventional strength data poorer than the three triaxial failure criteria with 1.5-10 times higher s², P_pre and C_p when they ignore the influence of the intermediate principal stress. Eventually, they behave the worst in predicting the strength of three rock types.

5) The ambiguity problem of two poly-axial criteria in the negative area of the σ₃ axis, which is ascribed to the theoretic definition, is suggested to be solved by applying the “tension cut-off” with a limitation at the boundary of the multivalued interval.

References

[1] DEVRIES L K, MELLEGARD D K, CALLAHAN D G, GOODMAN M W. Cavern roof stability for natural gas storage in bedded salt [R]. South Dakota: United States Department of Energy National Energy Technology Laboratory, 2005.

[2] HASEN F D, MELLEGARD K D, SENENV P E. Elasticity and strength of ten natural rock salt [C]// The first Conference on the Mechanical Behavior of Salt. Cleveland: Trans Tech Publ, 1984: 71-83.

[3] SKROTZKI W. An estimate of the Brittle to ductile transition in salt [C]// The first Conference on the Mechanical Behavior of Salt. Cleveland: Trans Tech Publ, 1984: 381-388.

[4] HUNSCHE U. A failure criterion for natural polycrystalline rock salt [C]// Advances in Constitutive Laws for Engineering Materials. Proc ICCLEM (Volume 2). Ottawa: International Academic Publication, 1989: 1043-1046.

[5] BRUNO S M. Geomechanical analysis and design considerations for thin-bedded salt caverns [R]. Arcadia: Terralog Technologies USA, 2005.

[6] PRIEST D S. Determination of shear strength and three-dimensional yield strength for the Hoek-Brown criterion [J]. Rock Mechanics and Rock Engineering, 2005, 38(4): 299-327.

[7] YOU Ming-qing. Ture-triaxial strength criteria for rock [J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46: 115-127.

[8] ALAJMI M A, ZIMMERMAN W R. Relation between the Mogi and the Coulomb failure criteria [J]. International Journal of Rock Mechanics & Mining Sciences, 2005, 42: 431-439.

[9] KUMAR S, PRABIR D, BASUDHAR K. Comparison of intact rock failure criteria using various statistical methods [J]. Acta Geotechnica, 2009, 4: 223-231.

[10] HOEK E, CARRANZA-TORRES C, CORKUM B. Hoek-Brown failure criterion—2002 Edition [C]// Proceedings of the 5th North American Symposium of NARMS-TAC. Toronto: CSM Press, 2002: 31-38.

[11] BIENIAWSKI Z T. Estimating the strength of rock materials [J]. Journal of South Africa Institute of Mine and Metall, 1974, 4(8): 312-320.

[12] MOGI K. Effect of the intermediate principal stress on rock failure [J]. Journal of Geophysical Research, 1967, 72: 5117-5131.

[13] COLMENARES L B, ZOBACK M D. A statistical evaluation of intact rock failure criteria constrained by polyaxial test data for five different rocks [J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39: 695-729.

[14] PARISEAU W G. Fitting failure criteria to laboratory strength tests [J]. International Journal of Rock Mechanics & Mining Sciences, 2007, 44: 637-646.

[15] LIANG Wei-guo, YANG Chun-he, ZHAO Yang-sheng, DUSSEAULT M B, LIU Jiang. Experimental investigation of mechanical properties of bedded salt rock [J]. International Journal of Rock Mechanics & Mining Sciences, 2007, 44: 400-411.

[16] RAYMOND H M. Classical and modern regression with applications [M]. 2nd ed. New York: Tomson Learning, 2005: 164-208.

[17] BENZ T, SCHWAB R. A quantitative comparison of six rock failure criteria [J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45: 1176-1186.

(Edited by PENG Chao-qun)

Foundation item: Project(2009CB724608) supported by the National Basic Research Program of China

Received date: 2010-05-25; Accepted date: 2010-09-14

Corresponding author: MA Lin-jian, PhD candidate; Tel: +86-25-80822027; E-mail: npl.007007@yahoo.com.cn