J. Cent. South Univ. Technol. (2010) 17: 795-800
DOI: 10.1007/s11771-010-0558-5
Rolling force prediction for strip casting using theoretical model and artificial intelligence
CAO Guang-ming(曹光明), LI Cheng-gang(李成刚), ZHOU Guo-ping(周国平),
LIU Zhen-yu(刘振宇), WU Di(吴迪), WANG Guo-dong(王国栋), LIU Xiang-hua(刘相华)
State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110004, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract:
Rolling force for strip casting of 1Cr17 ferritic stainless steel was predicted using theoretical model and artificial intelligence. Solution zone was classified into two parts by kiss point position during casting strip. Navier-Stokes equation in fluid mechanics and stream function were introduced to analyze the
Key words:
1 Introduction
Traditional steel strip production is fundamentally changed by twin roll strip casting, during which the molten liquid steel is cast directly into strip, omitting the processes such as continuous metal casting, re-heating, and hot rolling. It is suitable for the steel industry development tendency of low energy consumption, short procedure, high speed and low production cost. In the past twenty years, aggregate investment for developing strip casting technology is equal to 1%-2% of investment for technology development of steel industry in the world. It can be foreseen that the commercial application of this technique would exert important influence on metallurgical industry and play a revolutionary role in progress of metallurgical industry. This technique is widely applied in fine crystalline and homogenous casting strip of stainless steel and carbon steel [1-3].
Rolling force is an important dynamic parameter that ensures that strip casting proceed steadily, which does not only affect control accuracy for shape and thickness of casting strip, but also affect strip quality. Therefore, it is very important to control rolling force exactly. Deformation procedure during strip casting is considered to be equal during hot rolling, and rolling force for strip casting is calculated by using hot rolling formula and ignoring their differences. In recent years, with deep investigation of rheology characteristic and deformation theory for strip casting, a model for rolling force during casting strip was built, in which static balance differential equation for deformation procedure in casting and rolling zones was deduced by using slab method, and solid phase fraction was introduced to characterize the effect of solid metal on deformation resistance in the model for deformation resistance in casting zone. ZHU et al [4] solved differential equations for casting and rolling zones by using Runge-Kutta method analytically according to friction condition, respectively. The calculation model was built by using non-grid finite element coupling method, and rolling force distribution during rolling was analyzed. Rolling reached the maximum value in the middle of deformation zone and decreased gradually at the entrance and the exit [5]. But there were some limitations during calculation of rolling force by using empirical equation due to the uncertainty of factors such as the kiss point.
In this work, based on analysis of solidification and deformation mechanism in the molten pool, solution zones were devided into two parts by kiss point position during strip casting. The mathematical model of rolling force was established on the basis of viscous fluid mechanics in liquid zone and mushy zone, and the traditional hot rolling model was still used in the solid zone. The differential equation for kiss point position was deduced by using empirical formula, considering geometrical relationship in the molten pool. The kiss point position was acquired by solving differential equation, however, which was very complex. An intelligent algorithm [6] through which the kiss point positions were calculated by using the inversed algorithm according to measured rolling data and the model for the kiss point were proposed by introducing neural networks based on training algorithm of feedforward in Bayesian regularization [7]. There were lots of studies on neural networks based on Bayesian regularization abroad. Neural network was applied to position tracing of users of mobile phone, adopting such standard training methods as anti-propagation algorithm, Elman algorithm and Levenberg-Marquard algorithm in network training, and it was found that network training results by Bayesian regularization were better than those by other methods [8]. Bayesian regularization was firstly applied to the calculation of the kiss point position, and model for rolling force in strip casting was built by combining with other theoretical models mentioned above in this work. Fig.1 shows schematic view of model structure.
2 Rolling force modeling in liquid zone and mushy zone
The inner of the metal underwent a process of liquid phase to solid phase, and the physical characteristic of melted metal in deformation zone was similar to that of viscous fluid although the surface in contact of metal was already solidified in liquid zone and mushy zone. Therefore, Navier-Stokes equation was introduced as the fundamental equation to discuss the rolling force.
(1)
where p represents the hydraulic pressure, Pa; F represents the volume force, N/kg; ρ represents the density, kg/m3; vi represents the speed in direction i, m/s; 
represents the partial derivative of vi and η represents the viscosity coefficient, Pa·s.
Meanwhile, stream function 
was introduced into the velocity filed establishment of the deformation zone, and the analytic equation of average unit compression stress distribution was deduced.
2.1 Basic assumptions
Based on rheological property of casting rolling, some assumptions were given to get the approximate analytic solution.
(1) Deformation in these zones was plane deforma- tion.
(2) Inertia force and volume force were neglectable.
(3) The metal in these zones was viscous and in- compressible fluid.
(4) The metal in these zones was low viscous fluid, and stress-strain relationship was
(2)
where 
represents stress deviator tensor, Pa; and 
represents strain deviator tensor, s-1.
According to the assumptions, the simplified representations of Navier-Stokes equation were
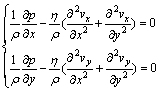(3)
(4)
2.2 Establishment of velocity field
Curvilinear coordinates ξ1 and ξ2 were introduced in the establishment of velocity field, and the deducing process was available in Ref.[9].
(5)
2.3 Velocity boundary conditions
Fig.2 shows schematic view of liquid zone and mushy zone. From Fig.2, thickness hx of any cross section in these zones can be described as
(6)
where hk represents the thickness of kiss point, m; and R
represents the radius of roller, m. The metal fluid stabilized flow was symmetrical to axis x and there were equal interval streamlines, so streamlines could be expressed as a family of curves in the form of Eq.(6). Constant ξ1 of every streamline could be expressed as
(7)
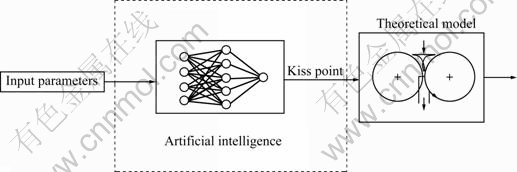
Fig.1 Schematic view of model structure
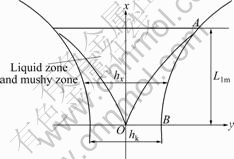
Fig.2 Schematic view of liquid zone and mushy zone
According to the velocity boundary conditions, when x=0, vx=-v0, substituting them to Eqs.(4) and (5) leads to
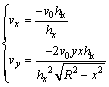(8)
Velocity field was established by Eq.(6), which satisfied both continuous flow function and velocity boundary conditions and was feasible to establish the velocity field using stream function.
2.4 Analytic equation of average unit compression stress distribution
Considering
let 
＝0, substituting it to Eqs.(3) and (8) leads to
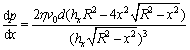(9)
where d represents the thickness of the solidification endpoint, m. In this work, Runge-Kutta algorithm was used for numerically solving Eq.(9).
2.5 Regression model of temperature field
Temperature field calculation was the precondition of rolling force calculation. Much work on flow, heat transfer and solidification in twin-roll strip casting process was done by researchers at home and abroad, and a lot of numerical simulations which exhibited high precision were made [10-12]. The temperature field was unmeasurable and the model calculation needed fast- response ability. Considering the symmetry, coupled turbulent flow and temperature field of the twin-roll casting strip process were simulated by a two-dimensional finite element method. The following time-averaged general formula was given to describe the governing equations in a two-dimensional system of coordinates:
(10)
where CΦ represents the coefficient of instant and convection item; ΓΦ represents the coefficient of diffusion; SΦ represents the heat source; uk represents the momentum in direction k; and 
represents the equation variable.
The temperature field was unmeasurable and the model calculation needed fast-response ability, so on-line application of the finite element method was restrained. In this work, a regression model of temperature (t) was given by using data obtained by finite element simulation.
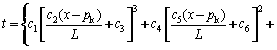
(11)
where tc represents the pouring temperature,℃, and
(12)
L represents the molten level, m, and
(13)
v represents the casting speed, m/s, and
(14)
x represents the present position, m; pk represents the position of kiss point, m; and ci (i=1, 2, …, 22) represents the regression parameter. Fig.3 shows the comparison between temperatures calculated by model and that by Ansys simulation. From Fig.3, it can be seen that the model has high precision.
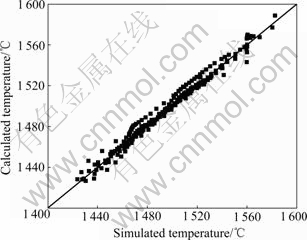
Fig.3 Comparison of calculated temperature with model and simulated one
2.6 Viscosity model
The expression of viscosity of molten metals in liquid zone was:
(15)
where Cgas is the gas constant, J/(mol·K); uA is the viscosity at melt point, Pa·s; C1 is the specific heat capacity of liquid metals, J/(kg·K); T1 is the temperature of liquidus line, K; and T is the temperature of liquid metal, K.
The viscosity in mushy zone can be measured through experiments [13]. The experiment results show that the whole zone could be divided by critical solid fraction and viscosity at solid fraction stages has different varying tendency. The empirical formula was as follows:
(16)
where fs is the solid fraction; fcr is the critical solid fraction; and uA, Ms, k1 and k2 are the empirical formula parameters.
2.7 Solid fraction calculation model
Scheil’s model was used to calculate the solid fraction [14].
(17)
where Ts is the solidus temperature,℃; and k0 is the model parameter.
3 Casting rolling force modeling in solid zone
Because the metal was completely solidified and its deformation process was similar to hot rolling, the traditional hot rolling model was still used.
(18)
where Ps is the casting rolling force in solid zone, N; B is the width of strip, m; 
is the horizontal projection of contact area, m; QP is the influential coefficient; and K is the deformation resistance, Pa.
4 Kiss point calculation model
In order to guarantee high precision of the model, the model parameters must be modified using the measured data and instant message, which was called model self-learning. In the twin-roll strip casting process some variables such as turbulent flow and temperature fields were unmeasured and disturbed by many interacting parameters, so, Bayesian regularization was applied to the training of feedforward neural networks to improve the accuracy of this model.
Bayesian regularization was applied to the training of feedforward neural networks to improve their generalization capabilities. Coupling with the Occam’s razor theory, a penalty item, which could characterize network complexity, was introduced into the performance function to prevent the occurrence of overfitting. The performance function was as follows:
(19)
where ED is the conventional error; 
is the a penalty item of network complexity; wi is the weight; tjk is the expected output; yjk is the actual output; O is the number of output variables; N is the number of training data; G is the number of weight groups; Wg is the number of weight in group g; and αg, β were the hyperparameters.
4.2 Hyperparameters and log evidence (M) calculation
Hyperparameters (αg, β) and M were calculated as follows [15]:
(20)
(21)
(22)
(23)
where H is the Hessian matrix of performance function (19); 
is the number of effective parameters; P is the number of middle layer; ED is the error of prediction; and Ik is the identity matrix.
4.3 Network training procedures
(1) Initialize the hyperparameters (αg, β) and weight of the network using random numbers.
(2) Levenberg-Marquardt equation [16] is applied to the training of feedforward neural networks and updating αg and β.
(3) Calculate performance function and M.
(4) Repeat steps (2) and (3) until the performance function is converged.
4.4 Input of network
The inputs of network contained pouring temperature, roll gap, casting speed, molten level, and cooling water temperature. In this work, the kiss point positions that were calculated by the measured data through the inversed algorithm were used to train the networks. There were 1 000 groups of calculated data, 70% of which were used to train the network and 30% of which were used to verify the network. The experimental material was 1Cr17.
4.5 Network structure selection
Fig.4 shows that there is a redundancy link when the node of middle layer is 2.
The optimal structure of network could be optimized according to the maximization of M and minimization of SEP (the square root of the mean squared error of prediction). Fig.5 shows that with the increase of M, the SEP decreases quickly. Fig.6 is local amplification of Fig.5. When the node of middle layer is 3, the SEP will have centralized distribution and the least forecasting error. So, the optimal structure of network has 3 nodes in the middle layer.
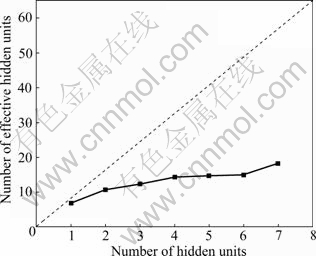
Fig.4 Relationship between number of effective hidden units and number of hidden units
4.6 Network precision
Fig.7 shows the comparison between kiss point position calculated by this network model and that by the inversed algorithm using measured rolling force. It can be observed from Fig.7 that the network model exhibits high precision.
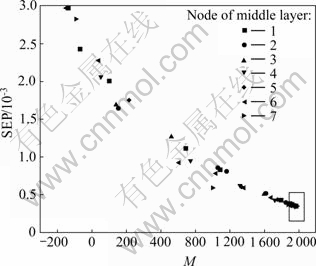
Fig.5 Relationship between square root of mean square error of prediction (SEP) and M
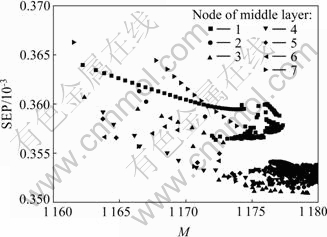
Fig.6 Relationship between square root of mean square error of prediction (SEP) and M
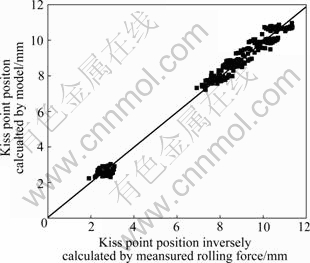
Fig.7 Comparison between kiss point position calculated by model and inversely calculated by measured rolling force
5 Verification of casting rolling force model
The experimental material was 1Cr17. The model parameters are listed in Table 1. From Fig.8, it can be seen that calculation precision of test data of 94.67% is less than ±7.0%, which illustrates that the rolling force model has high precision.
Table 1 Model parameters
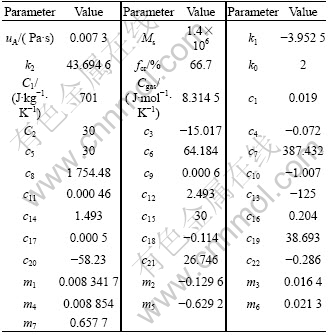
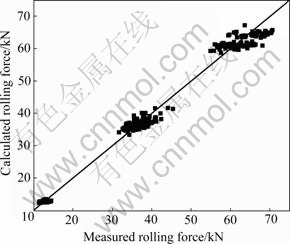
Fig.8 Comparison between calculated and measured rolling forces
6 Conclusions
(1) A model for rolling force prediction is built in which solution zone is divided into two parts by kiss point position during casting strip: liquid zone and mushy zone. Navier-Stokes equation is introduced as the fundamental equation to discuss the rolling force, and the velocity filed is established through stream function. Solid phase fraction, viscosity and temperature distribution model is used, and Bayesian regularization is introduced into the training of feedforward neural networks in calculation of kiss point position.
(2) During rolling force prediction for casting strip of 1Cr17 ferritic stainless steel using this model, calculation precision of test data of 94.67% is less than ±7.0%. This model has high precision for prediction.
References
[1] HAGA T, TKAHASHI K, IKAWAAND M, WATARI H. Twin roll casting of aluminum alloy strips [J]. Journal of Materials Processing Technology, 2004, 153(4): 42-47.
[2] SHIN Y K, KANG T, REYNOLDS T. Development of twin roll strip caster for sheet steels [J]. Ironmaking and Steelmaking, 1995, 22(1): 35-44.
[3] CAVAZOS A, EDWARDS J B. Force/level control of the twin-roller strip caster [J]. Measurement and Control, 2005, 38(9): 276-282.
[4] ZHU Zhi-hua, XIAO Wen-feng, LI Xiao-qian. Modeling of rolling pressure using slab-method and the numerical simulation during twin-roll continuous roll casting process [J]. China Mechanical Engineering, 2002, 13(13): 1091-1094. (in Chinese)
[5] XIONG Gang-yong, TAN Jian-ping, LI Xiao-dong. Calculation of rolling-force distribution of thin gauge roll-casting [J]. The Chinese Journal of Nonferrous Metals, 2005, 15(8): 1243-1247. (in Chinese)
[7] FORESEE F D, HAGAN M T. Gauss-Newton approximation to Bayesian learning [C]// Proceedings of the International Conference on Neural Networks, Houston: IEEE, 1997: 1930-1935.
[8] MIRIKITANI D, NIKOLAEV N. Recursive Bayesian Levenberg- Marquardt training of recurrent neural networks [C]// IEEE International Conference on Neural Networks-Conference Proceedings, Piscataway: IEEE, 2007: 282-287.
[9] SUN Bing-yu, ZHANG Hong, SUN LIN-hang. Theoretical analysis of flow function method in casting-rolling deformation [J]. The Chinese Journal of Nonferrous Metals, 1999, 9(1): 115-117. (in Chinese)
[10] BAE J W, KANG C G, KANG S B. Mathematical model for the twin roll type strip continuous casting of magnesium alloy considering thermal flow phenomena [J]. Journal of Materials Processing Technology, 2007, 191(1/3): 251-255.
[12] JIN Zhu-mei, HE Ji-chen, XU Guang-jie. Numerical simulation of flow, temperature and thermal stress fields during twin-roll casting process [J]. Acta Metallurgica Sinica, 2000, 36(4): 391-394. (in Chinese)
[13] MASAZUMI H, KATSUHIRO T. Effect of chemical composition on apparent viscosity of semisolid alloys [J]. ISIJ International, 1993, 33(11): 1182-1189.
[14] SANTOS C A, SPIM J A, GARCIA J A. Modeling of solidification in twin-roll strip casting [J]. Journal of Materials Processing Technology, 2000, 102(1): 33-39.
[15] AKOUSH S, SAMEH A. Movement prediction using Bayesian learning for neural networks [C]// Second International Conference on Systems and Networks Communications. Cap Esterel: IEEECS, 2006: 30-35.
[16] KIM C T, LEE J J, KIM H. Variable projection method and Levenberg-Marquardt algorithm for neural network training [C]// 2006-32nd Annual Conference on IEEE Industrial Electronics, Piscataway: IEEE, 2006: 4492-4497.
Foundation item: Project(2004CB619108) supported by National Basic Research Program of China
Received date: 2010-04-01; Accepted date: 2010-04-01
Corresponding author: CAO Guang-ming, PhD; Tel: +86-13504187137; E-mail: caogm@ral.neu.edu.cn
(Edited by LIU Hua-sen)
