直齿圆柱齿轮传动设计的全局优化方法
张少军1,万中1,刘光连2
(1. 中南大学 数学与统计学院,湖南 长沙,410083;
2. 中南大学 机电工程学院,湖南 长沙,410083)
摘 要:
动优化设计方法在全局优化方面的不足。针对一类载荷系数一定的直齿圆柱齿轮传动设计的体积优化问题,建立非线性优化模型。基于模型特点的分析,采用变量组合与取自然对数的变量变换方法,将原非线性问题等价地转化为含混合变量的线性规划模型,并设计一类求解混合变量的线性规划问题的全局优化方法。将这一系列方法应用于研究典型的直齿圆柱齿轮传动优化设计案例,并与已有设计优化方法比较。结果表明:该全局优化方法得到的大小齿轮分度圆柱体积小于其他方法得到的圆整最优值。
关键词:
中图分类号:TH122;TH132.41;O221.1 文献标志码:A 文章编号:1672-7207(2013)07-2736-08
Global optimization design of spur gear drive
ZHANG Shaojun1, WAN Zhong1, LIU Guanglian2
(1. School of Mathematics and Statistics, Central South University, Changsha 410083, China;
2. School of Mechanical and Electronic Engineering, Central South University, Changsha 410083, China)
Abstract: The deficiency of global optimization for the current optimal design of gear drive was analyzed. A nonlinear optimization model was constructed to minimize the volume of spur gear drive with a fixed load coefficient. Based on the analysis on the structural characteristics of the model, the original nonlinear optimization problem was converted into a binary linear programming with some continuous and discrete variables by a method of variable transformation. Then,a class of global optimization methods for linear programming with mixed variables were developed. The proposed method was applied into a typical case study on the optimal design of gear drive, and compared with the existent ordinary optimization methods available in the literature. The obtained results show that the optimal total volumes of pinion and wheel by the global optimization method are smaller than the rounded optimal values by the other four local methods.
Key words: gear drive; nonlinear programming; mixed variable; global optimization
齿轮传动是机械传动中最主要的一类传动,形式多样,应用十分广泛。齿轮传动的优化设计旨在节约资源,简化机构,降低成本,改善齿轮工作性能。由于齿轮应用数量巨大,其结构优化无疑能产生较大的经济和社会效益。近年来,已有很多文献对齿轮传动设计优化进行广泛研究。这些文献多以齿轮、变速器总的体积(质量)最小或总的齿轮轴中心距最短作为目标函数[1-2]。也有以承载能力为目标[3]。而随着人们环保意识的增强,以减振降噪等动态性能的改善为目标,已成为齿轮优化研究一个新的焦点,例如文献[4]。此外,还有一些文献从模糊与可靠性优化的角度来设计齿轮传动[5-6]。在齿轮机构优化设计中,应用许多传统优化方法,例如枚举法、复合形法、拟牛顿法、罚函数法等等。枚举法只是一种近似方法,计算效率和精度很低。复合形法、拟牛顿法、罚函数法等属于局部优化算法,虽然其理论与算法都比较成熟,但对于齿轮传动优化这类非凸非线性优化问题往往只能求得局部最优解。近年来,具有一定全局搜索能力的智能启发式算法在齿轮机构优化中的应用越来越多。Faruk等[1]用遗传算法(GA)对直齿轮传动设计进行优化,其结果略优于与之对比的枚举分析法。Savsani等[2]分别采用模拟退火法(SA)和粒子群优化(PSO)算法对一单级直齿轮传动的体积进行优化,并与GA法进行比较,结果显示,SA与PSO优化结果基本一致,均优于GA优化结果,PSO法相比SA和GA法收敛速度更快。Lucian等[7]在一个包含齿轮、轴、轴承、润滑、密封等环节共计24类77个约束的二级斜齿轮减速器的重量优化问题中,设计一种两阶段进化算法来优化该问题。智能启发式算法虽然不依赖梯度信息,具有全局、并行的优化性能,为解决大规模非线性优化问题提供了新的思路和手段[8],但该类方法至今还无法从理论上证明所得到的解一定是全局最优解。已有齿轮传动优化设计的方法不能从理论上保证解的全局最优性。而现有的确定性全局优化算法如分支定界法、填充函数法、积分水平集算法等尽管算法理论严谨,但它们都是针对特殊的优化问题展开的[9]。对一般非凸优化问题,不存在任何一种普遍适用的全局优化算法。齿轮传动应用广泛,其优化模型相对很成熟,研究它的高效确定性全局优化算法,其理论与应用价值都很大。但这需要以深入分析优化模型特点为基础,这恰好是已有研究存在的一个普遍不足。最近,Zhang等[10-11]就V带传动设计优化问题提出基于问题本身结构特征的一种确定性全局优化算法 —— 最优值线段算法。与文献[10-11]的思想类似,本文针对一类直齿圆柱齿轮传动设计优化问题,根据实际设计环境,首先建立该类问题的非线性优化模型,然后基于模型特点,提出合适的变量变换方法,把原非线性问题等价地转化为线性规划问题求解,并针对设计变量的多属性,设计一种含二元混合变量的线性规划问题的全局优化方法。最后,将建立的模型和求解方法应用于一个典型齿轮传动设计实例,并与4种常规优化方法的结果进行比较,以验证其有效性和实用价值。
1 直齿圆柱齿轮传动优化设计模型
1.1 确定设计变量和目标函数
由于在给定的传递功率和传动比条件下,齿轮副体积最小具有重量轻,成本低,结构紧凑等优点,因此,选取大小齿轮分度圆柱体积之和最小为目标函数。选择模数m (mm),主动轮齿数Z1和齿宽系数Φd作为设计变量,记为x = (x1, x2, x3)T=(m, Z1, Φd)T,则目标函数为
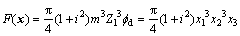 (1)
(1)
其中:i为传动比。
1.2 建立约束条件
约束条件主要包括几何约束和性能约束。
1.2.1 几何约束
(1) 模数的约束:
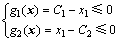 (2)
(2)
(2) 主动轮齿数的约束:
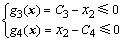 (3)
(3)
(3) 齿宽系数的约束:
 (4)
(4)
其中:C1~C6为约束条件中的常系数。
1.2.2 性能约束
(1) 齿面接触疲劳强度的限制
根据文献[12],有
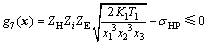 (5)
(5)
其中:ZH为区域系数,对标准直齿圆柱齿轮,ZH=2.5;Zi为齿数比系数,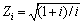 ;ZE为弹性影响系数(
;ZE为弹性影响系数(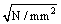 ),对于齿轮常用的锻钢材料,ZE=189.8;T1为主动齿轮传递的扭矩(N·mm);K1为载荷系数;
),对于齿轮常用的锻钢材料,ZE=189.8;T1为主动齿轮传递的扭矩(N·mm);K1为载荷系数; 为许用接触应力(N/mm2),
为许用接触应力(N/mm2),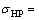
 ,
,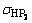 和
和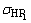 分别为大、小齿轮的许用接触应力(N/mm2)。
分别为大、小齿轮的许用接触应力(N/mm2)。
(2) 齿根弯曲疲劳强度的限制
根据文献[12],有:
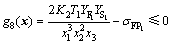 (6)
(6)
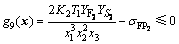 (7)
(7)
其中: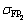 和
和 分别为大、小齿轮的许用弯曲应力(N/mm2);K2为载荷系数;
分别为大、小齿轮的许用弯曲应力(N/mm2);K2为载荷系数;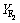 和
和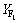 分别为载荷作用于齿顶时大、小齿轮的齿形系数;
分别为载荷作用于齿顶时大、小齿轮的齿形系数;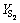 和
和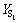 分别为载荷作用于齿顶时大、小齿轮的应力修正系数。根据文献[13],有:
分别为载荷作用于齿顶时大、小齿轮的应力修正系数。根据文献[13],有:
YFYS = 7.377686 Z–0.322 312×1.094062 Z0.116 206=
8.071646 Z–0.206 106;17≤Z≤25
YFYS=4.333869 Z–0.159 188×1.175585 Z0.094 493=
5.0948314 Z–0.064 695;25≤Z≤60
YFYS=2.859508 Z–0.057 395×1.276 Z 0.0738=
3.648732 Z0.016 405;60≤Z≤300
其中:Z表示齿数;YF和YS分别为载荷作用于该齿轮齿顶时的齿形系数和应力修正系数。
在式(5)中,载荷系数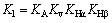 。在式(6)和(7)中,载荷系数
。在式(6)和(7)中,载荷系数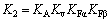 。其中:KA为工作情况系数;Kv为动载系数;
。其中:KA为工作情况系数;Kv为动载系数; 和
和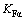 分别为计算接触应力和计算弯曲应力时的齿间载荷分配系数;而
分别为计算接触应力和计算弯曲应力时的齿间载荷分配系数;而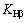 和
和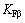 分别为计算接触应力和计算弯曲应力时的齿向载荷分布系数。在这些系数中,KA由齿轮的工作环境状况决定,而Kv,
分别为计算接触应力和计算弯曲应力时的齿向载荷分布系数。在这些系数中,KA由齿轮的工作环境状况决定,而Kv, ,
,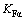 ,
,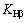 和
和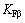 与齿轮的模数、齿数、齿宽以及齿轮转速等参数相关[14]。但对于经齿向修形或者经过仔细跑合,能使载荷沿齿向均匀分布的情形,可取
与齿轮的模数、齿数、齿宽以及齿轮转速等参数相关[14]。但对于经齿向修形或者经过仔细跑合,能使载荷沿齿向均匀分布的情形,可取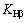 =
=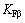 =1。对经过齿廓修形的齿轮,还可取
=1。对经过齿廓修形的齿轮,还可取 =
=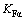 =1[15]。对于高精度齿轮,在良好的安装和对中精度以及合适的润滑条件下,Kv的取值变化范围很小,为1.0~1.1[14]。本文的研究对象即为这类经过齿向和齿廓修形,精度较高的直齿圆柱齿轮传动,其载荷系数K1和K2主要由KA决定,可近似认为K1=K2=K,其中K为一常数。
=1[15]。对于高精度齿轮,在良好的安装和对中精度以及合适的润滑条件下,Kv的取值变化范围很小,为1.0~1.1[14]。本文的研究对象即为这类经过齿向和齿廓修形,精度较高的直齿圆柱齿轮传动,其载荷系数K1和K2主要由KA决定,可近似认为K1=K2=K,其中K为一常数。
同时,该问题还是一混合变量优化问题,即含连续变量、规则和非规则离散变量的优化问题。设x1∈Ω,x2∈Z+,x3∈R+(Ω表示区间[C1, C2]内的标准模数的集合,Z+表示全体正整数集,R+表示正实数集)。
综上所述,直齿圆柱齿轮传动设计问题的优化模型为:
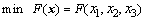
s.t. 式(2)~(7)
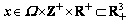 (8)
(8)
其中: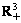 表示三维非负欧几里德空间。
表示三维非负欧几里德空间。
2 变量变换及等价的混合变量线性规划模型
模型(8)是一非线性优化模型,虽然变量不多,但至今并没有一种统一的全局优化方法。典型的高效优化算法,如序列二次规划方法,一般只能保证得到其局部最优解。各种求解实际优化问题的启发式算法,如遗传算法和粒子群算法,虽然有可能得到其全局最优解,但运算量往往较大,且理论上还无法建立其全局收敛性。基于这些考虑,在此提出一种基于问题(8)结构特征的变量变换方法,它能把原来的非线性问题等价地转化为线性问题求解。
首先,令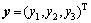 =
=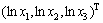 。记
。记 。对目标和各约束函数均取自然对数,则模型(8)等价于如下问题:
。对目标和各约束函数均取自然对数,则模型(8)等价于如下问题:
min W(y)=ln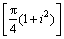 +3y1+3y2+y3
+3y1+3y2+y3
s.t. 3y1+3y2+y3≥A1
3y1+2.206106y2+y3≥A2;17≤x2≤25
3y1+2.064695y2+y3≥A3;25≤x2≤60
3y1+2.064695y2+y3≥A4;25≤ix2≤60
3y1+1.983595y2+y3≥A5;60≤ix2≤300
lnC1≤y1≤lnC2 (9)
lnC3≤y2≤lnC4
lnC5≤y3≤lnC6
yi = lnxi,i = 1, 2, 3
x = (x1, x2, x3)T∈Ω×Z+×R+
其中:
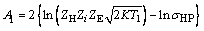 ,
,
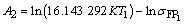 ,
,
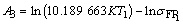 ,
,
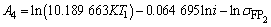 ,
,
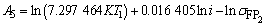 。
。
若不考虑模型(9)中最后2个约束,则所需求解的问题是一个以y为决策变量的线性规划。
注1:任何一种求解线性规划问题的算法都可以用于求解或近似求解问题(8)。典型的简单近似算法如下。
步骤1:选用线性规划问题的求解器求解上述问题(9) (不考虑最后2个约束),记其最优解为y*。
步骤2:由y*计算
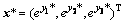
步骤3:将 圆整,即得近似最优设计方案。
圆整,即得近似最优设计方案。
注2:注1中对线性规划问题的连续解圆整的方法是一种粗糙的方法。许多实例表明:该方法所得到的原问题的最优解离实际混合变量全局最优解很远。较理想的方法是设计原混合变量优化问题的全局最优解法。虽然可将连续变量处理成离散变量,进而采用线性整数规划方法来求解该问题[16],不过这类整数规划方法一般只能给出一个全局最优解,不能找到所有最优解,而且求解过程相对复杂。如何能得到此类问题所有全局最优设计方案,至今未见相关研究成果。
3 混合变量线性规划问题的全局优化方法
为设计求解问题(8)的混合变量全局最优解的有效方法,建立以下3个定理。
定理1 设混合变量线性规划的目标函数为
min F(x) = B1x1+B2x2+…+Bnxn
其中:B1, B2, …, Bn为常数。设可行域为Ψ,该线性规划在连续变量空间中的全局最优解为P=(xP 1,xP 2,…,xP n)T,则过点P且与目标函数所代表的超平面簇平行的超平面π可表示为:B1x1+B2x2+…+Bnxn-D=0。其中,D=B1xP 1+B2xP 2+…+BnxP n。设混合变量全局最优解为P*=(xP* 1, xP* 2, …, xP* n)T,则必有点P*与π的距离最近,即
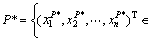
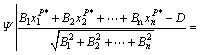
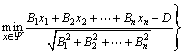 (10)
(10)
证明:式(10)等价于
 。
。
对于一般混合变量线性优化问题的求解较难,但对于二元混合变量线性优化问题,可以通过下面2个定理来求解。
定理2 如图1所示,假设二元混合变量线性规划问题:
min F(V) = B1v1+ B2v2
B1和B2为常数
s.t. V∈Ψ,Ψ为二元混合变量空间中的可行域 (11)
在连续变量空间中的全局最优解为P点,不失一般性,设v1为连续变量,v2为离散变量,记经过点P且与目标函数直线簇平行的直线为π,设靠近直线π一侧的可行域边界线上,分别沿v2坐标的正方向和负方向距离P点最近的混合变量可行解为V(1)=(v1(1),v2(1))和V (2)=(v1(2),v2(2)),则该优化问题的混合变量全局最优解为
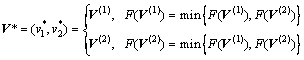
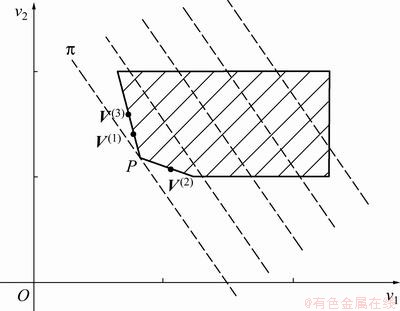
图1 定理2的几何表示
Fig.1 Geometric representation for Theorem 2
证明:由线性规划理论知,点P是组成可行域的凸集的一顶点。不失一般性,设F(V(1))= min{ F(V (1)), F(V(2))}。现利用反证法证明。
假设有一混合变量全局最优解V(3)=(v1(3),v2(3))≠ V(1),则必有:
(a) v2(3)=v2(1),v1(3)≠v1(1);
或(b) v2(3)=v2(2),v1(3)≠v1(2);
或(c) v2(3)>v2(1),或者v2(3)<v2(2)。
若(a)成立,则由图解知,必有点V (3)与π的距离大于点V (1) 与π的距离,说明F(V (3))>F(V (1)),与假设矛盾;
若(b)成立,同理可得F(V (3))>F(V(2))>F(V(1)),与假设矛盾;
若(c)成立,不失一般性,假设v2(3)>v2(1),设直线v2=v2(3)与靠近直线π一侧的可行域边界的交点的横坐标为v1(3)*。若v1(3)≠v1(3)*,则必有
F(v1(3),v2(3))>F(v1(3)*,v2(3))
这与V (3)在混合变量空间中的全局最优性假设相矛盾,因此,v1(3)=v1(3)*。由于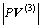 >
>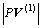 ,其中
,其中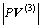 表示点P与点V(3)的距离,所以
表示点P与点V(3)的距离,所以
Prjn(PV (3))>Prjn(PV (1))
其中:Prjn(PV (3))表示线段PV (3)相对于直线π的垂足的长度,这说明F(V (3))>F(V (1)),与假设相矛盾。因此定理得证。
定理3 如图2所示,假设二元混合变量线性规划问题(11)在连续变量空间中的全局最优解是与目标函数直线簇平行的线段P1P2上的所有点,则:
(1) 混合变量全局最优解即为线段P1P2上的混合变量可行解,且混合变量全局最优函数值与连续变量全局最优函数值相等;
(2) 若线段P1P2上没有混合变量可行解,假设按定理2求得的对应于线段P1P2上任意一个连续变量全局最优解P的混合变量全局最优解为VP,则该规划问题的混合变量全局最优解为
V*=VP
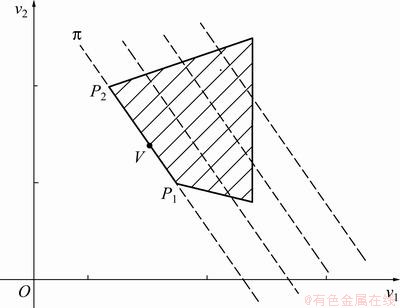
图2 定理3的几何表示
Fig.2 Geometric representation for Theorem 3
证明:由于线段P1P2上的混合变量可行解在原问题连续全局最优解集之中,因此,它们必为混合变量全局最优解。又假设还有不在线段P1P2上的混合变量全局最优解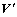 ,由图解之,必有F(
,由图解之,必有F(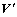 )>F(V)(其中,V为线段P1P2上的任意一个混合变量可行解),这与假设不符。由于线段P1P2上的混合变量可行解与连续变量全局最优解同在直线π上,因而对应目标函数值相等。因此结论(1)成立。
)>F(V)(其中,V为线段P1P2上的任意一个混合变量可行解),这与假设不符。由于线段P1P2上的混合变量可行解与连续变量全局最优解同在直线π上,因而对应目标函数值相等。因此结论(1)成立。
结论2可由定理2直接证得。
对于模型(9),可又将其转化成二元混合变量线性规划形式,从而可利用定理2和定理3求解。
在模型(9)中,令V=(v1,v2)T=(3y1+y3,y2),则模型(9)转化为:
min W(V)=ln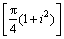 +v1+3v2
+v1+3v2
s.t. v1+3v2≥A1
v1+2.206106 v2≥A2;17≤x2≤25
v1+2.064695 v2≥A3;25≤x2≤60
v1+2.064695 v2≥A4;25≤ix2≤60
v1+1.983595 v2≥A5;60≤ix2≤300
3lnC1+lnC5≤v1≤3lnC2+lnC6
lnC3≤v2≤lnC4; (12)
v1=3y1+y3,v2=y2;
yi=lnxi;i=1, 2, 3;
x=(x1, x2, x3)T∈Ω×Z+×R+
如果去掉模型(12)中的后3个约束,则得到仅含2个决策变量的线性规划问题。由定理2和定理3可解得模型(12)的混合变量全局最优解V*=(v1*, v2*)T。
对如下子问题:
v1*=3y1+y3
lnC1≤y1≤lnC2
lnC5≤y3≤lnC6 (13)
yi=lnxi,i=1, 3
(x1, x3)T∈Ω×R+
可进一步将其分解为以下2个子问题:
min 3y1+y3
s.t. 3y1+y3-v1*≥0
lnC1≤y1≤lnC2 (14)
lnC5≤y3≤lnC6
yi=lnxi, i=1, 3
(x1, x3)T∈Ω×R+
和
min -3y1-y3
s.t. 3y1+y3-v1*≤0
lnC1≤y1≤lnC2 (15)
lnC5≤y3≤lnC6
yi=lnxi; i=1, 3
(x1, x3)T∈Ω×R+
按定理2和定理3求得这2个子问题的解,它们的交集即为子问题(13)的解。
4 实际设计案例研究
利用前面提出的求解含混合变量的线性规划问题的全局寻优方法来优化一类典型的直齿轮传动设计问题,并将它与普通优化设计方法进行比较。
试设计1对闭式直齿圆柱齿轮传动。已知:主动轮的输入扭矩T1=1×105 N·mm,齿数比i=4,单向传动,轴承对齿轮对称布置。小齿轮采用45钢,调质,齿面硬度为250~280,齿面接触强度的许用应力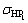 =680 N/mm2,齿根弯曲强度的许用应力
=680 N/mm2,齿根弯曲强度的许用应力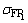 =288 N/mm2。大齿轮采用45钢,调质,齿面硬度220~250 HBS,齿面接触强度的许用应力
=288 N/mm2。大齿轮采用45钢,调质,齿面硬度220~250 HBS,齿面接触强度的许用应力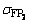 =550 N/mm2,齿根弯曲强度的许用应力
=550 N/mm2,齿根弯曲强度的许用应力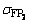 =204 N/mm2。要求结构紧凑。假设该齿轮副为经过齿向修形和齿廓修形的高精度齿轮,其载荷系数K为1.21。
=204 N/mm2。要求结构紧凑。假设该齿轮副为经过齿向修形和齿廓修形的高精度齿轮,其载荷系数K为1.21。
根据该设计条件,由文献[15]可得其优化模型约束条件中的常系数值如表1所示。
表1 实际设计问题中参数的取值
Table 1 Values of parameters in real design problem

将各常系数值代入模型(12)。该实例的全局寻优示意图如图3所示。图3中阴影部分为该优化问题的可行域,而一簇平行虚线表示不同取值时的目标函数。当目标虚线移动到与可行域最左端边界相切时模型(12)的目标函数取得最小值,此时该实例在连续变量空间中的全局最优解即为切线段P1P2中的各点,可表示为
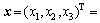
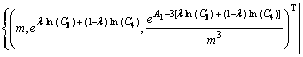
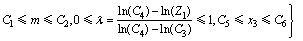 (16)
(16)
由于线段P1P2表示模型(12)第一个约束的一部分边界线,这说明第一个约束即齿面接触强度的性能约束是该优化问题的有效约束。
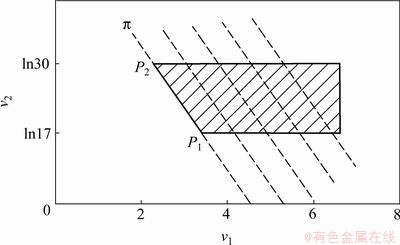
图3 全局寻优示意图
Fig.3 Diagram for global optimization method
通过式(16)还可以解得线段P1P2上的所有混合变量可行解如表2所示。由定理3知,这些可行解即为本实例的全体混合变量全局最优解,对应的最优值均为3.006 2×106。
以往传动设计优化中,常利用科学与工程计算软件包(如MATLAB)求解所建立的优化模型[17],或者应用某些局部优化方法,如罚函数方法和坐标轮换法[18],求解相应的优化模型。把这些方法直接应用于求解上述设计案例,计算结果如表3所示。由于这些局部优化方法只能求解连续变量的优化模型,为此,把计算结果采用圆整方法得到实际传动设计方案。表3所示为采用4种常规优化算法求得圆整前后的最优解及对应的最优目标函数值。
表2 全局优化方法的求解结果
Table 2 Results from global optimization method

表3 4种常规优化算法与全局优化方法比较
Table 3 Comparison between four ordinary methods and global optimization method
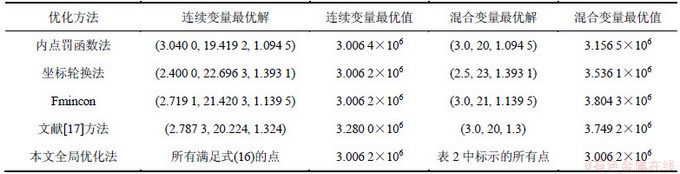
表3中,Fmincon是指利用MATLAB优化工具箱中的Fmincon指令求解的方法。采用坐标轮换法和Fmincon函数法时,对于不同的初始值,可解得不同的连续变量最优解,但所对应的目标函数最优值均为3.006 2×106,这与本文图解分析该案例时得到连续变量最优解数目为无穷多个的结果相一致。
注意到表3中有2种局部优化算法的连续变量最优值与本文全局优化方法求解混合变量问题时得到的目标函数最优值相同,其重要区别在于:局部优化算法不能保证解的全局最优性。事实上,能够证明,模型(8)的目标函数F(x)在R3 +中其Hessian阵的一阶和三阶主子式恒为正,而二阶主子式恒为负,即F(x)在R3 +中是非凸函数。这意味着任何局部优化算法都无法从理论上保证所得到的结果具有全局最优性。同时,局部优化算法得到的解还必须经过圆整,而由表3所示结果知,其圆整解要劣于本文方法求得的混合变量最优解。但本文提出的全局寻优方法所求得的最优解不需要圆整,能直接用于实际工程设计优化,从而提高设计方案的可靠性;并且能够得到所有全局最优解,这为降低优化设计成本提供了重要依据。
5 结论
(1) 针对一类载荷系数一定的直齿圆柱齿轮传动的体积优化设计问题,建立了数学模型。基于一种变量变换方法,将原非线性优化模型转化成了含混合变量的线性规划模型。
(2) 设计混合变量线性规划问题的全局优化方法。
(3) 将该方法应用于研究典型的直齿圆柱齿轮优化设计案例,在含有连续变量和离散变量的可行域中求得所有全局最优设计方案。与普通优化方法比较,本文提出的全局寻优方法优于已有局部优化方法。
参考文献:
[1] Faruk M, Tamer B, Kurtulus B, et al. Optimization of module, shaft diameter and rolling bearing for spur gear through genetic algorithm[J]. Expert Systems with Applications, 2010, 37(12): 8058-8064.
[2] Savsani V, Rao R V, Vakharia D P. Optimal weight design of a gear train using particle swarm optimization and simulated annealing algorithms[J]. Mechanism and Machine Theory, 2010, 45(3): 531-541.
[3] 顾勇, 高一知. 三级圆柱齿轮传动的系列优化设计算法探析[J]. 四川理工学院学报: 自然科学版, 2009, 22(2): 105-107.
GU Yong, GAO Yizhi. Three cylindrical gear series of optimal design of algorithms[J]. Journal of Sichuan University of Science & Engineering: Natural Science Edition, 2009, 22(2): 105-107.
[4] Faggioni M, Samani F S, Bertacchi G, et al. Dynamic optimization of spur gears[J]. Mechanism and Machine Theory, 2011, 46(4): 544-557.
[5] 彭程, 肖志信. 齿轮传动模糊可靠性优化设计[J]. 机械传动, 2006, 30(4): 42-43, 46.
PENG Cheng, XIAO Zhixin. Fuzzy reliability optimal design of gear transmission[J]. Journal of Mechanical Transmission, 2006, 30(4): 42-43, 46.
[6] 姚英姿, 樊俊星, 莫云辉, 等. 基于模糊理论和遗传算法的航空齿轮可靠性优化设计[J]. 上海大学学报: 自然科学版, 2004, 10(4): 362-366.
YAO Yingzi, FAN Junxing, MO Yunhui, et al. Reliability optimization of aviation gears based on fuzzy theory and genetic algorithm[J]. Journal of Shanghai University: Natural Science Edition, 2004, 10(4): 362-366.
[7] Lucian T, Ovidiu B, Cornel S, et al. Automated optimal design of a two-stage helical gear reducer[J]. Struct Multidisc Optim, 2010, 42(3): 429-435.
[8] Rao R V, Savsani V J. Mechanical design optimization using advanced optimization techniques[M]. London: Springer-Verlag, 2012: 1-4.
[9] Floudas C A, Gounaris C E. A review of recent advances in global optimization[J]. Journal of Global Optimization, 2009, 45(1): 3-38.
[10] ZHANG Shaojun, WAN Zhong, LIU Guanglian. Global optimization design method for maximizing the capacity of V-belt drive[J]. Science China: Technological Sciences, 2011, 54(1): 140-147.
[11] 张少军, 万中, 刘光连. V带疲劳寿命最长的全局优化设计[J]. 中国机械工程, 2011, 22(4): 403-407.
ZHANG Shaojun, WAN Zhong, LIU Guanglian. Global optimization design of V-belt fatigue life[J]. China Mechanical Engineering,2011, 22(4): 403-407.
[12] 濮良贵, 纪名刚. 机械设计[M]. 7版. 北京: 高等教育出版社, 2001: 190-200.
PU Lianggui, JI Minggang. Mechanical design[M]. 7th ed. Beijing: Higher Education Press, 2001: 190-200.
[13] 王文博. 机构和机械零部件优化设计[M]. 北京: 机械工业出版社, 1990: 229-232.
WANG Wenbo. Optimal design of mechanism and mechanical elements[M]. Beijing: China Machine Press, 1990: 229-232.
[14] GB/T 3480—1997, 渐开线圆柱齿轮承载能力计算方法[S].
GB/T 3480—1997, Calculation methods of load capacity for involute cylindrical gears[S].
[15] 机械设计手册编委会. 机械设计手册: 齿轮传动[M]. 北京: 机械工业出版社, 2008: 43-54.
Mechanical Design Handbook Editorial Board. Mechanical design handbook: Gear drive[M]. Beijing: China Machine Press, 2008: 43-54.
[16] 张安宁, 童小燕. 混合变量优化设计的整型化方法[J]. 西北工业大学学报, 2003, 21(5): 548-551.
ZHANG Anning, TONG Xiaoyan. On better optimization through turning mixed variables into completely-integer ones[J]. Journal of Northwestern Polytechnical University, 2003, 21(5): 548-551.
[17] 韩秀梅, 罗学科. 齿轮传动的模糊优化设计[J]. 北方工业大学学报, 2004, 16(3): 48-52.
HAN Xiumei, LUO Xueke. Research on fuzzy optimization of gear-driven system[J]. Journal of North China University of Technology, 2004, 16(3): 48-52.
[18] 刘惟信. 机械最优化设计[M]. 2版. 北京: 清华大学出版社, 1994: 65-70, 211-223.
LIU Weixin. Mechanical optimal design[M]. 2nd ed. Beijing: Tsinghua University Press, 1994: 65-70, 211-223.
(编辑 邓履翔)
收稿日期:2012-06-28;修回日期:2012-08-20
基金项目:国家自然科学基金资助项目(71221061, 70921001)
通信作者:万中(1966-),男,江西都昌人,教授,从事优化方法及应用研究;电话:18684928167;E-mail: wanmath@163.com
摘要:分析现有齿轮传动优化设计方法在全局优化方面的不足。针对一类载荷系数一定的直齿圆柱齿轮传动设计的体积优化问题,建立非线性优化模型。基于模型特点的分析,采用变量组合与取自然对数的变量变换方法,将原非线性问题等价地转化为含混合变量的线性规划模型,并设计一类求解混合变量的线性规划问题的全局优化方法。将这一系列方法应用于研究典型的直齿圆柱齿轮传动优化设计案例,并与已有设计优化方法比较。结果表明:该全局优化方法得到的大小齿轮分度圆柱体积小于其他方法得到的圆整最优值。
[3] 顾勇, 高一知. 三级圆柱齿轮传动的系列优化设计算法探析[J]. 四川理工学院学报: 自然科学版, 2009, 22(2): 105-107.
[5] 彭程, 肖志信. 齿轮传动模糊可靠性优化设计[J]. 机械传动, 2006, 30(4): 42-43, 46.
[6] 姚英姿, 樊俊星, 莫云辉, 等. 基于模糊理论和遗传算法的航空齿轮可靠性优化设计[J]. 上海大学学报: 自然科学版, 2004, 10(4): 362-366.
[11] 张少军, 万中, 刘光连. V带疲劳寿命最长的全局优化设计[J]. 中国机械工程, 2011, 22(4): 403-407.
[12] 濮良贵, 纪名刚. 机械设计[M]. 7版. 北京: 高等教育出版社, 2001: 190-200.
[13] 王文博. 机构和机械零部件优化设计[M]. 北京: 机械工业出版社, 1990: 229-232.
[14] GB/T 3480—1997, 渐开线圆柱齿轮承载能力计算方法[S].
[15] 机械设计手册编委会. 机械设计手册: 齿轮传动[M]. 北京: 机械工业出版社, 2008: 43-54.
[16] 张安宁, 童小燕. 混合变量优化设计的整型化方法[J]. 西北工业大学学报, 2003, 21(5): 548-551.
[17] 韩秀梅, 罗学科. 齿轮传动的模糊优化设计[J]. 北方工业大学学报, 2004, 16(3): 48-52.
[18] 刘惟信. 机械最优化设计[M]. 2版. 北京: 清华大学出版社, 1994: 65-70, 211-223.


