J. Cent. South Univ. Technol. (2010) 17: 449-453
DOI: 10.1007/s11771-010-0505-5 
Fracture prediction in non-isothermal viscous pressure bulging of
aluminum alloy sheet using ductile fracture criterion
WANG Zhong-jin(王忠金), LIU Jian-guang(刘建光), LI Yi(李毅)
School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract:
The failure of AA3003 aluminum alloy sheet metal was predicted for non-isothermal viscous pressure bulging (VPB). Utilizing the coupled thermo-mechanical finite element method combined with ductile fracture criterion, the calculations were carried out for non-isotherm VPB at various temperatures and the influences of the initial temperature of viscous medium on failure mode of bulge specimens were investigated. The results show that the failure modes are different for the non-isothermal VPB with different initial temperatures of viscous medium. For the non-isothermal VPB of AA3003 aluminum alloy sheet with initial temperature of 250 ℃, when the initial temperature of viscous medium ranges from 150 to 180 ℃, the formability of sheet metal can be improved to a full extent. The validity of the predictions is examined by comparing with experimental results.
Key words:
1 Introduction
The need for fuel savings and structural weight reduction in aerospace and automobile industries is driving the replacement of steel by lightweight materials. Aluminum has a large potential for weight reduction, but press operations of it are more critical than those with steel. The formability of aluminum alloy can be improved by changing the forming temperature to either cryogenic or elevated temperatures [1-5].
Non-isothermal viscous pressure forming is a new sheet warm forming process developed by authors based on the viscous pressure forming (VPF) at room temperature [6-7]. The viscous pressure-carrying medium is heated to various temperatures in non- isothermal viscous pressure forming process. Because of the low heat conductivity of viscous medium, the non- uniform temperature distribution is formed in viscous medium and sheet metal, which makes it possible to manipulate the local flow of sheet metal [8].
Prediction of fracture during sheet metal forming is important to optimize process parameters and die structure. In recent years, more and more attention has been paid to using the ductile fracture criterion to predict the forming limit in metal forming, such as hydroforming, blanking and deep drawing [9-12]. But most of studies have been concentrated on predicting the fracture of sheet metal at room temperature. Few of researchers have carried out the failure prediction for warm forming [13].
In this work, the failure was predicted for non- isothermal viscous pressure bulging of AA3003 aluminum alloy sheet by using the coupled thermo- mechanical finite element method combined with ductile fracture criterion. The calculations were carried out for non-isotherm viscous pressure bulging (VPB) at various temperatures and the influences of initial temperature of viscous medium on the failure mode of bulge specimens were investigated. The optimum forming temperature was determined. Through comparing the numerical simulation results with experimental ones, the validity of the predictions was examined.
2 Numerical simulation procedures
2.1 Finite element (FE) model of non-isothermal VPB
The commercial finite element analysis software DEFORM2D was used for the simulation of the non-isothermal VPB of aluminum alloy sheet. FE model is shown in Fig.1. The diameter of sheet blank is 86 mm and the initial thickness is 0.5 mm. The diameter of inlet port is 56 mm. The radius of die corner profile is 3 mm. The velocity of piston is 0.2 mm/s. The Coulomb friction rule is used to describe the interfacial condition and the frictional coefficient at sheet/die interface is 0.1. The interfacial condition at sheet/medium interface is modeled by shear friction model and the friction factor is 0.2. Sheet metal is formed under the pressure of viscous medium pumped by piston. Rigid part needs to be meshed to calculate the heat exchange and investigate the influence of temperature distribution. So it is a thermomechanical coupled deformation. Analysis is realized on half of the geometry because of axisymmetry of the model. Sheet metal is meshed with quadrilateral element. These elements have both temperature and displacement as their degrees of freedom to predict both deformation and temperature variation during the process. The initial temperature parameters of each part of the model are listed in Table 1. The initial temperature of viscous medium tv varies from 20 to 230 ℃. The initial temperature of sheet blank keeps at 250 ℃. The failure characteristics are investigated through varying the initial temperature of viscous medium and the optimum forming temperature parameters are determined to improve the formability to a full extent.
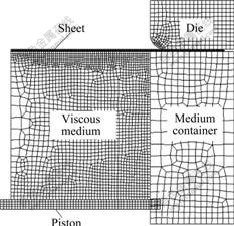
Fig.1 Finite element analysis model of non-isothermal VPB
Table 1 Temperature parameters used in simulations
2.2 Experimental materials
In this work, AA3003 aluminum alloy was selected to do the investigation. A temperature-dependent material model was selected to describe the deformation behavior of aluminum alloy at warm temperature, including the effect of temperatures and strain rate. The material model is expressed as
(1)
where 
is the flow stress; t is the temperature of sheet metal; K is the strength hardening coefficient; n is the strain-hardening exponent; m is the strain-rate sensitivity index; 
denotes the effective plastic strain; 
is the strain rate; 
is a constant representing the elastic strain to yield; and 
is a reference strain rate (a constant).
The flow stress-strain curves of AA3003 sheet at different temperatures were obtained by ABEDRABBO et al [4]. K, n and m are related to temperature. They can be expressed as the following equations through fitting the stress-strain curves obtained by carrying out tensile tests:
K=-0.505 8 t+210.40
n=-0.000 4 t+0.218 5
m=0.001 8 exp(0.014 7 t)
Thermal parameters of AA3003 aluminum alloy sheet and viscous medium are shown in Table 2. The thermal parameters of viscous medium are obtained by experiments. Viscous medium used in this work is a kind of polymer whose mechanical properties are insensitive to temperature. The mean thermal conductivities of aluminum alloy sheet and viscous medium are 180 and 0.2 W/(m·℃), respectively. It can be said that the viscous medium is a poor heat conductor. So, visco-plastic material model is used in numerical simulation of warm forming. The material model tested at room temperature is as follows:
(2)
Table 2 Thermal parameters used in simulation
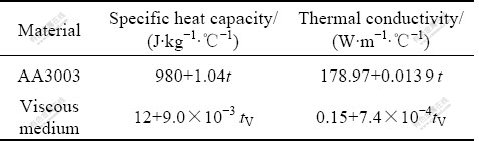
3 Ductile fracture criterion
3.1 Cockroft-Latham fracture criterion
The Cockroft-Latham fracture criterion can be expressed as [14]
(3)
where 
and 
are the increments of effective strain and effective stress, respectively; 
is the maximum principle stress; and C is the damage value.
Rewriting Eq.(3) provides integral I
(4)
Using the values of 
and obtained by the finite element simulation and the material constants Ccri when fracture occurs, integral I is calculated for each element at each deformation step. The condition of fracture is satisfied when and where integral I amounts to unity.
3.2 Determination of critical damage value at warm temperature
In order to apply the Cockroft-Latham ductile fracture criterion, the critical damage value Ccri must be determined firstly. In this work, the uniaxial tension tests were conducted to determine Ccri. The relationship between Ccri and uniaxial tension fracture strain is derived as follows. Ignoring the anisotropic property of sheet metal, the von Mises yield criterion is used.
(5)
where σ1, σ2 and σ3 are the direct stress components; τ12, τ23 and τ13 are the shear stress components.
For sheet uniaxial tension,
,
(6)
So
;
; =
(7)
For the uniaxial tension condition, material constant C in Cockroft-Latham ductile fracture criterion when fracture occurs is equal to the fracture strain
(8)
According to uniaxial tension tests at various temperatures [5], the fracture strains in tension test can be measured. The relationship between the critical damage value and temperature is shown in Fig.2. Through fitting the curve, the critical damage can be expressed as the function of temperature:
Ccri=1.420 48×10-6t2+1.828 62×10-4t+0.285 13 (9)
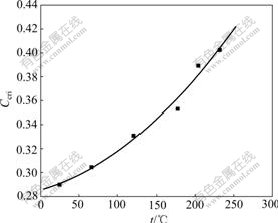
Fig.2 Relationship between critical damage value and temperature
4 Fracture analysis
In order to analyze the failure characteristics of bulge specimen at various initial temperatures of viscous medium, the distributions of the ductile fracture integral value I of bulge specimen calculated from Eq.(4) in numerical simulations were investigated at initial temperatures of viscous medium, 20, 150 and 200 ℃.
The coordinate system of deformed mesh is shown in Fig.3. Fig.4(a) presents the distribution of the ductile
Fig.3 Coordinate system of deformed mesh
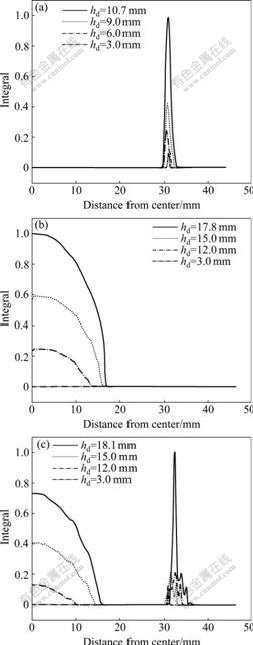
Fig.4 Distributions of calculated integral of bulge specimens for non-isothermal VPB with various initial temperatures of viscous medium: (a) tV=20 ℃; (b) tV=200 ℃; (c) tV=150 ℃
fracture integral I when the initial temperature of viscous medium is 20 ℃. During the deformation, the maximum integral I locates at the contact edge with die corner. As the deformation proceeds, the integral I increases continuously. When the bulge dome height (hd) of specimen attains 13 mm, the maximum integral I approaches 1.0 and the predicted failure occurs at this location. Integral I at dome height keeps lower value during the forming.
The distributions of the ductile fracture integral I are shown in Fig.4(b) for the case of the initial temperature of viscous medium 200 ℃. Different from the former forming condition, the maximum integral I locates at dome center and integral I at the contact edge with low die corner during the deformation. At the bulge dome height of 17.8 mm, integral I approaches 1.0 and the predicted failure happens.
The distributions of the ductile fracture integral value I when the initial temperature of viscous medium is 150 ℃ are shown in Fig.4(c). At the beginning of bulging process, the maximum integral value I locates at dome center. As the deformation proceeds, integral value I at the contact edge with die corner increases gradually.
Two peaks form for the distribution curve of the ductile fracture integral I. Integral I at the contact edge when die corner reaches 1.0 at bulge dome height of 18.1 mm and that at dome center is 0.73.
The distributions of the ductile fracture integral value I for each forming cases when the predicted failure occurs are shown in Fig.5. The location of failure changes dramatically with initial temperature of viscous medium. The predicted limit dome height (hld) of bulge specimen when the maximum fracture integral value I approaches 1.0 for each forming temperature is shown in Fig.6. The predicted hld does not vary monotonously with the variation of initial temperature of viscous medium. The predicted hld increases with increasing the initial temperature of viscous medium at the critical temperature 150 ℃. The bulging hld increases from 13.0
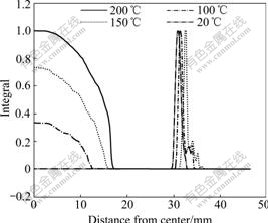
Fig.5 Distributions of calculated integral of bulge specimens at limit bulge height
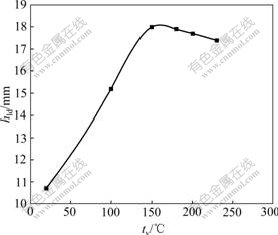
Fig.6 hld distributions with various initial temperatures of viscous medium
to 18.1 mm, corresponding to a 37% increase. When the initial temperature of viscous medium increases from 180 ℃ to that of sheet metal, the predicted hld decreases gradually. When the initial temperature of viscous medium ranges from 150 to 180℃, the formability of sheet metal can be improved to a full extent.
The experimental bulging specimens for the initial temperature of viscous medium of 20 ℃ and 200 ℃ are shown in Fig.7. At the initial temperature 200 ℃ of viscous medium, the fracture position of sheet metal locates at the dome center at the bulge height of 17.4 mm. The fracture point occurs at the contact edge with die corner at initial temperature 20 ℃ and the limit dome height is 13.3 mm. The sites of failure prediction in this work are in good agreement with those of the actual bulging tests. The fully coupled thermo-mechanical finite element analysis model is able to accurately predict both the limit dome height and location in the sheet at various temperatures.
5 Conclusions
(1) In non-isothermal VPB, the initial temperature of viscous medium has an obvious effect on the fracture location of bulge specimen. When the initial temperature of viscous medium is low, the failure site of bulge specimen locates at the contact edge with die corner. Increasing the initial temperature of viscous medium to the temperature of sheet metal gradually, the maximum damage value location gradually moves to dome center. It can be predicted that when the ductile fracture maximum integral value at dome center and the contact edge with die corner approaches to 1.0 synchronously, the height of bulge specimens reaches the highest.
(2) For the non-isothermal VPB of AA3003 aluminum alloy sheet with an initial temperature of 250 ℃, when the initial temperature of viscous medium ranges from
Fig.7 Experimentally observed and numerical simulation predicted fracture location: (a) Experiment specimen at tV= 20 ℃; (b) Experiment specimen at tV=200 ℃; (c) Predicted specimen at tV=20 ℃; (d) Predicted specimen at tV=200 ℃
150 to 180 ℃, the formability of sheet metal can be improved to a full extent.
(3) Comparison of calculated results with experimental ones shows that the failure sites and limit bulging height are successfully predicted using the coupled thermo-mechanical finite element method combined with ductile fracture criterion for non-isothermal viscous pressure bulging.
References
[1] TOROS S, OZTURK F, KACAR I. Review of warm forming of aluminum-magnesium alloys [J]. Journal of Materials Processing Technology, 2008, 207(1/3): 1-12.
[2] KIM H S, KOC M. Numerical investigations on springback characteristics of aluminum sheet metal alloys in warm forming conditions [J]. Journal of Materials Processing Technology, 2008, 204(1/3): 370-383.
[3] ABEDRABBO N, POURBOGHRAT F, CARSLEY J. Forming of AA5182-O and AA5754-O at elevated temperatures using coupled thermo-mechanical finite element models [J]. International Journal of Plasticity, 2007, 23(5): 841-875.
[4] ABEDRABBO N, POURBOGHRAT F, CARSLEY J. Forming of aluminum alloys at elevated temperatures (Part 1): Material characterization [J]. International Journal of Plasticity, 2006, 22(2): 314-341.
[5] LI D, GHOSH A K. Biaxial warm forming behavior of aluminum sheet alloys [J]. Journal of Materials Processing Technology, 2004, 145(3): 281-293.
[6] WANG Z J, LIU J G, WANG X Y, HU Z Y, GUO B. Viscous pressure forming (VPF): State-of-the-art and future trends [J]. Journal of Materials Processing Technology, 2004, 151(1/3): 80-87.
[7] LIU J, AHMETOGLU M, ALTAN T. Evaluation of sheet metal formability, viscous pressure forming (VPF) dome test [J]. Journal of Materials Processing Technology, 2000, 98(1): 1-6.
[8] LIU J G, PENG Q C, LIU Y, WANG Z J. Viscous pressure bulging of aluminum alloy sheet at warm temperatures [J]. Journal of Mechanical Science and Technology, 2007, 21(10): 1338-1345.
[9] NAKA T, NAKAYAMA Y, UEMORI T, HINO R, YOSHIDA F, KOHZU M, HIGASHI K. FLD of AZ31 sheet under warm stretching and its prediction [J]. International Journal of Modern Physics B, 2008, 22(31/32): 6010-6015.
[10] YU S, XIE X, ZHANG J, ZHAO Z. Ductile fracture modeling of initiation and propagation in sheet-metal blanking processes [J]. Journal of Materials Processing Technology, 2007, 187/188: 169-172.
[11] KO Y K, LEE J S, HUH H, KIM H K, PARK S H. Prediction of fracture in hub-hole expanding process using a new ductile fracture criterion [J]. Journal of Materials Processing Technology, 2007, 187: 358-362.
[12] JAIN M, ALLIN J, LLOYD D J. Fracture limit prediction using ductile fracture criteria for forming of an automotive aluminum sheet [J]. International Journal of Mechanical Sciences, 1999, 41(10): 1273-1288.
[13] ALEXANDROV S, WANG P T, ROADMAN R E. A fracture criterion of aluminum alloys in hot metal forming [J]. Journal of Materials Processing Technology, 2005, 160(2): 257-265.
[14] COCKROFT M G, LATHAM D J. Ductility and the workability of metals [J]. Journal of the Institute of Metals, 1968, 96: 33-39.
Foundation item: Projects(50805034, 50275035) supported by the National Natural Science Foundation of China
Received date: 2009-09-28; Accepted date: 2009-12-15
Corresponding author: LIU Jian-guang, PhD; Tel: +86-451-86413365; E-mail: liujg@hit.edu.cn
(Edited by YANG You-ping)
