Article ID: 1003-6326(2005)02-0291-05
Modeling of solidification grain structure for Ti-45%Al alloy ingot by cellular automaton
WU Shi-ping(吴士平), LIU Dong-rong(刘东戎),
GUO Jing-jie(郭景杰), FU Heng-zhi(傅恒志)
(School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China)
Abstract:
A cellular automaton model for simulating grain structure formation during solidification processes of Ti-45%Al(mole fraction) alloy ingot was developed, based on finite differential method for macroscopic modeling of heat transfer and a cellular automaton technique for microscopic modeling of nucleation, growth, solute redistribution and solute diffusion. The relation between the growth velocity of a dendrite tip and the local undercooling, which consists of constitutional, thermal, curvature and attachment kinetics undercooling is calculated according to the Kurz-Giovanola-Trivedi model. The effect of solidification contraction is taken into consideration. The influence of process variables upon the resultant grain structures was investigated. Special moving allocation technique was designed to minimize the computation time and memory size associated with a large number of cells. The predicted grain structures are in good agreement with the experimental results.
Key words:
Ti-45%Al alloy; cellular automaton; solidification grain structure CLC number: TG27;
Document code: A
1 INTRODUCTION
Properties of casting are greatly affected by the grain structures that are essentially determined by the solidification behavior during the casting. The parameters that affect the solidification behavior and subsequent grain morphology include mold dimension, pouring temperature, mold-preheated temperature and alloy composition, etc. Thus, the number of possible combinations for all design and process condition is enormous. If the conventional approach of trial-and-error is employed to obtain the optimal design for the casting processes, it will be costly and time consuming.
Therefore, there is a considerable potentiality of computer simulation for this purpose. Extensive efforts have been made to develop various kinds of deterministic and stochastic models to predict the evolution of microstructures in solidification of alloys[1-13]. Compared with the deterministic models, stochastic models have advantages as follows. 1) They produce metallographic sections that can be directly compared with experimental micrographs. 2) They can account for both columnar and equiaxed structures. It has been demonstrated that the occurrence of the outer equiaxed zone, the columnar zone, the elongated and equiaxed grains, can be explained by a unique set of nucleation parameters and a single growth kinetics. These different morphologies are then merely determined by the local thermal conditions (temperature gradient, speed of the isotherms). 3) The grain competition that occurs in the columnar zone can also be simulated by such methods.
In recent years, the modeling of the microstructural formation in material processing has progressed markedly based on stochastic cellular automaton(CA) technique. Cho et al[14] have studied the microstructural formation and columnar-to-equiaxed transition(CET) in squeeze casting of Al-4.5%Cu(mass fraction) alloy. Lee et al[15] have predicted the columnar dendritic growth in a flowing melt and solidification grain structure formation in centrifugal casting of Al-Si alloy[16]. Gandin et al[17] have developed a three-dimensional CA model for the prediction of dendritic grain structures of a pigtail grain selector and aluminum-silicon rods. These computer-based predictive models for linking casting conditions to microstructures of the materials, can describe the major phenomena that control the solidification processes, and has become powerful tools in studying the microstructural formation and evolution involving nucleation and growth of grains. However few such calculations have been performed to simulate the grain structure formation during the solidification processes of Ti-Al alloy ingot.
In this study, a CA model for simulating grain structure formation during solidification processes of Ti-45%Al alloy ingot is developed. Finite differential method(FDM), which is coupled with the CA technique, is used to calculate the temperature and solute fields in the calculation domain. The influence of solidification contraction on the solidification processes is studied. The effect of process variables upon the resultant grain structures is investigated. Special moving allocation technique is designed to minimize the computation time and memory size. Solidification grain structures predicted by this model are compared with the experimental results.
2 COMPUTING MODEL FOR GRAIN STRUCTURE SIMULATION
2.1 Governing equations
Neglecting the effect of convection, the solidification process is controlled by thermal transfer and solute diffusion. The thermal transfer equation is
![]()
where ρ is the density, cp is the specific heat, λL is the thermal conductivity, L is the latent heat, and fs is the solid fraction.
Solute diffusion equation in liquid is
![]()
Solute diffusion equation in solid is
![]()
Local solute equilibrium at the S/L interface is
C*s=kC*l(4)
where Dl and Ds are liquid diffusion and solid diffusion coefficients, respectively, k is the partition coefficient, C*s is solid concentration at s/l interface, and C*l is liquid concentration at s/l interface.
2.2 Nucleation model
Gaussian law is used in the continuous nucleation model:
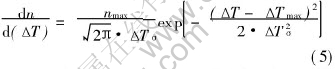
where nmax is the maximum nuclei density, ΔTσ and ΔTmax are the standard deviation and the mean nucleation undercooling, respectively.
2.3 Growth kinetics
During the solidification processes, the total undercooling at dendrite tips are contributed by the following four items as
ΔT=ΔTc+ΔTt+ΔTr+ΔTk(6)
where ΔTc, ΔTt, ΔTr and ΔTk are the undercooling contributions associated with solute diffusion, thermal diffusion, solid-liquid interface curvature and attachment kinetics, respectively. For most metallic alloys, when solidified under normal solidification conditions, the last three contributions that appear on the right hand side of Eqn.(6) are small, and solute undercooling predominates.
The growth kinetics of both columnar and equiaxed dendrites can be calculated with the aid of the Kurz-Giovanola-Trivedi (KGT) model[18] as
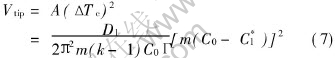
where Vtip is the growth velocity at the dendrite tip, A is growth constant, m is the liquidus slope, C0 is the initial alloy composition and Γ is the Gibbs-Thomson coefficient, k is the partition coefficient; C*l is liquid concentration at s/l interface.
2.4 CET model
In this paper, the CET model[19] is taken as
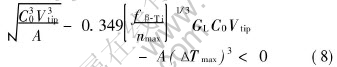
where fβ -Ti is solid fraction of β -Ti at peritectic reaction temperature. Eqn.(8) is the limit for fully columnar growth.
3 SPECIAL MOVING ALLOCATION TECHNIQUE(SMA)
In order to minimize the computation time and memory size associated with a very large number of cells, special moving allocation technique is designed. SMA is associated with the temperature and position of elements in the calculation domain. Fig.1 shows a schematic representation of SMA technique. In this paper, elements are divided into three groups preliminarily. If one element of the group is in the mushy zone, the elements in the same group are subdivided into cells and allocated memory, and this group is tagged as “Active”. When the temperature of all elements of the same group drops below the solidus temperature Ts, the memory is freed and this group is tagged as “Inactive”. If temperature of all elements in the group is larger than liquidus temperature Tl, this group is not considered and also tagged as “Inactive”. During solidification processes, groups are activated, and then deactivated as the mushy zone moves across the calculation domain. Only local part of the ingot is studied. By means of SMA, computation costs are minimized.
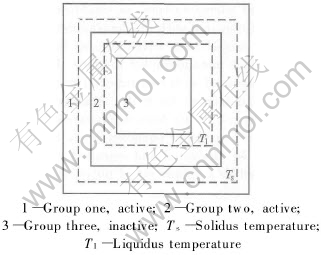
Fig.1 Schematic illustration of special moving allocation technique
4 RESULTS AND DISCUSSION
The present stochastic model is applied to simulate the grain structure formation and evolution during the solidification processes of Ti-45%Al alloy ingot. The schematic of the two-dimensional ingot vertical section is shown in Fig.2. The thermodynamic data needed for calculation is taken from Ref.[20].
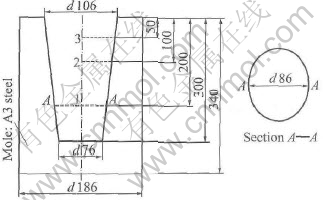
Fig.2 Schematic illustration of ingot and mould(mm)
As it solidifies, the ingot shrinks and an air gap forms at the metal and mold interface. This further affects the heat transfer significantly. Thus, a critical part in realistically simulating solidification of ingot is the specification of the boundary conditions due to solidification contraction. In this paper, it is assumed that an intimate contact between the metal and mold exists while the former is liquid, but, as solidification proceeds, the metal shrinks, forming an air gap at the interface, which reduces the heat transfer rate. The detailed characterization of boundary conditions required to describe the temperature evolution in the ingot is summarized in Table 1.
Figs.3 illustrates the effect of the solidification contraction on the cooling curves at the points 1, 2 and 3, as shown in Fig.2. As indicated in
Table 1 Boundary conditions used for thermal analysis

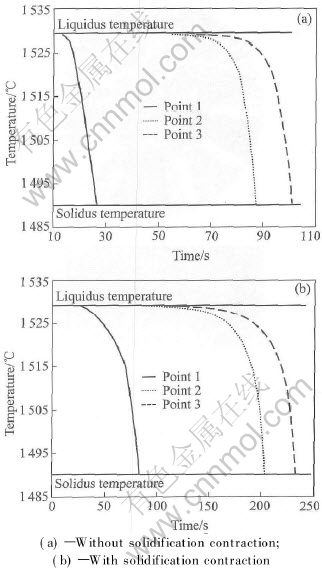
Fig.3 Effect of solidification contraction on calculated cooling curves
Fig.3(a), the ingot is cooled at a faster rate. This is due to, without consideration of solidification contraction, that no air gap is formed between the metal and mold interface, which enhances the heat transfer from the metal to the mold. With consideration of solidification contraction, once the interfacial solid shell has fully developed, the interface contact mode between the melt and mold surface is changed from a tight contact to a mechanical contact as shrinkage grows, leading to dramatic decrease of the heat transfer. As indicated in Fig.3(b), solidification proceeds at a slower rate.
Fig.4 indicates the predicted and experimental solidification grain structures for the solidification of Ti-45%Al alloy ingot with pouring temperature of 1600℃ and mold temperature of 25℃, indicating the simulated grain structure for section A—A and the experimental one, which shows that the simulated result is in agreement with the one obtained experimentally. The mean lengths of columnar grains in Figs.4(a) and (b) are 24mm and 25mm, respectively. And the percent ages of columnar zone are 78% and 80%, respectively.

Fig.4 Comparison of simulated and experimental grain structures of Ti-45%Al alloy ingot for section A—A
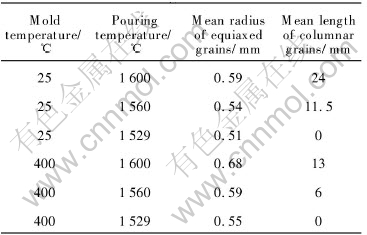
When the mold temperature is 25 and 400℃, pouring temperature changes from 1600℃ to 1529℃, the changes of mean radius of equiaxed grains and mean length of columnar grains are shown in Table 2. For the constant mold temperature, with the increase of pouring temperature, the length of columnar grain increases. Besides, the grain size in the equiaxed zone becomes coarser. This is considered to be mainly caused by the fact that heterogeneous nucleation sites and the amount of undercooling in the bulk liquid decrease with increasing pouring temperature, which postpones the nucleation and growth of equiaxed grains in the liquid ahead of the columnar front. Thus, the CET may not easily occur at higher pouring temperatures. For the constant pouring temperature, with an increase in the mold temperature, the length of the columnar grain decreases. And a coarser structure is achieved in the equiaxed zone. This is due to that an increase in the preheating temperature leads to a lower temperature gradient at the columnar front and a lower cooling rate, so that the tendency to form coarser equiaxed grains increases.
Table 2 Effect of process variables on mean grain size
In this paper, SMA technique is used to minimize the computation time and memory size. The CPU time for the simulation with and without SMA technique is 3.5 and 4h, respectively. By SMA technique, the computation time is reduced 17.5%.
5 CONCLUSIONS
A CA model which accounts for heat transfer, solute diffusion, solute redistribution, grain nucleation and growth is developed to quantitatively predict the solidification grain structures of Ti-45%Al alloy ingot. With the consideration of solidification contraction, the cooling rate is reduced due to the air gap formation. The simulated result for the grain structure is in agreement with the experimental observation. The calculated effect of the process variables upon the resultant grain structures shows that finer structures can be obtained with lower pouring temperature and lower mold temperature. Special moving allocation technique is useful to minimize the computation time and memory size associated with a very large number of cells. The study demonstrates that the present CA model can be applied to predict the solidification grain structures of Ti-Al alloy ingot.
REFERENCES
[1]Ho K S, Kuo J H, Hwang W S. Grain morphology simulation for precision casting of Rene 77 alloy and its experimental verification [J]. AFS Transitions, 2003(111): 1113-1125.
[2]Lipton J, Glicksman M E, Kurz W. Equiaxed dendrite growth in alloys at small supercooling [J]. Metall Trans A, 1987, 18A(2): 341-345.
[3]Wang C Y, Beckermann C. A multiphase solute diffusion model for dendritic alloy solidification [J]. Metall Trans A, 1993, 24A(12): 2787-2802.
[4]Martorano M A, Beckermann C. A soluble interaction mechanism for the columnar-to-equiaxed transition in alloy solidification [J]. Metall Trans A, 2003, 34A(8): 1657-1673.
[5]Spittle J A, Brown S G R. Dynamic simulation of crystal growth by monte carlo method(Ⅱ)—Ingot microstructures [J]. Acta Mater, 1992, 40(12): 3369-3379.
[6]Rappaz M, Gandin C H A. Probabilistic modeling of microstructure formation in solidification processes [J]. Acta Mater, 1993, 41(2): 345-360.
[7]Gandin C H A, Charbon C H, Rappaz M. Stochastic modeling of solidification grain structure [J]. ISIJ Int, 1995, 35(6): 651-657.
[8]WANG Tong-min, JIN Jun-ze, ZHENG Xian-shu, et al. A novel simulation method for the prediction of dendritic grain structures in solidification [J]. International Journal of Cast Metals Research, 2002, 15(4): 231-236.
[9]XU Q Y, Feng W M, Liu B C. Stochastic modeling of dendritic microstructure of aluminum alloy [J]. International Journal of Cast Metals Research, 2002, 15(4): 225-230.
[10]Kim J M, Zhu M F, Hong C P. Evolution of primary phase in solidification of Al-Si alloys [J]. International Journal of Cast Metals Research, 2002, 15(4): 285-289.
[11]ZHU M F, Nishido S, Hong C P. Modeling of eutectic structure formation by a modified cellular automaton model [J]. International Journal of Cast Metals Research, 2002, 15(4): 273-278.
[12]ZHANG L, WANG Y M, ZHANG C B, et al. A cellular automaton model of the transformation from austenite to ferrite in low carbon steels [J]. Modeling and Simulation in Materials Science and Engineering, 2003(11): 791-802.
[13]Lee K Y, Hong C P. Stochastic modeling of solidification grain structures of Al-Cu crystalline ribbons in planar flow casting [J]. ISIJ Int, 1997, 37(1): 38-46.
[14]Cho I S, Hong C P. Modeling of microstructural evolution in squeeze casting of an Al-4.5%Cu alloy [J]. ISIJ Int, 1997, 37(11): 1098-1106.
[15]Lee S Y, Lee S M, Hong C P. Numerical modeling of deflected columnar dendritic grains solidified in a flowing melt and its experimental verification [J]. ISIJ Int, 2000, 40(1): 48-57.
[16]Lee S Y, Lee S M, Hong C P. Numerical simulation of microstructure evolution of Al alloys in centrifugal casting [J]. ISIJ Int, 2001, 41(7): 738-747.
[17]Gandin C H A, Desbiolles J L, Rappaz M, et al. A three-dimensional cellular automaton-finite element model for the prediction of solidification grain structures [J]. Metall Trans A, 1999, 30A(12): 3153-3165.
[18]Kurz W, Giovanola B, Trivedi R. Theory of microstructural development during rapid solidification [J]. Acta Materialla, 1986, 34 (5): 823-830.
[19]Kim S, Grugel R N. The transition from columnar to equiaxed dendritic growth in proeutectic, low-volume fraction copper, Pb-Cu alloys [J]. Metall Trans A, 1992, 23A(6): 1807-1815.
[20]SU Yan-qing, LIU Chang, LI Xin-zhong, et al. Microstructure selection during the directionally peritectic solidification of Ti-Al binary system [J]. Intermetallics, 2005, 13(3-4): 267-274.
Foundation item: Project(50395102) supported by the National Natural Science Foundation of China; Project (JC-02-10) supported by the Distinguished Young Fund of Heilongjiang Province of China
Received date: 2004-11-25; Accepted date: 2005-01-18
Correspondence: WU Shi-ping, Associate Professor, PhD; Tel: +86-451-86418815; E-mail: spwu@hit.edu.cn


