基于支持向量机的预应力T梁压浆质量无损检测
张东风，柳建新，谢维
(中南大学 信息物理工程学院，湖南 长沙，410083)
摘 要：
摘 要：利用超声波透射法对预应力T梁束孔管道的压浆质量进行无损检测，并采用以高斯函数为核函数的支持向量机模式识别技术对检测数据进行自动缺陷识别。在检测过程中，首先采用超声波透射法对T梁的压浆质量进行无损检测，接着建立SVM训练和测试样本库，利用该样本库训练得到SVM模型，最后用该模型对检测数据进行缺陷识别，经对识别结果进行开窗验证。研究结果表明：采用支持向量机算法识别结果准确、可靠；与人工神经网络算法相比，支持向量机算法在训练速度、可靠性等方面都表现出了优越的性能。
关键词：
中图分类号：P315.3 文献标志码：A 文章编号：1672-7207(2010)04-1569-05
Nondestructive testing for grouting quality in prestressed concrete T-beam based on SVM
ZHANG Dong-feng, LIU Jian-xin, XIE Wei
(School of Info-physics and Geomatics Engineering, Central South University, Changsha 410083, China)
Abstract: The characters of ultrasonic wave in an un-grouted beam were tested by ultrasonic pulse-velocity method. The grouting quality of a grouted beam was predicted by support vector machines(SVM). Some testing positions were validated after the experimental test. The results show that the predicting results of SVM are correct, and the grouting quality predict method based on SVM has better performance on the aspects of training speed and reliability than artificial neural network (ANN).
Key words: ultrasonic testing; support vector machines; artificial neural network; T-beam
预应力混凝土T梁作为桥梁的直接承载部位，梁板质量对整个结构来说至关重要[1]。目前，对多跨预制混凝土T梁灌浆管道的压浆质量的检测还没有很好的检测方法。超声波透射法是在检测混凝土缺陷技术的基础上发展起来的一种无损检测手段，现已广泛应用于水利、水电、公路、桥梁等工程检测中。支持向量机(SVM)是近几年在统计学习理论的基础上发展起来的一种新的模式识别方法，它在解决小样本、非线性及高维模式识别问题中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。SVM在字符识别[2]、文本自动分类[3]、人脸检测[4-6]、函数逼近[7-9]、时间序列预测[10]、非线性系统控制[11]等方面得到有效应用。在生物信息学方面，SVM在微阵列数据分析[12]、蛋白质折叠识别[13]、蛋白质交互作用分析[14]、蛋白质亚细胞定位预测[15]、蛋白质二级结构预测[16]等方面均取得了很好的效果。研究表 明[17-18]：支持向量机在许多领域得到比人工神经网络(ANN)方法更优的结果，已大量地用于趋势分析和模式识别以及各种缺陷识别中。为此，本文作者在常吉(湖南常德—吉首)高速公路某大桥预应力T梁束孔管道的压浆质量无损检测中应用超声波透射法，并利用支持向量机技术，对检测数据进行自动缺陷识别，而且对识别结果进行开窗验证，最后与人工神经网络算法自动识别结果进行比较。
1 SVM基本原理
支持向量机的完整的数学描述见文献[19-20]。支持向量的基本思想可用图1进行说明。图1中：实心点和空心点代表2类样本；H为分类线；H1和H2分别为过各类离分类线最近的样本且平行于分类线的直线，它们之间的距离叫做分类间隔。假设训练样本集为(xi, yi)(其中：i=1, …, n；x为输入向量，
Rd；i为样本数；y为输入向量所属的类别，对于2类分类问题，
)，D维空间中线性判别函数的一般形式为
，分类面方程为：
(1)
将判别函数进行归一化，使2类所有样本都满足|g(x)|≥1，即使离分类面最近的样本，其|g(x)|≥1，这样分类间隔就等于
，使间隔最大等价于使
最小。要求分类线对所有样本正确分类，就是要求它满足约束条件：
≥0，i=1, …, n (2)
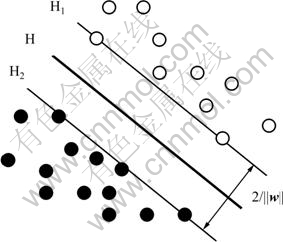
图1 支持向量机的基本思想
Fig.1 Diagram of SVM
考虑到有些训练样本是线性不可分的，Vapnik 等[9]引入非负的松弛变量，将式(2)所示条件放宽为：
≥
，
≥0，i=1, …, n (3)
显然，当划分出现错误时，＞0。因此，在求
分类平面的同时，希望
愈小愈好。所以，原先
对目标函数是求/2的最小值，会变成求目标函数/2+C()的最小值(其中：C＞0，是1个可调
的常数，控制对错分样本惩罚的程度，C越大，表示对错误的惩罚越重)。这是一个二次规划问题，求解这个对偶问题得到最优分类决策函数：
(4)
其中：K(? ,?)为核函数；sgn(?)为符号函数；n为训练样本的数目。
对于线性问题，式(4)中K(? ,?)就是2个向量的点积运算；而对于非线性问题，SVM的核心思想就是通过引入非线性映射
，将输入向量映射到高维空间来构造最优分类面。目前，应用较多的核函数主要有3类：多项式核函数、径向基函数核函数和Sigmoid 函数。
2 声波透射法检测原理及仪器
声波透射法是以弹性波理论为基础，采用由压电材料制成的声-电换能器在不同位置发射和接收声波，测量并记录声波穿透介质所需要的时间和波形，计算声波的传播速度，结合声波幅度、频率等特征来分析介质的性质。当超声波在混凝土中传播时，它将携带有关混凝土材料性能、内部结构及其组成的信息。准确测定这些参数的大小及变化，可以推断混凝土性能、内部结构及其组成情况。
超声波透射法采用的仪器为武汉岩海公司研制的RS-ST01C型非金属声波检测仪，该仪器体积 (长×宽×高)仅为256 mm×264 mm×103 mm，整机质量低于6 kg，它集成了高压脉冲激励、高速信号采集、声参数的自动判读、存储、波形显示、处理、分析、图文打印、数据双向通信等声波测试各种功能。为增强检测时发射信号的强度，获得可靠的透射信号，震源采用由湖南岳阳奥成公司生产的HX-GMM-SV560C型震源系统，该震源具有声波发射能量大、频率高、余振小、转换效率高、使用寿命长等特点，是目前较理想的声波震源之一。
3 SVM缺陷自动识别结果
3.1 SVM训练和测试样本库的建立
由于支持向量机法是根据训练样本来选择特征参数，建立判别函数自动识别缺陷的，因此，首先要在已知、未灌浆的梁上进行测试，并将该测试成果作为训练样本集。某大桥4-14边梁波纹管内还未压浆，因此，波纹管内明显存在空洞，在经过钢束位置测得的波速表示经过空隙位置时的检测波速，将其作为缺陷样本，而以不过钢束位置测得的速度(相当于波纹管内无空隙时的波速)作为正常混凝土样本。
表1所示为常吉高速公路某大桥4-14边梁上的部分检测结果，将混凝土厚度、速度、振幅、主频作为特征向量组成SVM训练样本集。其中：位置(x坐标)表示检测点在T梁上的水平位置，x=0表示位于T梁的中心，x为负数表示检测点位于梁的西面，正号则表示检测点在梁的东面，单位为m；类别为0表示缺陷样本，类别为1表示正常混凝土样本。
表2所示为超声透射法在(已压浆)边梁左7-a1上的部分检测结果，同样将混凝土厚度、速度、振幅、主频作为特征向量组成SVM测试样本集。其中，检测点的纵坐标位置在备注栏中说明，如：“N1”表示检测点在纵向高度上正对N1钢束，其具体高度由设计图纸可知。
表1 SVM训练样本集
Table 1 SVM samples
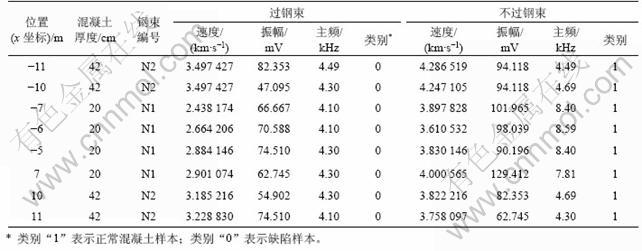
表2 边梁左7-a1超声波透射检测结果、SVM及ANN识别检测结果
Table 2 Results tested by ultrasonic pulse-velocity method SVM and ANN for side beam 7-a1
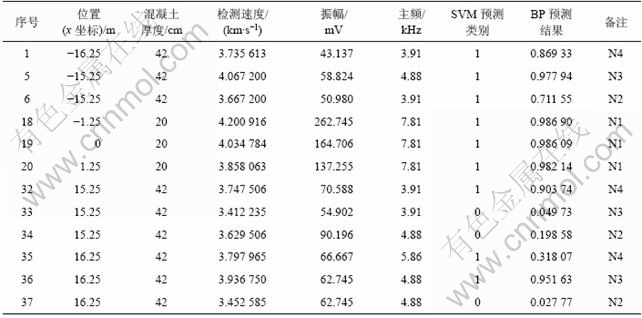
建立好训练和测试样本库后，应用SVM算法进行缺陷自动识别的关键问题就是选择合适的核函数参数和误差惩罚因子C。统计学理论目前对这些问题给出了一些建议和解释，但还没有给出实际可行的方案，Vapnik等[9]的研究表明：SVM的性能与所选用的核函数的类型关系不大，而核函数的参数和误差惩罚因子C是影响SVM性能的主要因素。因此，本文作者在设计SVM分类器时，选择RBF函数作为核函数，而对于RBF，需要选择的参数只有核参数γ和惩罚因子C。本文采用交叉比对算法(Cross-validation)来选取这2个参数。交叉比对法的过程是：将样本集分成n个子集，每次将其中n-1个子集代入SVM训练，针对SVM的惩罚因子C和不同的核函数，计算剩余1个子集的分类正确率。系统根据误差自动调整惩罚因子C的取值。n的取值一般为10。通过上述实验得到最佳SVM模型，最后应用该模型对提取的测试样本进行缺陷自动识别，识别结果见表2(其中：“0”表示缺陷样本，“1”表示正常混凝土样本)。图2所示为测试点的位置及最终得到的测试结果。从测试点所处的区域可以明显看出样本所属的类别。
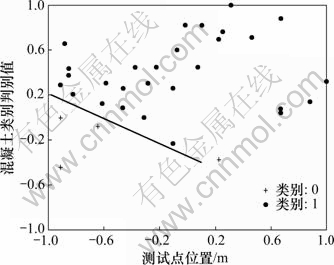
图2 测试点位置及测试结果
Fig.2 Test results at different positions
3.3 SVM与ANN的测试结果比较
杨天春等[21]利用ANN方法对同组数据进行缺陷自动识别，结果见表2。从SVM和ANN的缺陷自动识别结果对比可以看出：从识别结果中检测点22，33，34和37的波纹管中可能存在压浆不密实问题。先后对检测点20和33进行现场开窗检验，发现33号检测点压浆不密实，存在明显的空隙；20号检测点有充分压浆。说明SVM识别精度与实际情况较吻合，SVM识别结果与ANN结果相近，但基于SVM方法缺陷自动识别具有以下特点：
(1) 训练与识别速度快。在网络结构不是很复杂的情况下，BP网络的训练过程用时10.263 s，而支持向量机的训练时间仅为0.092 s。
(2) 训练和识别过程比较稳定。在实验过程中，神经网络的训练过程很不稳定，识别结果也随之变化。而支持向量机在训练和识别过程中比较稳定，训练时间较短。
4 结论
(1) 将SVM 缺陷自动识别方法用于T梁压浆质量无损检测中，并对识别结果进行验证。该方法克服了传统缺陷检测中通过使用仪器检测来识别缺陷所具有的工序繁琐、不易在线实施、受人为因素影响等弊端，对于T梁压浆质量进行无损检测。与人工神经网络相比，支持向量机在训练速度、可靠性等方面都表现出优越的性能。
(2) 需指出的是：这项技术目前只能对缺陷的有无进行自动识别，而对于缺陷的大小、形状等更为复杂情形的识别，还有待于进一步研究。
参考文献：
[1] 姚向红. 预应力砼T梁预制施工的质量控制[J]. 山西交通科技, 2003, 158(4): 67-68.
YAO Xiang-hong. The quality control of prestress concrete T beam precast construction[J]. Shanxi Science & Technology of Communications, 2003, 158(4): 67-68.
[2] Scholkopf B, Sung K, Burges C, et al. Comparing support vector machines with Gaussian kernels to radial basis function classifiers[C]//IEEE Transactions on Signal Processing. Paris, 1997: 2758-2765.
[3] Joachims T. Text categorization with support vector machines: Learning with many relevant features[C]//Nedellec C, Rouveirol C. Proceedings of the Tenth European Conference on Machine Learning (ECML '98). Berlin: Springer-Verlag, 1998: 137-142.
[4] Osuna E, Freund R, Girosi F. Training support vector machines: An application to, face detection[C]//Proceedings of the 1997 Computer Vision and Pattern Recognition (CVPR'97). Puerto Rico, 1997(2): 130-136.
[5] Jonsson K, Matas J, Kittler J, et al. Learning support vectors for face verification and recognition[C]//Crowley J. Proceedings of Fourth IEEE International Conference on Automatic Face and Gesture Recognition 2000. Grenoble, France, 2000(4): 208-213.
[6] Kumar V, Poggio T. Learning-based approach to real time tracking and analysis of faces[C]//Crowley J. Proceedings of Fourth IEEE International Conference on Automatic Face and Gesture Recognition 2000. Grenoble, France, 2000(3): 96-101.
[7] Smola A J, Scholkopf B. A tutorial on support vector regression[J]. Statistics and computing, 2004, 14(2): 199-222.
[8] 田盛丰, 黄厚宽. 基于支持向量机的数据库学习算法[J]. 计算机研究与发展, 2000, 37(1): 17-22.
TIAN Sheng-feng, HUANG Hou-kuan. Database learning algorithm based on support vectormath[J]. Journal of Computer Researth and Development, 2000, 37(1): 17-22.
[9] Vapnik V, Golowich S, Smola A. Support vector method for function approximation, regression estimation, and signal processing[C]//Mozer M, Jordan M, Petsche T. Neural Information Processing Systems 9. Cambridge, MA: MIT Press, 1997(4): 281-287.
[10] Miller K R, Smola A J, Ratsch G, et al. Predicting time series with support vector machines[C]//Gerstuner W, Germond A, Hasler M, et al. Artiificial Neural Networks(ICANN'97). Berlin: Springer-Verlag, 1997: 999-1004.
[11] Suykens J A K, Vandewalle J, De Moor B. Optimal control by least squares support vector machines[J]. Neural Networks, 2001, 14(1): 23-25.
[12] Furey T S, Cristianini N, Duff N, et al. Support vector machine classification and validation of cancer tissue samples using microarray expression data[J]. Bioinformatics, 2000, 16(3): 906-914.
[13] Dubchak I, Muchnik I, Mayor C, et al. Recognition of a protein fold in the context of the SCOP classification[J]. Proteins: Structcture, Function and Genetics, 1999, 35(3): 401-407.
[14] Bock J R, Gough, D A. Predicting protein-protein interactions from primary structure[J]. Bioinformatics, 2001, 17(8): 455-460.
[15] Cai Y D, Liu X J, Xu X B, et al. Support vector machines for prediction of protein subcellular location by incorporating quasi-sequence-order effect[J]. Journal of Cellular Biochemistry, 2002, 84(11): 343-348.
[16] Hua S, Sun Z. A novel method of protein secondary structure prediction with high segment overlap measure: Support vector machine approach[J]. Journal of Molecular Biology, 2001, 308(2): 397-407.
[17] 张金泽, 单甘霖. SVM技术与ANN方法对旋转机械故障诊断性能的比较[J]. 电光与控制, 2006, 13(3): 72-74.
ZHANG Jin-ze, SHAN Gan-lin. Comparison of fault diagnosis performances based on SVM and ANN[J]. Electronics Optics & Control, 2006, 13(3): 72-74.
[18] 柴月君, 杨万麟. 基于BP网络和支持向量机的雷达高分辨距离像识别[J]. 现代电子技术, 2006, 228(13): 15-17.
CHAI Yue-jun, YANG Wan-lin. High resolution range profile identification of radar based on SVM and BP network[J]. Modern Electronics Technique, 2006, 228(13): 15-17.
[19] Vapnik V N. The nature of statistical learning theory[M]. New York: Springer Verlag, 1995: 20-24.
[20] Vapnik V N. Statistical learning theory[M]. New York: Wiley, 1998: 18-30.
[21] 杨天春, 易伟建, 鲁光银, 等. 预应力T梁束孔管道压浆质量的无损检测试验研究[J]. 振动工程学报, 2006, 19(3): 411-415.
YANG Tian-chun, YI Wei-jian, LU Guang-yin, et al. Experimental study of nondestructive testing for grouting quality in prestressed concrete T-beam[J]. Journal of Vibration Engineering, 2006, 19(3): 411-415.
收稿日期：2009-11-25；修回日期：2010-03-05
基金项目：国家自然科学基金资助项目(60672042)
通信作者：张东风(1964-)，男，山西太原人，博士研究生，从事电磁场理论，正反演计算及其相关应用研究；电话：13703580368；E-mail: zhangdongfeng220@126.com
