中南大学学报(英文版)

J. Cent. South Univ. Technol. (2011) 18: 1144-1152

DOI: 10.1007/s11771-011-0816-1

Survivability modeling and analysis on 3D mobile ad-hoc networks

PENG San-cheng(彭三城)^{1, 2}, WANG Guo-jun(王国军)², HU Zhong-wang(胡忠望)¹, CHEN Jian-ping(陈建平)¹

1. School of Computer Science, Zhaoqing University, Zhaoqing 526061, China;

2. School of Information Science and Engineering, Central South University, Changsha 410083, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Key words:

mobile ad-hoc networks (MANETs); survivability; node behaviors; semi-Markov process; network connectivity；

1 Introduction

Three dimensional (3D) networks, particularly 3D mobile ad-hoc networks (MANETs) [1] and 3D wireless sensor networks (WSNs), have many applications [2-5]. For example, an air force which employs unmanned aerial vehicles deploys MANETs in 3D space to construct defense systems for surveillance of airspace; a navy can use underwater autonomous vehicles to form a 3D network for ocean surveillance; meteorologists use balloons to build 3D pollution monitoring systems for aerosphere surveillance.

Survivability [6-7] is an essential aspect of reliable communication services. Usually, it is defined as the capability of a system to fulfill its mission, in a timely manner, in the presence of accidents, failures, or attacks. To establish a highly survivable system, it is necessary to measure its survivability to evaluate the performance of the services of the system under adverse conditions. Moreover, it is a critical issue to improve the availability in real networks.

Compared with the traditional networks, MANETs are more vulnerable to various failures as well as attacks due to their characteristics, such as dynamic network topology, restricted power supply, limited computational capabilities, and continuously changing scale.

In this work, the focus was put on survivability modeling and analysis in 3D MANETs. In particular, the focus was put on the following problem: How can we model and analyze the survivability in 3D MANETs whether or not there are at least k node-disjoint paths between any pair of nodes in the presence of node misbehaviors?

This problem is fundamental in 3D MANETs. Solving this problem has both theoretical and practical significances. First, survivability is very important to ensure that end users obtain necessary services and to construct a reliable network. Second, if a 3D mobile ad-hoc network is k-connected, it is possible to examine the survivable degree in practical 3D environments. Third, quantitative evaluation for survivability can also provide guidance for designing topology control algorithms in 3D MANETs.

However, the above problem is hard to answer with existing approaches. It is noticed that in Refs.[6-7] network survivability has been defined from different perspectives, which provides a general intuitive notion of survivability and is applicable for traditional telecommunication networks, not for MANETs.

It is also noticed that network connectivity has been used as a metric in evaluating the survivability of ad-hoc networks [7]. In addition, extensive efforts have been made on asymptotic connectivity of MANETs [8-9]. In these works, a common premise is that as long as a node has active neighbors, the node is connected to the network “physically” via wireless links. Nevertheless, the premise can hardly be held in real networks if potential node misbehaviors are taken into account.

For example, selfish nodes may not forward control and/or data packets for other nodes for the sake of saving their own energy, and malicious nodes may launch denial of service (DoS) attacks, such as black hole, to interrupt the normal routing process. A lot of work has been found to characterize various node misbehaviors and evaluate their effects on network performance [10-12]. However, little research has been done on the survivability modeling and analysis caused by node misbehaviors in 3D MANETs.

The continuous time Markov chain (CTMC) has been proposed by CHEN et al [13] to represent a connection availability model for a two hop ad-hoc network that incorporates the physical faults such as node, power, and link faults, without considering a variety of other faults and connection states for mobile terminals. A quantitative approach has been proposed by KOROMA and LI [14] to evaluate the network survivability by using a generalized model, and a more complex system has been considered with multiple faults to analyze the network survivability by using CTMC based on Ref.[13]. A model which considers various types of faults and connection states of mobile hosts has been proposed, and CTMC has been used to describe the survivability of MANETs in a precise manner by PENG et al [15]. Moreover, the reliability theory has been introduced to perform quantitative analysis and evaluation of survivability in large-scale MANETs. A model based upon semi-Markov process (SMP) [16] has been proposed by XING and WANG [17] to characterize the evolution of node behaviors, and to analyze the survivability of wireless ad-hoc networks by examining the cooperative degree and the probabilistic k-connectivity of individual nodes.

Survivability modeling and analysis require reasonable analysis on network connectivity based on node behaviors. However, little work has been done on how node misbehaviors affect survivability in 3D MANETs. Following the probabilistic flavor of Ref.[8], but applying the semi-Markov model of node behaviors pertaining to 3D MANETs, node isolation to network connectivity is investigated in this work from two-dimensional scenarios to three-dimensional ones.

2 Network model

To model and analyze the survivability in 3D MANETs, it is assumed that network model has the following natures:

1) All nodes have identical transmission radius r, and use omnidirectional antennas. Any pair of nodes is able to communicate directly via a wireless link, if they are within the range of each other. The communication region of each node can be represented by a sphere of radius r, with the node at its center.

2) The transmission radius r is much smaller than the length, the width, or the height of 3D space to be covered, so that the border effect is negligible and hence can be eliminated.

3) Any point in 3D space to be covered must be within the communication range from at least one node.

Thus, the underlying communication graph of a mobile ad-hoc network is modeled by a geometric random graph G(N, r) [18-20], where N denotes the vertex set, and an edge exists between two vertices in the graph only if their distances are not greater than r.

3 Node behavior modeling

3.1 Utilization for semi-Markov process (SMP)

Simple Markov chain is difficult to estimate the misbehaviors of nodes. The reasons are described as follows.

1) The transition time from one state to another is based on random behaviors of node.

2) It is very difficult to characterize the transition time by exponential distributions. For instance, a node is more inclined to fail due to energy consumption as time passes, and the less the residual energy is left, the more likely the node changes its behavior to be selfish.

3) System responses to the attacks, which causes the sojourn time of some states to be non-exponential. The future action of a node may depend on how long it has been in the current state and transition intervals may have arbitrary distributions.

Thus, the simple Markov chain will not be used to describe node behaviors, especially in the presence of node misbehaviors. In this work, the SMP is used to characterize the transition of node behaviors.

3.2 Classification of node behaviors

According to the node property of MANETs, node behaviors are divided as follows.

Healthy behavior (H): Nodes are active in route discovery and packet forwarding, but not in launching attacks.

Selfish behavior (S): Nodes can initiate and respond route discovery for its own purpose, but they may not forward packets for others due to energy saving.

Malicious behavior (M): Nodes are active both in route discovery and attacks launching, e.g., black hole attack, and gray hole attack.

Failed behavior (F): Nodes are not active in route discovery and packet forwarding.

In this work, two types of malicious behaviors are emphasized: black hole and gray hole attacks [21]. Black hole attack indicates that a malicious node, called black hole node, always claims itself as having the shortest path to destination by sending forged routing packets. The attacker can cause all packets for the destination to be routed to itself and can then discard them, or the attacker can cause the route at all nodes in an area of the network to point “into” that area when in fact the destination is far from the area. Gray hole attack is referred to as a special case of black hole attack. In this attack, the attacker selectively drops packets. For example, the attacker may forward routing packets, but not data packets.

3.3 Model of node behaviors

A node may change its behaviors as follows.

1) A healthy node becomes failed due to many reasons, e.g., energy exhaustion, and hardware faults. It is also prone to be configured on purpose as a selfish node for the sake of energy saving, or to be compromised as a black/gray hole node.

2) A selfish node can become healthy again by means of proper configurations, and can also become a black/gray hole node due to being compromised.

3) A black/gray hole node can become a failed node, but it will not be considered to be healthy or selfish any more.

4) A failed node can become healthy again if it is recovered and responds to routing operations.

The above assumptions are simple enough to model node behaviors in an exact mathematical method, which is presented as follows.

1) Let the transitions of the process {X(t), t≥0} occur at epochs (or instants of times) t₀, t₁, …, t_n, with  t₀<>₁<…<>_n.

2) Let Z_n denote the state of the system at epoch t_n such that the Markov property is satisfied at each time epoch t_n.

3) The pair {X_n, t_n} constitutes a Markov renewal sequence on state space E={H (healthy), S (selfish), B (black hole), G(gray hole), F (failed)}.

4) Note that {Z_n, n=0, 1, …} constitutes a discrete time Markov chain (DTMC) with state space E. Thus, the stochastic process {X(t), t≥0} is a SMP, where

                  (1)

Here, the Markov chain {Z_n, n=0, 1, …} is said to be an embedded discrete time Markov chain (DTMC) of the SMP {X(t), t≥0}. The transition probability matrix of {Z_n} is given by

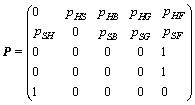                      (2)

where p_ii=0 denotes that {Z_n} only has transitions from a state to another different state. In Eq.(2), a transition probability of 0, such as p_BH=0 or p_BS=0 means that black hole node will not become healthy or selfish. Moreover, since the summation of transition probabilities to a state must be equal to 1 in a stochastic matrix, the conclusion can be p_BF=1 or p_GF=1, etc.

The transition from one state to another in a SMP can be presented by two matrices, P=(p_ij) and F(t)= (F_ij(t)), where p_ij is the transition probability of node behaviors from state i to state j, while F_ij(t) is the distribution function of time spent from state i to j. The model of node behaviors is shown in Fig.1.

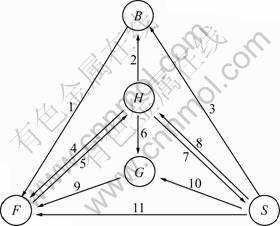
Fig.1 Semi-Markov process for node behavior: 1—p_BF, F_BF(t); 2—p_HB, F_HB(t); 3—p_SB, F_SB(t); 4—p_HF, F_HF(t); 5—p_FH, F_FH(t); 6—p_HG, F_HG(t); 7—p_HS, F_HS(t); 8—p_SH, F_SH(t); 9—p_GF, F_GF(t); 10—p_SG, F_SG(t); 11—p_SF, F_SF(t)

The SMP model defined above enables us to consider the evolution process of node behaviors without the assumption of memoryless property. Additionally, this model can be used to describe a wide variety of random threats, caused by node misbehaviors, which depend on how to diffuse data into it. Specifically, let T_n=t_n+1-t_n be the sojourn time between n-th and (n+1)-th transition, and then the associated (time-homogeneous) semi-Markov kernel Q=(Q_ij(t)) can be defined by

                   (3)

where p_ij is the transition probability between states i and j, and F_ij(t) is the transition probability of {Z_n}.

 

To analyze an SMP, three sets of parameters are to be dealt with: 1) mean sojourn time M(i) in state iE, 2) the transition probabilities p(i, j) between different states i, jE, and 3) M(i, j) that denotes the mean transition time from state i to j.

Let T_i be the sojourn time in state i, and T_ij be the transition time from states i to j, then the mean sojourn times are expressed by

Theorem 1: Given SMP {X(t), t≥0} associating with state space E, and DTMC defined by Eq.(3), the transient distribution P_ij(t) converges to a limiting probability P_j as t→∞; further, P_j can be calculated as

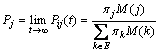                                (4)

Proof: Let T_j(i) denote the sojourn time in state Z_j for the i-th time (i, j≥0), and the N_j(k) denote the arrival times at state Z_j among the previous k times of transition in semi-Markov process. Thus, the time ratio of the arrival times can be obtained at state Z_j among the previous k times of transition as

          (5)

When k→∞, N_j(k)→∞, by the strong law of large numbers, the following equation is obtained:

                                          (6)

Let u denote the number of transitions between the two arrivals at state j. By the central limit theorem of a renewal process, the following equation is also obtained:

                                       (7)

Thus, let k→∞ in Eq.(5), Eq.(4) is obtained. This proves the theorem.

To calculate P_j, we only need to estimate p_ij and M(i, j), which are normally easier to obtain from the

statistics. Then,  and  are used to calculate π_i and M(i, j).

4 Network connectivity and node isolation

4.1 Isolated node and minimum node degree

Proposition 1: Suppose that the number of points, denoted by random variable  are randomly distributed on a 3D space Λ with volume |Λ|, and that X_Λ satisfies Poisson distribution, denoted by X_Λ~Poisson_a|Λ| (a is a positive constant), and that the distance between a chosen point and its nearest neighbor is η, where η obeys Weibull PDF [22] (Distribution function of η is F_η(x)= 1-exp(-4πax³/3)).

Proof: The derivation of distribution function F_η(x) is given by f(η)=(F_η(x))′=4πax²exp(-4πax³/3). Let σ=a=3, λ=4π, f(η)=λση^σ-1exp(-λη^σ) can be obtained (σ, η>0). By Weibull distribution, W(σ, λ), f(η)=λση^σ-1exp(-λη^σ) obeys this distribution. This completes the proof.

This work starts reviewing some results on the connectivity of geometric random graphs, as derived by BETTSTETTER [8]. It is assumed that the nodes are distributed according to a 3D Poisson point process, with a set of N nodes, each of which with a transmission range r, is randomly uniformly placed in a large volume V>>4πr³/3. Then, node density is δ=N/V.

By Proposition 1, one of the key properties of this kind of point process is that the probability density function (PDF) of the distance between a node and its nearest neighbor is a Weibull PDF. The distance between one node and its nearest neighbor is denoted as its nearest neighbor distance η. Thus, for a homogeneous Poisson point process in 3D network, the PDF of the nearest neighbor distance is f(η)=4πδη²exp(-4πδη³/3) (η>0).

Definition 1: The degree of a node i, denoted d(i), is the number of neighbors of node i, i.e., its number of links.

Definition 2: The minimum node degree of a graph

G is denoted

In 3D MANETs, the probability of the distance between a randomly chosen node to its nearest neighboring node is less than or equal to r:

       (8)

The probability that a node has no neighbor (i.e., it is isolated) is

By Definition 1, if d(i)=0, node i has no neighbors, that is, it is isolated. Our aim is to achieve the probability of a network graph G in which none of the N nodes is isolated, i.e., if d(i)>0,  Assuming statistical independence, the probability for this event is

Let N_T denote the number of neighbors of node i. For a given density δ, the probability that m nodes are in

a volume V₀ is

By δ=N/V and V₀=4πr³/3, the probability that a randomly chosen node has m neighbors can be obtained

by

Thus, given a 3D MANET with N>>1 nodes, the probability that each node has at least m neighbors, i.e., the network has a minimum node degree d_min>m, is given by

 (9)

4.2 Modeling on node isolation problem

Definition 3: Node isolation means that a node i has at least one black/gray hole neighbor or the total number of its neighbors is selfish and/or failed.

Definition 4: Node-disjoint outgoing path [11] is the path through which a node can communicate with the nodes of at least two hops away.

The study of node isolation problem starts by analyzing the following three cases.

1) Impact from selfish behavior of neighboring nodes

In Fig.2, suppose node A₃ is a selfish node. When node S initiates a route discovery to node D, the selfish neighbor A₃ may be reluctant to broadcast the route request from S. In this case, A₃ behaves like a failed node. It is also possible for A₃ to forward control packets; however, the situation could be worse since S may select A₃ as the next hop and send data to A₃. Thus, A₃ may discard all the data to be forwarded via itself, then, communications between S and D cannot proceed. If all neighbors of S are selfish, S is unable to establish any communication with other nodes at a distance of more than one-hop away. In this case, a node is isolated by its selfish neighbors.

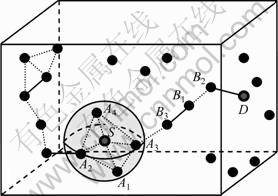
Fig.2 Node isolation due to failed or selfish neighbors

2) Impact from failed behavior of neighboring nodes

In Fig.2, suppose node A₃ is a failed node. When node S initiates a route discovery to another node D, the failed neighbor A₃ is unable to forward the route request packets. If all neighbors of S are failed, S cannot communicate with other nodes. In this case, S is isolated by its failed neighbors.

3) Impact from black/gray hole behavior of neighboring nodes

In Fig.3, suppose node A₄ is a black/gray hole node. When node S discovers the route to node D by broadcasting RREQ messages, A₄ can respond S with a fake RREP message by immediately claiming that it is in the optimal path or only one-hop away from node D. Thus, S selects A₄ as the next hop and sends data to A₄, but A₄ will just drop all packets. S will eventually lose communications with the nodes at least two hops away. Moreover, the black hole node may be able to trap all traffics of its neighbors, which implies multiple node isolations in the worst case.

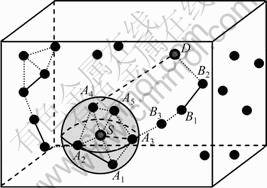
Fig.3 Node isolation due to black/gray hole neighbors

Let N_P(i) denote the number of node-disjoint outgoing paths of node i. Figure 2 shows the scenario where all the neighbors of node S are selfish nodes. In this case, N_P(S)=0. Figure 3 shows that A₄ is a black/gray hole neighbor of node S. In fact, only one black hole neighbor A₄ is sufficient to trap all traffic initiated from node S if the destination is beyond the neighborhood of node S. In this case, N_P(S)=0.

Let N_H, N_B, N_G, N_F, and N_O denote healthy, black hole, gray hole, failed, and other neighbors, respectively. By Definition 3, the probability of a node being isolated can be obtained, given that the node has m neighbors, is defined as

            (10)

where P_B, P_G and P_H denote the probabilities that a node is healthy, a black hole, and a gray hole, respectively; 1-P_B-P_G denotes the probability of a node being neither a black hole nor gray hole; 1-P_H-P_B-P_G denotes the probability of a node being neither healthy, nor a black hole, nor a gray hole. Thus, to keep a node connecting to the network, it must have at least one healthy and no black/gray hole neighbor at the same time.

4.3 3D connectivity

The probabilistic connectivity of individual nodes is derived based on the model of node isolation.

Let K(G′) denote k-connectivity of a graph G′. Then, it is well known that K(G′)≤d_min(G′) [8], which implies that the connectivity of a network is no greater than the minimum number of neighbors of any node.

Lemma 1: For a geometric random graph G′ with N vertices, the probability that G′ is k-connected approximately is equal to the probability that every vertex has at least k neighbors [8]:

     (11)

If border effects are eliminated, by Eqs.(9) and (10), the probability P(G′ is k-connected) is given by

            (12)

According to Definition 3, it is known that a node i has k node-disjoint outgoing paths if and only if i has k healthy neighbors and no black/gray hole neighbors. Thus,  is obtained, which may be simplified by   Notice that the events of any node being in a certain behavior state are mutually independent, then, by multinomial probability law and Lemma 1, the probability of a node being k-connected in the network, given that the node has m neighbors, is defined as

                          (13)

5 Survivability computing

After modeling the evolution of node behaviors by the SMP and analyzing the effect of node misbehaviors on the connectivity of individual nodes, how to compute the survivability of MANETs in a closed form is presented by using theoretical analysis in the presence of node misbehaviors.

By Lemma 1, a network G is connected if and only if any active node i of G has at least k node-disjoint outgoing paths or has at least k healthy neighbors. Thus, the network survivability is represented by the probability of G being k-connected:

                  (14)

where (1-P(N_H

      (15)

Since the number of healthy neighbors of node i cannot be greater than its total number of neighbors, it gets to

             (16)

When k>m, P(N_H<>_T=m)=1; when k≤m, it is described by Eq.(16). Thus, P(N_H<>_T=m) is given by

 

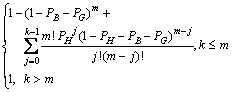   (17)

When the number of nodes N and the communication domain V are sufficiently large, the probability that a randomly chosen node has m active neighbors is obtained as

                                 (18)

where

Thus, by Eqs.(15), (17), and (18), P(N_H

 

 (19)

The computation procedure on Eq.(19) is described as follows.

1) The first item on the right side of Eq.(19) is given by

                                         (20)

2) The second item on the right side of Eq.(19) is given by

 (21)

Let

Thus, Eq.(21) is simplified as

   (22)

3) In the same way, the third item on the right side of Eq.(19) is given by

 (23)

Thus, by Eqs.(20), (22), and (23), P(N_H

  (24)

Finally, by Eqs.(14) and (24), S(G) is given by

  (25)

By Eq.(25), the impact of different node behaviors on survivability can be quantified directly.

6 Numerical validation

The correctness and rationality of Eq.(25) on the survivability analysis in 3D MANETs is verified. The related parameters are listed as follows. The communication range Ω is 10⁹ m³, the number of nodes N is 250, and transmission radius r is 250 m.

The survivability analysis in 3D MANETs is considered from the following six cases.

1) The effect on survivability from healthy probability P_H

To observe the effect of healthy probability clearly, P_B + P_G = 0 is set so that P_H varies only due to node selfishness attack and node failure. Let P_F = 0.03 so as to highlight the effect of node failures due to the mobility or faults. Figure 4 shows the analytic results of survivability under the probability of k-connectivity against P_H for k=1, 2, 3, 4, respectively. To obtain a higher survivability, it is necessary to have a higher healthy probability P_H.

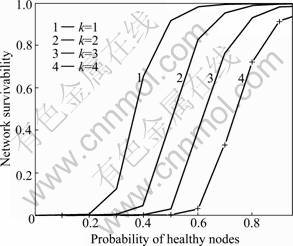
Fig.4 Effect on survivability from healthy probability P_H of node health

2) The effect on survivability from probability of node failures P_F

To explain the effect of node failures on network survivability, it is set that P_B+P_G=0, P_S=0 to eliminate the effect of misbehaving nodes in simulations. From Fig.5, the survivability decreases very fast as P_F increases. As it is expected, for a highly survivable network, the effect of P_F is more significant, e.g., the survivability drops to 0.1 as P_F=0.3 and k=3. Therefore, the probability of node failures cannot be ignored for a more survivable network.

3) Effect on survivability from probability of node selfishness P_S

In the same way, let P_B+P_G=0, P_F=0.03, and then the results can be obtained from selfish nodes in Fig.6. Similar to that in Fig.4, the plot in Fig.6 shows that the survivability decreases as selfish probability P_S increases. Nevertheless, different from the results in Fig.4, the survivability does not change significantly when P_S increases at the beginning, especially for lower k. Notice that the number of active nodes N_A decreases as P_F increases, which makes the network sparser in terms of decreased node density (e.g., ρ=N_A/V if the node distribution is uniform). Thus, the partitioning effects of node failures are severer than those of selfish nodes.

Fig.5 Effect on survivability from probability P_F of node failures

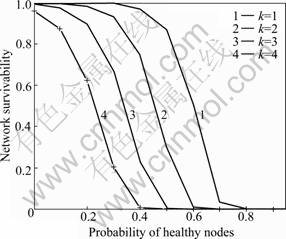
Fig.6 Effect on survivability from probability P_S of node selfishness

4) Effect on survivability from the probability of black/gray hole P_B+P_G

To explain the effect of node selfishness on survivability, here the effect of black/gray hole with the probability of P_B+P_G can be known. By Eq.(25), P_B+P_G has tremendous influence on the survivability. Analytical results are illustrated in Fig.7, from which black/gray hole behavior is more harmful on network survivability than node failures do. Recalling the node isolation problem discussed before, it can be found that a black/gray hole actually can isolate all its neighbors, and that its influential scope will be extended when it roams in the whole network.

In addition to node behaviors, the effects of other system parameters on network survivability are also evaluated in this work.

5) Effect on survivability from transmission radius r of node

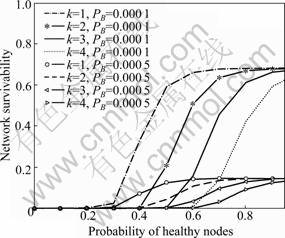
Fig.7 Effect on survivability from probability P_B of black hole

To discuss the effect of the transmission radius r of the node on survivability, let P_H=0.8, P_F=0.2, and the transmission radius r is changed from 300 to 100 m. From Fig.8, it is known that the larger the r value is, the stronger the survivability.

6) Effect of network size N on survivability

In the same way, let P_B=0, P_F=0.2, and then the results are obtained from the network size N in Fig.9. The plot in this figure shows that the survivability decreases as the network size N increases, and also shows that the density of node has influence on the network survivability.

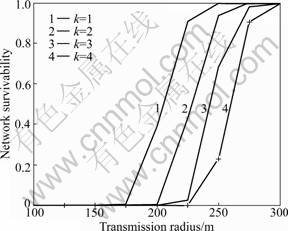
Fig.8 Effect on survivability over transmission radius r of node (P_H=0.8, P_F=0.2)

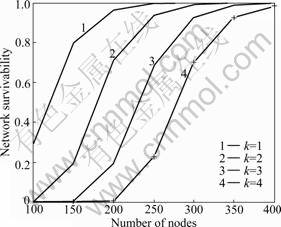
Fig.9 Effect on survivability over network size N (P_H=0.8, P_F= 0.2)

7 Conclusions

1) The survivability modeling and analysis on 3D MANETs are investigated. The impact of node misbehaviors on network survivability can be quantified. The results show that node misbehaviors can seriously affect the survivability of MANETs.

2) To the best of our knowledge, this work makes the attempt towards a quantitative analysis approach to analyze the survivability of 3D MANETs. The results in this work provide technical guidelines on building fault-tolerant and robust topology to improve network survivability.

3) As future work, further improvements on the method of modeling for survivability and node behaviors of state transition graph on survivability are to be made, and the parameters of network performance will also be analyzed, such as throughput, QoS and transmission delay.

References

[1] PENG San-cheng, JIA Wei-jia, WANG Guo-jun, WU Jie, GUO Min-yi. Trusted routing based on dynamic trust mechanism in mobile ad-hoc networks [J]. IEICE Transactions on Information and Systems, 2010, E93-D(3): 510-517.

[2] HEIDEMANN J, YE Wei, WILLS J, SYED A, LI Yuan. Research challenges and applications for underwater sensor networking [C]// Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC 2006). Las Vegas, Nevada, USA, IEEE Computer Society, 2006: 228-235.

[3] ALAM S M N, HAAS Z J. Coverage and connectivity in three-dimensional networks [C]// Proceedings of the Eighth Annual International Conference on Mobile Computing and Networking (MobiCom 2006). Los Angeles, California, USA, IEEE Computer Society, 2006: 346-357.

[4] BAI Xiao-le, ZHANG Chuan-lin, XUAN Dong, JIA Wei-jia. Full-coverage and k-connectivity (k=14, 6) three dimensional networks [C]// Proceedings of the 28th IEEE International Conference on Computer Communications (INFOCOM 2009). Rio de Janeiro, Brazil, IEEE Computer Society, 2009: 388-396.

[5] LIU Cong, WU Jie. Efficient geometric routing in three dimensional ad hoc networks [C]// Proceedings of the 28th IEEE International Conference on Computer Communications (INFOCOM 2009). Rio de Janeiro, Brazil, IEEE Computer Society, 2009: 2751-2755.

[6] LIMA M N, SANTOS A, PUJOLLE G. A survey of survivability in mobile ad hoc networks [J]. IEEE Communications Surveys & Tutorials, 2009, 11(1): 66-77.

[7] KAWAHIGASHI H, TERASHIMA Y, MIYAUCHI N, NAKAKAWAJI T. Designing fault tolerant ad hoc networks [C]// Proceedings of IEEE/AFCEA Military Communications Conference (MILCOM 2005). Atlantic City, New Jersey, IEEE Computer Society, 2005: 1360-1367.

[8] BETTSTETTER C. On the minimum node degree and connectivity of a wireless multihop Network [C]// Proceedings of the 3rd ACM International Symposium On Mobile Ad Hoc Networking and Computing (MobiHoc 2002). Lausanne, Switzerland: ACM, 2002: 80-91.

[9] SANTI P. The critical transmitting range for connectivity in mobile Ad Hoc networks [J]. IEEE Transaction on Mobile Computing, 2005, 4(3): 310-317.

[10] HOLLICK M, SCHMITT J, SEIPL C, STEINMETZ R. On the effect of node misbehavior in ad hoc networks [C]// Proceedings of the IEEE International Conference on Communications (ICC 2004). Paris: IEEE Computer Society, 2004: 3759-3763.

[11] XING Fei, WANG Wen-ye. Modeling and analysis of connectivity in mobile ad hoc networks with misbehaving nodes [C]// Proceedings of the IEEE International Conference on Communications (ICC 2006). Istanbul, Turkey: IEEE Computer Society, 2006: 1879-1884.

[12] KOMATHY K, NARAYANASAMY P. A probabilistic behavioral model for selfish neighbors in a wireless ad hoc network [J]. International Journal of Computer Science and Network Security, 2007, 7(7): 77-83.

[13] CHEN Dong-yan, GARG S, TRIVEDI K S. Network survivability performance evaluation: A quantitative approach with applications in wireless ad-hoc networks [C]// Proceedings of the 5th ACM International Workshop on Modeling Analysis and Simulation of Wireless and Mobile Systems. New York, USA: IEEE Computer Society, 2002: 61-68.

[14] KOROMA J, LI Wei. A generalized model for network survivability [C]// Proceedings of the 2003 Conference on Diversity in Computing (TAPIA 2003). Atlanta, Georgia, USA, 2003: 47-51.

[15] PENG San-cheng, JIA Wei-jia, WANG Guo-jun. Survivability evaluation in large-scale mobile ad-hoc networks [J]. Journal of Computer Science and Technology, China, 2009, 24(4): 761-774.

[16] HUANG X. Semi-Markov model of network traffic [D]. Graduate School of Chinese Academy of Sciences, China, 2006. (in Chinese)

[17] XING Fei, WANG Wen-ye. On the survivability of wireless ad hoc networks with node misbehaviors and failures [J]. IEEE Transactions on Dependable and Secure Computing, 2008, 7(3): 284-299.

[18] BOLLOBAS B. Modern graph theory [M]. New York: Springer, 1998: 216-240.

[19] PENROSE M D. On k-connectivity for a geometric random graph [J]. Random Structure Algorithms, 1999, 15(2): 145-164.

[20] FARAGO A. Scalable analysis and design of ad hoc networks via random graph theory [C]// Proceedings of the ACM Dial-M. Atlantic, Georgia, USA: ACM, 2002: 43-50.

[21] HU Y C, PERRIG A, JOHNSON D B. Ariadne: A secure on-demand routing protocol for ad hoc networks [J]. Wireless Networks, 2005, 11(2): 21-38.

[22] GONG Guang-lu, QIAN Min-ping. Tutorial on the application of random process & the stochastic model of algorithm and intelligent computing [M]. Beijing, China: Tsinghua University Press, 2004: 26-27. (in Chinese)

(Edited by YANG Bing)

Foundation item: Project(07JJ1010) supported by the Hunan Provincial Natural Science Foundation of China for Distinguished Young Scholars; Projects (61073037, 60773013) supported by the National Natural Science Foundation of China

Received date: 2010-06-12; Accepted date: 2010-10-27

Corresponding author: WANG Guo-jun, Professor, PhD; Tel: +86-731-88877711; E-mail: csgjwang@mail.csu.edu.cn, csgjwang@gmail.com