J. Cent. South Univ. Technol. (2011) 18: 672-678

DOI: 10.1007/s11771-011-0746-y

Modeling and parameter identification of amplitude- and frequency-dependent rubber isolator

SUN De-wei(孙德伟)¹, CHEN Zhi-gang(陈志刚)¹, ZHANG Guang-yu(张广玉)¹, P. Eberhard²

1. School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China;

2. Institute of Engineering and Computational Mechanics, University of Stuttgart, Stuttgart 70569, Germany

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Key words:

rubber isolator; modeling; parameter identification; hysteresis damping; dynamic analysis；

1 Introduction

Rubber isolators have many advantages such as compact structure, simple usage, high damping ratio, so they have been widely used in the field of vibration and noise control [1-2]. Despite rubber being so common, knowledge about the material properties is often poor. Because the dynamic stiffness of rubber isolators depends on not only the vibration frequency but also the vibration amplitude and environment temperature, insufficient knowledge of transmission and damping properties of rubber joints, as well as modeling techniques for rubber isolators, has often forced industry to carry out costly experimental work for optimizing the shape, location and volume of the units [3-4]. Nonetheless, some researchers proposed several models, such as the Kelvin-Voigt model, the Zener model, the Maxwell model and the viscoelastic fractional derivative model to analyze and predict the dynamic characteristics of rubber isolators [5-6]. Those models were extensively investigated by MEDALIA [7], PAYNE and WHITTAKER [8], SOMMER and MEYER [9]. In addition, experiment and system identification methods were often adopted to acquire parameters in different models and describe the dynamic characteristics [10-12].

Recently, the application of power functions, similar elliptical functions, or non-linear FEM to fit and identify the hysteresis loop also attracts much attention [13-14]. Some researches [15] used polynomial curve fitting to estimate the frequency-dependent rubber mount stiffness and damping characteristics by a complex frequency response function. The transition of the rubber mount stiffness from static to dynamic values was clarified. HOEFER and LION [16] provided a three-dimensional constitutive approach of finite nonlinear viscoelasticity to represent the rubber dynamic material behavior according to harmonic deformations under different frequencies and amplitudes.

On the other hand, a parameter identification method based on least square estimation in the frequency domain is developed for the Bouc-Wen model using experimental data from periodic vibration experiments. A bilinear hysteretic model is also an alternative method for hysteretic isolators [17]. The identification of nonlinear isolators using temporal and spectral methods was investigated. It was found that the non-integer exponent-type terms were the best for describing the nonlinear elastic force of the rubber [18]. The equivalent linearization technique was also developed to linearize governing nonlinear multi-degree-of-freedom equations of motion where responses of interest were calculated from the linear governing equations of motion [19].

Although the aforementioned researchers utilize many successful modeling, analysis and parameter identification methods for rubber isolator, it is still a challenge to determine an accurate and applicable method to predict its dynamic properties, especially under different loading conditions. This is why a single mathematical model is proposed, which can describe different types of springs, linear and nonlinear, and dampers, for example Coulomb damper, viscous damper, square damper, according to different coefficients and damping indices. It is also quite efficient to extract the spring force and the damping force from original measurement data with this model. This model is flexible and accurate for the simulation and prediction of the dynamic behaviors of rubber isolator over a broad frequency range.

In the mathematic model proposed in this work to describe the hysteresis characteristic of rubber isolators, amplitude- and frequency-dependent spring and damper coefficients are used. The spring and damper models whose coefficients change with amplitude and frequency are used to express the relationships between the nonlinear force and the displacement of rubber material. A damping index is employed to express different types of dampers. All these coefficients will be identified according to the vibration measurement data. Finally, comparisons with the experimental results are conducted to verify the usefulness of this method.

2 Model of hysteresis damping

The behavior of force f changing with the displacement x of a nonlinear isolation system is shown in Fig.1, displaying hysteresis damping. The damping hysteresis loop consists of two lines, the upper line and the lower line, which are anti-symmetric about the origin:

F_U(x)=-F_L(-x)                                    (1)

The forces, F_U and F_L, can be described by power functions [20] as

                         (2)

                    (3)

where F_U is the upper force and F_L is the lower force, a_i is the coefficient of the power functions, and q is the number of power functions depending on the shape of hysteresis curve and fitting precision. Then, combining Eqs.(2) and (3), we get

                                      (4)

where M should be set up as an odd number and sign(?) is the signum function. The nonlinear force F is next decomposed into a spring force F_s and a damping force F_d, as shown in Fig.1.

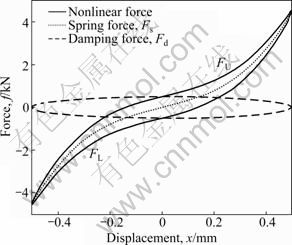
Fig.1 Hysteresis loop for rubber material

Furthermore, the spring force F_s and the damping force F_d can be expressed using the spring coefficient and damping coefficient in Eq.(5), which have relation with the vibration amplitude and frequency, as shown in Fig.2. These relations will be acquired by a parameter identification method:

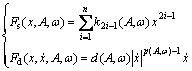                       (5)

where k_2i-1(A,ω) is the stiffness coefficient, d(A,ω) is a damping coefficient and p(A,ω) can indicate different types of dampers. All of them depend on the vibration amplitude A and the frequency ω.

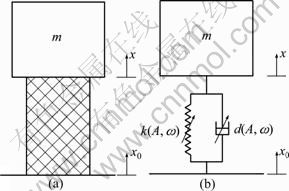
Fig.2 Sketch of amplitude- and frequency-dependent spring and damper: (a) Rubber isolator; (b) Model of amplitude- and frequency-dependent spring and damper

If p=0,  is the Coulomb damping force. If p=1,  means viscous damping. If p=2, F_d= means a square damping force. Moreover, the force F_s which is approximated by n-th order polynomials can express linear or nonlinear springs.

The consumed energy w_loss during a sine vibration cycle is calculated by

                (6)

where T=t₂-t₁, is one sine vibration period; x=Asin(ωt), is the displacement and Γ(?) represents the Gamma function.

According to Eq.(6), the consumed energy will be computed using this model, which can verify the correctness of the results of parameter identification by comparison with the originally measured data. This equation also indicates that the spring force does not consume energy during the sine vibration.

3 Identification of model spring and damper coefficients

In order to apply this idea to a real engineering problem, the dynamic characteristic of a rubber ring with thickness of 2 mm was investigated. Rubber hysteresis causes energy loss during vibration, which means that there is a phase separation between stress and strain, and there is a nonlinear relation between force and displacement of rubber material. So, to get the relation between force and displacement of rubber, a sinusoidal vibration test was conducted using an STI D-300-3 electromagnetic vibration test instrument. The maximal acceleration provided by this instrument can be up to  980 m/s² and the maximal displacement is 25 mm. The inside and outside of the rubber ring are fixed by a steel holding fixture, which is set on the vibration instrument. In the test, a displacement control mode was used, and a displacement sensor was set in the bottom of the holding fixture and a force sensor in the center of the holding fixture so as to acquire the response force of rubber rings under sine vibration load.

The rubber working frequency ranged from 5 to  100 Hz and the rubber deformation was from 0.2 to   0.5 mm. So, the frequencies of 5, 10, 20, 50 and 100 Hz were selected as frequency points of the vibration test and the displacements of 0.2, 0.3 and 0.5 mm were selected as amplitude points of the vibration test. The force and displacement signals from the sensors were filtered in order to eliminate high frequency noise. Fifteen data combinations for the rubber force changing with the displacement were measured for different frequencies and amplitudes. Some curves are shown in Figs.3 and 4.

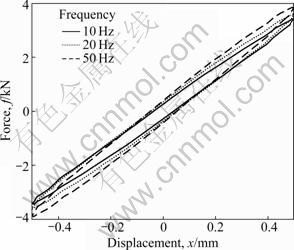
Fig.3 Measurement of forces changing with displacement for amplitude of 0.5 mm

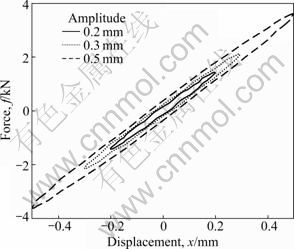
Fig.4 Measurement of forces changing with displacements for frequency of 20 Hz

After acquiring the measured test data, the parameter identification method was applied to identify the coefficients of spring and damper. The program flow implemented in Matlab is shown in Fig.5.

First step of the order n=1 is assumed in Eq.(5) according to the shapes of measurement curves in Figs.3 and 4. This means that the measurement force is simulated by a linear spring force and a nonlinear damping force. Then, the calculation force is obtained:

      (7)

The parameter identification method determining k, d and p in a certain sine vibration process, whose vibration frequency and amplitude are known, is based on the nonlinear least square method using the Matlab. The Levenberg-Marquardt method is used as the solution algorithm. The objective function is

          (8)

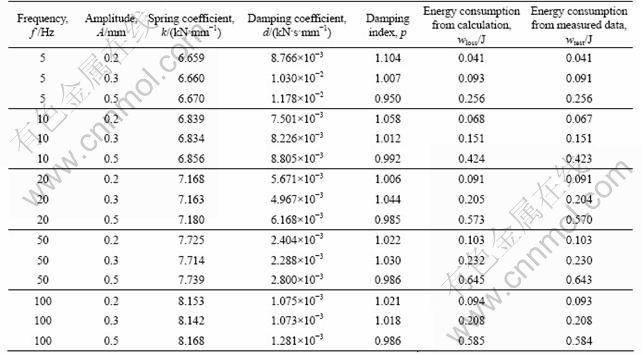
where F_cal(x_i) is the calculation force from Eq.(7) and F_mea(x_i) is the measurement force from the vibration experiment. N is the number of measurement data. Repeating this identification process, different k, s and p will be obtained in different vibration frequencies and amplitudes. The identification results are listed in Table 1 corresponding to frequencies and amplitudes.

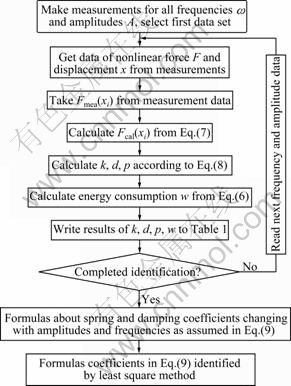
Fig.5 Flow chart for identification of spring and damper coefficients

The resulting spring coefficients, damping coefficients and damping index mainly change with the vibration frequency and amplitude. So, three equations are assumed in order to describe the relations of k, d and p changing with ω and A in Eq.(9). According to the data in Table 1, similarly applying the nonlinear least square method to fit the coefficients in Eq.(9), the spring coefficients, damping coefficients and damping index changing with frequencies and amplitudes would be computed:

                      (9)

where k₁=6.791 4, k₂=2.214 8×10^-3, k₃=3.178 2×10^-4, d₁=1.000 9×10^-2, d₂=6.977 6×10^-1, d₃=-7.098 3×10^-3, d₄=5.347 6×10^-6, p₁=1.091 5, p₂=-2.061 9×10^-1, p₃= -1.978 1×10^-5.

According to Eq.(9), the curves are reconstructed for verification, as shown in Fig.6. This identification method can be applied not only to rubber materials, but also to other materials having hysteresis damping, which can be approximated by the above method.

Table 1 Identification results of spring and damper coefficients from measured data

4 Modeling and dynamic analysis of rubber isolator

In order to apply this method to a real engineering example, a structure including rubber rings was investigated and its dynamic characteristics were analyzed. As shown in Fig.7, the sinusoidal vibration experiment was conducted for a hollow shaft system supported by two rubber rings using an STI D-300-3 electromagnetic vibration test instrument. The acceleration load as shown in Fig.8 was exerted in the bottom of the system and an acceleration sensor was placed in the middle of the hollow shaft to receive the acceleration response. On the other hand, for the simulation, the spring coefficient k(A,ω), damper coefficient d(A,ω) and damper index p(A,ω) in Eq.(9) were applied to establish the dynamics of the hollow shaft system. The rubber ring forces were simulated by Eqs.(7) and (9) and the hollow shaft was regarded as a block with mass m, as shown in Fig.9.

The vibration frequencies are from 10 to 100 Hz and 20 Hz is the corner frequency, as shown in Fig.8. The maximal acceleration can be up to 10.5g, where g denotes the gravity acceleration. In the dynamic equations, the acceleration is also regarded as the input variable solving the corresponding response in the center of mass of the shaft. Comparisons of the response accelerations of experiment and calculation demonstrate the usefulness of this method.

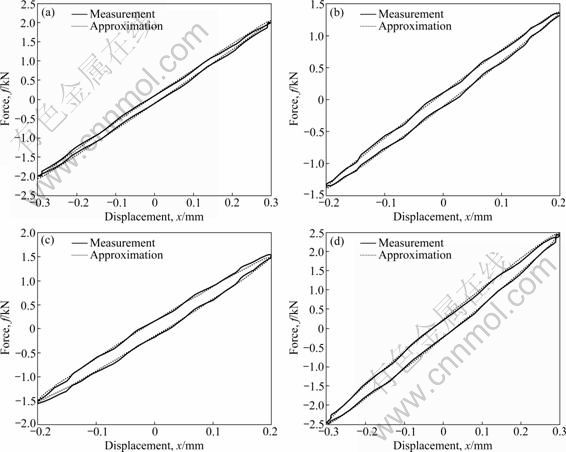
Fig.6 Comparisons of approximation and measured data: (a) f=5 Hz, A=0.3 mm; (b) f=10 Hz, A=0.2 mm; (c) f=50 Hz, A=0.2 mm;   (d) f=100 Hz, A=0.3 mm

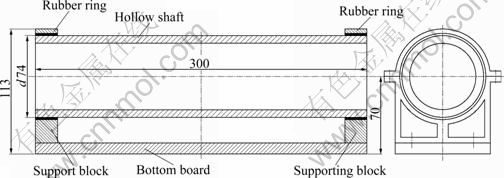
Fig.7 Hollow shaft model supported by rubber rings (Unit: mm)

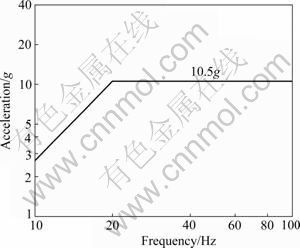
Fig.8 Input acceleration at bottom of model

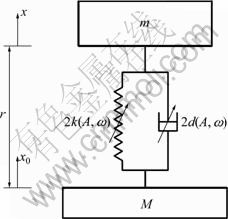
Fig.9 Dynamic model of rubber rings supporting system

The system differential equations are

       (10)

where m is the mass of the hollow shaft, m=4.565 kg, x means the response displacement of hollow shaft, x₀ is the displacement of bottom board, r is the relative displacement, r=x-x₀, 2k(A, ω)/m, ε=2d(A, ω)/m.

The differential equation is solved using complex numbers to express r and x₀. Set x₀=a₀exp(jωt), r=A_rexp(jωt); A_r=a_rexp(-jα). Then, put them into Eq.(10), and we get

                                 (11)

By algebraic simplification, we get

           (12)

where ω₀ and ε can be calculated from k(A,ω) and d(A,ω), j is the imaginary number, a₀ is the vibration amplitude of bottom board, ω is the circular frequency. And a_r and α can be computed by Eq.(12) according to the rule of complex number using the method of numerical analysis. Further r can be got. Because x=x₀+r, the response acceleration of hollow shaft  can also be acquired.

According to the vibration experiment, the maximal response of acceleration is up to 10.85g (100 Hz). Compared with the result from Eq.(12), the maximal acceleration can reach 11.77g (100 Hz), and the maximal inaccuracy is 8.5%, which contains the parameter identification errors, sensor errors and model simplification errors, etc. The results are compared in Fig.10.

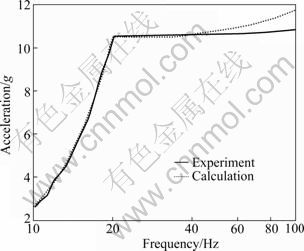
Fig.10 Comparison of acceleration response between experiment and calculation

5 Conclusions

For modeling and analysis of rubber isolators, a method using amplitude- and frequency-dependent coefficients in a spring and damper approximation is proposed to describe the hysteresis damping. Namely, the rubber isolator is represented by a parallel spring damper model, whose coefficients can be identified from measurements. Further, the coefficients changing with amplitudes and frequencies are fitted by a nonlinear least square method from measurement data. Finally, this method is used to model a hollow shaft system. Compared with the result of vibration experiments, the maximal inaccuracy is 8.5%, which can often satisfy the engineering requirements. This method can simplify the modeling and dynamic analysis of rubber components.

References

[1] FAN Z J, LEE J H, KANG K H, KIM K J. The forced vibration of a beam with viscoelastic boundary supports [J]. Journal of Sound and Vibration, 1998, 210(5): 673-676.

[2] TARRAGO M J, KARI L, VINOLAS J, GIL-NEGRETE N. Frequency and amplitude dependence of the axial and radial stiffness of carbon-black filled rubber bushings [J]. Polymer Testing, 2007, 26: 629-638.

[3] GIL-NEGRETE N, VINOLAS J, KARI L. A simplified methodology to predict the dynamic stiffness of carbon-black filled rubber isolators using a finite element code [J]. Journal of Sound and Vibration, 2006, 296: 757-776.

[4] ZHANG J, RICHARDS C M. Parameter identification of analytical and experimental rubber isolators by Maxwell models [J]. Mechanical Systems and Signal Processing, 2007, 21: 2814-2816.

[5] KWOK N M, HA O P, NGUYEN M T, SAMALI B. Bous-Wen model parameter identification for a MR fluid damper using computationally efficient GA [J]. ISA Transactions, 2007, 46: 167-178.

[6] PAN Xiao-yong, CHAI Guo-zhong, SHANGGUAN Wen-bin. Experiment and calculation on the time response of a system including rubber isolator [J]. Journal of Vibration and Shock, 2007, 26: 32-33. (in Chinese)

[7] MEDALIA A I. Effects of carbon black on dynamic properties of rubber [J]. Rubber Chemistry and Technology, 1978, 51: 437-523.

[8] PAYNE A R, WHITTAKER R E. Low strain dynamic properties of filled rubbers [J]. Rubber Chemistry and Technology, 1971, 44: 440-478.

[9] SOMMER J G, MEYER D A. Factors controlling the dynamic properties of elastomeric products [J]. Journals of Elastomers and Plastics, 1974, 6: 49-68.

[10] JURADO F J, MATEO A, GIL-NEGRETE N, VINOLAS J, KARI L. Testing and FE modelling of the dynamic properties of carbon black filled rubber [C]// Proceedings of the EAEC, Conference I. Barcelona, 1999: 119-126.

[11] DEAN G D, DUNCAN J C, JOHNSON A F. Determination of nonlinear dynamic properties of carbon-black filled rubbers [J]. Polymer Testing, 1984, 4: 225-249.

[12] WANG M J. Effect of polymer-filler and filler-filler interactions on dynamic properties of filled vulcanizates [J]. Rubber Chemistry and Technology, 1998, 71: 520-589.

[13] WU J, SHANGGUAN W. Modeling and applications of dynamic characteristics for rubber isolators using viscoelastic fractional derivative model [J]. Engineering Mechanics, 2008, 50: 162-165. (in Chinese)

[14] MORDINI A, STRAUSS A. An innovative earthquake isolation system using fiber reinforced rubber bearings [J]. Engineering Structures, 2008, 30: 2739-2741.

[15] LIN T, FARAG N H, PAN J. Evaluation of frequency dependent rubber mount stiffness and damping by impact test [J]. Applied Acoustics, 2005, 66: 829-844.

[16] HOEFER P, LION A. Modelling of frequency- and amplitude-dependent material properties of filler-reinforced rubber [J]. Journal of the Mechanics and Physics of Solids, 2009, 57: 500-520.

[17] TAN R Y, HUANG M C. System identification of a bridge with lead-rubber bearings [J]. Computer and Structures, 2000, 74: 267-280.

[18] RICHARDS C M, SINGH R. Identification of nonlinear properties of rubber isolators using experimental and analytical methods [C]// Proceeding on Noise Control Engineering. Michigan, USA, 1998: 391-396.

[19] HONG W K, KIM H C. Performance of a multi-story structure with a resilient-friction base isolation system [J]. Computer and Structures, 2004, 82: 2271-2283.

[20] GONG Xian-sheng, XIE Zhi-jiang, LUO Zhen-huang, ZHANG Mei. The characteristics of a nonlinear damper for vibration isolation [J]. Journal of Vibration Engineering, 2001, 14: 334 Z.338. (in Chinese)

(Edited by YANG Bing)

Foundation item: Project(50675042) supported by the National Natural Science Foundation of China

Received date: 2010-03-08; Accepted date: 2010-06-25

Corresponding author: SUN De-wei, PhD; Tel: +86-451-86413111; E-mail: sdw1981@yahoo.com.cn