J. Cent. South Univ. Technol. (2011) 18: 1441-1447

DOI: 10.1007/s11771-011-0859-3

Optimization of processing parameters for microwave drying of selenium-rich slag using incremental improved back-propagation neural network and response surface methodology

LI Ying-wei(李英伟)^{1, 2}, PENG Jin-hui(彭金辉)^{1, 2}, LIANG Gui-an(梁贵安)²,

LI Wei(李玮)², ZHANG Shi-min(张世敏)²

1. Faculty of Metallurgical and Energy Engineering, Kunming University of Science and Technology,Kunming 650093, China;

2. Key Laboratory of Unconventional Metallurgy, Ministry of Education,

Kunming University of Science and Technology, Kunming 650093, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Key words:

microwave drying; response surface methodology; optimization; incremental improved back-propagation neural network; prediction；

1 Introduction

Microwave technology, with the characteristics of instantaneity, integrity, efficiency, safety, non-pollution and selective heating to the polar water molecules, is widely applied in the drying. The microwave magnetron can generate electromagnetic energy which can be transformed to internal energy in the interior of the dielectric materials [1-4].

In the microwave drying process, the influencing factors of microwave drying including the microwave input power, the acting time, the initial moisture content, the average material mass, the average material surface area and the rotational frequency have different affecting degrees in the drying process, which causes the longer testing cycle and the larger testing quantity. The parameters are difficult to be optimized.

In the present study, the experimental conditions are optimized by using central composite design (CCD) in response surface methodology (RSM), which is an empirical statistical modeling technique employed for multiple regression analysis using quantitative data obtained from properly designed experiments to solve multivariate equations simultaneously, obtaining the optimal process conditions through building up RSM optimization model [5-12].

And the back-propagation (BP) neural network, which has the ability of non-linear mapping, is chosen to build up the simulation model to predict the experimental process. The traditional BP neural network needs long convergent time and sometimes the convergent results cannot be obtained because of local minimum areas. The improved BP neural network based on the Levenberg-Marquardt (L-M) algorithm overcomes these limitations [13-17]. In the process of training the network, there are many problems. Much training data are probably offered by the way of increment batch and the limitation of the system memory can make the training data infeasible when the sample scale is large. Then, the incremental improved BP neural network is put forward [18-23].

2 Incremental improved back-propagation neural network

The BP neural network, as shown in Fig.1, has a massively interconnected network structure consisting of many simple processing neurons capable of performing parallel computation for data processing. It is made of an input layer, an output layer and a number of hidden layers in which neurons are connected to each other with modifiable weighted interconnections.

In Fig.1, x_i is the input; y_h is the output of one node in the hidden layers; z_j is the output of one node in the output layer; T_j is the target output; ω_ih is the weight between the i-th node in the input layer and the h-th node in the hidden layers; ω_hj is the weight between the h-th node in the hidden layers and the j-th node in the output layer; N₁ is the number of node in the input layer; N₂ is the number of node in the hidden layers; N₃ is the number of node in the output layer.

The performed functions are expressed as the following equations:

The function of one node in hidden layers:

                                               (1)

The function of one node in output layer:

                    (2)

The error function:

                                                      (3)

The sigmoid transfer function:

                                                              (4)

where θ_h is the threshold value of the h-th node; γ_j is the threshold value of the j-th node.

The L-M algorithm [13-17] is designed to approach the second-order training speed without having to compute the Hessian matrix. The L-M algorithm applies this approximation to the Hessian matrix in the following Newton-like update:

                                (5)

where J is the Jacobian matrix that contains the first derivatives of the network errors with respect to the weights and biases, and E is a vector of network errors. The Jacobian matrix can be computed through a standard back-propagation technique that is much less complex than that by computing the Hessian matrix. μ is a scalar. When μ is zero, it is just Newton’s method, using the approximate Hessian matrix. When μ is large, it becomes gradient descent with a small step size.

The incremental learning is implemented by adjusting the weights of the BP neural network [18-23]. The effective extent of knowledge is settled based on the prior knowledge; the weight vector can be changed in the effective extent when the accuracy of the learned knowledge is unchanged. The weight is adjusted through the fixed network structure when the new sample is provided. This can make the indication value approach to the target value, and then the new sample knowledge is learned. So, the network can not only learn the new sample knowledge but also hold the original knowledge.

With the incremental learning, a scaling factor, s, which scales down all weight adjustments, is introduced, so all the weights are within bounds. The learning rule is

                                   (6)

where Δω_ab is the weight between the a-th node and the b-th node of all the network layers; η (0<η<1) is a trial-independent learning rate; δ_b is the error gradient at the b-th node; O_a is the activation level at the a-th node; the parameter k is the k-th iteration.

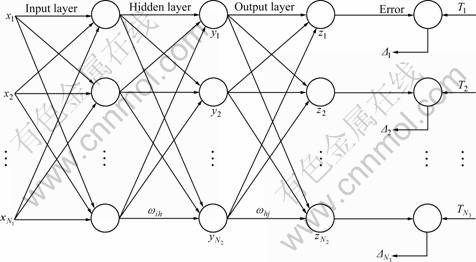
Fig.1 BP neural network configuration

3 Response surface methodology

The response surface methodology (RSM) is a collection of mathematical and statistical techniques that are useful for the modeling and analysis of problems in which a response of interest is influenced by several quantifiable variables or factors, with the objective of optimizing the response. Central composite design (CCD) method is suitable for fitting a quadratic surface and it helps to optimize the effective parameters with a minimum number of experiments, as well as to analyze the interaction between the parameters [5].

A full second-order polynomial model is fitted to the experimental data and the coefficients of the model equation are determined. The result in an empirical model related to the response is

        (7)

where y is the predicted response, n is the number of

factors, α₀ is the constant coefficient, α_i is the linear coefficient, α_ii is the quadratic coefficient, and α_ij is the interaction coefficient.

4 RSM optimization model

4.1 Data preprocessing

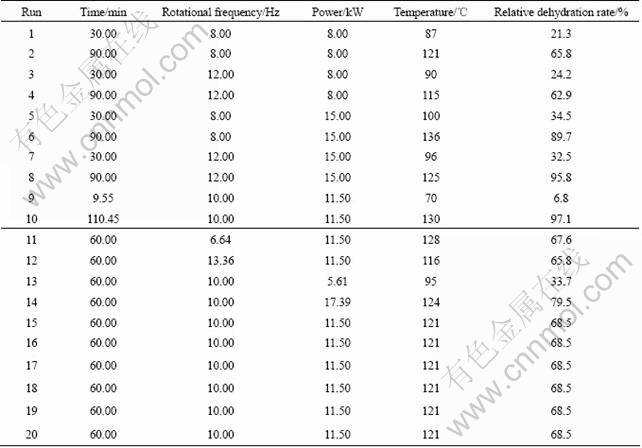
In the experiment, the water content of selenium- rich slag was 38% (mass fraction) after pretreatment, the average mass of selenium-rich slag for each layer was  12 kg and the average material surface area was 0.15 m². Three input variables were used: the acting time x₁, the rotational frequency x₂ and the microwave power x₃; two output variables were used: the relative dehydration rate d and the material temperature t.

4.2 RSM optimization model

By analyzing the data in Table 1, the multiple quadratic regression equations of the temperature, the relative dehydration rate on the time, the rotational frequency and the microwave power is obtained:

                                                             (8)

                                                            (9)

Table 1 Experimental results designed by RSM

The variance analyses of the temperature and the relative dehydration rate quadratic model are listed in Table 2 and Table 3, respectively.

According to Table 2 and Table 3, the conclusions are drawn as follows. The respective Model F-Values of 101.63 and 89.80 imply that the models are significant. There is only a 0.01% chance that a “Model F-Value” could occur due to noise. Values of “Probability>F” are less than 0.05, indicating that model terms are significant. The respective values of “R-squared” are 0.989 2 and 0.987 8, indicating that the models are considered relatively higher as the value is close to unity, showing that there is a good agreement between the experimental and the predicted temperature results and relative dehydration rate results from respective model.

Figure 2 shows the three-dimensional response surface diagrams. When the irradiation time and the rotational frequency are held constant, the temperature and the relative dehydration rate increase with the increase of microwave power. Under constant irradiation time and microwave power, the temperature and the relative dehydration rate change only a little with the increase of rotational frequency. Under constant microwave power and the rotational frequency, the temperature and the relative dehydration rate increase with the increase of irradiation time. The microwave power and the irradiation time have the significant effect on the temperature and the relative dehydration rate, and the rotational frequency has no obvious effect on the temperature and the relative dehydration rate.

The optimal experimental conditions are listed in Table 4. In the optimum operating conditions, the incremental improved BP neural network prediction model can predict the drying process results and the different effects on the results of the independent variables, as listed in Table 5. After three verification experiments, the average acting time is 90 min, the average rotational frequency is 10.5 Hz, the average microwave power is 14.8 kW, the average temperature is 131 °C and the average relative dehydration rate is 96.51%. These demonstrate that the optimal experimental conditions of the RSM and the prediction results of the incremental improved BP neural network are feasible.

Table 2 Variance analysis of temperature quadratic model

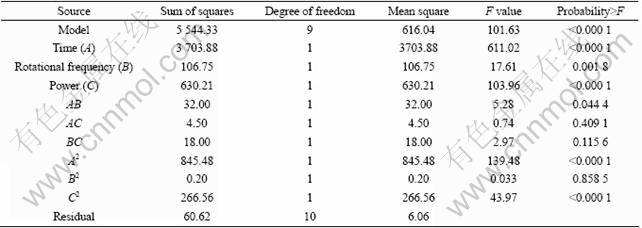
Table 3 Variance analysis of relative dehydration rate quadratic model

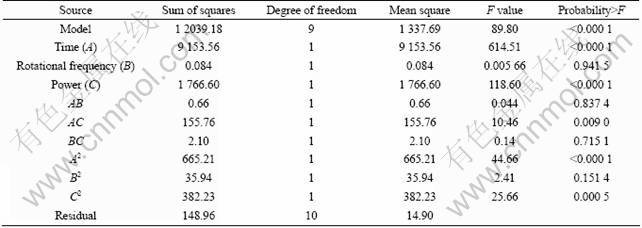
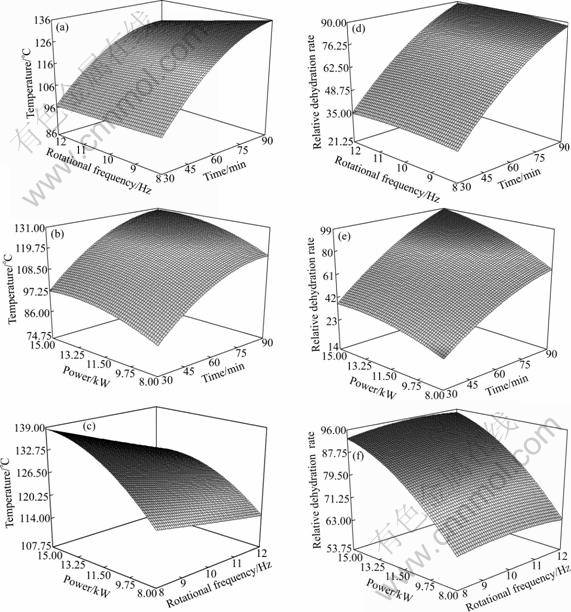
Fig.2 Three-dimensional response surface diagrams: (a) and (d) Microwave power of 12.00 kW; (b) and (e) Rotational frequency of 11.00 Hz; (c) and (f) Irradiation time of 85 min

Table 4 Optimal conditions and results using RSM

Table 5 Predicted results using incremental improved BP neural network

5 Incremental improved BP neural network prediction model

In order to train the network conveniently and reflect the interrelations of the various factors preferably, the sample data must be pre-treated. In the training process, the number of layers of the hidden layer is determined and the network weights and threshold values are obtained through computing the minimum value of the error function. The optimum number of units of the hidden layers is 5 after training the network. When the network training is finished, the training network is tested, the non-training sample data are read to predict the results, and the output data are calculated and compared with the measured data. If the error is within the regulated scope, the neural network model is available and the simulation can be carried on.

The optimal experimental conditions and results designed by RSM are predicted by the incremental improved BP neural network, and the set target convergence accuracy is reached by comparing and analyzing the output and measured data of training and prediction and 166 times of iteration of the network.

Figure 3 shows the predicted impacts of the acting time, the rotational frequency and the microwave power on the temperature and the relative dehydration rate.

When the irradiation time and the rotational frequency are held constant, the temperature and the relative dehydration rate increase with the increase of microwave power. Under constant irradiation time and microwave power, the temperature and the relative dehydration rate change only a little with the increase of rotational frequency. And under constant microwave power and rotational frequency, the temperature and the relative dehydration rate increase with the increase of irradiation time. The microwave power and the irradiation time have the significant effect on the temperature and the the relative dehydration rate, and the rotational frequency has no obvious effect on the temperature and the relative dehydration rate. The predicted values of the incremental improved BP neural network fit well to the actual values, and the mean square error is 0.16. The results of the irradiation time, the rotational frequency and the microwave power impact on the temperature and the relative dehydration rate are the same as the analysis results obtained from RSM. According to the verification experiments, the incremental improved BP neural network industrial prediction model can predict the drying process results and the different effects on the results of the independent variables can verify the accuracy of the optimum operating results obtained from the quadratic form of the RSM. The combination of the RSM industrial optimization model and the incremental improved BP neural network industrial prediction model can provide the basis for the production practice.

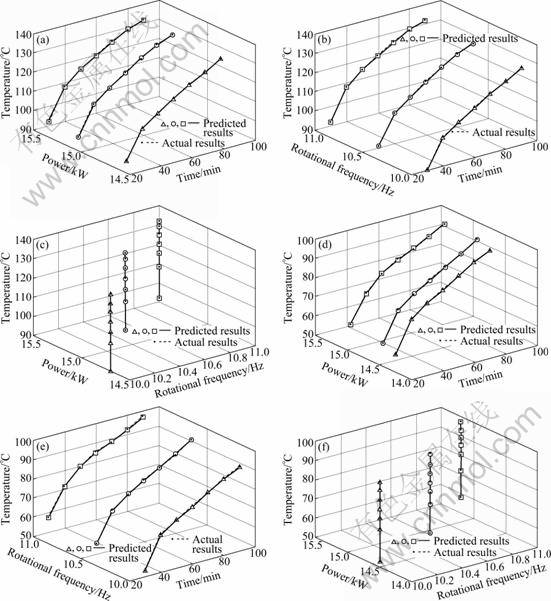
Fig.3 Three-dimensional diagrams using incremental improved BP neural network: (a) Effect of time and power on temperature;   (b) Effect of time and rotation frequency on temperature; (c) Effect of rotational frequency and power on temperature; (d) Effect of time and power on relative dehydration rate; (e) Effect of time and rotational frequency on temperature; (f) Effect of rotational frequency and power on temperature (△—Time: 10-90 min, Frequency: 10 Hz, Power: 14.5 kW; ○—Time: 10-90 min; Frequency: 10.5 Hz, Power: 14.7 kW; □—Time: 10-90 min, Frequency: 11 Hz, Power: 15.2 kW)

6 Conclusions

1) The optimum operating conditions using RSM optimization model are: the microwave power of   14.97 kW, the acting time of 89.58 min, the rotational frequency of 10.94 Hz, the temperature of 136.407 °C, and the relative dehydration rate of 97.1895%. With the optimization model, the temperature and the relative dehydration rate of correlation coefficient are 0.989 2 and 0.987 8, which indicate that RSM can optimize the experimental conditions within much more broad range by considering the combination of factors.

2) The predicted results with the optimum operating conditions using the incremental improved BP neural network are: the microwave power of 14.5-15.2 kW, the acting time of 90 min, the rotational frequency of 10.0- 11.0 Hz, the temperature of 130-132 °C, and the relative dehydration rate of 95.89%-96.95%, and the mean square error of the prediction model is 0.16, which indicate that the model can predict the results effectively and provide the theoretical guidance for the follow-up production process.

References

[1] FITO P, CHIRALT A. Food matrix engineering: The use of water-structure-functionality ensemble in dried food product development [J]. Food Science and Technology International, 2003, 9(3): 151-156.

[2] AGUILERA J M, CHIRALT A, FITO P. Food dehydration and product structure [J]. Trends in Food Science & Technology, 2003, 14(10): 432-437.

[3] PENG Jin-hui, YANG Xian-wan. The new applications of microwave power [M]. Yunnan: Yunnan Science & Technology Press, 1997. (in Chinese)

[4] FITO P, CHIRALT A, BARAT J M. Vacuum Impregnation for development of new dehydrated products [J]. Journal of Food Engineering, 2001, 49(4): 297-302.

[5] JAGANNADHA RAO K, KIM C H, RHEE S K. Statistical optimization of medium for the production of recombinant hirudin from Saccharomyces cerevisiae using response surface methodology [J]. Process Biochemistry, 2000, 35(7): 639-647.

[6] AKTAS N. Optimization of biopolymerization rate by response surface methodology (RSM) [J]. Enzyme and Microbial Technology, 2005, 37(4): 441-447.

[7] PENG Zhen-bin, LI Jun, PENG Wen-xiang. Application analysis of slope reliability based on Bishop analytical method [J]. Journal of Central South University: Science and Technology, 2010, 41(2): 668-672. (in Chinese)

[8] ZHONG Ming, HUANG Ke-long, ZENG Jian-guo, LI Shuang, ZHANG Li. Determination of contents of eight alkaloids in fruits of Macleaya cordata (Willd) R. Br. From different habitats and antioxidant activities of extracts [J]. Journal of Central South University of Technology, 2010, 17(3): 472-479.

[9] ZAINUDIN N F, LEE K T, KAMARUDDIN A H, BHATIA S, MOHAMED A R. Study of absorbent prepared from oil palm ash (OPA) for flue gas desulfurization [J]. Separation and Purification Technology, 2005, 45(1): 50-60.

[10] AZARGOHAR R, DALAI A K. Production of activated carbon from Luscar char, Experimental and modelling studies [J]. Microporous and Mesoporous Materials, 2005, 85(3): 219-225.

[11] KALIL S J, MAUGERI F, RODRIGUES M I. Response surface analysis and simulation as a tool for bioprocess design and optimization [J]. Process Biochemistry, 2000, 35(6): 539-550.

[12] ROUX W J, STANDER N, HAFTKA R T. Response surface approximations for structural optimization [J]. International Journal for Numerical Methods in Engineering, 1998, 42(3): 517-534.

[13] KERMANI B G, SCHIFFMAN S S, NAGLE H T. Performance of the Levenberg-Marquardt neural network training method in electronic nose applications [J]. Sensors and Actuators B-Chemical, 2005, 110(1): 13-22.

[14] SINGH V, INDRA G, GUPTA H O. ANN-based estimator for distillation using Levenberg-Marquardt approach [J]. Engineering Applications of Artificial Intelligence, 2007, 20(2): 249-259.

[15] LERA G, PINZOLAS M. Neighborhood based Levenberg-Marquardt algorithm for neural network training [J]. IEEE Transactions on Neural Networks, 2002, 13(5): 1200-1203.

[16] ADELOYE A J, MUNARI A D. Artificial neural network based generalized storage-yield-reliability models using the Levenberg- Marquardt algorithm [J]. Journal of Hydrology, 2006, 362(1/2/3/4): 215-230.

[17] MIRZAEE H. Long-term prediction of chaotic time series with multi-step prediction horizons by a neural network with Levenberg-Marquardt learning algorithm [J]. Chaos, Solitons & Fractals, 2009, 41(4): 1975-1979.

[18] LI Ying-wei, YU Zheng-tao, MENG Xiang-yan, CHE Wen-gang, MAO Cun-li. Question classification based on incremental modified Bayes [C]// Proceedings of the 2008 2nd International Conference on Future Generation Communication and Networking, FGCN 2008: 149-152.

[19] FU Li-min, HSU Hui-huang, PRINCIPE J C. Incremental back-propagation learning network [J]. IEEE Transactions on Neural Networks, 1996, 7(3): 757-761.

[20] KARAYIANNIS N B, MI G W Q. Growing radial basis neural networks: Merging supervised and unsupervised learning with network growth techniques [J]. IEEE Transactions on Neural Networks, 1997, 8(6): 1492-1506.

[21] GHOSH J, NAG A C. Knowledge enhancement and reuse with radial basis function networks [C]// Proceeding of the International Joint Conference on Neural Networks, 2002: 1322-1327.

[22] PAREKH R, YANG J H, HONAVAR V. Constructive neural network learning algorithms for pattern classification [J]. IEEE Transactions on Neural Networks, 2000, 11(2): 436-451.

[23] ZHANG J, MORRIS A J. A sequential learning approach for single hidden layer neural networks [J]. Neural Networks, 1998, 11(1): 65-80.

(Edited by YANG Bing)

Foundation item: Project(50734007) supported by the National Natural Science Foundation of China

Received date: 2010-09-25; Accepted date: 2011-01-14

Corresponding author: PENG Jin-hui, Professor, PhD; Tel: +86-871-5191046; E-mail: jhpeng@kmust.edu.cn