八足仿蟹机器人行走稳定性分析

王立权¹，王海龙¹，陈曦²，许俊伟¹，任梦轩¹

(1. 哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨，150001；

2. 哈尔滨工程大学 自动化学院，黑龙江 哈尔滨，150001)

摘 要：

圆弧形足端结构的八足机器人行走稳定性及稳定裕量，提出1种适用于八足机器人行走稳定性判定方法。对八足机器人整体结构进行抽象简化；使用闭环矢量法获得了质心与落足点之间的相对位置关系；应用规范化能量稳定裕度(S_NESM)方法对八足机器人静态稳定性进行描述，建立复杂环境下机器人静态稳定裕度的数学模型。通过数值仿真获得了机器人稳定裕度与机体质心高度及地面倾角之间的关系。稳定性实验结果表明：该方法能够准确判定八足机器人的行走稳定性。

关键词：

八足机器人；规范化能量稳定裕量(NESM)；稳定裕度；

中图分类号：TP242          文献标志码：A         文章编号：1672-7207(2014)10-3416-07

Walking stability analysis of an octopod crab-like robot

WANG Liquan¹, WANG Hailong¹, CHEN Xi², XU Junwei¹, REN Mengxuan¹

(1. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China;

2. College of Automation, Harbin Engineering University, Harbin 150001, China)

Abstract: A stability judging method for octopod robot was proposed, in order to exactly evaluate the walking stability and stability margin of a new octopod robot with circular-arc knuckle structure. The structure of the octopod robot was simplified. The relative position between the centroid and touchdown point was calculated by closed-loop vector method. According to the static stability of the octopod robot which was demonstrated by the method of normalized energy stability margin (NESM), a static stability margin mathematical model of a robot in complex conditions was given. According to the results of numerical simulation, the relationship between stability margin and the center of mass height, ground angle was proposed. Experiment based on the proposed method is carried out and the results verify that the proposed method can accurately judge the octopod robot walking stability.

Key words: octopod; normalized energy stability margin (NESM); stability margin

足式机器人相对于轮式或履带式机器人的主要优势就是在崎岖不平的路面上实现稳定行走 ^[1-3]。足式机器人运动过程中要满足行走稳定性要求，即不能发生倾翻。在运动过程中，若发生倾翻，则可能导致机器人结构件损坏、系统失控、作业失败乃至整个系统报废等一系列问题^[4]，因此，倾翻稳定性研究对于足式机器人而言是至关重要的。现有的文献中，提出了几种关于多足机器人稳定性的判定方法。其中McGhee和Frank在20世纪60年代提出的重心投影法(CG projection method)是最早的静态稳定性判别方法，其定义为机器人质心在落地足支撑面的垂直投影点到支撑多边形的最短距离。该方法的不足之处是只能处理平坦地面的稳定性，而无法处理非平坦路面^[5]。为了更好地描述稳定性，Messuri于1985年提出了能量稳定裕度(energy stability margin, ESM)的方法，即将机器人当前势能与倾倒过程中最大的势能差作为稳定裕量衡量准则，该方法无论对于平坦路面还是非平坦的路面都是最适合的^[6]。按照ESM的理论，机器人的稳定性与其质量成正比，但事实并非如此，随着机器人质量的增加，外界的干扰因素也随之增大，机器人的稳定性并不会成比例增长。鉴于此，Messuri和Klein对能量稳定裕量进行改进，考虑到质量对稳定性的影响，提出规范化能量稳定裕度^[1] (normalized energy stability margin, NESM)。2005年Garcia等^[7]对规范化能量稳定裕量进行了修改，将惯性力影响考虑到推导过程中，提出了规范化动态能量稳定裕度(normalized dynamic energy stability margin, NDESM)，使其可以作为动态稳定性判定准则。但是，该方法没有考虑外界的干扰力矩项。王鹏飞等^[8]提出了采用支撑面压力中心至各落足点所形成的支撑凸多边形各边的最短距离来评定机器人行走稳定性。李斌等^[4]提出了稳定锥(stability pyramid technique, SPT)方法，用倾翻稳定性指数对可重构机器人的稳定性进行综合判定。田海波等^[9]针对轮腿式变形机器人，采用倾翻稳定性指数和能量稳定锥方法对机器人的运动稳定性进行综合评价，提出了动态能量稳定锥的方法(dynamic energy stability pyramid method, DESPM)，但没有对感知系统设置、运算速度等进行考虑，因此，还不能用于解决实际问题。总体说来，现有的几种稳定性评价方法并不完善，仍有待进一步研究。为准确评价具有圆弧形指节结构八足机器人的运动稳定性，本文将上述稳定性判定方法的不足之处进行全面考虑，对NESM进行改进，并将其应用于八足机器人运动稳定性研究中。

1  八足机器人

八足仿蟹机器人的三维模型如图1所示。机器人总体结构包括了步行足和躯干2部分。矩形的躯干底板是机器人各系统的载体，底板与步行足之间通过弹性梁连接。仿蟹机器人以横向行走为主要的行走方式，为简化结构提高效率，八条步行足在机体上平行对称布置。每条步行足由基节、股节、胫节和指节4部分组成，各关节采用串联开式链方式连接，胫节和指节之间无相对运动，除指节外其余三关节的设计采用模块化设计思想，新型的模块化驱动关节由微型直流伺服电机通过蜗轮蜗杆减速器输出扭矩，蜗轮蜗杆减速器的自锁特性使机器人即使在掉电的情况下依然能够保持掉电前的姿态，该模块化关节具有传动间隙小、输出扭矩大、互换性好、容易维修等优点^[10-12]。圆弧形指节结构使机器人在运动过程能够产生类滚动的运动效果，使运动更加的平稳。新型仿蟹机器人的技术参数如表1所示。机器人的足端配备了力传感器用于检测步行足与地面的接触力，在机器人的机体上方安放了电子罗盘、GPS和陀螺仪等传感器用于机器人的导航定位和内部工作状态的检测。

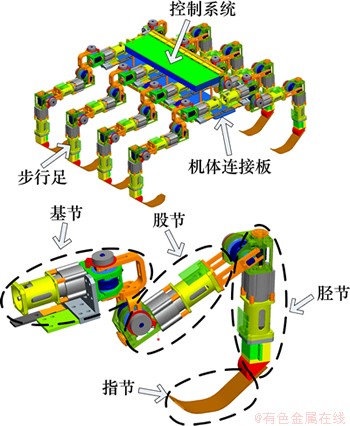
图1  八足仿蟹机器人3维模型

Fig.1  3D model of a octopod crab-like robot

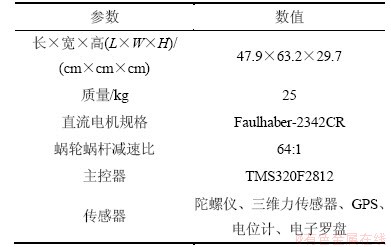
表1  八足仿蟹机器人技术参数

Table 1  Technical parameter of a octopod crab-like robot

2  数学模型

多足机器人机体质心距站立面的高度和质心与落足点的相对位置关系对机器人行走稳定性有着至关重要的影响，首先对八足仿蟹机器人结构方案进行抽象和简化，然后对简化后的机器人机构进行运动学分析，获得质心高度、跨距与机器人各关节角度之间的关系，以便对机器人八足行走稳定性进行研究。

当八足仿蟹机器人处于行走或者站立状态下，机器人躯体、步行足和支撑地面构成一个具有不同支链数并联机构^[13]。由于八足机器人布局采用平行对称的方式，机器人横行时可将其空间并联机构简化为平面5连杆机构，简化后机器人机构简图如图2所示。其中θ₁和θ₃为单步行足股节与机体轴线之间的夹角，θ₂和 θ₄为胫节与相邻股节的夹角，机器人股节、胫节和躯体的长度分别用L₁，L₂和L₃表示。为了使电子罗盘能够采集正确的地磁偏角，保障机器人定位导航系统的正常工作，八足机器人在实际行走过程中其机体应始终处于水平状态。机器人特殊的圆弧形指节结构，假设在行走过程中没有滑动只有纯滚动运动，机器人机体高度h和前后落足点之间的跨距s应始终保持不变。

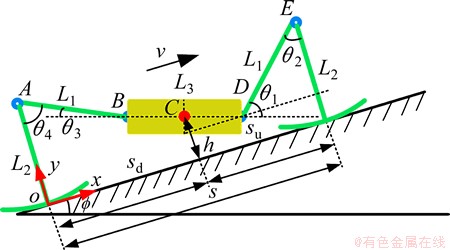
图2  八足仿蟹机器人行走机构简图

Fig.2  Walking mechanism diagram of a octopod crab-like robot

对简化后的机器人机构应用闭环矢量法^[14]得：

             (1)

式中：r_i代表从坐标系原点指向i点矢量；r_ij为从i点指向j点矢量；i和j分别指代图中的A，B，C，D和E点。

将式(1)中各矢量向图中坐标系的x和y轴上投影，可获得机器人的质心距站立面的高度h与各关节角度之间的关系：

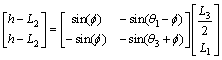    (2)

同理，机器人的质心在站立面的投影点至下坡向落足点和上坡向落足点的距离s_d和s_u可用式(3)求得：

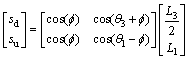     (3)

通过对式(2)和式(3)分析可知：机器人在斜面上行走时，机体质心距斜面的高度h和前后支撑落足点间的跨距s由斜面的倾斜角度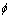、机体与股节的夹角θ₁和θ₃共同决定。

3  稳定性分析

当八足仿蟹机器人处于行走状态下，其运动速度较低，通常可以忽略躯体动能对稳定性的影响，在分析机器人行走稳定性时，可采用规范化的能量稳定裕度(NESM)来判定其稳定性。即用机器人绕给定转轴旋转到临界稳定位置时质心点垂直方向上的高度变化量来表征机器人的稳定裕度，如图3所示。

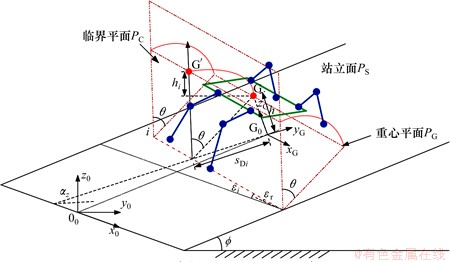
图3  八足仿蟹机器人静态稳定裕度计算简图

Fig.3  Calculation diagrams of static stability margin for a octopod crab-like robot

为了使表达更加明确，首先给出一些本文用到的一些专有名词的定义^[15]：

支撑面P_S为假想的机器人站立平面；旋转轴线i为由任意2个落足点连线形成的机器人可绕其翻滚的支撑边；重心平面P_G为由机器人重心与支撑边线所形成的平面；临界平面P_C为当稳定裕量为0时机器人重心与旋转轴边线所形成的平面；斜面倾角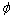为水平面与机器人的支撑平面之间夹角；质心高度h为机器人质心到支撑面的最短距离；旋转轴边水平倾角ε_i为旋转轴线在机器人支撑面内的投影与支撑面内水平线之间的夹角；旋转轴边垂直倾角ε_r为水平面与旋转轴线之间的夹角；支撑跨度s_Di为重心在支撑面内的投影点到支撑边线的最短距离；稳定裕度S_NESMij为表征机器人抵抗绕由i和j落足点形成的支撑边线翻滚的能力；稳定裕度S_NESMi为表征机器人抵抗绕支撑多边形第i个支撑边翻滚的能力。

多足机器人处于行走状态其空间姿态如图3所示，其中x₀，y₀和z₀为建立在大地上的全局坐标系；x_G，y_G和z_G为支撑面坐标系。机器人重心在支撑面内的垂直投影点作为该坐标系的原点， x_G轴与躯体纵轴方向相同，y_G沿机体的前进方向。当机器人多于3足处于支撑状态时，若运动路面不规则，则支撑足可能不处于同一平面，此时机器人的支撑面选择是使质心高度h保持最大。由图4中的几何关系可以求得机器人相对于任意支撑边i的S_NESMi为：

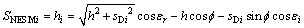(4)

式中：i表示某条支撑边，h_i为重心绕支撑边i转动到临界稳定位置时重心垂直高度的变化。

多足机器人在运动过程中步态稳定裕度可通过下式计算：

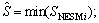i=1, 2, …, n        (5)

其中：n为机器人落地足所形成的支撑凸多边形的边数。

通过式(4)即可求得八足机器人的静态稳定裕度。在理想情况下，当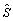为负数时，机器人处于不稳定状态，将出现倾翻；当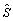等于0时，机器人处于临界稳定状态，由于在实际应用中一些机械误差和位置控制误差的存在，机器人在此状态下也很有可能失稳，因此，也将其认为不稳定状态；当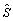大于0时，机器人处于稳定状态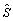，间接表征了机器人稳定的程度，称其为稳定裕度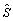，越大，机器人越稳定，抵抗扰动的能力也就越强。

3.1  八足机器人行走稳定性分析

由前面的理论分析可知：只要保持机器人的稳定裕量大于0，机器人即处于稳定状态。为了更好地对稳定性理论进行理解，给出一个具体的应用实例，本文以双四足步态沿斜面坡度方向横向行走为例分析八足机器人的行走稳定性(其他步态可以采用相同的研究方法)，将八足机器人的步行足从左前足开始按照逆时针的方向依次编号，采用双四足步态运动时8条步行足分为2组，步行足1，4，6和7为一组，步行足2，3，6和8为另一组，2组足交替抬起和落下，每一时刻都只有4条步行足处于支撑状态。运动中某一瞬时机器人重心和落足点投影图如图4所示，图中虚线为落地足所形成的支撑凸多边形。

由第2节运动学分析可知，当站立面倾角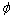已知，可求得机器人质心高度h与跨距s_d和s_u间的关系：

  (6)

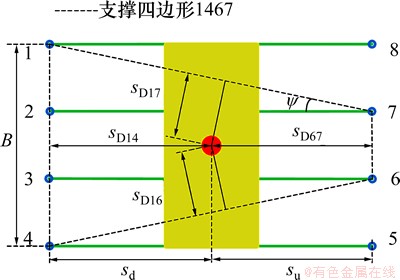
图4  双四足步态行走重心及落足点投影图

Fig.4  Projection figure of gravity center and touchdown points under walking of double tetrapod gait

对于由落足点1467所形成的支撑凸多边形如图4虚线所示，根据三角函数关系可求得：

      (7)

式中：s_Dij为质心投影点至由i，j落足点构成的支撑边的距离，i和j取值为1，4，6和7；B为机器人躯体的宽度。

当机器人在斜坡上沿坡度方向横行时，支撑面倾角为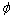，当以上下坡向支撑边线67或者14作为倾翻旋转边时，此时旋转边的垂直和水平倾角分别是：ε_r=0°和ε_i=0°。联立式(4)，(6)和(7)可得：

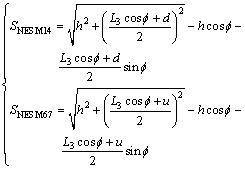   (8)

以侧向支撑边线17或者64作为倾翻轴边时，旋转轴垂直倾角ε_r的余弦值可通过式(9)求得：

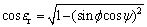          (9)

将式(4)，(6)，(7)和(9)联立可求得

           (10)

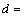
式中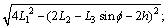： s=s_u+s_d。

由式(8)和(10)求得的最小值即为当前机器人的稳定裕量。从公式(8)和(10)可以看出：在机器人结构参数确定的情况下，稳定裕量与站立面的倾斜角度和机体质心的高度有关。

3.2  八足仿蟹机器人行走稳定性仿真与分析

随着斜面倾角和机体质心的变化，由式(8)和(10)还不能直观地获得机器人行走稳定性的变化趋势。为了定性得到八足机器人稳定裕度与斜面倾角和机体质心高度的关系，对其进行稳定性仿真。应用MATLAB软件对站立面倾斜角度从0°变化到35°，质心高度从70 mm变化到260 mm，机器人以双四足步态方式行走时的静态稳定裕度进行仿真得到如图5所示的曲线，其中图5(a)所示为相对于下坡向旋转轴14的稳定裕度S_NESM14和相对于上坡向旋转轴67的稳定裕度S_NESM67对比曲线。由图5可知：随着斜面坡度和质心高度的增加，机器人的稳定性降低，当机体高度小于某一值时(近似为157 mm)，相对于下坡向旋转轴14的稳定裕度大于相对于上坡向旋转轴67的稳定裕度，但当机体高度大于该值时，相对于下坡向旋转轴14的稳定裕量急剧下降，并小于相对于上坡向旋转轴67的稳定裕量。相对于侧向旋转轴17和64的稳定裕度曲线如图5(b)所示。综合图5(a)和5(b)分析可知：机器人的静态稳定裕度随着站立面倾角以及机体质心高度的增加而逐渐降低。

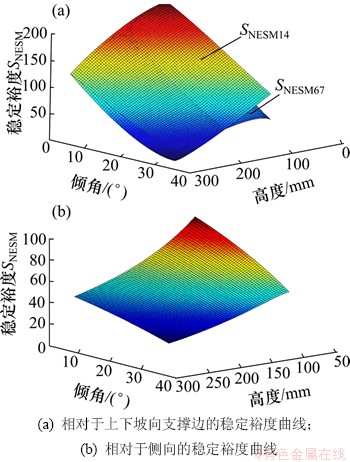
图5  四支撑足行走状态下稳定裕度曲线

Fig.5  Curve of stability margin under four support legged walking

4  实验研究

为验证前面理论研究和仿真结果的正确性，应用八足机器人实物样机搭建了一套机器人行走稳定性测试平台。将八足机器人放在可倾覆的木板上，以模拟不同地面倾角，使用dSPACE半物理仿真平台采集机器人足底的支撑力R，实验中机器人同样采用双足四足步态行走。在实验过程中使用拉力传感器在机器人质心的正上方平行于机体方向对机器人缓慢施加拉力F (施力点与质心的高度保持不变)，测量机器人足底支撑力的变化，当足底支撑力R=0时，说明机器人处于临界稳定状态，此时拉力传感器测量的拉力即为极限的扰动力，其值可以间接表征稳定程度：极限扰动力越大，表明机器人抵抗扰动的能力越强，也就是机器人越稳定。根据上述实验原理，对机器人进行稳定性实验，针对3种典型的行走坡度：(0°，15°和20°)，质心高度从70 mm到230 mm每隔20 mm测量1次。实验获得的不同质心高度下的极限扰动力曲线与仿真得到的S_NESM曲线对比如图6所示。分析图6中的实验曲线可知：随着质心的高度的增加，机器人的运动稳定性变差。当斜面倾角为0°时，机器人相对于上下坡向稳定性相同，因此极限扰动力曲线重合，实验和仿真获得的曲线近似一致；当斜面倾角不为0°，且质心高度小于某一临界值时，机器人相对于下坡向倾翻的稳定裕度大于上坡向倾翻的稳定裕量，质心的高度超过该临界值时相对于上坡向的倾翻的稳定裕量会大于下坡向的稳定裕量，2种不同坡度的临界质心高度值分别为160 mm和220 mm，与数值分析获取的157 mm略有不同。偏差的出现主要是实验中存在的一些误差造成的，但是整体趋势是一致的，验证了临界质心高度的存在。对比6(a)，6(b)和6(c)可以看出：机器人在0°，15°和20°斜坡上的最大极限扰动力分别为75，70和50 N，可知随着站立面倾斜角度的增加，机器人的稳定性是逐渐降低的，与数值分析获得结果相同。图6中样机实验结果与MATLAB仿真结果的特性基本吻合，从而验证了本文提出的稳定性判定方法的正确性。

5  结论

1) 为了准确评价仿蟹机器人的运动稳定性，通过对圆弧式足端结构的八足机器人整体运动学分析，应用规范化能量稳定裕度判据，提出了八足机器人在各种复杂环境下静态稳定的数学描述方法。

2) 针对八足生物常采用的双四足步态行走方式下的机器人稳定裕度进行了分析研究，得出了静态稳定裕度与机器人站立面倾角、机体高度的函数关系，并证明了临界质心高度的存在。

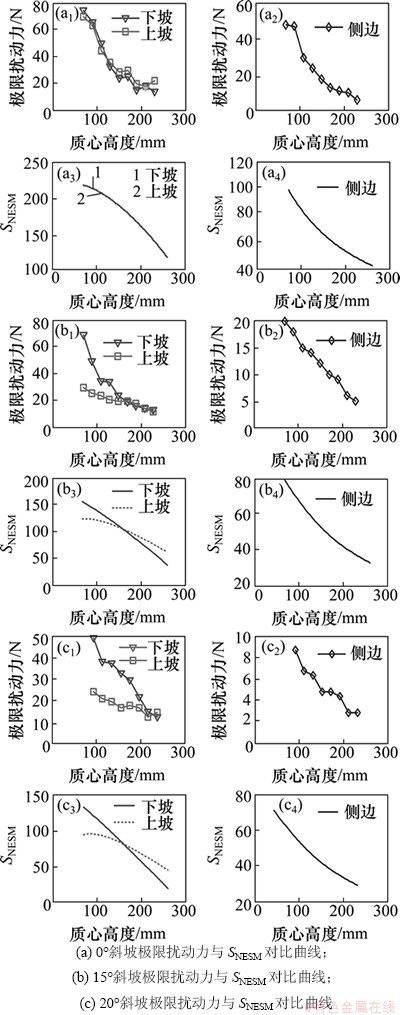
图6  不同质心高度极限扰动力与S_NESM曲线

Fig.6  Limit disturbance force and S_NESM curve of different centroid heights

3) 八足机器人静态稳定裕度数学计算方法简单、有效，能够准确判定仿蟹机器人运动过程中稳定性及稳定裕量变化。该稳定性判定方法为研究多足仿生机器人在复杂地貌环境下的行走方式以及失稳状态下的姿态恢复技巧提供了依据。

参考文献：

[1] Hirose S, Tsukagoshi H, Yoneda K. Normalized energy stability margin and its contour of walking vehicles on rough terrain[C]// Proceedings of the 2001 IEEE International Conference on Robotics and Automation, Seoul, Korea, 2001: 181-186.

[2] 黄俊军, 葛世荣, 曹为. 多足步行机器人研究状况及展望[J]. 机床与液压, 2008, 36(5): 187-191.

HUANG Junjun, GE Shirong, CAO Wei. Multi-feet walk robot research and its forecast[J]. Machine Tool& Hydraulics, 2008, 36 (5): 187-191.

[3] 陈甫, 藏希喆, 闫继宏, 等. 适合航行的六足仿生机器人Spider的研制[J]. 吉林大学学报(工学版), 2011, 41(3): 765-770.

CHEN Fu, ZANG Xizhe, YAN Jihong, et al. Development of navigable hexapod biomimetic robot spider[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(3): 765-770.

[4] 李斌, 刘金国, 谈大龙. 可重构模块机器人倾翻稳定性研究[J]. 机器人, 2005, 27(3): 241-246.

LI Bin, LIU Jinguo, TAN Dalong. Research on the tipover stability of a reconfigurable modular robot[J]. Robot, 2005, 27(3): 241-246.

[5] McGhee R B, Frank A A. On the stability properties of quadruped creeping gaits[J]. Mathematical Biosciences, 1968, 3(3): 331-351.

[6] Hardarson F. Stability analysis and synthesis of statically balance walking for quadruped robots[D]. Stockholm: Royal Institute of Technology, 2002: 47-65.

[7] Garcia E, Gonzalez P. An improved energy stability margin for walking machines subject to dynamic effects[J]. Robotica, 2005, 23 (1): 13-20.

[8] 王鹏飞, 黄博, 孙立宁. 四足仿生机器人稳定性判定方法[J]. 哈尔滨工业大学学报, 2008, 40(7): 1063-1066.

WANG Pengfei, HUANG Bo, SUN Lining. Stability judging method for quadruped bionic robot[J]. Journal of Harbin Institute of Technology, 2008, 40 (7): 1063-1066.

[9] 田海波, 方宗德, 周勇, 等. 轮腿式机器人倾覆稳定性分析与控制[J]. 机器人, 2009, 31(2): 159-165.

TIAN Haibo, FANG Zongde, ZHOU Yong, et al. Analysis and control for tumble stability of wheel-legged robot[J]. Robot, 2009, 31(2): 159-165.

[10] 王刚, 张立勋, 王立权. 仿蟹机器人交错等相位波形步态研究[J]. 机器人, 2011, 33(1): 237-243.

WANG Gang, ZHANG Lixun, WANG Liquan. On alternating equal-phase wave gait of crab-like robot[J]. Robot, 2011, 33(1): 237-243.

[11] 李林. 多足仿生机器蟹结构设计及实验研究[D]. 哈尔滨: 哈尔滨工程大学机电工程学院, 2010: 13-14.

LI Lin. The structure design and experimental study of the multi-legged bionic[D]. Harbin: Harbin Engineering University. College of Mechanical and Electrical Engineering, 2010: 13-14.

[12] 王刚, 张立勋, 王立权. 八足仿蟹机器人步态规划方法[J]. 哈尔滨工程大学学报, 2011, 32(4): 486-491.

WANG Gang, ZHANG Lixun, WANG liquan. Research on a gait planning method for a crab-like octopod robot[J]. Journal of Harbin Engineering University, 2011, 32(4): 486-491.

[13] 王洪波, 齐政彦, 胡正伟, 等. 并联腿机构在四足/两足可重组步行机器人中的应用[J]. 机械工程学报, 2009, 45(8): 24-30.

WANG Hongbo QI Zhengyan, HU Zhengwei, et al. Application of parallel leg mechanisms in quadruped/biped reconfigurable walking robot[J]. Journal of Mechanical Engineering, 2009, 45(8): 24-30.

[14] 于红英, 唐德威, 王建宇. 平面五杆机构运动学和动力学特性分析[J]. 哈尔滨工业大学学报, 2007, 39(6): 940-943.

YU Hongying, TANG Dewei, WANG Jianyu. Analysis of the kinematic and dynamic characteristics of a planar five-bar mechanism[J]. Journal of Harbin Institute of Technology, 2007, 39(6): 940-943.

[15] 许俊伟. 八足机器人步行机制及稳定性研究[D]. 哈尔滨: 哈尔滨工程大学机电工程学院, 2011: 40-41.

XU Junwei. Study on walking mechanism and stability of the eight-legged robot[D]. Harbin: Harbin Engineering University. College of Mechanical and Electrical Engineering, 2011: 40-41.

(编辑  何运斌)

收稿日期：2013-10-23；修回日期：2013-12-30

基金项目(Foundation item)：国家自然科学基金资助项目(60875067)；黑龙江省自然科学基金重点资助(ZD200911)项目(Project (60875067) supported by the National Natural Science Foundation of China; Project (ZD200911) supported by the Natural Science Foundation of Heilongjiang Province, China)

通信作者：王海龙(1988-)，男，黑龙江富锦人，博士研究生，主要从事多足仿生机器人的研究；电话：13654525356，E-mail：wanghailong@hrbeu.edu.cn

摘要：为准确评定新型圆弧形足端结构的八足机器人行走稳定性及稳定裕量，提出1种适用于八足机器人行走稳定性判定方法。对八足机器人整体结构进行抽象简化；使用闭环矢量法获得了质心与落足点之间的相对位置关系；应用规范化能量稳定裕度(S_NESM)方法对八足机器人静态稳定性进行描述，建立复杂环境下机器人静态稳定裕度的数学模型。通过数值仿真获得了机器人稳定裕度与机体质心高度及地面倾角之间的关系。稳定性实验结果表明：该方法能够准确判定八足机器人的行走稳定性。