
![]()

Trans. Nonferrous Met. Soc. China 22(2012) 1452-1456
Simulation of microstructures in solidification of aluminum twin-roll casting
CHEN Shou-dong1,2, CHEN Jing-chao1,2
1. Key Laboratory of Advance Material of Rare Precious and Nonferrous Metals of Ministry of Education,
Kunming University of Science and Technology, Kunming 650093, China;
2. Key Laboratory of Advanced Materials of Yunnan Province, Kunming 650093, China
Received 29 June 2011; accepted 15 November 2011
Abstract:
Based on the research on the solidification of twin-roll continuous casting aluminum thin strip, the analytical model of heterogeneous nucleation, the growth kinetics of tip (KGT) and columnar dendrite transformation to equiaxed dendrite (CET) of twin-roll continuous casting aluminum thin strip solidification was established by means of the principle of metal solidification and modern computer emulational technology. Meantime, based on the cellular automaton, the emulational model of twin-roll continuous casting aluminum thin strip solidification was established. The foundation for the emulational simulation of twin-roll casting thin strip solidification structure was laid. Meanwhile, the mathematical simulation feasibility was confirmed by using the solidification process of twin-roll continuous casting aluminum thin strip.
Key words:
twin-roll continuous casting; solidification structure; emulational simulation; micro-model;
1 Introduction
The twin-roll continuous casting thin strip is regarded as the most prospective technology of near-net-shape casting. Twin-roll strip continuous casting may save energy and manufacturing cost by eliminating some of the intermediate stages [1-7]. Furthermore, it can produce good properties due to high cooling rate.
Previous investigations [3] indicated that the solidification structure of twin-roll continuously cast thin strip, especially the crystal zone proportion, has an obvious effect on the thin strip quality. The control of the grain structure is of primary importance in twin-roll continuous cast strip because the solidification microstructure has a great influence on the quality and mechanical properties of strips. The microstructures of thin strip depend on the casting process parameters, and the microstructure has a great impact on its properties [8-11]. It is very necessary to investigate the effects of processing factors on the solidification structure zone of twin-roll continuously cast thin strips, such as pouring temperature, casting velocity and molten pool height. Considering that the matching degree among processing factors of twin-roll continuous casting is very complex, if experimental method is used to investigate the effects, the expense and work load are very high. Oppositely, if numerical simulation method is adopted, the expense and work load are relatively low.
In this study, a simple micro mathematical model was performed to simulate the solidification structure of twin-roll continuously cast thin strip. Then the influence of the casting conditions on the micro structure in solidification of strip was investigated in detail. Based on the micro mathematical model, the average grain size and the average columnar crystal deviation for twin-roll continuously cast aluminum thin strip are investigated and analyzed.
2 Microscopic model
2.1 Nucleation model
The continuous nucleation model [12] is employed in the present study, based on the following assumptions: 1) the fragmentation of dendrites and the oxidation of melt surface are neglected; 2) the effect of convection on nucleation is not considered. In the model, the density of grains, n(ΔT), formed at any undercooling ΔT, is given by:
 (1)
(1)
where ΔTN is the mean nucleation undercooling; ΔTσ is the standard deviation; and nmax is the maximum density of nuclei.
2.2 Growth kinetics model
In general, the constrained dendrite tip growth during rapid solidification was described by the Kurz-Giovanola-Trivedi (KGT) model [13]. However, it is well known that the twin-roll casting is a near-rapid solidification process thus the dendrite growth rate is not very high, and the growth dynamics coefficient is very large. Therefore, it is necessary to modify the model according to the solidification characteristics of twin-roll continuous cast thin strip. The modified KGT model is given as:
![]() (2)
(2)
where vtip is the growth rate of a dendrite tip at a certain undercoding, α and β are the empirical constants.
2.3 Columnar to equiaxed transition (CET)
In general, after the molten metal is poured into the gap between the rolls, the nucleation will appear on the surface of rolls, and then many nuclei form. Since there is a forced heat stream on the surface of rolls, these nuclei will preferentially grow in the opposite direction of the forced heat stream. There will be internal nucleation when the liquid phase temperature of columnar crystals front achieves interior nucleation temperature Ti. According to the theory proposed by FLOOD and HUNT [14], in afterward solidification process, the dendrite growth will transform from columnar to equiaxed growth. The CET model is given as follows.
Center equiaxial crystal:
![]() (3)
(3)
Equiaxed-columnar crystal:
![]() (4)
(4)
Columnar crystal:
![]() (5)
(5)
![]() (6)
(6)
where f1=0.49, f2=0.0049; n(t) is the grain density at each time-step; Re(t) is the mean radius of equiaxed grain at each time-step; fi(t) is the internal solid fraction at each time-step, which can be expressed as fi(t)=Ω(t), where Ω(t) is the solutal supersaturation of dendrite tip at each time-step.
All the control equations of twin-roll continuous casting, such as nucleation, equiaxed and columnar grain growth model, are shown as equations (1)-(6). Such as size of the equiaxed, columnar grain length and the process parameters affecting the solidification microstructure were achieved by certain calculations.
3 Computer emulational simulation of structures in solidification based on CA
According to the cellular automata model proposed by RAPPAZ and GANDIN [12], it may realize the kinetic simulator demonstration of the solidification structures in twin-roll continuous cast thin strip.
The freezing area is divided into quadrilateral or hexagonal grids, then each grid cell is divided into finer and uniform nodes, and all nodes before solidification is liquid (Pi=0). When the cell temperature is lower than the liquidus, in a time step δt, the temperature decreases by δT, and the undercooling increases by δΔT(δΔT>0). The new density of the nucleation in melt is given as:
![]() (7)
(7)
These new grains are randomly distributed in the whole CA unit, and the probability is
![]() (8)
(8)
where nv is the density of nuclei; δnv is the density of nuclei each-time; VCA is the volume of single CA unit; Pv is the volume nucleation on all CA units. Each CA unit is given one random number r (0≤r≤1) in every time-step δt. If a unit is still liquid whose state index remains at 0, when r≤Pv, the solid-liquid phase transition occurs, and its state index would be given a positive integer to describe the different grain orientations. When the CA unit nucleates, it will grow with a certain law. In numerical calculation, the approaches are as follows: A is a nucleation site in mesh grids which is nucleated at a certain time tA, and θ is the angle between the largest grain growth direction and x-axis. At time t, the radius of grain L(t) is the integral of growth velocity of dendrite tip in the whole growing time.
![]() (9)
(9)
where the growth pattern of dendrite tip (v[ΔT(t ')]) can be obtained by KGT model.
The sketch map of cellular automaton model is shown in Fig. 1. At the time tB, the grain A grows and touches the four neighboring cells B1, B2, B3 and B4. At this time, the semi-diagonal of grain LtB is equal to lθ=(cosθ+|sinθ|), where l is the distance between two CA mesh grids. CA model prescribes that B1, B2, B3 and B4 are considered to become solid and assigned a crystallographic index as the same as A. The grain continues to grow and capture the neighboring liquid sites and form the final grain shape. B1, B2, B3 and B4 continue to grow and capture the eight sites of neighboring C at the next time. The grain increases with the growth velocity of dendrite tip.
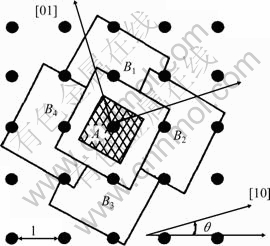
Fig. 1 Sketch map of cellular automaton model
4 Validation of mathematical model
The aluminum thin strip was chosen to validate the mathematical model. We may simplify the twin-roll continuous casting process of thin strip as the two-dimensional problem. The primary technical parameters of twin-roll casting are listed in Table1. The thermo physical properties of aluminum needed for the model are listed in Table 2.
To reduce the calculation time, the computing region of solidification process should be simplified as a micro-unit (cube), whose dimensions are 0.5 mm×0.5 mm×1 mm. The model of simulation on solidification process of twin-roll continuous casting strip is shown in Fig. 2. The twin-roll continuous cast aluminum thin strip with the thickness of 6.0 mm was produced in the experiment. The simulated and experimental results of solidification microstructure of twin-roll continuous cast aluminum thin strip at the casting speed of 0.8 m/min and under the conditions of pouring temperature of 690 ℃, melt pool height of 70 mm are shown in Figs. 3 and 4.
Table 1 Production condition and main parameters of twin-roll strip casting

Table 2 Thermo-physical properties of aluminum [15]
By analysis, the average grain size and the average columnar crystal deviation were measured, and the results are shown in Fig. 5. As a comparison, the predicted results of mathematical model are also shown in Fig. 5.
It is found from Figs. 4 and 5 that the predicted results are relatively consistent with the measured ones, indicating that the mathematic model is reliable thus can be used to predict the effects of processing parameters on the solidification structure of twin-roll continuous cast thin strips.
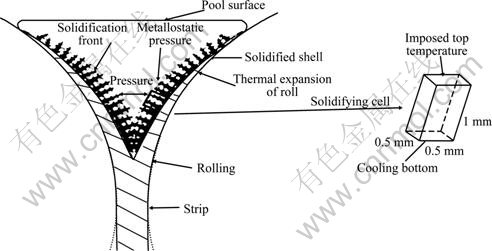
Fig. 2 Schematic of model of simulation on solidification process of twin-roll continuous cast thin strip

Fig. 3 Simulated results of solidification microstructure of twin-roll continuous cast aluminum thin strip at casting speed of 0.8 m/min under conditions of pouring temperature of 690 ℃, melt pool height of 70 mm: (a) t=5 s; (b) t=10 s

Fig. 4 Microstructures of twin-roll continuous cast aluminum thin strip: (a) Solidified organization on cross section of aluminum strip; (b) Local magnification of (a)
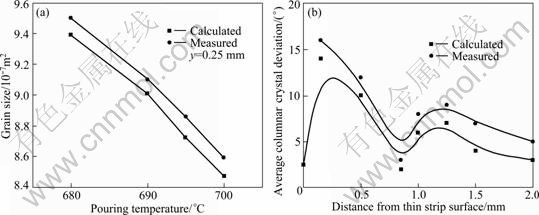
Fig. 5 Average grain size (a) and average columnar crystal deviation (b) of twin-roll continuous cast aluminum strip
5 Conclusions
1) A simple micro mathematical model for solidification structure simulation of twin-roll cast thin strip is developed. In the model, the latent heat is treated with the enthalpy method. Moreover, the heterogeneous nucleation model, cellular automaton model and columnar-to-equiaxed transition models are also introduced, together with the revising of dendrite growth dynamic model of KGT. Although the predicted results of the micro mathematical model are relatively consistent with the measured ones, some errors still exist due to many assumptions in the model.
2) The average grain size and the average columnar crystal deviation were measured. The predicted results of the micro mathematical model are relatively consistent with the measured ones. It is shown that the established micro mathematical model is reliable, and it can predict influence of parameters on solidification structure of twin-roll continuous cast thin strip. The numerical simulation can provide some theoretical guidance for twin-roll continuous cast thin strip.
References
[1] WANG Bo, ZHANG Jie-yu, LI Xiang-mei, QI Wei-hua. Simulation of solidification micro structure in twin-roll casting strip [J]. Computational Materials Science, 2010, 49: s135-s139.
[2] YANG Ming-bo, PAN Fu-sheng. Analysis about forming mechanism of equiaxed crystal zone for 1Cr18Ni9Ti stainless steel twin-roll thin strip [J]. Journal of Materials Processing Technology, 2009, 209: 2203-2211.
[3] GRAS C, MEREDITH M, HUNT J D. Micro structure and texture evolution after twin roll casting and subsequent cold rolling of Al–Mg–Mn aluminum alloys [J]. Journal of Materials Processing Technology, 2005, 169: 156-163.
[4] YUCEL B. Analysis of macro segregation in twin-roll cast aluminum strips via solidification curves [J]. Journal of Alloys and Compounds, 2009, 486: 168-172.
[5] SANJEEV D, LIM N S, SEOL J B, KIM H W, PARK C G. Effect of the rolling speed on micro structural and mechanical properties of aluminum–magnesium alloys prepared by twin roll casting [J]. Materials and Design, 2010, 31: 1633-1638.
[6] YUCEL B. The performance of Al–Ti–C grain refiners in twin-roll casting of aluminum foilstock [J]. Journal of Alloys and Compounds, 2007, 430: 179–187.
[7] SANTOS C A, SPIM J A Jr, GARCIA A. Modeling of solidification in twin-roll strip casting [J]. Journal of Materials Processing Technology, 2000, 102: 33-39.
[8] MIAO Yu-chuan, ZHANG Xiao-ming, DI Hong-shuang, WANG Guo-dong. Numerical simulation of the fluid flow, heat transfer, and solidification of twin-roll strip casting [J]. Journal of Materials Processing Technology, 2006, 174: 7–13.
[9] ZENG J, KOITZSCH R, PFEIFER H, FRIEDRICH B. Numerical simulation of the twin-roll casting process of magnesium alloy strip [J]. Journal of Materials Processing Technology, 2009, 209: 2321–2328.
[10] SPINELLI J E, TOSETTI J P, SANTOS C A, SPIM J A, GARCIA A. Micro structure and solidification thermal parameters in thin strip continuous casting of a stainless steel [J]. Journal of Materials Processing Technology, 2004, 150: 255–262.
[11] LIU H T, LIU Z Y, QIU Y Q, CAO G M, LI C G, WANG G D. Characterization of the solidification structure and texture development of ferritic stainless steel produced by twin-roll strip casting [J]. Materials Characterization, 2009, 60: 79-82.
[12] RAPPAZ M, GANDIN C A. Probabilistic modeling of micro structure formation in solidification process [J]. Acta Metall, 1993, 41: 345-352.
[13] KURZ W, GIOVANOLA B, TRIVEDI R. Theory of micro structural development during rapid solidification [J]. Acta Metall, 1986, 34: 823-830.
[14] FLOOD S C, HUNT J D. Columnar and equiaxed growth. I. A model of a columnar front with a temperature dependent velocity [J]. J Cryst Growth, 1987, 82: 543-552.
[15] WANG Zhu-tang, TIAN Rong-zhang. Manual processing of aluminum and its alloy [M]. Changsha: Central South University of Technology Press, 1989: 153-154. (in Chinese)
铝双辊连续铸轧凝固微观组织的数值模拟
陈守东1,2,陈敬超1,2
1. 昆明理工大学 稀贵及有色金属先进材料教育部重点实验室,昆明 650093;
2. 云南省新材料制备与加工重点实验室,昆明 650093
摘 要:在研究双辊连铸纯铝薄带凝固过程的基础上,基于金属凝固的基本原理,并运用现代计算机仿真技术建立双辊连续铸轧纯铝薄带凝固的异质形核,枝晶尖端的生长动力学(KGT),柱状晶向等轴晶生长的转变(CET)的解析模型;建立基于元胞自动机(CA)的双辊连铸纯铝薄带凝固组织的仿真模型,为双辊连铸薄带凝固组织的仿真模拟奠定基础,从而为双辊薄带连铸工艺提供一定的理论指导。同时,利用双辊薄带连续铸轧纯铝凝固微观组织过程验证数学模拟的可行性。
关键词:双辊连续铸轧;凝固组织;仿真模拟;微观模型
(Edited by LI Xiang-qun)
Foundation item: Project (u0837601) supported by the New Joint Fund of National Natural Science Foundation of China; Project (50874054) supported by the National Natural Science Foundation of China
Corresponding author: CHEN Jing-chao, Tel: +86-871-5189490; E-mail: cjingchao@hotmail.com
DOI: 10.1016/S1003-6326(11)61340-X
Abstract: Based on the research on the solidification of twin-roll continuous casting aluminum thin strip, the analytical model of heterogeneous nucleation, the growth kinetics of tip (KGT) and columnar dendrite transformation to equiaxed dendrite (CET) of twin-roll continuous casting aluminum thin strip solidification was established by means of the principle of metal solidification and modern computer emulational technology. Meantime, based on the cellular automaton, the emulational model of twin-roll continuous casting aluminum thin strip solidification was established. The foundation for the emulational simulation of twin-roll casting thin strip solidification structure was laid. Meanwhile, the mathematical simulation feasibility was confirmed by using the solidification process of twin-roll continuous casting aluminum thin strip.


