非线性准则下多孔岩土体弹塑性变形推导与数值模拟

黄林冲¹，徐进²，周翠英¹，程晔¹

(1. 中山大学 工学院，广东 广州，510275；

2. 中南大学 土木建筑学院，湖南 长沙，410075)

摘 要：

摘  要：基于临界状态塑性模型，针对多孔岩土材料，从非线性的弹性本构方程出发，对其率形式进行积分求解，得到弹性行为下切线应力-应变模量的表达式；在此基础上，引入一致性系数，对非线性准则下弹塑性变形本构方程的增量形式进行应力积分求解；编制大型有限元计算程序以及积分求解核心算法程序，再现饱和砂土边坡液化的形成过程。研究结果表明：在边坡局部剪切带即将形成的区域，孔隙水压力明显增大，而且沿着剪切带的外法线方向向外流动；在远离剪切带区域，水压力分布较均匀，且流动方向趋于水平；根据液化发生准则，得到了边坡发生液化的滑动面。

关键词：

非线性准则；弹塑性变形；多孔岩土材料；数值计算；

中图分类号：TU441.35          文献标志码：A         文章编号：1672-7207(2010)05-1900-06

Elasto-plastic deformation derivation and numerical simulation of pore geo-material by non-linear law

HUANG Lin-chong¹, XU Jin², ZHOU Cui-ying¹, CHENG Ye¹

(1. School of Engineering, Sun Yat-sen University, Guangzhou 510275, China;

2. School of Civil and Architectural Engineering, Central South University, Changsha 410075, China)

Abstract: Based on the critical state plasticity model, an integration algorithm of the rate form for the non-linear elastic constitutive equations was performed to gain the tangent stress-strain of the elastic behavior; then the coincidence coefficient was introduced to calculate the incremental form of the elasto-plastic deformation constitutive equations under non-linear law. At last, a finite element program and an integration algorithm were coded by FORTRAN to simulate the onset of the liquefaction of a sand slope. The results show that the pore pressure affects the onset and development of the deformation band greatly, and the pore pressure increases around the localization-prone regions obviously with the direction toward the outer side of the normal of the shear band, while the pore stress flows nearly horizontally and is distributed equality far away from the shear band region. The sliding surface of the slope can be derived when the liquefaction happened, according to the law of the onset of liquefaction.

Key words: non-linear law; elasto-plastic deformation; pore geo-material; numerical calculation

由于多孔介质三相状态的复杂性，在一般情况下很难得到其弹塑性变形的解析解^[1]。在求解过程中，有限元法是最常用的数值分析方法。自20世纪40年代开始，Biot^[2-4]讨论了液饱和多孔介质的基本模型，引进了液体和固体间的相对运动耗散和惯性耦合。Terzaghi等^[5-6]对Biot多孔介质模型的有限元数值分析进行了研究，给出了不同变量表示的几种不同形式的有限元方程。Lewis等^[7-9]也在Terzaghi和Biot理论的基础上通过改进单元、引入梯度塑性和内尺度律等理论，进一步发展了多孔介质的有限元数值分析及其应用。尽管Biot模拟得到了广泛的应用，但由于其源自经验，缺乏充分的力学依据，存在不足。基于连续介质力学的混合物理论的建立，导致现代多孔介质理论的出现。现代多孔介质理论被认为是受体积分数约束的混合物理论^[10]。Andrade等^[11]在现代连续介质力学框架内，以混合物理论为基础，将体积分数视为独立变量，给出了不可压缩和可压缩液体饱和多孔介质模拟。在此基础上，Borja等^[10-11]从非线性准则出发，建立了液相、气相和固相状态下的多孔介质的临界状态塑性模型。对于多孔介质，尤其对于多孔岩土体材料，不仅有可恢复的弹性变形，更多地表现为不可恢复的塑性变形。为此，本文作者基于Borja等^[10]建立的临界状态塑性模型，对多孔介质材料进行弹塑性变形的积分求解，编制大型有限元计算程序，以实现有限元数值模拟。

1  非线性准则下弹性本构方程求解

基于Borja等^[11]建立的临界状态塑性模型，从非线性的弹性本构方程出发，对其本构方程的率形式进行积分：

              (1a          ndary以及动量守恒方程的拉格朗日形式；)

式中：上标e和p分别代表弹性和塑性；符号“:”表示2个正二阶张量的内积；符号“”表示“”对时间的导数。

        (2a          ndary以及动量守恒方程的拉格朗日形式；)

1为2阶恒等张量；K和分别为弹性体积模量和剪切模量。同时，假设它们都与压力p线性相关，并满足^[11]：

，           (3a          ndary以及动量守恒方程的拉格朗日形式；)

E为固相的孔隙率；为膨胀系数；为弹性泊松比。

将式(1)写成如下形式：

，           (4a          ndary以及动量守恒方程的拉格朗日形式；)

式中：

，    (5a          ndary以及动量守恒方程的拉格朗日形式；)

假设泊松比是常量，那么也为常量。对式(4)进行对时间的积分可得到：

    (6a          ndary以及动量守恒方程的拉格朗日形式；)

式中：；；代表固相矩阵中的“平均”体积刚度。

从(6)式可推导得：

     (7a          ndary以及动量守恒方程的拉格朗日形式；)

计算式(4)的体积部分，结合式(3)可得：

              (8a          ndary以及动量守恒方程的拉格朗日形式；)

对式(8)积分得：

           (9a          ndary以及动量守恒方程的拉格朗日形式；)

比较式(7)和式(9)，得：

        (10a          ndary以及动量守恒方程的拉格朗日形式；)

将式(10)代入式(6)，有：

   (11a          ndary以及动量守恒方程的拉格朗日形式；)

式(10)中是一个时间增量内割线体积弹性模量的近似值，因此，是非线性弹性张量的割线近似值，它们各自的含义如图1~2所示。

图1  割线和切线体积弹性模量

Fig.1  Bulk elastic modulus of secant line and tangent line

图2  割线弹性张量

Fig.2  Elastic tensor of secant line

对于弹性变形，，，因此，式(11)能够由给定的完全应变增量直接求解。但是，式(11)仅仅表示的是近似值，并不代表本构方程形式的准确解析积分。与式(11)相协调的切线应力-应变张量可以通过式(6)求导得到：

    (12a          ndary以及动量守恒方程的拉格朗日形式；)

式中：上标k表示迭代数。与相关的变量为：

，，

   (13a          ndary以及动量守恒方程的拉格朗日形式；)

对于弹性行为，其切线应力-应变模数可表示为：

         (14a          ndary以及动量守恒方程的拉格朗日形式；)

可以看出：即使在非线性弹性形变下，依然需要进行迭代求解。

2  非线性准则下弹塑性本构关系求解

在弹塑性模型中，其变形由弹性和塑性2部分组成，即。

令，，，则的体积分量为：；其偏量分量为： (其中，代表前面n个时间步长的收敛应变张量)。

以和分别代表的弹性和塑性部分，则有：

          (15aa          ndary以及动量守恒方程的拉格朗日形式；)

            (15ba          ndary以及动量守恒方程的拉格朗日形式；)

         (15ca          ndary以及动量守恒方程的拉格朗日形式；)

根据流动法则，其塑性应变增量通过隐式计算得到：

     (16a          ndary以及动量守恒方程的拉格朗日形式；)

式中：，，， ＞0表示一致性系数，屈服方程F为：

          (17a          ndary以及动量守恒方程的拉格朗日形式；)

其中：p_c为预固结压力。从而塑性应变增量的体积分量和偏量分量分别由下式决定：

    (18aa          ndary以及动量守恒方程的拉格朗日形式；)

     (18ba          ndary以及动量守恒方程的拉格朗日形式；)

2.1  应力积分算法

与前面所介绍的弹性行为相似，对于塑性行为，增量形式的本构方程可参照式(11)写成如下形式：

    (19a          ndary以及动量守恒方程的拉格朗日形式；)

从而可计算得到的体积分量和偏量分量为：

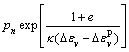          (20aa          ndary以及动量守恒方程的拉格朗日形式；)

式中：；。

          (20ba          ndary以及动量守恒方程的拉格朗日形式；)

式中：

       (21a          ndary以及动量守恒方程的拉格朗日形式；)

，表示时间步长内的剪切模量的平均值。

由式(18ba          ndary以及动量守恒方程的拉格朗日形式；)可知：取值依赖于。结合式(21)，可得到：

       (22a          ndary以及动量守恒方程的拉格朗日形式；)

从而，在有限时间增量内，

  (23a          ndary以及动量守恒方程的拉格朗日形式；)

    (24aa          ndary以及动量守恒方程的拉格朗日形式；)

增量形式的硬化准则可以用以下的指数形式表 示^[12]：

     (24ba          ndary以及动量守恒方程的拉格朗日形式；)

式中：。

硬化方程的率形式为：。

2.2  一致性系数的求解

注意到上面的的体积分量和偏量分量都与有关，下面将求解一致性系数。

结合相容方程(17)以及式(23a          ndary以及动量守恒方程的拉格朗日形式；)与(24a          ndary以及动量守恒方程的拉格朗日形式；)可知：

       (25a          ndary以及动量守恒方程的拉格朗日形式；)

设立初始值，，， ，联立非线性方程组(23a          ndary以及动量守恒方程的拉格朗日形式；)、(24a          ndary以及动量守恒方程的拉格朗日形式；)和(25a          ndary以及动量守恒方程的拉格朗日形式；)，通过牛顿迭代求出根值，，以及。

3  有限元数值模拟实现

基于以上的弹塑性变形的积分推导，结合有限元理论，编制了FORTRAN 环境下的大型有限元数值分析程序以及大型刚度矩阵积分求解的算法程序，实现多孔介质变形的有限元数值分析。下面应用该大型有限元分析程序以及积分求解的核心程序模拟并分析某饱和砂土边坡液化形成时的力学状态。

3.1  计算模型

计算模拟的边坡尺寸如图3所示，边坡高为10 m，坡度为30?，水平面距边坡顶面5 m。计算网格为二维四边形Q9P4等参单元，计算模型如图4所示。每个Q9P4单元中有9个位移节点和4个连续孔隙水压力节点，这种单元能够很好地满足 Babuska-Brezzi稳定性条件，从而避免由于多孔介质的固结而引起的稳定性问题^[12-13]。Q9P4单元示意图如图5所示。计算边界条件是：模型下部、左右两侧为铰接固定支座，上部(包括边坡部分)为自由条件；同时，模拟中采用预压固结应力100 kPa的静力加载。加载时间-加载因子曲线如图6所示。

图3  计算模型的几何尺寸和边界条件

Fig.3  Geometrical dimension and boundary condition of computational model

图4  计算模型

Fig.4  Computational model

图5  Q9P4单元示意图

Fig.5  Schematic diagram Q9P4 element

图6  加载时间-加载因子曲线

Fig.6  Curve of load time vs load factor

3.2  计算参数

进行数值模拟的试件材料的主要计算参数如表1所示。

表1  材料的计算参数

Table 1  Values of material parameters

3.3  计算结果与分析

Borja等^[10-11]给出了硬化模量H以及临界硬化模量H_crit的表达式，并指出当H=H_crit时，开始出现液化现象。根据这个判据，得到此处边坡发生局部变形产生液化的力学状态。

图7所示为边坡发生液化时的水压力分布图，其中，白色箭头为水压力的流动方向。从图7可以看出：流体对于这种颗粒状介质的力学行为影响较大，在边坡中心处的水压力最大，尤其是靠近边坡顶面位置尤为明显，达到280 kPa左右；在剪切带即将形成的区域，孔隙水压力明显增大，而且沿着剪切带的外法线方向向外流动；在远离剪切带区域，水压力分布较均匀，且流动方向趋于水平。

图8所示为边坡液化发生时叠加流体向量的偏应变云图。从图8可以看出：在整个斜坡坡面的偏应变

图7  水压力分布图

Fig.7  Contour of pore pressure

图8  叠加流体向量的偏应变云图

Fig.8  Deviatoric strains in contour with superimposed flow vector

最大，超过了0.25%，因此，该坡面处于不稳定的状态。和水压力分布相似的是，在边坡的中心，尤其靠近边坡顶面的位置，其偏应变也较大，而且与斜坡的局部变形带连成了一起，从而导致边坡体的液化变形。

图9所示为每个高斯点的H-H_crit。根据液化判断准则，当H-H_crit≤0时，液化发生。如图9所示，整个坡面以及靠近边坡顶部中心的部位都处于H- H_crit＜0的位置，因此，这些部位将是液化发生时坡面下滑的区域。这一结果与前面的水压力分布以及偏应变分布相吻合，证明在多孔类颗粒状介质中水压力对于其力学行为影响较大。图9中的虚线即为边坡发生液化的滑动面。

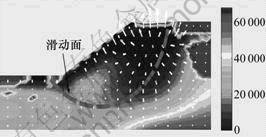
图9  各个高斯点的H-H_crit

Fig.9  H-H_crit of each Guass point

4  结论

(1) 在非线性准则下的弹塑性变形中，引入应力的体积分量、偏量分量以及一致性系数，得到了多孔介质弹塑性变形增量形式的积分求解。

(2) 在工程实际中，多孔介质一般涉及与流体耦合的问题，而且流体的流动与孔隙水压力对局部变形带的形成影响较大。

(3) 在多孔介质边坡的局部剪切带即将形成的区域，孔隙水压力明显增大，而且沿着剪切带的外法线方向向外流动；在远离剪切带区域，水压力分布较为均匀，且流动方向趋于水平。

(4) 根据液化发生准则，得到了边坡发生液化的滑动面，这对于预测边坡的发生具有重要的现实意义。

参考文献：

[1] HUANG Lin-chong, XU Zhi-sheng, WANG Li-chuan. Constitutive equations and finite element implementation of strain localization in sand deformation[J]. Journal of Central South University of Technology, 2009, 16(3): 482-487.

[2] Biot M A. General theory of three dimensional consolidation[J]. Journal of Applied Physics, 1941, 12(2): 155-164.

[3] Biot M A. Theory of propagation of elastic waves in a fluid saturated porous solid[J]. Journal of the Acoustical Society of America, 1956, 28(2): 168-178.

[4] Biot M A. Mechanics of deformation and acoustic propagation in porous media[J]. Journal of Applied Physics, 1962, 33(4): 1482-1498.

[5] Terzaghi K. Theoretical Soil Mechanics[M]. New York: John Wiley and Sons, 1943: 66-76.

[6] Simon B R, Wu S S, Zienkiewicz O C. Evaluation of u-w and u-π finite element methods for the dynamic response of saturated porous media using one-dimensional models[J]. International Journal for Numerical and Analytical, 1986, 10(5): 461-482.

[7] Lewis R W, Schrefeler B A. The finite element method in the static and dynamic deformation and consolidation of porous media[M]. Chichester: John Wiley and Sons, 1998: 93-94.

[8] 李锡夔, Cescotto S. 梯度塑性的有限元分析及应变局部化分析[J]. 力学学报, 1996, 28(5): 575-584.
LI Xi-kui, Cescotto S. Finite element analysis for gradient plasticity and modeling of strain localization[J]. Acta Mechanic Sinica, 1996, 28(5): 575-584.

[9] 张洪武, 张新伟. 基于广义塑性本构模型的饱和多孔介质应变局部化分析[J]. 岩土工程学报, 2000, 22(1): 23-29.
ZHANG Hong-wu, ZHANG Xin-wei. Generalized plastic constitutive model based on strain localization analysis of saturated porous media[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(1): 23-29.

[10] Borja R I, Andrade J E. Critical state plasticity, Part VI: Meso-scale finite element simulation of strain localization in discrete granular materials[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(37/40): 5115-5140.

[11] Andrade J E, Borja R I. Capturing strain localization in dense sands with random density[J]. International Journal for Numerical Methods in Engineering, 2006, 67(11): 1531-1564.

[12] Jefferies M G. Nor-Sand: a simple critical state model for sand[J]. Géotechnique, 1993, 43(1): 91-103.

[13] HUANG Lin-chong, XU Zhi-sheng, ZHOU Cui-ying. Modeling and monitoring in a soft argillaceous shale tunnel[J]. Acta Geotechnics, 2009, 4(4): 273-282.

(编辑 刘华森)

收稿日期：2009-10-11；修回日期：2009-12-26

基金项目：国家自然科学基金重点资助项目(41030747)；国家自然科学基金面上资助项目(40672194)；国家高技术研究发展计划(“863”计划)项目(2007AA11Z112)；中国博士后科学基金面上资助项目(20090460827)；广东省自然科学基金重点资助项目(06104932；013188)；高等学校博士学科点基金资助项目(20060558060；20090171110044)

通信作者：黄林冲(1981-)，男，湖北咸宁人，博士后，从事岩土工程和防灾安全研究；电话：020-84111124；E-mail: ueit@mail.sysu.edu.cn