J. Cent. South Univ. Technol. (2007)05-0701-07
DOI: 10.1007/s11771-007-0134-9 
Robustly stable model predictive control based on
parallel support vector machines with linear kernel
BAO Zhe-jing(包哲静)1, ZHONG Wei-min(钟伟民)2, PI Dao-ying(皮道映)1, SUN You-xian(孙优贤)1
(1. State Key Laboratory of Industrial Control Technology, Zhejiang University, Hangzhou 310027, China;
2. State Key Laboratory of Chemical Engineering, East China University of Science and Technology,
Shanghai 200237, China)
Abstract：Robustly stable multi-step-ahead model predictive control (MPC) based on parallel support vector machines (SVMs) with linear kernel was proposed. First, an analytical solution of optimal control laws of parallel SVMs based MPC was derived, and then the necessary and sufficient stability condition for MPC closed loop was given according to SVM model, and finally a method of judging the discrepancy between SVM model and the actual plant was presented, and consequently the constraint sets, which can guarantee that the stability condition is still robust for model/plant mismatch within some given bounds, were obtained by applying small-gain theorem. Simulation experiments show the proposed stability condition and robust constraint sets can provide a convenient way of adjusting controller parameters to ensure a closed-loop with larger stable margin.
Key words:
parallel support vector machines; model predictive control; stability; robustness；
1 Introduction
The use of support vector machine (SVM) in model predictive control (MPC) has received considerable attention. Several papers have appeared on SVM based MPC[1-5], all of which concentrate only on the issue related to constructing SVM model, combining SVM model with MPC and deriving the optimal solution[6]. Some papers applied the gradient descent based method to search the control laws, which cannot be ensured to be globally optimal[1-3], and others achieved an analytical solution of control laws[4-5]. However no attention is paid to the stability of the closed-loop system.
In MPC, while the performance of the plant is optimized over the prediction horizon repeatedly, each optimization does not care about what happens beyond the prediction horizon, and so the plant can be put into a state that it will eventually be impossible to stabilize, even though the controlled plant itself is stable[7-8].
In this paper, the structure block diagram of parallel SVMs based MPC closed loop was obtained. Due to linear kernel, classical theoretical results can be applied to analyze the stability of SVMs-MPC, and then according to SVM model the stability condition was derived. A method of judging the discrepancy between SVM model and the actual plant was proposed, and further the constraint sets for the discrepancy were given to ensure that the real closed-loop system is robustly stable.
2 Parallel SVMs with linear kernel based MPC algorithm
The structure of parallel SVMs based multi-step-ahead MPC is shown in Fig.1, in which Hp (prediction horizon) parallel SVMs predictive models constitute multi-step-ahead predictor, ys(k+j) is the desired set-point value of output y at time k+j, 
is the j-step-ahead predictive output at time
k after feedback correction,
is the Hp-step-ahead predictive output at time k-Hp after feedback correction, z-i and z-j are the delay operators. All sub-models do not influence each other, and then an accumulation of prediction errors can not occur.
Assume an unknown process can be described as follows:
(1)
where n≥1 and m≥1 are maximum lags in the outputs and inputs, respectively, and 
.
According to Eqn.(1) and 
,
we have
(2)
Repeat the procedure recursively and the 
-step-ahead predictor is yielded:
(3)
SVM with linear kernel can regress the unknown linear and weakly nonlinear system well. Using SVM regression technique, the model with linear kernel can be then represented as[9-10]:
(4)
where nsvj is the number of support vector of model; 
is the input vector of support vector corresponding samples of the model 
and
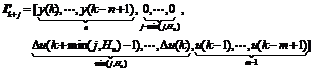
Now we can rewrite Eqn. (4) as follows:
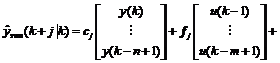
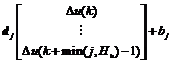(5)
where 
,
and
.
In MPC, the quadratic objective function is defined as[11]
(6)
where 
,
,
and the weighting matrices Q and R are given by 
and 
.
We propose that -step-ahead predictive model at time k should be corrected by the discrepancy between the latest plant output y(k) and the latest -step-ahead predictor output 
. So it holds
(7)
From Eqn. (5), it can be derived that:
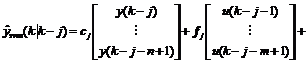
(8)
Then we can get
(9)
where
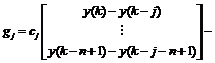
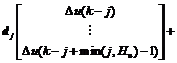
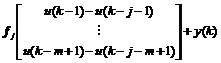(10)
So the following holds:
(11)
where 
and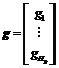 
.
The necessary condition for Eqn.(6) to have a minimum is to set 
, in which
.
Therefore the optimal control law is
(12)
where 
.
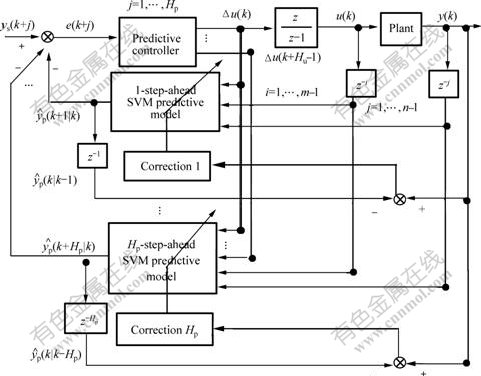
Fig.1 Diagram of parallel SVMs based MPC
3 Stability analysis of parallel SVMs with linear kernel based MPC
We can represent Eqn. (10) as 
.
where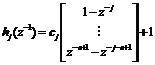 
and
.
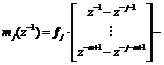
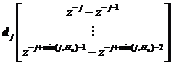So vector g can be rewritten as
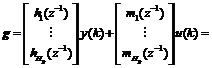
(13)
From Eqn. (5), SVM model has the form
(14)
where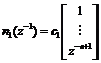 
,
and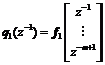
.
Eqn. (14) can be rewritten in z-transform form as
(15)
Define s(z-1)=p1(z-1)+q1(z-1) and t(z-1)=z-n1(z-1).
Theorem 1 According to SVM model of the controlled plant, parallel SVMs based MPC closed-loop system is stable if and only if all the roots of polynomial 
are inside the unit circle, where
(16)
Proof Since the controlled plant is unknown, we substitute SVM mode for the plant. Consequently, the structure of closed-loop system is shown in Fig.2.
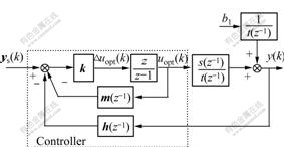
Fig.2 Structural diagram of closed-loop system
As shown in Fig.2, the SVMs-MPC closed loop has two inputs, one is ys(k) and the other is b1. Bias 
can be thought as a measurement noise. The transfer functions from ys(k) and b1 to output are respectively:
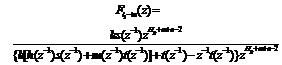
and
where 
is the transfer function from input 1(ys(k)) to output; 
is the transfer function from input 2(b1) to output.
The poles of transfer function from bias b1 to output y(k) are the same as those of transfer function from ys(k) to output y(k). From classical theory, the necessary and sufficient stability condition of the MPC closed-loop system is derived, that is, all the roots of polynomial G(z)=0 are inside the unit circle, where
Remark 1 From the stability condition, we can know that the stability is relevant to MPC parameters Hp, Hu, Q, R and SVM model. For a specific controlled plant, SVM model is determined, so stability can be achieved by adjusting MPC parameters.
4 Robust analysis of parallel SVMs with linear kernel based MPCUsually there exists modeling error or system perturbation, but the above mentioned stability condition is derived according to SVM model. Consequently for a closed-loop system composed of the controller and the actual plant, it is necessary to give the constraint sets, which can guarantee that the stability condition is still robust.
Without lose of generalization, Δ is employed to denote the discrepancy between SVM model and the actual plant, and then an additive uncertainty parameter is appended to the transfer function of SVM model, that is
(17)
where Pactual is the actual transfer function of the controlled plant, Δ is assumed to be stable and 
.
Theorem 2 The closed-loop system, composed of the controller designed by the stability condition in Theorem 1 and the actual controlled plant with uncertainty, will remain robustly stable if
(18)
where 
denotes the largest singular value and 
.
Proof By considering the system uncertainty as in Eqn.(17) and omitting inputs, the structure of SVMs-MPC and the plant with additive uncertainty is depicted in Fig.3, where 
and the transfer function of the block within the broken line is , and this transfer function is
of course stable, resulting from designing a stable controller according to the condition in Theorem 1. Thus the loop gain transfer function is 
. It then follows the small-gain theorem that the combination of the controller and the actual plant will remain robustly stable
if .
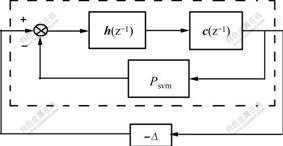
Fig.3 Simplified diagram of combination of controller and actual plant with uncertainty
Remark 2 From a practical point of view, Theorem 2 provides a method to judge whether the stability condition developed in Theorem 1 can ensure the stability of the actual closed-loop system, which can be illustrated as follows.
Although the actual plant is unknown, the discrepancy between SVM model and the actual plant can be measured through experiments. Suppose that a certain input u acts on the actual plant and SVM model respectively, and e denotes the output discrepancy. There exists 
from Eqn. (17). Now, assume a unit step-function input is applied, and then 
, i.e. 
. It holds true that 
≤
. From the difference between model output and plant output, 
can be easily obtained, and then the upper bound of is derived. For a SVMs-MPC closed-loop system, 
can be calculated. So from the constraint in Theorem 2, it can be determined whether the stability condition developed in Theorem 1 can guarantee that the actual closed loop is still stable.
5 Simulation results
Two examples were selected to demonstrate the results developed so far.
5.1 Example 1
An unknown linear plant is:
(19)
Obviously the plant itself is stable. Assume that the initial condition is x(0)=[0, 0]. SVM parameters are chosen as n=2, m=3, C=1×104 and ε=1×10-4. 200 pairs of samples are generated by applying random inputs uniformly distributed in the interval [-1,1].
The output responses are depicted in Fig.4 and the corresponding closed-loop poles are listed in Table 1, with different MPC parameters.
A unit step input is applied to the actual plant and SVM model respectively, and then we get 
. For the stable case Hp=Hu=Q=1, R=0.6, the robust stability constraint is 
. From time 60 to 500 due to system perturbation, the transfer function of the actual plant alters to be 
and 
respectively, where 
and 
, and then the output response is examined. As shown in Fig.5, the plant still remains stable under perturbation Δ2, whereas the plant becomes unstable under perturbation Δ1.
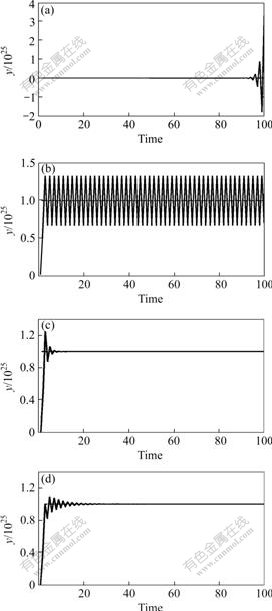
Fig.4 Output responses with different MPC parameters
(a) Hp=Hu=Q=1, R=0; (b) Hp=Hu=Q=1, R=0.5; (c) Hp=Hu=Q=1, R=1; (d) Hp=2, Hu=1, Q=diag{1,1}, R=0
Table 1 Closed-loop poles with different MPC parameters
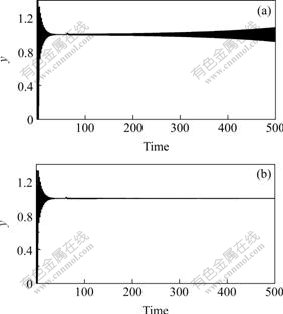
Fig.5 Output responses under perturbation
(a) 
; (b) 
5.2 Example 2
An unknown weakly nonlinear plant:
(20)
SVM parameters are n=2, m=3, C=1×104 and ε= 1×10-4. 200 pairs of samples are generated by applying random inputs uniformly distributed in the interval [-1,1].
A unit step input is applied to the actual plant and SVM model respectively, and then we get 
. MPC parameters are chosen as Hp=1, Hu=1, Q=1, R=0.001 and Hp=1, Hu=1, Q=1, R=1. The two closed loops are all stable. 
of the former is 0.8063 and that of the latter is 0.8633. So both cases can satisfy the robust constraint and the stability margin of the latter is larger than that of the former. From time 60 to 500, due to system perturbation, the transfer function of the
actual plant alters to be 
and 
respectively, where Δ1=0.78/z and Δ2=0.83/z. The output responses are depicted in Fig.6. And we can see that under perturbation Δ1 both closed loops still remain stable, but the control performance of the latter is better than that of the former, whereas under Δ2 the former becomes unstable and the latter is still stable. Fig.6 illustrates that the stability margin of the latter is larger than that of the former.
1) Finite horizon model predictive controller based on parallel SVMs may result in closed-loop unstable system.
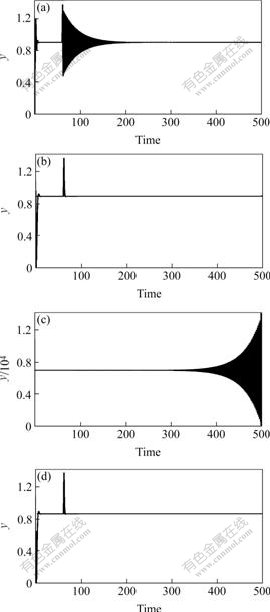
Fig.6 Output responses under perturbations
(a)
Δ1=0.78/z;
(b)
Δ1=0.78/z;
(c)
Δ2=0.83/z;
(d) Δ2=0. 38/z
2) Multi-step-ahead MPC strategy based on parallel SVMs with linear kernel was proposed, and then the necessary and sufficient stability condition of MPC closed loop according to SVM model was derived, and a method of judging the discrepancy between SVM model and the plant was presented.
3) The constraint sets for model/plant mismatch to ensure the real close-loop system are robustly stable. Simulation results show that the stability condition and the robust constraint sets can provide a convenient way to achieve parallel SVMs based MPC closed-loop system with larger stable margin.
References[1] MIAO Qi, WANG Shi-fu. Nonlinear model predictive control based on support vector regression[C]// Proceedings of the 1st International Conference on Machine Learning and Cybernetics. Beijing: 2002: 1657-1661.
[2] WANG Yu-hong, HUANG De-xian, GAO Dong-jie, et al. Nonlinear predictive control based on support vector machine[J]. Information and Control, 2004, 33(2): 133-136. (in Chinese)
[3] ZHANG Hao-ran, HAN Zheng-zhi, LI Chang-gang. Support vector machine based nonlinear model predictive control[J]. Systems Engineering and Electronics, 2003, 25(3): 330-334. (in Chinese)
[4] ZHONG Wei-min, PI Dao-ying. SVM with linear kernel function based nonparametric model identification and model algorithmic control[C]// IEEE Proceedings on Networking, Sensing and Control. Tucson: IEEE Press, 2005: 982-987.
[5] ZHONG Wei-min, HE Guo-long, PI Dao-ying et al. SVM with polynomial kernel function based nonlinear model one-step-ahead predictive control [J]. Chinese Journal of Chemical Engineering, 2005, 13(3): 373-379.
[6] ZHONG Wei-min, PI Dao-ying, SUN You-xian. Support vector machine based nonlinear model multi-step-ahead optimizing predictive control[J]. Journal of Central South University of Technology, 2005, 12(5): 591-595.
[7] LI Ping, LI Gang, MENG Ling-bai. Generalized predictive control for dual-control systems[J]. Journal of Central South University of Technology: Natural Science, 2003, 34(4): 386-389. (in Chinese)
[8] MACIEJOWSKI J M. Predictive Control with Constraints[M]. London: Prentice Hall, 2002.
[9] VAPNIK V N. The Nature of Statistical Learning Theory[M]. New York: Springer-Verlag, 1995.
[10] SMOLA A J, SCH?LKOPF B. A tutorial on support vector regression[R]. London: Royal Holloway College, London University, 1998.
[11] ZHU Jing. Intelligent Predictive Control and its Application[M]. Hangzhou : Zhejiang University Press, 2002. (in Chinese)
Foundation item: Project(2002CB312200) supported by the National Key Fundamental Research and Development Program of China; project(60574019) supported by the National Natural Science Foundation of China
Received date: 2006-12-20; Accepted date: 2007-03-23
Corresponding author: BAO Zhe-jing, Doctoral candidate; Tel: +86-571-87953761; E-mail: zjbao@iipc.zju.edu.cn
(Edited by YANG Hua)
