基于广义拉普拉斯分布的图像压缩感知重构

何宜宝，毕笃彦

(空军工程大学 航空航天工程学院，陕西 西安，710038)

摘 要：

知重构问题，构建图像小波系数的广义拉普拉斯统计模型。首先通过对典型图像小波系数的直方图统计，以广义拉普拉斯分布拟合图像小波系数的先验概率密度，用KL散度法求得广义拉普拉斯分布的参数。然后基于贝叶斯准则，通过取对数，将稀疏系数的最大后验概率估计问题转化为p范数优化问题，其中p的取值由待重构的图像所决定，即为该图像小波系数对应的广义拉普拉斯分布的形状参数。最后由非凸优化法求解得到图像的小波系数，并实现图像的重构。实验结果表明：对于简单稀疏信号，该方法重构成功率明显高于经典的BP和OMP法；对于测试图像的小波系数信号，所提方法能够自适应地精确重构原始图像。

关键词：

图像压缩感知; 先验分布; 广义拉普拉斯分布; 非凸优化；

中图分类号：TN911.73          文献标志码：A         文章编号：1672-7207(2013)08-3196-07

Image compressed sensing reconstruction based on Generalized Laplacian Distribution

HE Yibao, BI Duyan

(Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China)

Abstract: A probabilistic sparse model based on generalized Laplacian distribution is constructed to solve the popular problem of image compressed sensing. Through histogram statistics of wavelet coefficients of typical images, the generalized Laplacian distribution is chosen to fit prior distribution of the coefficients. Parameters of the distribution are estimated with a method of KL divergence. Based on Bayes’ rule, estimation of the maximum a posteriori of coefficients is transformed to a minimization problem of p norm, in which, the value of p is determined by shape parameter of the generalized Laplacian distribution corresponding to current image. Using nonconvex minimization, the coefficients are reconstructed. Experimental results show that, for simple sparse signal, exact reconstruct frequency of the proposed method is higher than BP and OMP; for the wavelet coefficients of test images, the proposed algorithm can reconstruct image exactly and adaptively.

Key words: image compressed sensing; prior distribution; generalized Laplacian distribution; nonconvex optimization

随着科技水平的发展，信号带宽越来越宽，数据采集尤其是图像采集中分辨率要求越来越高，伴随而来的是对宽带信号处理技术和海量传感器的需求不断增大，以及如何有效地压缩和存储海量数据。在此过程中，传统的香农抽样定理受到了挑战。原因在于传统数据采集方式存在较大的冗余，往往导致采集数据的泛滥和传感器的浪费。近年来，作为香农采样定理的另一种选择，压缩感知理论^[1-3]备受众多学者的关注。它通过对具有稀疏性或可压缩性的信号进行随机抽样，得到比香农采样定理条件下少得多的观测值，再利用信号在某种基下可稀疏表示，能以极大的概率从采样值中无失真重构原始信号，其中观测值数量取决于信号的稀疏度，而与信号的带宽无关。在压缩感知理论中，信号重构是其中重要的一部分，目前压缩感知重构算法主要有以下几种^[4]：(1) 贪婪算法^[5]。每一步迭代的过程中选择局部最优解，而最终得到全局最优解的一种逼近；(2) 凸优化法^[6]。将原问题以一个凸优化问题进行逼近，用解决凸优化的方法得到一个近似解；(3) 非凸优化法^[7]。即将原问题以一个非凸优化问题进行逼近；(4)贝叶斯法^[8-9]。根据稀疏度估计所求系数的先验分布，然后由观测值进行最大后验概率估计，求得系数可能分布的概率最大的一个区域。其他的方法还有利用小波系数稀疏结构的模型化压缩感知^[10-12]和基于图模型的信息传播技术^[13-14]等。其中贪婪算法和凸优化法是目前较为成熟的方法，具有较充分的理论支撑，分别具有计算速度快和鲁棒性强的优点，其他方法虽然提供了一些新的求解思路，然而都缺乏足够的理论保证。因此，贪婪算法和凸优化法是使用频率较高且具有代表性的2种方法。在贝叶斯法中，描述信号系数稀疏性的先验分布的选择是非常重要的，以往文献中有利用分层先验(hierarchical prior)描述方法对信号的小波系数进行描述，而没有选用具有稀疏描述性能的拉普拉斯分布(laplace prior)，原因在于拉普拉斯分布与高斯似然函数不共轭，即由两者得到的后验分布不属于拉普拉斯分布族。针对此问题，文献[9]利用层级形式的拉普拉斯先验分布对信号的稀疏性进行建模，并在此基础上进行了快速算法的设计。然而，对于图像信号的重构，上述2种方法所选择的先验分布并不适用，原因在于图像信号的小波系数并非真正意义的稀疏信号，而是可压缩信号^[12]，相对于稀疏信号，其更加“稠密”，上述方法已不能精确地描述图像小波系数的分布；同时，对于不同的图像，其系数分布的概率密度函数也有所不同，需要根据待重构图像的不同，选择不同的先验分布。因此，本文作者针对图像信号的压缩感知重构问题，提出了一种基于广义拉普拉斯分布的图像重构方法。该方法的思想是，首先利用图像小波系数的先验统计模型，估计得到具有稀疏描述性能的广义拉普拉斯分布，即图像小波系数的先验分布；然后基于贝叶斯准则，求系数的最大后验概率估计，在求解过程中，该问题转化为一个非凸优化问题；最后由小波反变换重构图像。其中图像小波系数的先验统计模型分2种，基于各子带的统计模型和基于所有高频系数的模型。

1  压缩感知理论

设N×N的矩阵Ψ为小波基矩阵，对于大多数自然信号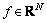，可以用小波基Ψ进行稀疏表示，即f=Ψs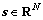，为小波系数矢量，其中大部分系数的幅度值趋于0。基于压缩感知理论，这些稀疏信号或可压缩信号，可通过观测矩阵Φ(M×N)直接获得一个观测值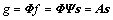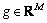，，其中M＜＜N，A为感知矩阵。由该观测值和矩阵A，通过求解下列最优化问题，可得系数矢量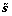，然后再对其进行小波反变换即可重构出原信号f。

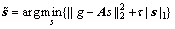        (1)

该方法即为典型的凸优化方法，通过线性规划或贪婪迭代最终能够得到单一的精确解。

与上述方法不同，贝叶斯法将所有的未知量以满足一定概率分布的随机量进行描述。假定观测过程中含有噪声n，即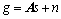，则该噪声可以用零均值的高斯噪声进行逼近，未知方差设为σ²，那么对上述观测过程进行高斯似然建模，可得下式：

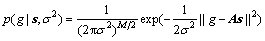  (2)

如果事先设定s满足某种稀疏先验分布，则压缩感知信号重构过程即转化为求s的后验概率密度。

在求解过程中，除了求得更精确的s，更重要的是，这种贝叶斯方法提供了一种新的架构，用于研究之前没有涉及的问题，即，不是求得对s的单点估计，而是其后验分布，并得到估计f的误差棒(error bars)和重构信号的不确定性估计，这种不确定性估计可以为自适应测量的设计提供依据^[8]。

2  基于广义拉普拉斯分布的压缩感知图像重构

在贝叶斯压缩感知架构中，对稀疏系数的先验描述是否准确关系到重构得到的信号是否精确。近年来，该研究的重点是如何准确地描述图像分布的非高斯性和小波系数的稀疏性^[8-9]。图像分布的非高斯性主要体现在：大部分区域都是光滑的，只有很少一部分区域是轮廓和边缘。将这种图像映射到小波域则表现为稀疏特性分布。这种稀疏性在小波系数的概率密度函数中表现出尖峰与“重拖尾”(heavy tails)的特点，该特点说明了小波系数以较大的概率趋近于零值，偶尔有少部分的系数较大。对于具有这种特点的概率密度函数的描述，广义拉普拉斯分布(Generalized Laplacian Distribution, GLD)是其中重要的一种。Mallat^[15]首先中用广义拉普拉斯分布对小波系数的统计特性进行了描述；文献[16]基于广义拉普拉斯分布，构建了描述小波系数的统计模型，并用于图像压缩中；文献[17]则将其归于具有稀疏描述性能的概率密度函数集中。因此，本文用广义拉普拉斯分布来描述图像小波系数的先验概率密度。

2.1  基于广义拉普拉斯分布的小波系数统计模型

广义拉普拉斯分布又称为广义高斯分布或扩展的指数分布(stretched exponential distribution)，其概率密度函数表示如下：

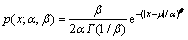        (3)

其中：μ为均值；α，β分别为刻度参数和形状参数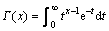；，即伽玛函数。本文采用均值为0，即μ=0的广义拉普拉斯分布描述小波系数的统计分布。不同形状参数的零均值广义拉普拉斯分布概率密度函数如图1所示(α=1)。当形状控制参数β=2时，该分布变成高斯分布；当β=1时，该分布变成拉普拉斯分布。形状参数越小，概率密度函数变化越陡。

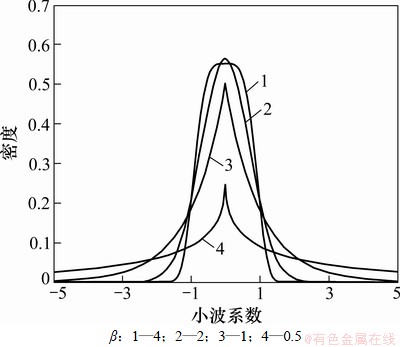
图1  不同形状参数的零均值广义拉普拉斯分布概率密度函数

Fig. 1  Probability density function of generalized Laplacian distribution with different shape parameters

参数α，β与二阶矩和四阶矩的关系如下式：

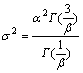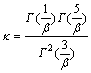，        (4)

式中：σ²为方差；κ为峰度。

对于参数α和β的求解，本文采用最小化相对熵(relative entropy)或称作KL散度(Kullback-Leibler divergence)法。基本思想是通过求解拟合的离散分布与系数直方图的相对熵来描述得到的概率密度函数的精确度，如下式所示：

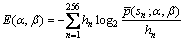        (5)

其中：h_n为小波系数落在第n个直方图区间的概率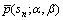；为式(3)在第n个直方图区间内的积分；c_n为该区间的中值。

在小波系数统计模型拟合过程中，考虑2种方法，第1种为对所有的高频系数进行直方图统计，第2种为分别对小波系数中垂直、水平和对角子带进行直方图统计，最后由重构结果对比这2种方法的优劣。

(1) 关于所有高频系数的统计模型

对图像Lena等进行1层Har小波变换后的所有高频系数进行直方图统计，区间分级为256，对概率密度取对数后，结果如图2实线所示。同时，由最小化相对熵法，针对不同的图像，估计其广义拉普拉斯分布的参数α，β，并计算最小的相对熵值，最后得到的各自图像的广义拉普拉斯分布如图2中虚线所示，并给出了各自的形状参数和最小相对熵值。

由图2可以看出：对于不同的图像类型，选择合适的形状参数后，广义拉普拉斯分布可以很好地拟合其小波系数的概率密度函数。其中Fingerprint图像是所选的几幅图像中最具高斯性的，而其拟合的效果也最差。其他的图像较好地表征了小波系数分布的非高斯性和稀疏性。

(2) 关于各子带系数的统计模型

同样，对所选图像先进行1层Har小波变换，然后对垂直、水平和对角子带系数分别进行直方图统计，区间仍划分256级，对Man和Hill图像统计结果如图2中的实线所示。由最小相对熵法拟合的广义拉普拉斯分布如图中虚线所示，并分别计算出了对应的形状参数和最小相对熵。

由图3的结果与(a)中统计模型的结果对比可知，针对同一图像，基于各子带系数拟合的统计模型误差普遍较基于所有系数拟合的误差要大，并且由各子带系数拟合的拉普拉斯分布的形状参数也各不相同，说明各子带系数具有不同的稀疏度，特别是对角子带与其他2个子带有比较明显的差异。

2.2  基于贝叶斯准则的系数求解

通过对图像的小波系数进行统计建模和广义拉普拉斯分布拟合后，得到了其先验概率密度函数p(s)。可利用贝叶斯准则，对系数s进行最大后验概率估计计算如下：

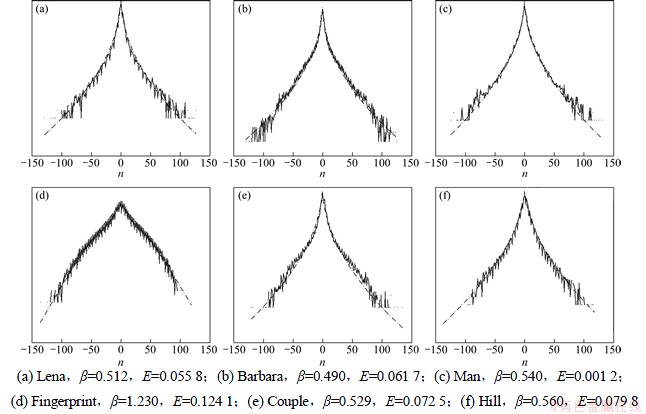
图2  256-bin小波系数统计直方图(对数域)(其中虚线为拟合的广义拉普拉斯分布，下方为对应的形状参数和最小相对熵)

Fig. 2  Example of 256-bin coefficient histograms (solid lines) fitted with density of Equation (3) (dotted lines),plotted in log domain

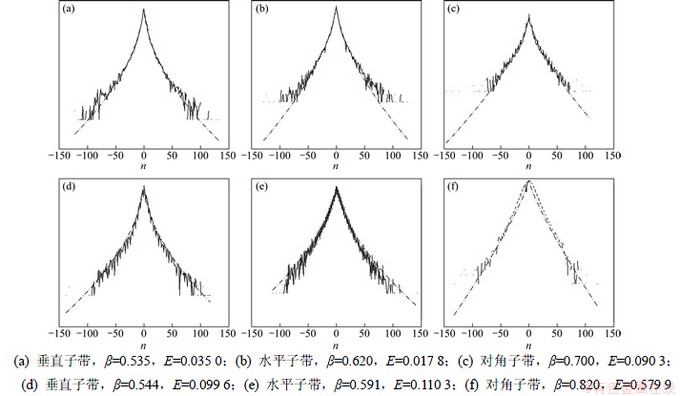
图3  基于各子带的256-bin小波系数统计直方图(对数域)(其中虚线为拟合的广义拉普拉斯分布)

Fig. 3  Example of 256-bin subband coefficient histograms (solid lines) fitted with density of Equation (3) (dotted lines),plotted in log domain

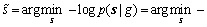
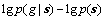           (6)

其中p(g|s)，p(s)均为已知，则式(6)可化简为：

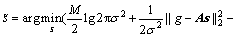
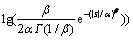          (7)

去掉与系数s无关项后化为：

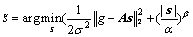      (8)

从形式上来看，式(8)与典型的最优化问题(1)类似，但实质却有很大的不同。式(1)中的L1范数针对不同分布的解，是固定的；而式(8)中的参数α和β取决于不同图像的小波系数分布情况，对于具有不同特征的图像，如Lena和Fingerprint，最后得到的优化问题有较大的区别，Lena图像对应的优化问题中β＜1，而Fingerprint图像对应的优化问题中β＞1。另外，如果选择统计模型(b)，各子带系数分布情况不同而使得各自对应的优化问题也不相同，因此，式(8)的优化问题更具有自适应性，对于不同的图像，可以是一个凸优化问题，也可以是非凸优化问题。不过，从上文中选择的几幅图像来看，多数图像的小波系数分布对应的广义拉普拉斯分布的形状参数β＜1，只有Fingerprint例外，因此需要求解的优化问题多为非凸优化问题。

2.3  p范数优化问题求解

首先要说明的是，本文通过对p范数优化问题的求解主要用来说明上述所建统计模型在压缩感知图像重构中的有效性，因此在这里主要使用已有的p范数优化法，并且主要针对p＜1的情况。对于p＜1的p范数优化问题，文献[18]对此进行了研究，并与p=1即L1范数优化法作了详细的对比。文献[18]将p范数优化问题进行加权L2范数代换：

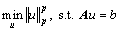             (9)

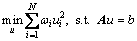           (10)

其中，权值ω_i由前一次计算结果u^(n-1)求得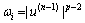，。式(10)通过求解Euler-Lagrange方程可得

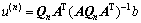          (11)

Q_n为一对角阵，元素为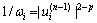。然而当p＜1时，p-2为负，则u^(n-1)=0时，ω_i将不存在。为解决这一问题，文献[19]对ω_i的计算方法修正如下：

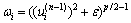           (12)

其中：ε＞0。同时，给出了ε的调整策略，即先赋以较大的值，然后算法收敛后再逐步减小。实验证明，调整后的方法有效地提高了信号的重构性能，因此，本文使用文献[19]的求解方法。

3  实验结果及分析

为证明本文方法的正确性和有效性，在MatlabR2008a中分别对构造的稀疏信号和图像的小波系数信号进行压缩感知信号重构实验。首先，针对稀疏度不同的信号而观测次数相同和稀疏度相同的信号而观测次数不同2种情况，分别采用BP，OMP和p范数优化法进行重构，其中p范数优化法中，p取值为[0,1]，通过计算重构成功率对比它们的重构性能；然后，针对不同图像的小波系数信号，依据上述2种模型，采用BP，OMP和p范数优化法进行重构，并进行了性能对比。

3.1  简单稀疏信号重构性能的比较

对于不同稀疏度的0-1随机信号，设信号长度N=512，测量次数M=128，采用高斯随机测量矩阵，改变稀疏度，进行500次的模拟实验，成功重构的标准设为均方误差小于10^-6，结果如图4所示。其中BP 和OMP算法的实现均来自SparseLab工具包^[20]，BP法中PDCO(Primal-Dual Barrier Method for ConvexObjectives)最大迭代次数设为50，误差容限为10^-8；OMP最大迭代次数为500，误差容限为10^-5。

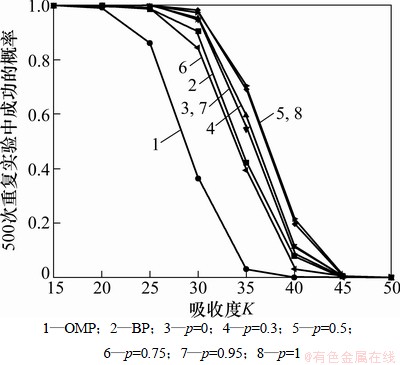
图4  N=512，M=128时，不同信号的稀疏度下BP，OMP和本文方法重建结果的比较

Fig. 4  Performance comparison of BP, OMP and proposed method with N=512, M=128

对于稀疏度相同的信号，设信号长度N=512，稀疏度K=40，改变观测数，进行500次的模拟实验，结果如图5所示。

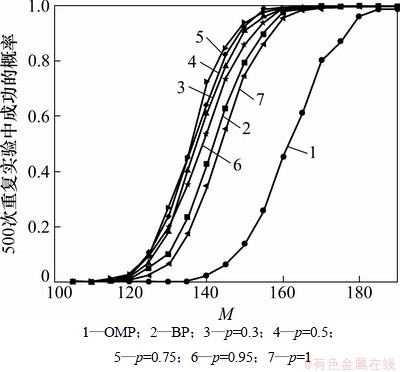
图5  N=512，K=40，不同测量次数下BP，OMP和本文方法重建结果的比较

Fig. 5  Performance comparison of BP, OMP and proposed method with N=512, K=40

从图4可看出：测量次数一定，随着信号稀疏度的增加，信号重建成功的概率逐渐减小，在信号非常稀疏的情况下，均高概率精确重建原始信号，但OMP成功概率最低，而p范数优化法则以相对较高概率精确重建原始信号，其中p取不同的值，其重建性能有所不同，p=0.5和p=0.75性能接近，但随着p的减小或增加，其重构性能均下降。从图5可见：稀疏度一定，随着测量次数增多，信号重建的概率逐渐增大，相比较而言，p范数优化法精确恢复原始信号所需测量次数最少，其中p=0.5和p=0.75重构性能较好并且非常接近，同样随着p的减小或增加，其成功重构信号的概率下降。

3.2  针对图像小波系数信号的重构

由图像小波系数拟合得到的广义拉普拉斯分布可知，对于大部分图像(类似于Fingerprint的图像，本文暂不考虑)，其广义拉普拉斯分布的形状参数范围为[0.5，0.8]^[12]，结合上述实验分析，p范数优化法中p的取值恰好在此范围内时，其性能较优越。因此，基于上述建立的广义拉普拉斯分布模型，先得到待重构图像系数分布的形状参数，然后由此参数得到适合该图像的重构方程(8)，最终由p范数优化法进行求解。

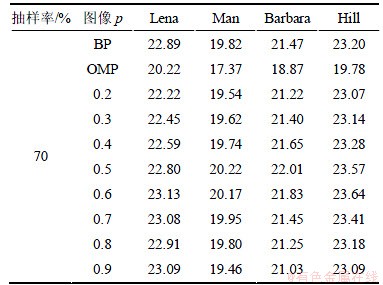
选取512×512的Lena，Man，Barbara，Hill等测试图像，如果直接对这些图像进行压缩采样，则其需要的存储量和计算量相当庞大，因此参考文献[12]中对测试图像的处理方法，在行列方向上每隔8点进行抽样，形成64×64的小尺寸图像，小波基为“db4”小波，进行一层小波变换，针对该信号，构造高斯随机测量矩阵分别对其进行压缩采样，然后分别利用BP，OMP以及p范数优化法进行重构，抽样率为70%时的重构峰值信噪比如表1所示。从表1可以看出：OMP法的重构效果最差，低于BP法重构结果2~3 dB。在p取值为[0.5，0.8]范围内时，p范数优化法得到的重构结果最优，并优于BP和OMP法。因此，首先基于广义拉普拉斯分布统计模型确定形状参数，然后依据此参数求解对应的p范数优化问题，可以依据图像自身的特征自适应的对其进行压缩感知重构，有效地提高了重构性能。

表1  基于广义拉普拉斯模型重构与BP和OMP重构的PSNR比较

Table 1  PSNR comparison of reconstructed image using BP,OMP and proposed method          dB

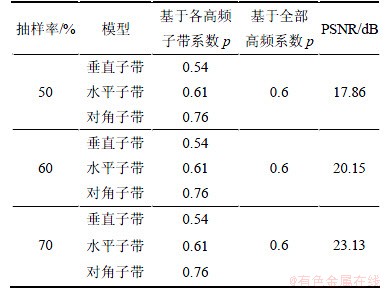
为了对比模型(a)和(b)，在此以Lena图像为例，采用2种方式进行重构，第1种为基于p范数优化法分别重构各高频子带系数后重构图像，针对不同的子带p取不同的值，通过对Lena图像的直方图统计，其垂直、水平和对角子带系数对应的广义拉普拉斯分布的形状参数分别为0.54，0.61和0.76，因此在p范数问题求解中，p取相应的值；第2种为基于p范数优化法重构全部高频系数后重构图像，其中p=0.6。抽样率为50%，60%，70%条件下，基于2种模型的重构结果对比见表2。

由表2可知：基于各子带系数的统计模型分别进行重构得到的结果明显逊于基于全部高频系数的重构结果。其原因在于，在2种统计模型中，基于各高频子带拟合得到的广义拉普拉斯分布与各子带系数直方图之间的最小相对熵要明显大于基于全部高频系数模型的最小相对熵，当分别对各子带系数进行重构后再重构图像时，容易出现误差积累，导致最终图像重构结果不理想。

表2  基于不同统计模型的Lena图像重构结果对比

Table 2  Reconstruction results of Lena using different statistical model

4  结论

(1) 基于典型图像的小波系数直方图统计，构造了2种统计模型，以广义拉普拉斯分布作为图像小波系数的先验概率密度描述，并通过KL散度法求得分布的各参数。然后由贝叶斯准则，将图像系数的最大后验概率估计转化为非凸优化问题。

(2) 通过对简单稀疏信号和标准测试图像的重构实验表明，所提方法重构性能要优于典型的BP和OMP法，同时针对不同的图像，具有较好的适应性。

(3) 对比2种统计模型的重构结果，基于各高频子带系数模型的重构性能较基于全部高频系数模型的低。

参考文献：

[1] E, Romberg J, Tao T. Stable signal recovery from incomplete and inaccurate information[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207-1233.

[2] E, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction form highly incomplete frequency information[J]. IEEE Trans Information Theory, 2006, 52(2): 489-509.

[3] Donoho D L. Compressed sensing[J]. IEEE Trans Information Theory, 2006, 52(4): 1289-1306.

[4] Tropp J, Wright S. Computational methods for sparse solution of linear inverse problems[J]. Proc of the IEEE, 2010, 98(6): 948-958.

[5] Mallat S, Zhang Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Trans Signal Processing, 1993, 41(12): 3397-3415.

[6] Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM Rev, 2001, 43(1): 129-159.

[7] Chartrand R. Exact reconstruction of sparse signals via nonconvex minimization[J]. IEEE Signal Processing Letter, 2007, 14(10): 707-710.

[8] Ji S, Xue Y, Carin L. Bayesian compressive sensing[J]. IEEE Trans Signal Processing, 2008, 56(6): 2346-2356.

[9] Babacan S D, Molina R, Katsaggelos A K. Bayesian compressive sensing using laplace priors[J]. IEEE Trans on Image Processing, 2010, 19(1): 53-63.

[10] 练秋生, 王艳. 基于双树小波通用隐马尔科夫树模型的图像压缩感知[J]. 电子与信息学报, 2010, 32(10): 2301-2306.

LIAN Qiusheng, WANG Yan. Image compressed sensing based on universal HMT of the Dual-tree wavelets[J]. Journal of Electronics & Information Technology, 2010, 32(10): 2301-2306.

[11] 练秋生, 肖莹. 基于小波树结构和迭代收缩的图像压缩感知算法研究[J]. 电子与信息学报, 2011, 33(4): 967-971.

LIAN Qiusheng, XIAO Ying. Image compressed sensing algorithm based on wavelet tree structure and iterative shringkage[J]. Journal of Electronics & Information Technology, 2011, 33(4): 967-971.

[12] Baraniuk R G, Cevher V, Marco T D, et al. Model-based compressive sensing[J]. IEEE Trans. Information Theory, 2010, 56(4): 1982-2001.

[13] Baron D, Sarvotham S, Baraniuk R G. Bayesian compressive sensing via belief propagation[J]. IEEE Trans Signal Processing, 2010, 58(1): 269-280.

[14] Donoho D L, Maliki A, Montanari A. Message-passing algorithms for compressed sensing[J]. Proc Natl Acad Sci, 2009, 106(45): 18914-18919.

[15] Mallat S G. A theory for multiresolution signal decomposition: The wavelet representation[J]. IEEE Trans PAMI, 1989, 11(7): 674-693.

[16] Buccigrossi R W, Simoncelli E P. Image compression via joint statistical characterization in the wavelet domain[J]. IEEE Trans Image Processing, 1999, 8(12): 1688-1701.

[17] Cevher V. Learning with compressible priors[J]. Neural Information Processing Systems (NIPS), 2008, 12: 7-12.

[18] Rao B D, Kreutz-Delgado K. An affine scaling methodology for best basis selection[J]. IEEE Trans Signal Processing, 1999, 47(1): 187-200.

[19] Chartrand R, Yin W. Iteratively reweighted algorithms for compressive sensing[C]//Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing. Las Vegas, NV: IEEE, 2008: 3869-3872.

[20] Donoho D L, Stodden V, Tsaig Y, et al. SparseLab [EB/OL]. [2012-02-10]. http: //sparselab.stanford.edu

(编辑  陈爱华)

收稿日期：2012-09-16；修回日期：2012-12-11

基金项目：国家自然科学基金资助项目(61175029)；国防科技重点实验室基金资助项目(9140c610301080c6106，9140c6001070801)；航空科学基金资助项目(20115896022)

通信作者：何宜宝(1985-)，男，河南宜阳人，博士研究生，从事压缩感知信号重构研究；电话：13629240714；E-mail：gudujianboboo@yahoo.com.cn

摘要：针对图像压缩感知重构问题，构建图像小波系数的广义拉普拉斯统计模型。首先通过对典型图像小波系数的直方图统计，以广义拉普拉斯分布拟合图像小波系数的先验概率密度，用KL散度法求得广义拉普拉斯分布的参数。然后基于贝叶斯准则，通过取对数，将稀疏系数的最大后验概率估计问题转化为p范数优化问题，其中p的取值由待重构的图像所决定，即为该图像小波系数对应的广义拉普拉斯分布的形状参数。最后由非凸优化法求解得到图像的小波系数，并实现图像的重构。实验结果表明：对于简单稀疏信号，该方法重构成功率明显高于经典的BP和OMP法；对于测试图像的小波系数信号，所提方法能够自适应地精确重构原始图像。