J. Cent. South Univ. (2017) 24: 1174-1182
DOI: 10.1007/s11771-017-3520-y
Lattice Boltzmann method for thermomagnetic convection of paramagnetic fluid in square cavity under a magnetic quadrupole field
XIE Nan(谢楠), JIANG Chang-wei(姜昌伟), HE Yi-hai(何贻海), YAO Ming(姚鸣)
Key Laboratory of Efficient and Clean Energy Utilization of College of Hunan Province, School of
Energy and Power Engineering, Changsha University of Science and Technology, Changsha 410114, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract:
Numerical study was performed for a better understanding on thermomagnetic convection under magnetic quadrupole field utilizing the lattice Boltzmann method. Present problem was examined under non-gravitational and gravitational conditions for a wide range of magnetic force number from 0 to 1000. Vertical walls of the square cavity were heated differentially while the horizontal walls were assumed to be adiabatic. Distributions of the flow and temperature field were clearly illustrated. Under non-gravitational condition, the flow presents a two-cellular structure with horizontal symmetry, and the average Nusselt number increases with the augment of magnetic force number. Under gravitational condition, two-cellular structure only occurs when the magnetic field is relatively strong, and the average Nusselt number decreases at first and then rises with the enhancing magnetic field. Results show that the magnetic field intensity and the Rayleigh number both have significant influence on convective heat transfer, and the gravity plays a positive role in heat transfer under weak magnetic field while a negative one for magnetic force numbers larger than 1×105.
Key words:
lattice Boltzmann method; thermomagnetic convection; magnetic quadrupole field; magnetic force;
1 Introduction
Natural convection in the presence of magnetic field has become a research focus in recent decades because it has a wide range of engineering applications like crystal and protein growth, nuclear technology, embarked electronics, etc. It has already been noticed that the magnetic field has significant effect on the convective heat transfer and the influence is different for various configurations of the applied magnetic field. GHASEMI et al [1] numerically studied the natural convection under a horizontal magnetic field and found that the heat transfer rate increases with the augment of Rayleigh number while decreases with the increasing Hartmann number. The same conclusion was proved by AL-ZAMILY [2] and the magnetic field applied in this work was in the vertical direction. The effect of an axial magnetic field and a radial magnetic field on the natural convection was examined by SANKAR et al [3, 4] and KUO and LEONG [5]. Their results revealed that in shallow cavities, the axial magnetic field is more effective in suppressing the flow and heat transfer of natural convection, while the radial magnetic field is more efficient in deep cavities. It was proved by many researchers that the inclination angle of magnetic field also has a remarkable effect on the heat transfer for various convective conditions [6-9], which makes the inclination angle a significant factor. ASHOURI et al [10] numerically investigated the convective heat transfer in a cavity induced by magnetic field gradient generated by a strip permanent magnet. They pointed out that the convective heat transfer increases with the strengthening of magnetic field.
Traditional CFD methods like finite volume method, finite difference method and finite element method are commonly-used methods for solving the various convective problems [1-10], while the lattice Boltzmann method has already become an available numerical method [11, 12]. LBM is a programming easily numerical method with simple algorithms and also has capabilities of solving the simulation of microflows, nanopaticles, crystal growth, porous media and many other complex convective heat transfer problems. MOHAMAD and KUZMIN [13] tested three common schemes for implementing the source term into LBM to prove the reliability of this numerical method. LI et al [14] utilized pure FVM, pure LBM and the coupled method to solve the natural convection with different Rayleigh numbers and agreed results were obtained.Natural convection under horizontal magnetic field was numerically studied using LBM by many other authors [15-21]. KEFAYATI et al [22] numerically simulated the MHD mixed convection in a lid-driven square cavity under horizontal and vertical magnetic field and totally different distributions of the streamlines and isotherms were observed. Their results showed that the direction of the magnetic field affects the heat transfer to a large extent. XUAN et al [23] designed a micro channel with a ferrofluid flowing through, and they obtained the temperature distributions and flow characteristics by changing the magnitude and orientation of the magnetic gradient to analyze its flow and thermal processes. HUSSEIN et al [24] numerically investigated the MHD natural convection in an open enclosure using LBM, and they found that the flow circulation intensity and the convection effect start to decrease when increasing the orientation angle of magnetic field. MAHMOUDI et al [25] also used LBM to examine the case in a cavity with bottom wall being heated uniformly and vertical walls being heated linearly, and they found that the direction of the magnetic field controls the effect of nanoparticles. Point magnetic pole was also employed to analyze the thermomagnetic convection in square cavity by using LBM [26, 27].
Recently, the booming development of superconducting magnets provokes the relevant researches on thermomagnetic convection of non- conducting fluids like paramagnetic fluids (air, protein, glycerol aqueous solution) and diamagnetic fluids (water, hydrogen). YANG et al [28, 29] investigated the thermomagnetic convection of air in an inhomogeneous magnetic field generated by four permanent magnets. Their results indicated that different flow and heat transfer characteristics were caused by the centrifugal magnetic force. Lattice Boltzmann method has also been proved by many researchers as a valuable and powerful tool in dealing with air natural convection and heat transfer problems, even in complex geometries [30-32]. Thus, it is of great necessity to study the natural convection of air under magnetic quadrupole field, also to extend the application of LBM on thermomagnetic convection of paramagnetic fluid. In this work, standard D2Q9 model and temperature-density double distribution equations of LBM are employed to study the present problem. Effects of the magnetic quadrupole field are compared under non-gravitational and gravitational conditions.
2 Problem statement
Geometry of the present problem and the coordinate system are described in Fig. 1. The system consists of a two-dimensional square cavity which is horizontally placed and four permanent magnets which generate a steady inhomogeneous magnetic field. Vertical walls of this cavity are heated differentially, temperature of the left wall is maintained at Th while the temperature of the right is fixed at Tc, and Th is hotter than Tc. The other walls are assumed to be insulated. Cartesian coordinates are utilized and the origins of coordinates are fixed at the left bottom corner of the enclosure. The gravitational force acts in the minus y direction. In the present study, the length of the enclosure L, the length of the permanent magnets L1, and the distance between two opposite permanent magnets L2 are 0.024 m, 0.02 m, 0.03 m, respectively.
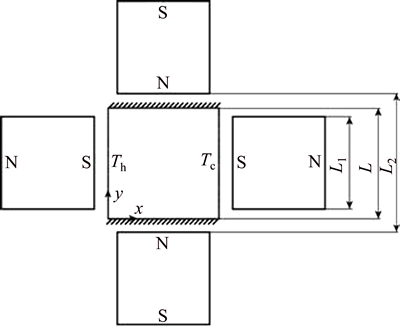
Fig. 1 Physical model and Cartesian coordinates
3 Mathematical formulation
3.1 Governing equations
The fluid is assumed to be Newtonian and incompressible. The flow in this enclosure is steady, and the viscous heat dissipation and magnetic dissipation are neglected. According to TAGAWA et al [33], Navier Stokes equation with external magnetizing force term can be described as
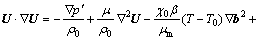
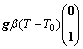 (1)
(1)
where U is the velocity vector; p=p0+p'; p' is the pressure difference due to the perturbed state, Pa; ρ0 is the fluid density at reference temperature, kg·m-3; μ is the fluid dynamic viscosity, kg·m-1·s-1; χ0 is the mass magnetic susceptibility at reference temperature, m3·kg-1; μm is the magnetic permeability, H·m-1; T is the fluid temperature and T0=(Th+Tc)/2, K; subscripts 0, h, c represent the reference value, hot and cold, respectively; b is the magnetic flux density, T; g is the gravitational acceleration, m·s-2; β is the thermal expansion coefficient, K-1.
For simplicity, subscripts of physical parameters and the superscript of pressure are omitted. Thus, the two-dimensional governing equations with body forces can be described as follows.
Continuity equation:
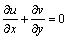 (2)
(2)
Momentum equations:
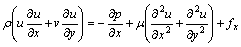 (3)
(3)
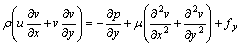 (4)
(4)
Energy equation:
 (5)
(5)
The body forces are defined as follows:
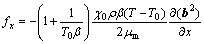 (6)
(6)
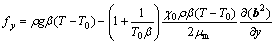 (7)
(7)
where x and y-coordinates are along with the horizontal and vertical direction, respectively; u and v are the velocity components in x-direction and y-direction, m·s-1; α is the thermal diffusivity.
In order to describe the characteristics of the present problem more clearly, the following dimensionless parameters are used to transform Eqs. (2)-(5) into dimensionless form:
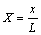 ,
, 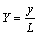 ,
, 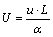 ,
, 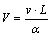 ,
,
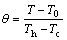 ,
, 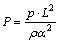 ,
, 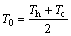 ,
,
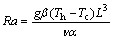 ,
, 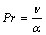 ,
, 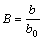 ,
,
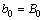 ,
, 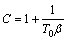 ,
, 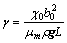 (8)
(8)
where X and Y are the dimensionless coordinates; U and V are the dimensionless velocity components; θ is the dimensionless temperature; P is the dimensionless pressure; Pr is the Prandtl number; b0 is the reference magnetic flux density, T; Ra is the Rayleigh number; γ is the dimensionless magnetic flux density. Governing equations in dimensionless form are given as follows:
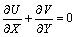 (9)
(9)
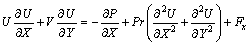 (10)
(10)
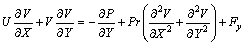 (11)
(11)
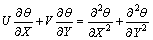 (12)
(12)
The dimensionless body forces are defined as follows:
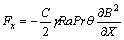 (13)
(13)
 (14)
(14)
3.2 Lattice Boltzmann equations
In the present research, standard D2Q9 model of LBM is employed for flow and temperature. The velocity vectors of present problem are illustrated in Fig. 2. The discrete velocity set for the D2Q9 model is
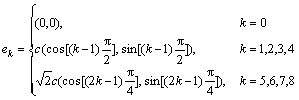 (15)
(15)
where ek are the discrete velocities of the lattice. The weighted factors of the lattice ωk are assigned as: ω0=0, ω1-4=1/9, ω5-8=1/36. The lattice Boltzmann equation with external forces can be written as follows.
The flow field:
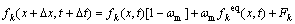 (16)
(16)
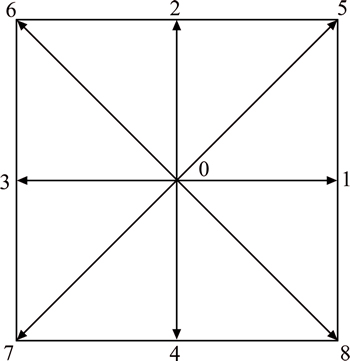
Fig. 2 Nine directions in D2Q9 model
The temperature field:
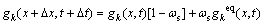 (17)
(17)
where f is the density distribution functions, and g is the internal energy distribution function. The external force term Fk, factors ωm and ωs are defined as follows:
 (18)
(18)
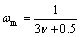 (19)
(19)
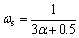 (20)
(20)
And the equilibrium density distribution functions f eq and the equilibrium internal energy distribution functions geq can be defined as
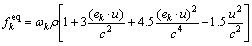 (21)
(21)
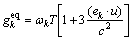 (22)
(22)
3.3 Boundary conditions
Bounce-back boundary conditions are utilized on all the walls of the closed square cavity, so the following conditions are imposed on the density distribution functions of the solid boundaries. For instance, boundary conditions for the top wall as well as the left wall are
Top wall: 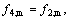
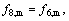
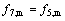 (23)
(23)
Left wall: 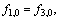
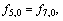
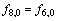 (24)
(24)
where 0 and m are the lattice on the boundary.
Vertical walls are heated differentially while the horizontal walls are adiabatic. Following conditions are imposed on the internal distribution functions. Use the vertical boundary conditions as examples:
Left wall: 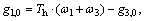
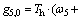
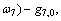
 (25)
(25)
Right wall: 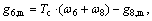
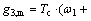
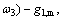
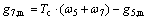 (26)
(26)
The average Nusselt number on hot wall is used to describe the heat transfer properties:
 (27)
(27)
4 Code validation and grid independence
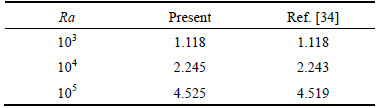
Different grid sizes of 50×50, 100×100 and 250×250 were tested and compared to ensure the grid independence. The 100×100 lattice node was selected in this work for the computations in a FORTRAN code. In order to testify the validity and correctness of the code and the grid in the present work, a range of numerical simulations were carried out using LBM under the similar conditions in published literature by DAVIS [34] and appropriate agreements were obtained as listed in Table 1.
Table 1 Comparison of present results with previous work for different Rayleigh numbers when Pr=0.7
5 Results and discussion
5.1 Results under non-gravitational condition
The Rayleigh number equals zero and γ turns out to be infinite under non-gravitational condition, so the parameter γRa is currently utilized to analyze the effect of magnetic field. Contours of stream function and isotherms are obtained with γRa varying from 1×104 to 1×107, and the most typical cases are shown in Fig. 3. Pure thermomagnetic convection is spotted in the cavity because the magnetic buoyancy force is the only factor that affects the heat transfer. When γRa is small as 1×104,an anticlockwise vortex in the upper part of the cavity and a clockwise vortex in the lower part can be observed. These two vortexes are symmetrical about the horizontal middle line of the enclosure, which suggests that the centrifugal buoyancy force drives the air along with the middle line from the hot wall to the cold wall. It is because the magnetic susceptibility of paramagnetic fluid is in the inverse proportional relationship to the fluid temperature. Thus, the cold fluid has a larger magnetic susceptibility than the fluid with a higher temperature, so the flow from the left separates near the cold wall and then goes back to the left along the top and bottom walls. The rotation is weak and the change of isotherms is insignificant, which declares an inefficient heat transfer performance. With the increasing value of γRa, the effect of magnetic field is much more remarkable and velocities of the flow grow faster and the vortexes start to expand. It can be distinctly observed that the isotherms travel more forward with the augment of the magnetic field. Obvious temperature gradients are spotted on the upper and lower side of the hot wall and the middle of cold wall, so the heat transfer is greatly enhanced. When γRa is equal to or greater than 5×105, the flow is intense and a significant thermal plume towards the cold wall can be noted.
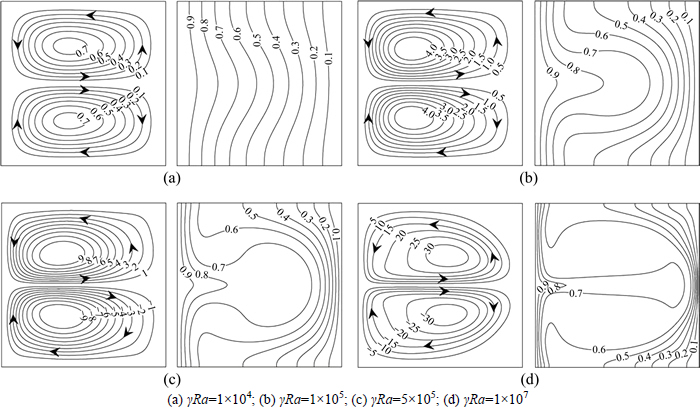
Fig. 3 Effect of γRa on streamlines and isotherms:
Figure 4 illustrates the effect of γRa on the local Nusselt number of left vertical wall under non-gravitational conditions. It is found that the local Nusselt number on hot wall increases with the augment of γRa, and the variation curves are horizontally symmetric. Maximums exist at the upper and lower position of the hot wall and the only minimum locates at the midpoint. The curves of local Nusselt number on cold wall are depicted in Fig. 5 where the local Nusselt number is also an increasing function of γRa. The only difference is that there is only one extreme value on these curves.
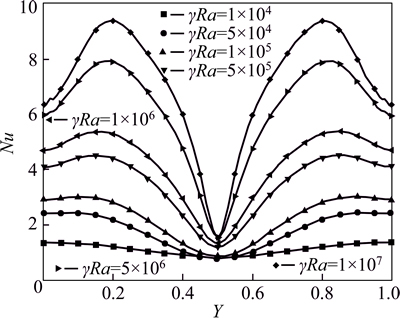
Fig. 4 Effect of γRa on local Nusselt number of left wall under non-gravitational conditions
5.2 Results under gravitational condition
Streamlines and isotherms under the combined effect of gravitational buoyancy force and magnetic buoyancy force are depicted in Fig. 6. Magnetic force number γ is currently used to describe the magnetic field intensity. The magnetic buoyancy force is insignificant when the γ is 1 or less, so the buoyancy due to density difference is dominant. Although the cold fluid has a larger magnetic susceptibility, there is only one weak clockwise vortex in the middle of the square enclosure, and the distribution of isotherms is pretty similar to the cases of pure gravity convection. The influence of magnetic buoyancy force can not be neglected when the magnetic field is powerful enough, such as γ=10 and γ=50. In the upper part of the square cavity, the fluid near the cold wall has a stronger upward magnetic buoyancy force than the fluid near the hot wall, due to a larger magnetic susceptibility, so there is a tendency which will result in an anticlockwise flow, while the gravity plays an opposite role. Thus, once the magnetic buoyancy force overcomes the gravitational buoyancy force, the combined action of these two buoyancy will lead to a weak anticlockwise vortex near the top right corner. In the lower part, the cold fluid has a stronger downward magnetic buoyancy force than the hot fluid which causes
a clockwise vortex and the gravitational buoyancy force enhances the intensity of the clockwise vortex although it shrinks a little compared with the case at γ=1. Distinct temperature gradients gradually form at the bottom of left hot wall and the middle of right cold wall, which suggests an more efficient heat transfer rate. When the magnetic field continues to grow and reaches to γ=1000, the magnetic buoyancy force completely exceeds the gravitational buoyancy force, thus, the streamlines and isotherms are almost symmetric about the horizontal centerline. A clockwise vortex and a anticlockwise one nearly cover all the enclosure and the flow intensity is remarkable. At γ=1000, the temperature gradients are clearly observed at the upper and lower position of the hot wall, and the middle of the cold wall. Isotherms are nearly the same to the cases of pure magnetic convection because of the absolute predominance of the magnetic buoyancy force, which declares an excellent heat transfer performance.
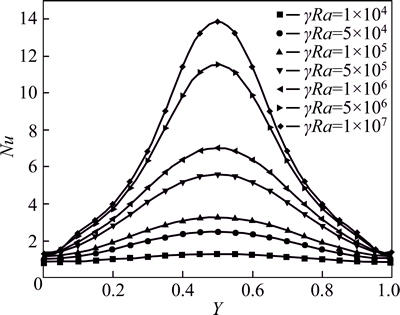
Fig. 5 Effect of γRa on local Nusselt number of right wall under non-gravitational conditions.
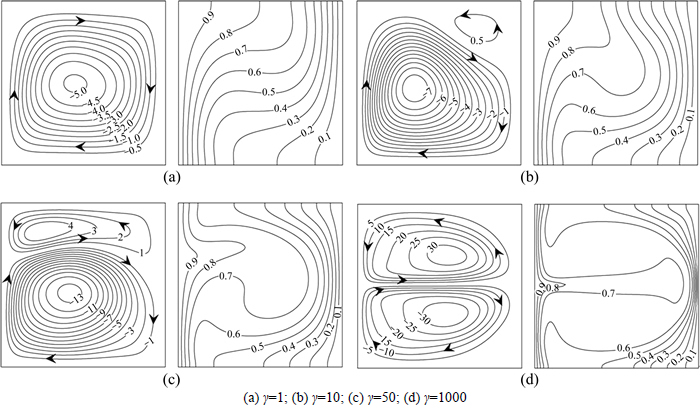
Fig. 6 Effect of magnetic force number on streamlines and isotherms:
Figure 7 shows the variation of local Nusselt number on the left wall for various magnetic force numbers. It can be observed that the local Nusselt number increases with the increase of magnetic force number on the lower part of hot wall. On the upper part, the local Nusselt number goes down at first and then increases when the value of γ is larger. It can also be found that when γ is small, such as γ=1, 5 and 10, a downtrend of the variation is observed with the increasing height of left hot wall. When magnetic force number is large enough, symmetric curves of the local Nusselt number are obtained. The curves of the right cold wall are described in Fig. 8. Although some curves intersect with each other, the local Nusselt number on right wall generally grows with the augment of γ. When γ reaches to 50 or more, these single peak curves are approximately symmetric, similar to the pure magnetic convection cases.
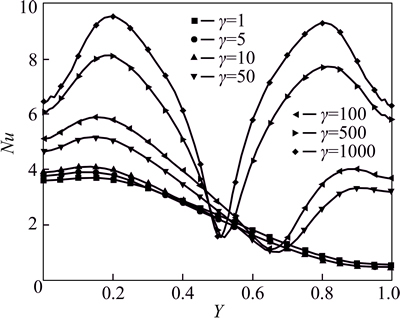
Fig. 7 Effect of γ on local Nusselt number of left vertical wall
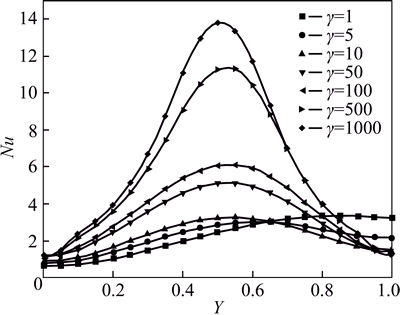
Fig. 8 Effect of γ on local Nusselt number of right vertical wall
5.3 Comparison between non-gravitational and gravitational conditions
Comparison of the average Nusselt numbers under gravitational as well as non-gravitational condition is illustrated in Fig. 9. For simplicity, the parameter γRa is used to describe the strength of magnetic quadrupole field. It can be observed that the average Nusselt number on vertical walls generally grows with the increasing value of γRa whether there is gravity or not. Under non-gravitational condition, the curve is clearly more smooth than the other one, and the growth of Num slows down gradually once γRa reaches about 1×106. Under gravitational condition, when γRa is relatively small as from 1×104 to 1×105, the average Nusselt number is obviously larger and the curve slightly goes down at first, and then, it raises with the augment of γRa. According to the figure below, it can be found that the heat transfer performance under gravitational condition is more efficient when the magnetic field is pretty weak, but later, this ascendance disappears for higher γRa values. Thus, there is an intersection point near γRa=1×105 which declares the same overall heat transfer rate of these two cases. With the enhancement of magnetic field, the difference between these two curves becomes significant, which indicates that the gravitational buoyancy force starts to perform negative influence on the convective heat transfer. A significant down-warping is spotted on the lower curve because of the effect of gravity. Ultimately, there is no evident difference between both curves anymore when γRa is more than 4×106. So, the influence of gravity can be negligible. These two curves of average Nusselt number nearly show linear change with the increasing value of γRa.
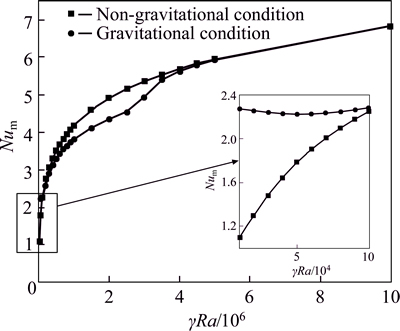
Fig. 9 Comparison of average Nusselt numbers under both conditions for various γRa
6 Conclusions
Thermomagnetic convection of paramagnetic fluid in a two-dimensional square cavity under a magnetic quadrupole field is numerically investigated using LBM. The flow structure and convective heat transfer are carefully compared under gravitational and non- gravitational conditions for various magnetic force numbers. Results show that the flow under non- gravitational environment presents a two-cellular structure, consisting of a clockwise vortex and an anticlockwise vortex. While the flow under gravitational condition presents a weak clockwise vortex at first, and then a symmetric stratification phenomenon when the magnetic force number is relatively large. The Nusselt numbers on the left and right walls are obviously influenced by the magnetic and gravitational buoyancy forces. The convective heat transfer is more efficient under gravitational condition when the magnetic field is pretty weak, while the opposite situation happens at γRa higher than 1×105.
Nomenclature
b
Magnetic flux density (T)
b0
Reference magnetic flux density (T)
B
Dimensionless reference magnetic flux density
B0
Remanence of permanent magnets (T)
c
Lattice speed
ek
Discrete speeds
f
Density distribution functions
fx
Body force in x-direction
fy
Body force in y-direction
feq
Equilibrium density distribution functions
Fx
Dimensionless body force in x-direction
Fy
Dimensionless body force in y-direction
Fk
Dimensionless body force term
g
Gravitational acceleration (m·s-2)
g
Internal energy distribution functions
geq
Equilibrium internal energy distribution functions
Ha
Hartmann number
k
Lattice number
L
Length of the enclosure (m)
L1
Length of the permanent magnets (m)
L2
Distance between two opposite permanent magnets (m)
Num
Average Nusselt number
p
Pressure, Pa
P0
Pressure at reference temperature , Pa
p'
Pressure difference due to the perturbed state, Pa
P
Dimensionless pressure
Pr
Prandtl number, 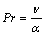
Ra
Rayleigh number, 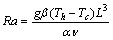
T0
Reference temperature, 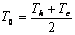 (K)
(K)
Tc
Cold wall temperature (K)
T
Fluid temperature (K)
Th
Hot wall temperature (K)
u,v
Velocity components (m·s-1)
U,V
Dimensionless velocity components
U
Velocity vector
x,y
Cartesian coordinates (m)
X,Y
Dimensionless Cartesian coordinates
Greek symbol
α
Thermal diffusivity (m·s-1)
β
Thermal expansion coefficient (K-1)
γ
Dimensionless magnetic flux density, 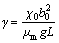
θ
Dimensionless temperature, 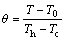
μm
Magnetic permeability (H·m-1)
μ
Dynamic viscosity (kg·m-1·s-1)
ν
Kinematic viscosity (m2·s-1)
ρ
Density (kg·m-3)
ρ0
Fluid density at reference temperature (kg·m-3)
χ0
Mass magnetic susceptibility (m3·kg-1)
ωk
Weighted factor
ωm
Weighted factor for momentum equations
ωs
Weighted factor for scalar equations
Δt
Time step
Subscripts
0
Reference value
c
Cold
h
Hot
References
[1] GHASEMI B, AMINOSSADATI S M, RAISI A. Magnetic field effect on natural convection in a nanofluid-filled square enclosure [J]. International Journal of Thermal Sciences, 2011, 50: 1748-1756.
[2] AL-ZAMILY A M J. Effect of magnetic field on natural convection in a nanofluid-filled semi-circular enclosure with heat flux source [J]. Computers & Fluids, 2014, 103: 71-85.
[3] SANKAR M, VENKATACHALAPPA M, SHIVAKUMARA I S. Effect of magnetic field on natural convection in a vertical cylindrical annulus [J]. International Journal of Engineering Science, 2006, 44: 1556-1570.
[4] SANKAR M, VENKATACHALAPPA M, DO Y. Effect of magnetic field on the buoyancy and thermocapillary driven convection of an electrically conducting fluid in an annular enclosure [J]. International Journal of Heat and Fluid Flow, 2011, 32: 402-412.
[5] KUO J S, LEONG J C. Analysis of a conducting fluid in a thin annulus with rotating insulated walls under radial magnetic effect [J]. Applied Mathematical Modelling, 2013, 37: 3021-3035.
[6] PIRMOHAMMADI M, GHASSEMI M. Effect of magnetic field on convection heat transfer inside a tilted square enclosure [J]. International Communications in Heat and Mass Transfer, 2009, 36: 776-780.
[7] SATHIYAMOORTHY M, CHAMKHA A. Effect of magnetic field on natural convection flow in a liquid gallium filled square cavity for linearly heated side wall(s) [J]. International Journal of Thermal Sciences, 2010, 49: 1856-1865.
[8] YU P X, QIU J X, QIN Q, TIAN Z F. Numerical investigation of natural convection in a rectangular cavity under different directions of uniform magnetic field [J]. International Journal of Heat and Mass Transfer, 2013, 67: 1131-1144.
[9] ELSHEHABEY H M, HADY F M, AHMED S E, MOHAMED R A. Numerical investigation for natural convection of a nanofluid in an inclined L-shaped cavity in the presence of an inclined magnetic field [J]. International Communications in Heat and Mass Transfer, 2014, 57: 228-238.
[10] ASHOURI M, EBRAHIMI B, SHAFII M B, SAIDI M H, SAIDI M S. Correlation for Nusselt number in pure magnetic convection ferrofluid flow in a square cavity by a numerical investigation [J]. Journal of Magnetism and Magnetic Materials, 2010, 322: 3607-3613.
[11] LI Qiao-jie, ZHENG Zhou-shun, WANG Shuang, LIU Jian-kang. Numerical simulation of powder flow in high velocity compaction by lattice Boltzmann method [J]. The Chinese Journal of Nonferrous Metals, 2012, 22(6): 1754-1762. (in Chinese)
[12] SU Qing, CHEN Ai-rong, ZHAO Tie-jun. Carbonation of sea sand concrete [J]. Journal of Central South University: Science and Technology, 2012, 42(1): 304-309. (in Chinese)
[13] MOHAMAD A A, KUZMIN A. A critical evaluation of force term in lattice Boltzmann method, natural convection problem [J]. International Journal of Heat and Mass Transfer, 2010, 53: 990-996.
[14] LI Zheng, YANG Mo, ZHANG Yu-wen. A coupled lattice Boltzmann and finite volume method for natural convection simulation [J]. International Journal of Heat and Mass Transfer, 2014, 70: 864-874.
[15] SHEIKHOLESLAMI M, GORJI-BANDPY M, GANJI D D. Numerical investigation of MHD effects on Al2O3-water nanofluid flow and heat transfer in a semi-annulus enclosure using LBM [J]. Energy, 2013, 60: 501-510.
[16] SHEIKHOLESLAMI M, GORJI-BANDPY M, GANJI D D. Lattice Boltzmann method for MHD natural convection heat transfer using nanofluid [J]. Powder Technology, 2014, 254: 82-93.
[17] SHEIKHOLESLAMI M, GORJI-BANDPY M, VAJRAVELU K. Lattice Boltzmann simulation of magnetohydrodynamic natural convection heat transfer of Al2O3-water nanofluid in a horizontal cylindrical enclosure with an inner triangular cylinder [J]. International Journal of Heat and Mass Transfer, 2015, 80: 16-25.
[18] KEFAYATI GH R. Effect of a magnetic field on natural convection in an open cavity subjugated to water/alumina nanofluid using Lattice Boltzmann method [J]. International Communications in Heat and Mass Transfer, 2013, 40: 67-77.
[19] KEFAYATI G H R. Lattice Boltzmann simulation of MHD natural convection in a nanofluid-filled cavity with sinusoidal temperature distribution [J]. Powder Technology, 2013, 243: 171-183.
[20] NEMATI H, FARHADI M, SEDIGHI K, ASHORYNEJAD H R, FATTAHI E. Magnetic field effects on natural convection flow of nanofluid in a rectangular cavity using the Lattice Boltzmann model [J]. Scientia Iranica, 2012, 19(2): 303-310.
[21] NEMATI H, FARHADI M, SEDIGHI K, FATTAHI E, DARZI A A R. Lattice Boltzmann simulation of nanofluid in lid-driven cavity [J]. International Communications in Heat and Mass Transfer, 2010, 37: 1528-1534.
[22] KEFAYATI G H R, GORJI-BANDPY M, SAJJADI H, GANJI D D. Lattice Boltzmann simulation of MHD mixed convection in a lid-driven square cavity with linearly heated wall [J]. Scientia Iranica B, 2012, 19(4): 1053-1065.
[23] XUAN Yi-min, LI Qiang, YE Meng. Investigations of convective heat transfer in ferrofluid microflows using lattice-Boltzmann approach [J]. International Journal of Thermal Sciences, 2007, 46: 105-111.
[24] HUSSEIN A K, ASHORYNEJAD H R, SHIKHOLESLAMI M, SIVASANKARAN S. Lattice Boltzmann simulation of natural convection heat transfer in an open enclosure filled with Cu–water nanofluid in a presence of magnetic field [J]. Nuclear Engineering and Design, 2014, 268: 10-17.
[25] MAHMOUDI A, MEJRI I, ABBASSI M A, OMRI A. Lattice Boltzmann simulation of MHD natural convection in a nanofluid-filled cavity with linear temperature distribution [J]. Powder Technology, 2014, 256: 257-271.
[26] SHEIKHOLESLAMI M, GORJI-BANDPY M. Free convection of ferrofluid in a cavity heated from below in the presence of an external magnetic field [J]. Powder Technology, 2014, 256: 490-498.
[27] KEFAYATI GH R. Natural convection of ferrofluid in a linearly heated cavity utilizing LBM [J]. Journal of Molecular Liquids, 2014, 191: 1-9.
[28] YANG Li-jun, REN Jian-xun, SONG Yao-zu, GUO Zeng-yuan. Free convection of a gas induced by a magnetic quadrupole field [J]. Journal of Magnetism and Magnetic Materials, 2003, 261: 377-384.
[29] YANG Li-jun, REN Jian-xun, SONG Yao-zu, MIN Jing-chun, GUO Zeng-yuan. Convection heat transfer enhancement of air in a rectangular duct by application of magnetic quadrupole field [J]. International Journal of Engineering Science, 2004, 42: 491-507.
[30] HUELSZ G, RECHTMAN R. Heat transfer due to natural convection in an inclined square cavity using the lattice Boltzmann equation method [J]. International Journal of Thermal Sciences, 2013, 65: 111-119.
[31] CONTRINO D, LALLEMAND P, ASINARI P, LUO Li-shi. Lattice Boltzmann simulations of the thermally driven 2D square cavity at high Rayleigh numbers [J]. Journal of Computational Physics, 2014, 275: 257-272.
[32] MEHRIZI A A, SEDIGHI K, FARHADI M, SHEIKHOLESLAMI M. Lattice Boltzmann simulation of natural convection heat transfer in an elliptical-triangular annulus [J]. International Communications in Heat and Mass Transfer, 2013, 48: 164-177.
[33] TAGAWA T,SHIGEMITSU R,OZOE H. Magnetizing force modeled and numerically solved for natural convection of air in a cubic enclosure: effect of the direction of the magnetic field [J]. International Journal of Heat and Mass Transfer, 2002, 45: 267-277.
[34] DAVIS G D V. Natural convection of air in a square cavity, a benchmark numerical solution [J]. International Journal Numerical Methods Fluids, 1962, 3: 249-264.
(Edited by DENG Lü-xiang)
Cite this article as:
XIE Nan, JIANG Chang-wei, HE Yi-hai, YAO Ming. Lattice Boltzmann method for thermomagnetic convection of paramagnetic fluid in square cavity under a magnetic quadrupole field [J]. Journal of Central South University, 2017, 24(5): 1174-1182.
DOI:https://dx.doi.org/10.1007/s11771-017-3520-yFoundation item: Project(11572056) supported by the National Natural Science Foundation of China; Project(15A006) supported by the Scientific Research Fund of Hunan Provincial Education Department, China
Received date: 2015-10-11; Accepted date: 2016-03-31
Corresponding author: JIANG Chang-wei, PhD, Professor; Tel/Fax: +86-731-85258409; E-mail: cw_jiang@163.com
Abstract: Numerical study was performed for a better understanding on thermomagnetic convection under magnetic quadrupole field utilizing the lattice Boltzmann method. Present problem was examined under non-gravitational and gravitational conditions for a wide range of magnetic force number from 0 to 1000. Vertical walls of the square cavity were heated differentially while the horizontal walls were assumed to be adiabatic. Distributions of the flow and temperature field were clearly illustrated. Under non-gravitational condition, the flow presents a two-cellular structure with horizontal symmetry, and the average Nusselt number increases with the augment of magnetic force number. Under gravitational condition, two-cellular structure only occurs when the magnetic field is relatively strong, and the average Nusselt number decreases at first and then rises with the enhancing magnetic field. Results show that the magnetic field intensity and the Rayleigh number both have significant influence on convective heat transfer, and the gravity plays a positive role in heat transfer under weak magnetic field while a negative one for magnetic force numbers larger than 1×105.


