无网格法在大地电磁正演计算中的应用

严家斌，李俊杰

(中南大学 地球科学与信息物理学院，湖南 长沙，410083)

摘 要：

基本原理及二维大地电磁变分问题的无网格解法，对比3层介质模型相同数量节点下无网格法与有限元法计算精度的差异，研究支持域量纲为1的尺寸与高斯点数量对大地电磁场计算精度的影响，最后通过二维模型的计算进一步验证算法的有效性。研究结果表明：无网格法计算MT问题效果很好；在相同节点个数下无网格法精度比有限元法的精度高；支持域量纲为1的尺寸对其计算精度影响很大，较优值为1.0~1.2；高斯点数量对精度影响较小，2点高斯公式能满足精度要求。

关键词：

无网格法；大地电磁；有限元法；支持域；高斯点；

中图分类号: P631          文献标志码：A         文章编号：1672-7207(2014)10-3513-08

Magnetotelluric forward calculation by meshless method

YAN Jiabin, LI Junjie

(School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)

Abstract: The basic principles of the meshless method and its application to two-dimensional magnetotelluric forward were described, and calculation accuracy difference of finite element method for three medium model in the same number of nodes was compared. Algorithm’s calculation accuracy in different support domain dimensionless sizes and different numbers of gauss points were researched. Finally, the effectiveness of the algorithm was verified through two-dimensional model calculations. The results show that meshless method has a good effect on solving magnetotelluric forward problem and is more accurate than the finite element method in the same number of nodes. Support domain dimensionless size is an important parameter to meshless method, and its proposed value is from 1.0 to 1.2; the number of gauss points has little effect on calculation accuracy and two-point Gaussian formula can meet the requirement.

Key words: meshless method; magnetotelluric; finite element method; support domain; Gauss points

大地电磁测深法(MT)利用天然交变电磁场研究地球电性结构，对低阻层分辨率高，勘探深度大^[1]。正演计算是研究其场分布规律的基础，有限元法作为经典的网格数值方法有坚实的理论基础和数学证明，且适用于复杂物性分布和复杂边界形状的计算，在地球物理电磁法领域应用广泛，其最大缺陷在于求解高维问题时网格生成复杂。此外，某些复杂问题用有限元法求解较困难，这些问题主要包括超大变形问题、动态裂纹扩展问题、金属材料成型问题、高速冲击及大爆炸问题。用有限元法求解这些问题时，由于巨大的网格畸变或单元分裂，计算时必须不断重新划分网格，极大地增加了计算时间，并且有时重新划分网格并不能完全解决问题^[2]。要从根本上解决有限元法的缺陷就必须避免使用事先定义的网格，无网格的思想由此诞生。无网格法^[3-5]通过局部支持域内的节点构造形函数及建立离散系统方程，是一种基于节点的数值方法。该方法避免了网格生成困难问题，构造高阶形函数方便，自适应分析容易，不但广泛应用于有限元法所触及的领域，而且解决了许多网格方法难以处理的问题^[6-9]，现已成为计算力学领域的研究热点，然而，其在地球物理学领域的研究很少^[10-14]。前人的研究工作主要验证了无网格法计算地球物理场响应的有效性，但没有突出无网格法较其他网格方法的优越之处。为此，本文作者以大地电磁二维问题为例，介绍无网格法的基本原理及相应的求解过程，验证无网格法求解MT问题的有效性，对比相同节点个数下无网格法与有限元法的计算精度，并对影响其精度的因素进行分析。

1  二维大地电磁边值问题与变分问题

当地下电性结构为二维时，取走向为Z轴，X轴与Z轴垂直，Y轴垂直向上。求解域为矩形区域，4个顶点依次以ABCD顺时针编号，Γ₁为地质体与周围介质的边界。

当平面电磁波以任何角度入射地面时，地下介质中的电磁波总以平面波形式几乎垂直地向下传播，满足如下边值问题^[15]：

   (1)

式中：▽为二维哈密顿算子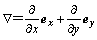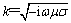，；。对于电场极化模式(TE模式)，有

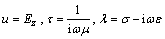        (2)

对于磁场极化模式(TM模式)，有

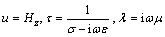        (3)

式中：ω为角频率；μ为磁导率；σ为电导率；ε为介电常数。对式(1)运用变分原理，可导出其对应的变分问题^[15]：

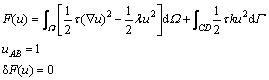 (4)

2  二维大地电磁变分问题的无网格解法

无网格法利用位于积分点支持域内的场节点构造形函数，常用形函数的构造方法有移动最小二乘近似^[16-18]、核积分近似^[19-20]、点插值近似^[21]及径向基函数近似^[22]，其中移动最小二乘近似(MLS)能够通过权函数的适当选取来得到具有高阶连续性的形函数，本文采用此种近似方式。图1所示为无网格法背景网格、支持域、积分点与场节点示意图。由于背景网格的积分常选用高斯积分法，故积分点又称高斯积分点或高斯点。

图1  无网格法背景网格、支持域、积分点与场节点示意图

Fig. 1  Diagrams of background grid,support domain, Gauss points and nodes in meshless method

2.1  支持域

支持域示意图如图1所示。常用的支持域形状有圆形与矩形2种，对于任一高斯点X_Q，其支持域尺寸d由下式确定：

               (5)

式中：α为支持域量纲为1的尺寸，它用于控制实际支持域的大小，是对无网格法计算精度影响很大的参数^[5]；d_c为位于高斯点X_Q附近的平均结点间距，

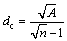              (6)

A为预估的支持域面积；n为包含在A中的节点数。对于节点均匀分布的情况，d_c为节点间距。本文采用矩形支持域，故有2个方向的支持域尺寸，即

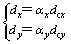             (7)

式中：d_cx与d_cy分别为横纵向节点间距；α_x与α_y为对应的支持域的量纲为1的尺寸。为便于程序设计，研究中常取α_x=α_y=α。

2.2  移动最小二乘近似(moving least-square，MLS)

定义求解域Ω中任意一点X处的场变量u(X)近似表达式为^[16]

    (8)

式中：p(X)为二维空间坐标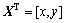的基函数可用Pascal三角形确定；系数向量为X的函数；m为单项式的个数。对于一维(1D)和二维(2D)空间，其线性基函数分别为

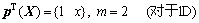
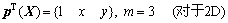
其二次基函数分别为

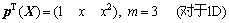
系数向量a(X)可通过如下的加权残差法求得：

     (9)

式(9)中的为权函数，它对MLS的近似性能有至关重要的影响。权函数的选择需具备如下性质^[5]：1) 支持域内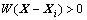；2) 支持域外；3) 从计算点X开始单调递减；4) 应足够光滑，尤其是在边界上。本文选择3次样条函数为权函数，其表达式为

   (10)

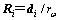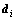式中：；为节点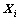与采样点X之间的距离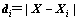，；为权函数支持域尺寸。通过式(9)运算得出如下线性关系：

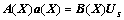        (11)

式中：为支持域内所有节点的节点场函数向量；

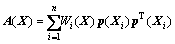    (12)

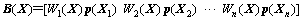   (13)

式(12)中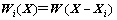,求解式(11)可得

       (14)

将式(14)代入式(8)得

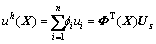     (15)

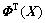即为计算点X在支持域内的MLS形函数。节点i的形函数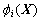表达式为

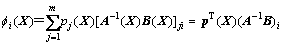 (16)

2.3  无网格离散系统方程的构造

定义了无网格形函数，便可以构造式(4)的离散系统方程。将变分符号代入式(4)，有

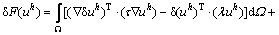
        (17)

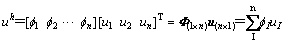   (18)

式中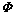：为形函数矩阵；n为支持域内的节点数；u为支持域内n个节点的场向量。对式(18)进行变分运算，有

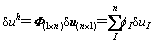       (19)

将式(19)与式(18)代入式(17)，式(4)变为如下形式：

         (20)

式(20)采用支持域内n个场节点编号。对于求解域内所有场节点还应有一个用于将局部节点矩阵组装成总体刚度矩阵的总体编号体系。当节点I和节点J位于不同支持域时，其相应的被积函数为0，因此，可得到按求解域节点编号的总体编号体系方程：

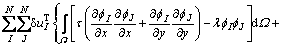
        (21)

式(21)可简写为

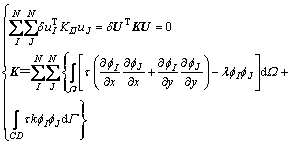  (22)

由于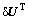是任意的，故式(22)成立的条件为

KU=0               (23)

式(23)即为无网格法构造的系统方程。

2.4  求解域背景网格积分

K的表达式中包含对求解域Ω与求解域边界Γ的积分。为计算这些积分，需将求解域离散成一组背景网格(图1)。总体积分可表示成这些单元积分之和的形式，每个单元的积分利用高斯积分法求解，有

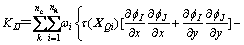
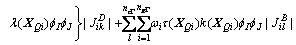  (24)

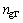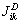式中：n_c与分别为背景单元及边界单元的个数；n_g与分别为背景单元及边界单元内的高斯点数目；为第i个高斯点的权系数；与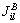分别为背景单元k在积分点处面积分及子边界l在积分点处曲线积分的雅可比(Jacobian)矩阵。

式(24)即为总体刚度矩阵的最终离散表达式，它是带状、对称、稀疏的^[17]。在无网格法中，各矩阵的组装均基于高斯点，不同高斯点对应的形函数可能不同，每次积分都会重新构造形函数，这与有限元法有很大不同。有限元法中同一单元内的所有高斯点均采用相同的节点进行插值运算。

背景网格积分是无网格法中最重要的数值计算问题之一，总积分点数一般取支持域内场节点的数量的3~9倍^[16-18]。本文中每个背景单元采用4(即2×2)个高斯点，每个边界单元采用2个高斯点，也能取得较高的精度。

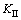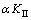求解线性方程组KU=0还需加载边界条件。常用边界条件的加载方法有罚函数法^[21]和Lagrange乘子法^[17]。Lagrange乘子法虽能准确地加载边界条件，但增加了未知量的数目及刚度矩阵的维数^[17]。本文采用简单易行的罚函数法加载边界条件，将刚度矩阵中相应的对角元素变为(其中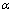为惩罚系数，其值可取10⁴~10¹⁰)，然后将边界上的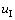取代方程组右端的零向量即可。

3  数值计算与精度对比

研究3层介质模型：第1层电阻率ρ₁=400 Ω·m,层厚度h₁=1 km；第2层电阻率ρ₁=1 500 Ω·m , 层厚度h₂=3 km；第3层电阻率ρ₃=150 Ω·m，层厚h₃=4 km。场节点等间距分布于问题域，对于TE模式，使用3 321(即41×81)个场节点，3 200(即40×80)个背影网格，横向节点间距为100 m，纵向节点间距为200 m。对于TM模式，使用1 681(即41×41)个场节点，1 600(即40×40)个背影网格，节点间距与TE模式的相同。有限元法节点的分布与无网格法的一致。

图2(a)所示为无网格法与有限元法视电阻率计算结果与解析解对比结果，图2(b)所示为相应的相对误差曲线。从图2(a)可见：当频率f＜10² Hz时，这2种方法计算曲线形态均与解析解的一致，表明无网格法在大地电磁正演计算中的有效性；当f＞10² Hz时，TE模式与TM模式曲线开始与解析解出现偏差，TE模式曲线向解析解下方偏移；TM模式反之，且偏差随着频率的增高而增大；无网格法计算曲线与有限元法所得曲线一致。无网格法计算精度随频率的增高而降低，相对误差变化范围为10^-8~0.03，在10^-3 ~25 Hz频段，无网格法计算精度比有限元法的高，在25 ~10³ Hz频段，精度与有限元法的相当。有限元法计算精度呈现一定起伏，相对误差变化范围为4×10^-4~0.03，在10^-3 ~10^-1 Hz与20 ~10³ Hz频段，有限元法精度随频率的增高而降低；在10^-1 ~10 Hz频段，精度随频率的增高而增高；在10~20 Hz频度较稳定，且精度达到最高(如图2(b)所示)。

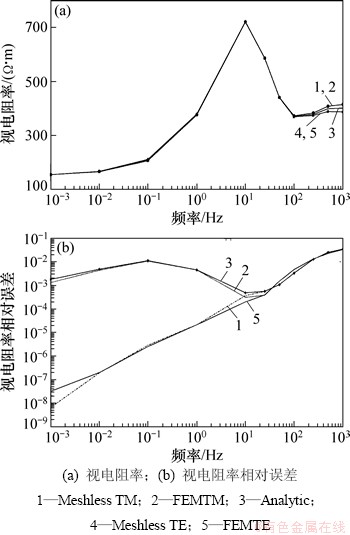
图2  无网格法与有限元法视电阻率计算结果与解析解对比图及相应的相对误差曲线

Fig. 2  Comparison of apparent resistivity numerical results and their relative errors by meshless method and finite element method with analytical solutions

图3(a)所示为无网格法与有限元法视相位计算结果与解析解对比结果，图3(b)所示为相应的相对误差曲线。从图3(a)可见：在频率小于250 Hz的频段，数值计算曲线形态与解析解的一致；在频率大于250 Hz的频段，TE模式曲线向解析解上方偏移，而TM模式反之。

无网格法计算精度基本呈现随频率的增高而降低的趋势，精度变化范围为6×10^-9~0.06，这2种模式的精度曲线在10^-3~10 Hz频段相近；当频率f＞10 Hz时，这2种模式精度曲线开始出现差异；在50 Hz频点附近，TE模式与TM模式曲线分别出现相应的极大和极小值，在100 Hz频点附近TE模式曲线呈现极小值；当频率f＞200 Hz时,精度曲线重新归于一致。有限元法精度曲线呈现轻微起伏，相对误差变化范围为10^-3~0.06，这2种模式精度曲线出现差异的频段及曲线极值点对应的频点均与无网格法的相同(如图3(b)所示)。

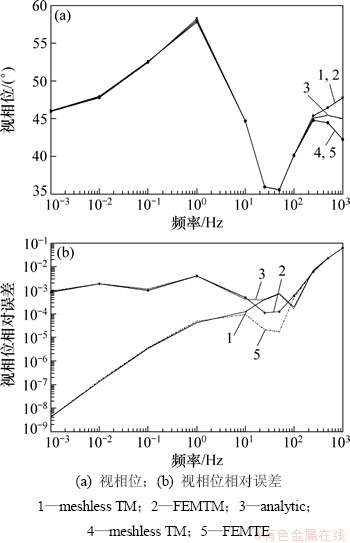
图3  无网格法与有限元法视相位计算结果与解析解对比图及相应的相对误差曲线

Fig. 3  Comparison of apparent phase numerical results and their relative errors by meshless method and finite element method with analytical solutions

以上分析结果表明：在中低频段(f＞20 Hz)，无网格法计算精度比有限元法的精度高；当高于20 Hz时，这2种方法计算精度相当；无网格法比有限元法更适合于低频段的计算，有限元法对中频段的计算精度比低频段与中高频段的精度高。

图4所示为四点高斯公式不同支持域尺寸的无网格法计算结果。从如图4(a)可见：随着频率的增高，不同支持域尺寸的TE模式曲线相继向下偏离解析解，且支持域尺寸越大，偏离现象越明显；当支持域量纲为1的尺寸α=2时，其尾支电阻率接近300 Ω·m，与解析解相差近100 Ω·m，可见支持域量纲为1的尺寸α对无网格法计算精度影响很大。

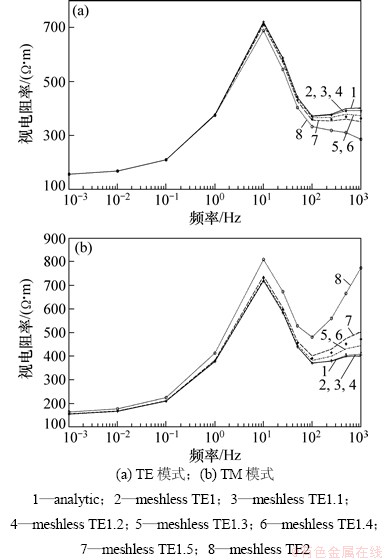
图4  四点高斯公式不同支持域尺寸的无网格法TE模式与TM模式视电阻率计算结果

Fig. 4  TE mode and TM mode calculation results of apparent resistively in different support domain size with four-point gauss formula by meshless method

TM模式曲线偏离规律与TE模式的类似，不同之处在于TM模式曲线向上偏离解析解，且偏差较TE模式明显(如图4(b)所示)，这2种模式下支持域量纲为1的尺寸最佳选择区间均为α=1.0~1.2。

图5所示为支持域量纲为1的尺寸为1.0时，不同数量高斯点公式的无网格法视电阻率计算结果；表1所示为相应的计算时间及有限元法耗时。从图5可见：在这2种模式下，不同数量高斯无网格法计算结果曲线基本一致，4~6点高斯无网格法对中高频段计算精度相对较高，高斯点数量的增加不能显著提高计算精度，但对无网格法计算效率影响很大，2点高斯公式计算耗时约比有限元法高1个数量级(表1)。综合考虑计算效率与精度，建议用2~4点高斯公式，本文中支持域的量纲为1的尺寸α=1.0，选用2点高斯公式。

为了进一步说明无网格法求解MT问题的有效性，对图6所示的二维模型进行计算：围岩电阻率ρ₁=1 kΩ·m，柱形二度异常体电阻率ρ₂=1 kΩ·m，圆形截面半径R=200 m，圆心到地面的距离h=1 200 m。场节点均匀分布于求解域，TE模式为41×81个场节点，TM模式为41×41个场节点。无网格法中模型参数的加载基于高斯积分点而非单元，高斯点的位置可由坐标确定，该特性使其在复杂地质模型构建上较常规网格方法方便。图7(a)与图7(b)所示分别为TE模式及TM模式下图6模型的计算结果。从图7可见：TE模式异常横向拉长，TM模式异常纵向拉长，这2种模式均很好地反映了低阻异常体的存在。

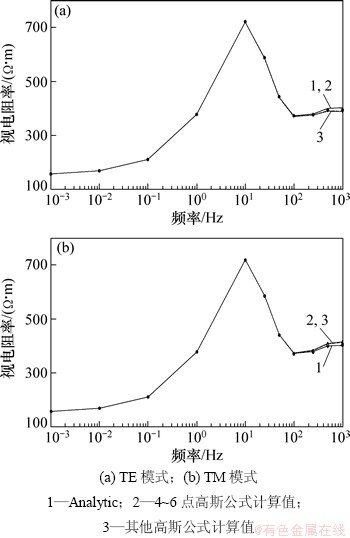
图5  支持域量纲为1的尺寸为1.0时不同数量高斯点公式的无网格法TE模式与TM模式视电阻率计算结果

Fig. 5  TE mode and TM mode calculation results of apparent resistivity in different numbers of gauss points by meshless method when support domain dimensionless size is 1.0

表1  支持域量纲为1的尺寸为1.0时无网格法计算时间及有限法耗时

Table 1  Calculation time of meshless method when support domain dimensionless size is 1.0     s

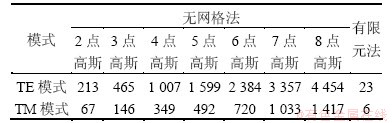
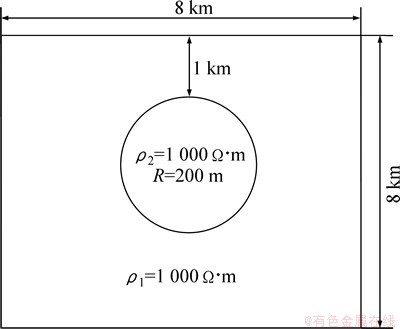
图6  数值模型

Fig. 6  Numerical model

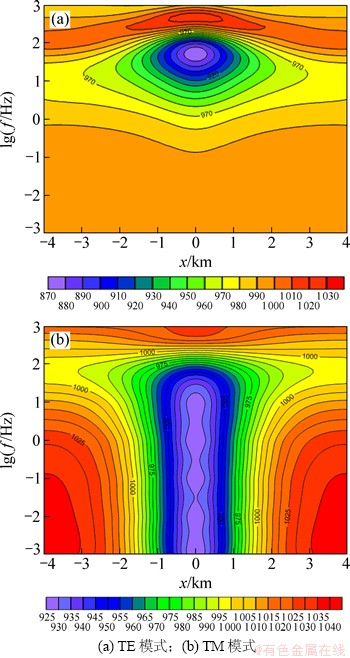
图7  二维地质模型TE模式与TM模式视电阻率计算结果

Fig. 7  TE mode and TM mode calculation results of apparent resistivity in two-dimensional model

4  结论

1) 将无网格法应用于大地电磁正演计算，介绍了无网格法基本原理及变分问题的无网格求解过程，数值计算结果验证了无网格法在大地电磁正演计算中的有效性。

2) 无网格法适用于大地电磁正演计算，其计算精度很高，精度最高可达10^-9数量级，最低也达0.03；在频率小于20 Hz的中低频段无网格法计算精度比有限元法的高，大于此频点，精度与有限元法的相当。

3) 复杂地质模型电磁响应的计算一般需采用非结构化网格，此种网格的生成算法较复杂。本文采用节点规则分布的无网格法计算了柱形二度体的电磁响应，TE模式与TM模式等值线图均很好地反映出异常体的存在；无网格法在地质模型构建上具有较大随意性，这也是节点方法较常规网格方法最大的优势之一。

4) 支持域量纲为1的尺寸α作为无网格法构建形函数的重要参数，其对无网格法计算精度影响很大，当α=1.0~1.2时精度较高。

5) 高斯积分法是求解无网格背景单元积分的常用方法，高斯点数量对无网格法计算效率影响很大，对计算精度影响较小，2~4点高斯公式能达到精度要求。

6) 无网格法计算时间主要花费在数值积分及无网格形函数的构造上，耗时约比有限元法高1个数量级。对无网格并行算法的研究会成为今后的研究热点。

参考文献：

[1] 刘国兴. 电法勘探原理与方法[M]. 北京: 地质出版社, 2005: 164-172.

LIU Guoxing. Electrical prospecting theory and methods[M]. Beijing: Geological Press, 2005: 164-172.

[2] 顾元通, 丁桦. 无网格法及其最新进展[J]. 力学进展, 2005, 35(3): 323-337.

GU Yuantong, DING Hua. Recent developments of meshless method[J]. Advances in Mechanics, 2005, 35(3): 323-337.

[3] 张雄, 刘岩. 无网格法[M]. 北京: 清华大学出版社, 2004: 1-15.

ZHANG Xiong, LIU Yan. Meshless method[M]. Beijing: Tsinghua University Press, 2004: 1-15.

[4] Liu G R, Liu M B. Smoothing particle Hydrodynamic Methods: A Meshfree Particle Method[M]. Singapore: World Scientific Publishing Company, 2003: 1-17.

[5] Liu G R, Gu Y T. An Introduction to meshfree methods and their programming[M]. Berlin: Springer, 2005: 23-32.

[6] Wang S L N. A large-deformation Galerkin SPH method for fracture[J]. J Eng Math, 2011, 71(3): 305-318.

[7] 马泽玲, 虎旭林. 三维无单元法模拟裂纹扩展[J]. 宁夏大学学报(自然科学版), 2011, 32(1): 35-38.

MA Zeling, HU Xulin. Simulation of fracture propagation by three-dimensional element-free method[J]. Journal of Ningxia University (Natural Science Edition), 2011, 32(1): 35-38.

[8] LIU Hongsheng, XING Zhongwen, YANG Yuying. Simulation of sheet metal forming process using reproducing kernel particle method[J]. Int J Numer Meth Bio, 2010, 26(11): 1462-1476.

[9] 贝新源, 岳宗五. 三维SPH程序及其在斜高速碰撞问题的应用[J]. 计算物理, 1997, 14(2): 155-166.

BEI Xinyuan, YUE Zongwu. A study on three-dimensioal SPH[J]. Chinese Journal of Computational Physics, 1997, 14(2): 155-166.

[10] 贾晓峰, 胡天跃. 滑动最小二乘法求解地震波波动方程[J]. 地球物理学进展, 2005, 20(4): 920-924.

JIA Xiaofeng, HU Tianyue. Solving seismic wave equation by moving least squares(MLS) method[J]. Progress in Geophysics, 2005, 20(4): 920-924.

[11] 贾晓峰. 复杂介质中地震波模拟与成像的无单元数值算法[D]. 北京: 北京大学地球与空间科学院, 2005: 1-50.

JIA Xiaofeng. Element-free Galerkin method for seismic numerical modeling and imaging in complex media[D]. Beijing: Peking University. Earth and Space Sciences, 2005: 1-50.

[12] 王月英. 地震波正演模拟中无单元Galerkin法初探[J]. 地球物理学进展, 2007, 22(5): 1539-1544.

WANG Yueying. Study of element-free galerkin method in the seismic forward modeling[J]. Progress in Geophysics, 2007, 22(5): 1539-1544.

[13] 王洪华. 探地雷达二维无单元法正演模拟[D]. 长沙: 中南大学地球科学与信息物理学院, 2012: 1-54.

WANG Honghua. Two-dimensional element free method forward modeling for ground penetrating radar[D]. Changsha: Central South University. School of Geosciences and Info-Physics, 2012: 1-54.

[14] 李俊杰. 基于弱式无网格法的大地电磁二维正演[D]．长沙：中南大学地球科学与信息物理学院, 2014: 1-48.

LI Junjie. Magnetotelluric two-dimensional forward by weak-form meshfree methods[D]. Changsha: Central South University of Geosciences and Info-Physics, 2014: 1-48.

[15] 徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994: 229-235.

XU Shizhe. Finite element method for geophysics[M]. Beijing: Science Press, 1994: 229-235.

[16] ZHANG Lin, OUYANG Jie, WANG Xiaoxia, et al. Variational multiscale element-free Galerkin method for 2D Burgers equation[J].Journal of Computational Physics, 2010, 229(19/20): 7147-7161.

[17] ZHANG Zan, LI Dongming, CHENG Yumin. The improved element-free Galerkin method for three-dimensional wave equation[J]. Acta Mechanica Sinica, 2012, 28(3): 808-818.

[18] 焦玉玲, 刘金英, 杨天行, 等. 无网格法在地下水水位预测中的应用[J]. 吉林大学学报(地球科学版), 2007, 37(3): 535-540.

JIAO Yuling, LIU Jinying, YANG Tianxing, et al. Application of meshless method in groundwater level forecast[J]. Journal of Jilin University (Earth Science Edition), 2007, 37(3): 535-540.

[19] Cheng R J, Liew K M. A meshless analysis of three-dimensional transient heat conduction problems[J]. Engineering Analysis with Boundary Elements, 2012, 36(2): 203–210.

[20] REN Bo, LI Shaofan. Modeling and simulation of large-scale ductile fracture in plates and shells[J]. International Journal of Solids and Structures, 2012, 49(18): 2373-2393.

[21] Wang J G, Liu G R. A point interpolation meshless method based on radial basis functions[J]. International J Numer Meth Eng, 2002, 54(11): 1623-1648.

[22] Zhang X, Song K Z, Lu M W, et al. Meshless methods based on collocation with radial basis functions[J]. Comput Mechanics, 2000, 26(4): 333-343.

(编辑  陈灿华)

收稿日期：2013-10-12；修回日期：2013-12-24

基金项目(Foundation item)：国家自然科学基金资助项目(40874055)；湖南省自然科学基金资助项目(07JJ5065)(Project (40874055) supported by

National Natural Science Foundation of China; Project (07JJ5065) supported by Natural Science Foundation of Hunan Province of China)

通信作者：严家斌(1969-)，男，湖南常德人，副教授，从事电磁法数据处理及图像处理工作；电话：0731-88830906；E-mail：cspyry@csu.edu.cn

摘要：介绍无网格法的基本原理及二维大地电磁变分问题的无网格解法，对比3层介质模型相同数量节点下无网格法与有限元法计算精度的差异，研究支持域量纲为1的尺寸与高斯点数量对大地电磁场计算精度的影响，最后通过二维模型的计算进一步验证算法的有效性。研究结果表明：无网格法计算MT问题效果很好；在相同节点个数下无网格法精度比有限元法的精度高；支持域量纲为1的尺寸对其计算精度影响很大，较优值为1.0~1.2；高斯点数量对精度影响较小，2点高斯公式能满足精度要求。