基于上下文模型的混合傅里叶-小波图像降噪方法
邓宏贵,李明辉,高小龙
(中南大学 物理与电子学院,湖南 长沙,410083)
摘 要:
傅里叶变换去除图像噪声时各具不同的优点和不足,提出一种基于上下文模型的混合傅里叶-小波图像降噪方法。首先在傅里叶域中估计原始图像的功率谱密度,运用维纳滤波器降噪,降低原始图像噪声水平;再在小波域中通过基于上下文模型的自适应阈值法去除剩余噪声;在小波域中使用平稳小波变换分解图像信号得到分解后的系列小波系数,根据小波系数间的相关性,利用上下文模型求取小波系数的方差,将其代入由GGD模型估计出的阈值表达式得到自适应阈值,再用软阈值函数对小波系数进行处理,最后将处理后的小波系数进行小波逆变换完成去噪。仿真结果表明:该方法不仅能够有效滤除图像噪声,而且能够保留图像的边缘细节信号,抑制降噪引起的吉布斯现象。
关键词:
中图分类号:TN911.7 文献标志码:A 文章编号:1672-7207(2013)01-0166-06
Fourier-wavelet image reduction using context-based model
DENG Honggui, LI Minghui, GAO Xiaolong
(School of Physics and Electronic, Central South University, Changsha 410083, China)
Abstract: The strengths and weaknesses of Fourier transform and wavelet transform were discussed in the process of image-denoising. The image noise reduction methods were proposed using Fourier-wavelet transforms context-based model. The original image noise level was reduced by estimation of power spectral density of the original image in the Fourier domain and the use of Wiener filter. The remaining noise was removed by using adaptive wavelet threshold method based on context modeling. A series of wavelet coefficients were obtained by using the stationary wavelet transform to decompose the image signal. According to the correlation among those coefficients, the variance of wavelet coefficients was calculated by using the context model. The adaptive threshold was acquired by substituting the variance into the threshold expression estimated by the GGD model. Processing wavelet coefficients with soft thresholding function, the image denoise was completed by means of the wavelet inverse transform to wavelet coefficients. Simulation results show that the methods proposed can not only effectively filter out image noise, but also keep the edges of the image detail signal well and inhibit Gibbs phenomenon caused by noise reduction.
Key words: context model; Fourier-wavelet transform; image denoising
图像在获取和传输过程中常常会混入噪声,噪声的存在降低了图像分辨率,严重影响图像的后续处理[1-2]。为了改善图像质量,尽可能减少噪声对图像后续处理的影响,必须先对图像进行去噪。降噪过程既要尽可能去除图像所含噪声,同时保证在降噪过程中不损坏图像的细节信息[3]。傅里叶变换能有效地稀疏图像中有一定变化周期规律的纹理部分和变化平缓部分,但是,不能有效地表示图像中的突变部分[4]。小波变换能稀疏表示包含尖锐变化部分的信号如图像中的边,但不能有效表示图像中的纹理和缓慢变化部分[5-8]。上下文模型能够降低图像的熵(因为高阶熵小于零阶熵),在图像降噪和视频压缩中得到了广泛应用[9-11],因此,若能有一种降噪算法将上下文模型、傅里叶变换和小波变换融合起来,有可能获得比单独使用上下文模型、傅里叶变换或小波变换都要好的去噪效果。Grace等[6]提出一种简单的傅里叶-小波混合降噪方法,得到了较好的降噪效果,但其没有考虑小波系数之间的相关性。为此,本文作者在此基础上提出一种基于上下文模型的混合傅里叶-小波图像降噪方法,其步骤如下。
(1) 在傅里叶域中估计原始图像的功率谱密度,用维纳滤波器保守降噪,降低原始图像噪声的水平。
(2) 在小波域中去除剩余的噪声。将剩余含噪声的图像作平稳小波变换,得到含噪声图像的小波变换系数;将小波系数的阈值量化,对每一个小波分解系数,选择基于上下文模型的自适应阈值;使用软阈值函数对小波系数进行降噪处理,得到真实的图像小波系数估计;将修改后的小波系数作平稳小波逆变换,重建原始信号,最终获得降噪后的图像。
仿真结果表明:这种基于上下文模型的混合算法能有效的去除噪声,降噪后的图像质量比传统的小波降噪算法优,更便于图像的后续处理。
1 傅里叶域中的平稳降噪
设包含噪声的图像y模型为
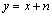 (1)
(1)
其中:x为原始图像;n为方差 的零均值高斯白噪声。傅里叶域中平稳逆滤波的频域响应为
的零均值高斯白噪声。傅里叶域中平稳逆滤波的频域响应为
 (2)
(2)
式中:Px(f)为信号x的功率谱密度;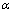 为调整参数。当
为调整参数。当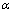 =1时,式(1)为维纳逆滤波器。用Y(f)表示含噪声信号y的傅里叶变换,对于每个数据点Y(f),在一个局部方形区域W(f)上,按下式计算功率谱密度Px(f)的估计
=1时,式(1)为维纳逆滤波器。用Y(f)表示含噪声信号y的傅里叶变换,对于每个数据点Y(f),在一个局部方形区域W(f)上,按下式计算功率谱密度Px(f)的估计 :
:
 ; s>0 (3)
; s>0 (3)
式中:M为方形窗口区域W(f)中傅里叶系数的个数;s为x的最小功率谱密度。用式(2)平稳逆滤波器对含噪声图像滤波,得:
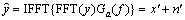 (4)
(4)
式中:FFT表示快速傅里叶变换;IFFT表示快速傅里叶逆变换;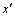 为被轻微扭曲的不含噪声的图像;
为被轻微扭曲的不含噪声的图像;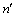 为剩余的噪声。下一步在小波域中去除剩余噪声。
为剩余的噪声。下一步在小波域中去除剩余噪声。
2 小波变换原理
小波变换是一种窗口大小固定、时间窗和频率窗都可以改变的时频局部化分析方法。设 ,L2(R)表示平方可积的实数空间,其傅里叶变换为
,L2(R)表示平方可积的实数空间,其傅里叶变换为 。当
。当 满足其相容性条件时,称
满足其相容性条件时,称 为1个基本小波或母小波。将母函数
为1个基本小波或母小波。将母函数 经过伸缩和平移后可以得到1个小波序列,对于任意函数
经过伸缩和平移后可以得到1个小波序列,对于任意函数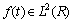 ,其连续小波变换为
,其连续小波变换为
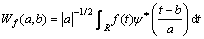 (5)
(5)
其中: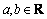 ;a为伸缩因子,a≠0;b为平移因子。其逆变换为
;a为伸缩因子,a≠0;b为平移因子。其逆变换为
 (6)
(6)
对于离散小波变换,令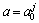 ,
,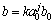 ,
, ,扩展步长
,扩展步长 ,为固定值,一般假定a0>1。对应的离散小波函数序列
,为固定值,一般假定a0>1。对应的离散小波函数序列 可表示为:
可表示为:
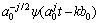 。若取a0=2,b0=1,则为二进小波变换。对于任意函数
。若取a0=2,b0=1,则为二进小波变换。对于任意函数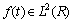 ,其离散小波变换为:
,其离散小波变换为:
 (7)
(7)
3 平稳小波变换的分解与重构
由于在图像信号的正交小波变换过程中,对分解的细节系数采取了门限阈值法去除噪声,易导致图像信号在奇异点产生吉布斯振荡。为了尽可能消除吉布斯现象,选用平稳小波变换算法对图像信号进行小波分解。平稳小波变换是一种冗余小波变换,具有平移不变性,因此,与正交小波变换相比,经过平稳小波变换后的图像在视觉上更加清晰、美观。
设正交小波高通滤波器的系数为Hi=(hi,1, …, hi,j,…, hi,J),低通滤波器的系数为Gi=(gi,1, …, gi,j,…, gi,J) (其中:i表示第i级滤波器;j表示第j个系数)。令Hi=ZiHi-1,Gi=ZiGi-1 (其中,Zi为插值补零算子),则
 ,
, (8)
(8)
当j不等于2i的整数倍时,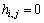 ,
,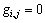 ,信号的平稳小波变换分解为:
,信号的平稳小波变换分解为:
 (9)
(9)
式(9)表明平稳小波变换过程中去除了下抽样处理,因此,每次平稳小波变换的逼近信号和细节信号的长度与原始信号的长度相同。
平稳小波逆变换过程如下:令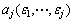 ,为对平稳小波变换逼近信号aj依次进行
,为对平稳小波变换逼近信号aj依次进行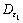 ,…,
,…,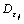 j次下抽样后的信号;
j次下抽样后的信号;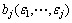 为对平稳小波变换细节信号bj依次进行
为对平稳小波变换细节信号bj依次进行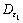 ,…,
,…,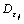 j次下抽样的信号,当
j次下抽样的信号,当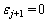 时,
时,
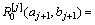
 (10)
(10)
当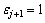 时,
时,
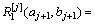
 (11)
(11)
式中:H*和G*分别为正交小波滤波器H和G的对偶算子。可以得出平稳小波变换的逆变换为:
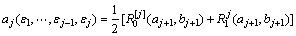 (12)
(12)
4 基于上下文模型的空间自适应阈值
使用平稳小波变换对含噪图像信号进行分解后得到一系列小波分解系数,采用软阈值对这些系数进行处理。软阈值降噪的方法是将小波系数与阈值进行比较,将大于或者等于阈值的系数在一定程度上缩小,反之就将系数置0。阈值的选取在阈值去噪法中非常重要:若阈值选得过小,则不能充分滤除图像的噪声;若阈值选得过大,则会导致过多的小波系数置0,在滤除噪声的同时也损失了图像的重要信息。由此可见:小波阈值降噪的关键是对阈值进行准确估计。本文采用基于广义高斯模型(GGD)的阈值估计法,小波系数矩阵用广义高斯分布进行建模。
广义高斯分布的概率密度函数为:
 ;
; <x<
<x< ,
,  >0 (13)
>0 (13)
式中:
 ;
;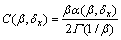 (14)
(14)
其中: 为标准方差;
为标准方差; 为广义高斯分布模型的形参。显然,当
为广义高斯分布模型的形参。显然,当 =2时,式(14)为高斯分布。Chang等[12]对基于广义高斯模型(GGD)的阈值进行了进一步研究,得到如下阈值表达式:
=2时,式(14)为高斯分布。Chang等[12]对基于广义高斯模型(GGD)的阈值进行了进一步研究,得到如下阈值表达式:
 (15)
(15)
式中: 为噪声方差;
为噪声方差;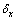 为标准方差。
为标准方差。
由此可见:阈值的估计在于如何估计噪声方差 和标准方差
和标准方差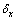 。对于
。对于 ,本文采用Donoho等[13]提出的鲁棒性中值法估计:
,本文采用Donoho等[13]提出的鲁棒性中值法估计:
 ;
;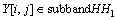 (16)
(16)
该方法不仅具有较好的鲁棒性,而且具有较高的计算精度,在小波降噪算法中得到广泛运用。由式(15)估计出噪声方差 后,只要求出标准方差
后,只要求出标准方差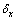 就能得到阈值。考虑到小波系数之间的相关性,本文采用基于上下模型的方法来估计标准方差
就能得到阈值。考虑到小波系数之间的相关性,本文采用基于上下模型的方法来估计标准方差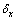 。
。
对于1个给定的系数,参数的估计以其邻域内系数的信息为条件,此方法称为上下文模型。上下文模型分为因果型和非因果型。因果型仅仅将其左边和上边的相邻元素作为有用信息,不能包含所有的样本信息;非因果型包含了上下左右所有相邻像素,因此,能够提供更加准确、有效的上下文信息。
下面用非因果型上下文模型估计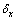 。用
。用 表示第k次小波分解的1个
表示第k次小波分解的1个 子带,用ui,j表示
子带,用ui,j表示 的周围系数。选取本层
的周围系数。选取本层 周围的8个小波系数和
周围的8个小波系数和 的双亲系数
的双亲系数 作为
作为 的周围小波系数,用P×1的向量ui,j表示。对于具体系数
的周围小波系数,用P×1的向量ui,j表示。对于具体系数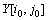 ,用
,用 表示其周围系数的上下文值,其值可以用周围小波系数的加权平均值来计算:
表示其周围系数的上下文值,其值可以用周围小波系数的加权平均值来计算:
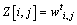 (17)
(17)
其中:w为权值。加权平均系数可由最小均方估计计算得到:
 (18)
(18)
式中:U为1个 阶矩阵,每一行为
阶矩阵,每一行为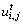 ;Y为包含子带上所有系数的
;Y为包含子带上所有系数的 向量,元素为
向量,元素为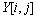 。由于平稳小波分解是冗余的,经过分解后的小波系数具有相关性,因此,邻域内系数之间加权平均值可以有效地表示平均信息。
。由于平稳小波分解是冗余的,经过分解后的小波系数具有相关性,因此,邻域内系数之间加权平均值可以有效地表示平均信息。
下一步根据Z[i, j]来分类Y[i, j],再根据每类Y[i, j]求取δ的参数估计,这就需要找出Z[i, j]和Y[i, j]之间的关系。研究表明[14]:取一段较小的z[i, j]区间,落在该区间内Y[i, j]的数量是较少的,而取一段较大的Z[i, j]的区间,落在该区间内Y[i, j]的数量也相应的较多,表明Z[i, j]区间和落在该区间Y[i, j]的数量成正比,由此可知上下文模型很好地体现了图像局部数据的变换性。对于某个特定的系数Y[i0, j0],在其相应的Z[i0, j0]上设置1个局部窗口,选择落在该窗口的上下文值系数{Y[i, j]},并对其求加权平均值,完成对Y[i0, j0]的方差估计。方法是取L个比Z[i0, j0]大且最靠近的点,L个比Z[i0, j0]小且最靠近的点,共有2L+1个相邻的点。在具体计算时,采用L=max(50, 0.02M2)进行计算。这样选取的目的是保证邻域内有足够多的系数,同时也能够保证以Z[i0, j0]为中心的窗口不会太大。边缘方差被估计如下:
 (19)
(19)
式中: 表示上下文值落在以Z[i, j]为中心的窗口内的系数集{Y[i, j]}中。将式(19)代入式(15),可求出点[i0, j0]处的阈值为:
表示上下文值落在以Z[i, j]为中心的窗口内的系数集{Y[i, j]}中。将式(19)代入式(15),可求出点[i0, j0]处的阈值为:
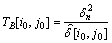 (20)
(20)
5 基于上下文模型的混合傅里叶- 小波去噪算法
基于上下文模型的混合傅里叶-小波降噪方法主要通过2步进行:首先,在傅里叶域中采用平稳逆滤波器保守去噪;然后,在小波域中采用基于上下文模型的自适应阈值法去除剩余噪声。 综上所述,本文图像降噪步骤如下。
(1) 在傅里叶域中估计原始图像的功率谱密度,用维纳滤波器进行保守降噪,降低原始图像的噪声 水平。
(2)在小波域中去除剩余噪声:
1) 将剩余含噪声的图像作平稳小波变换,得到含噪声图像的小波变换系数。
2) 小波系数的阈值量化。对每一个小波分解系数,选择基于上下文模型的自适应阈值
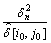 ;
;
3) 使用软阈值函数对小波系数进行降噪处理,得到图像的真实小波系数估计。
4) 将修改后的小波系数作平稳小波逆变换,重建原始信号,最终获得降噪后的图像。降噪流程见图1。
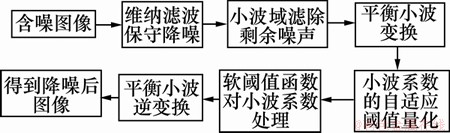
图1 降噪流程示意图
Fig.1 Flow diagram of denoising
6 仿真结果和分析
本文的实验硬件环境如下:CPU为Genuine Intel(R)1.73 GHz,内存为1 G的微机,软件环境为matalb7.9b。仿真所采用的Cameraman,House和Rice 3幅图像均来自标准测试图像库。实验过程中选择的小波域和傅里叶域中窗口尺寸分别是3×3和7×7, ,小波变换选用Haar小波进行3层分解。具体过程如下:对加有零均值高斯白噪声的上述3幅图像Cameraman,House和Rice分别采用如下方法进行降噪:文献[2]提出的混合傅里叶小波降噪法;Grace等[6]提出的基于上下文模型的降噪法;Donoho等[8]提出的经典硬阈值法;本文提出的基于上下模型的混合傅里叶小波图像降噪方法。当噪声方差不同时,使用峰值信噪比(PSNR)来检验降噪效果。表1和表2所示分别为噪声方差不同时,采用以上方法对Cameraman和House图像降噪后所得到的峰值信噪比(即PSNR)。图2所示为图像Cameraman,Rice和House图像在
,小波变换选用Haar小波进行3层分解。具体过程如下:对加有零均值高斯白噪声的上述3幅图像Cameraman,House和Rice分别采用如下方法进行降噪:文献[2]提出的混合傅里叶小波降噪法;Grace等[6]提出的基于上下文模型的降噪法;Donoho等[8]提出的经典硬阈值法;本文提出的基于上下模型的混合傅里叶小波图像降噪方法。当噪声方差不同时,使用峰值信噪比(PSNR)来检验降噪效果。表1和表2所示分别为噪声方差不同时,采用以上方法对Cameraman和House图像降噪后所得到的峰值信噪比(即PSNR)。图2所示为图像Cameraman,Rice和House图像在 的含噪图像,图3所示为本文方法降噪后的Cameraman,House和Rice图像。
的含噪图像,图3所示为本文方法降噪后的Cameraman,House和Rice图像。
表1 各方法降噪后Cameraman图像PSNR的比较
Table 1 Performance comparison of Cameraman for denoising methods in terms of PSNR dB

表2 各方法降噪后House图像PSNR的比较
Table 2 Performance comparison of House for denoising methods in terms of PSNR dB


图2 δn=20时实验采用的含噪图像
Fig.2 Noisy images for experiments when δn=20

图3 本文方法降噪后的图像
Fig.3 Simulation results from experiment using proposed method in the paper
从表1和表2可知:无论是Camerman图像还是House图像,采用本文方法所得峰值信噪比与其他方法相比均有较大提高;对于House图像,当δn=20时,本文方法的信噪比与文献[6]中的方法相比提高了0.6 dB,比文献[2]中的方法提高了近1.7 dB,这表明本文方法的有效性和优越性。从仿真图像的视觉效果看:本文方法利用了傅里叶域与小波变换对信号的有效表示,在去除了图像噪声的同时,很好地保留了图像的边缘细节信号,并有效抑制了降噪后常出现的吉布斯现象。
7 结论
(1) 利用上下文模型对小波系数进行分类,根据小波系数层内与层间的相关性,得到小波系数的上下文值,对其加权平均,求取其上下文矩阵,最后获得阈值矩阵,得到的阈值具有较强的空间自适应性。
(2) 平稳小波变换去除了下抽样处理,保留了更多的小波系数信息,分解的系数是相关的,故邻域内系数的加权平均值能有效地表示平均信息。利用该特点,结合上下文模型求各个尺度的空间自适应阈值,大大减少了计算复杂度,缩短了程序的计算机耗时。
(3) 本文使用的是二维可分离的离散平稳小波变换,若能将不可分离的离散小波变换如Contourletd运用在混合傅里叶-小波图像降噪算法中,将能够进一步提高降噪效果。
参考文献:
[1] Shi F, Selesnick I W. An elliptically contoured exponential mixture model for wavelet based image denoising[J]. Applied and Computational Harmonic Analysis, 2007, 23(1): 131-151.
[2] 郭强, 郁松年. 基于三变量模型的剪切波降噪方法[J]. 自动化学报, 2010, 36(8): 162-172.
GUO Qiang, YU Songnian. Shear wave denoising based on three-variable model[J]. Journal of Automation, 2010, 36(8): 162-172.
[3] 袁修贵, 王军, 黄修建, 等. 基于小波变换的一种图像增强算法[J]. 中南大学学报: 自然科学版, 2005, 36(2): 298-301.
YUAN Xiugui, WANG Jun, HUANG Xiujian, et al. An image enhancement denoising on wavelet transform[J]. Journal of Central South University: Science and Technology, 2005, 36(2): 298-301.
[4] 王远干, 喻洪麟, 朱传新. M周期分数傅里叶变换的光栅信号去噪方法[J]. 光电工程, 2006, 33(7): 110-114.
WANG Yuangan, YU Honglin, ZHU Chuanxin. M-cycle fractional Fourier transform of the grating signal denoising[J]. Electro-Optical Engineering, 2006, 33(7): 110-114.
[5] Mahbubur S M, Rahman M. Omair A. Improved restoration using wavelet-based denoising and fourier-based deconvolution[J]. Image Processing, 2008, 4(2): 249-251.
[6] Grace S, Martin V. Spatially adaptive wavelet thresholding with context modeling for image denoising[J]. Image Processing, 2000, 9(9): 1522-1531.
[7] Wang H X, Robert S H. Microarry image enhancement by denoising using stationary wavelet transform[J]. Transactions on Nanobioscience, 2003, 2(4): 184-188.
[8] Donoho D L, Johnston I M. Ideal spatial adaptation by wavelet shrinkage[J]. IEEE Transactions on Image Processing, 1994, 81(3): 425-455.
[9] Chang S, Yu B, Vetterli M. Spatially adaptive wavelet thresholding with context modeling for image denoising[J]. IEEE Transactions on Image Processing, 2000, 9(9): 1522-1531.
[10] 董世都, 杨小帆, 黄同愿. 一种基于三维小波系数上下文模型的视频压缩方法[J]. 小型微型计算机系统, 2005,26(11): 2021-2024.
DONG Shidu, YANG Xiaofan, HUANG Tongyuan. An video compression method based on the context model of three-dimensional wavelet coefficients[J]. Journal of Chinese Computer Systems, 2005, 26(11): 2021-2024.
[11] GUANG Taozhai, WU Xiaolin, YAO Xiaokang. MDL context modeling of images with application to denoising[J]. IEEE Trans Image Process, 2009, 9(7): 3845-3848.
[12] Chang S G, Yu B, Martin V. Adaptive wavelet thresholding for image denoising and compression[J]. IEEE Transactions on Image Processing, 2000, 9(9): 1532-1546.
[13] Donoho D L, Johnstone I M. Adapting to unknown smoothness via wavelet shrinkage[J]. Journal of the American Statistical Assoc, 1995, 90(12): 1200-1224.
[14] Donovan G, Geronimo J S, Hardin D, et al. Construction of orthogonal wavelets using fractal interpolation functional[J]. SIAM J Math Anal, 1996, 27: 1158-1192.
(编辑 陈灿华)
收稿日期:2011-11-25;修回日期:2012-03-10
基金项目:国家自然科学基金资助项目(61071025);中南大学学位论文创新基金资助项目(2010ssxt012)
通信作者:邓宏贵(1965-),男,湖南武冈人,博士,教授,从事智能优化算法、图像处理、无线传感器网络研究;电话:0731-88836443;E-mail: denghonggui@163.com
摘要:针对小波变换和傅里叶变换去除图像噪声时各具不同的优点和不足,提出一种基于上下文模型的混合傅里叶-小波图像降噪方法。首先在傅里叶域中估计原始图像的功率谱密度,运用维纳滤波器降噪,降低原始图像噪声水平;再在小波域中通过基于上下文模型的自适应阈值法去除剩余噪声;在小波域中使用平稳小波变换分解图像信号得到分解后的系列小波系数,根据小波系数间的相关性,利用上下文模型求取小波系数的方差,将其代入由GGD模型估计出的阈值表达式得到自适应阈值,再用软阈值函数对小波系数进行处理,最后将处理后的小波系数进行小波逆变换完成去噪。仿真结果表明:该方法不仅能够有效滤除图像噪声,而且能够保留图像的边缘细节信号,抑制降噪引起的吉布斯现象。


