基于有限元-无限元耦合的2.5D直流电阻率数值模拟-有色金属在线

限元截断边界所引起的问题，提出一种新的2.5D直流电阻率有限元-无限元耦合数值模拟方法。首先推导无限元2.5D单元映射函数，然后提出一种无限元形函数，将其与传统有限元相结合，取代传统的混合边界，使得电位在无限域内连续并在无限远处衰减为0 V，最终形成的刚度矩阵稀疏对称并与场源位置无关。研究结果表明：在相同的网格剖分下，有限元无限元耦合方法比传统有限元法能够在边界测点处得到更高的计算精度，能够在较小的计算范围内得到更优的计算结果，从而有利于减少节点数，提高计算速度；由于系数矩阵不随场源位置改变，有利于加速反演计算。

关键词：

2.5D；有限元-无限元；数值模拟；电法勘探；

中图分类号：P631.3 文献标志码：A 文章编号：1672-7207(2014)08-2691-10

2.5-D DC resistivity forward modeling by finite-infinite element coupling method

XIAO Xiao, YUAN Yuan, TANG Jingtian

(Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education,

School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)

Abstract: To solve the problems caused by artificial boundary conditions in conventional finite element modeling, a new 2.5D DC resistivity finite-infinite coupling method was proposed. Firstly, the 2.5D mapping functions of infinite elements were derived. Then, a new type of shape functions was proposed. Infinite element method was integrated into conventional finite element method to replace the mixed boundary conditions, which made the electrical potential distribute continuously in half space and decay to 0 at infinity. Meanwhile, the global system matrix was independent of the locations of source points but still sparse and symmetric. The results show that the finite-infinite coupling method can obtain a more accurate solution than traditional FEM method in the same meshing area, and reasonable numerical solutions can be obtained in a relatively small meshing area. Due to the reduction of the discretization domain and node, it can improve the calculation speed. A more superior property is the invariability of the global system matrix with variant source positions which makes this new method alleviate the computational burden and speed up inversions.

Key words: 2.5D; finite-infinite; numerical simulation; electric prospecting

有限单元法以其灵活地模拟任意复杂模型而广泛应用于地球物理正演模拟中。但该方法的正演速度在很大程度上依赖于网格节点数，而快速的正演模拟是反演的基础，因此，如何减少网格节点数，在较小的计算范围内得到高精度的正演结果具有重要意义。对于稳定电流场数值模拟，目前广泛使用的边界条件有2类：第一类是混合边界条件，它能够在合理的范围内得到较高的正演精度，但是，刚度矩阵与点源位置有关，因此，每移动1次点源位置就需要重新计算刚度矩阵和求解方程组，这对于需要多次移动电源的剖面测量方法如对称四极、偶极-偶极等装置，1条断面的测量将涉及数十次电源移动，其正演模拟需要较长时间，而反演更耗时；第二类是用齐次边界条件包括Neumann 边界条件^[1]和Dirichlet边界条件^[2-3]，即在半无限边界上强制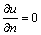或u=0(其中，u为电位，n为边界外法向单位矢量)；或者认为边界积分函数中为常数，提至积分号以外而不考虑其变化^[4-5]。采用齐次边界条件必须将计算范围加大，从而减少边界对计算结果的影响，这必将增加网格节点数，从而增加计算量。为克服这2类边界条件的不足，本文作者在传统有限元数值模拟的基础上引入无限单元法(infinite element method)，既保证刚度矩阵与点源位置不再相关，而且在较小的网格划分范围内即可满足精度要求，从而极大地提高了计算效率。目前，无限元大体可分为Bettess映射无限元^[6-7]、Astley波包映射无限元(mapped wave envelope elements)^[8-9]和Burnett多极展开(multipole expansion)无限元^[10-11]，其中Astley波包映射无限元应用最广泛。其基本思想是坐标变换和位场采用不同的插值函数，通过坐标映射实现无限域积分，并在映射后的局部坐标里建立位场插值形函数，使位场在有限元网格和无限元网格结合处保持一致性，而在无限远处衰减为0^[12]。无限元目前已较多地应用于声学、电磁学、岩土力学等领域^[13-17]。在地球物理领域，Fu等^[18]在弹性波方面应用了无限元来处理吸收边界条件； Blome等^[19]应用Astley无限元处理直流电法边界问题，缩小了计算范围，减少了节点数, 并且避免了采用Dirichlet或混合边界条件。汤井田等^[20]对Blome的工作进行了研究，发现其采用的无限元形函数较复杂，且由于引入了Astley无限元中特有的额外权重因子，使整体系数矩阵失去了对称性，此外，该种无限元会在某些情况下导致线性方程组不收敛。张玉娥等^[21]用无限元研究地铁区间隧道地震反应分析；姜忻良等^[22]用其研究交叉隧道地震反映；朱军等^[23]在三维电测井中成功应用无限元来提高计算速度；孙跃^[3]提出了将有限元、无限元相结合来计算三维稳定电流场的方法，效果优于Dirichlet边界条件，但仅给出了基于六面体单元的基本公式和简单结果，对无限元映射函数和形函数均未进行详细说明。目前，有限元无限元耦合技术在2.5D问题中的应用仍为空白。本文作者将有限元-无限元耦合技术应用于2.5D直流电阻率问题中。首先从2.5D点源电场边值问题出发，利用Galerkin方法简单推导有限元基本公式。随后推导二维情况下的无限元坐标映射函数，将一种无限元形函数应用于本文的有限元-无限元耦合方法中。最后，通过一系列数值模拟证明本算法在保证计算精度的同时能够大大提高计算效率，有利于快速反演。

1 有限元法基本方程

1.1 2.5D点源场边值问题

假设地下电性分布沿y方向不变，点源位于地表时的2.5D稳定电流场边值问题可表示为^[24]：

(1)

其中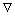：为二维哈密顿算子，；k为波数；U为三维空间中的电位u沿y方向进行傅氏变换后的波数域电势；K₀(kr)和K₁(kr)分别为零阶和一阶第一类修正Bessel函数；l_s和l_∞分别为地表和地下边界；r为点源到外边界任意点的距离。

通过对U进行反傅里叶变换后，即得空间中任意一点的电位u(x，y，0)：

(2)

1.2 有限单元法

采用矩形单元和双线性插值，根据Galerkin加权余量法推导与式(1)对应的变分问题，令

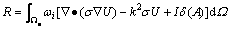(3)

其中：为权函数，在Galerkin法中一般取权函数为形函数N_i(i=1，…，4)。根据Green定理，有

(4)

其中：n为边界l_∞的外法向单位矢量。令R=0，得

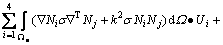
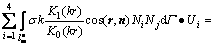
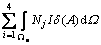(5)

对式(5)进行单元积分，并将所有单元积分根据节点相加，得总体线性代数方程组：

(6)

解方程组，即可得到各节点上的点位U，然后，通过反傅氏变换即可得到二维半空间中的电位。

2 无限元与有限元结合

2.1 无限元几何映射

本文所采用的无限元为Astley无限单元^[8-9^,^13-14]。在有限元网格边界外增加无限单元，通过坐标映射将单元在某一方向扩展到无限元处的积分，此时无需再考虑边界条件。采用有限元-无限元耦合方法与有限元法唯一的不同即在于对边界的单元分析。在有限元-无限元中，边界处的无限元的坐标变换和位场插值需采用不同的插值函数，分别称为映射函数(mapping function)和形函数(shape function)。一维情况下的映射函数如图1所示。

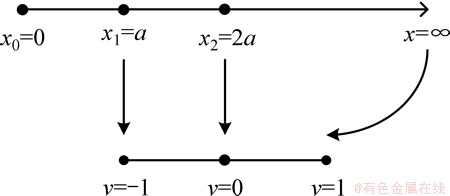
图1 一维无限元映射

Fig. 1 1D infinite element mapping

如图1所示，整体坐标下的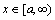被映射到局部坐标下的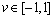有限范围内，映射关系为

(7)

其中：M₁(v)和M₂(v)为映射函数，

(8)

这种映射具备唯一性，并且在二维和三维情况下均适用。由式(7)和(8)可以得到

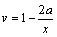(9)

式(9)表明v呈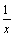型衰减。对于电位形函数，设v为-1，0和1处的电位分别为u₁，u₂和u₃，假使采用传统有限元二次插值形函数，即

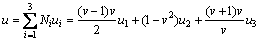(10)

将式(9)代入式(10)，并考虑到无限远处u₃=0，得

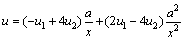(11)

式(11)表明u呈型衰减，符合点电源在无限半空间中衰减的物理规律，因此，将此种映射应用于点源直流电法问题具有合理性。

将上述映射推广到二维情况，采用基于矩形的有限单元和无限单元网格，无限单元映射示意图如图2所示。

图2 二维无限元映射

Fig. 2 2D infinite element mapping

映射原点P为所有无限单元的映射出发点，一般可取在上表面的中点处。以P点为原点，经过有限单元在外边界上的矩形单元的2个顶点，向外引出2条射线，形成无限单元的几何形式。点P到点3和点4的距离分别为点P到点1和点2距离的2倍。在无限远处还有2个无限单元节点，它们使得势场分布扩展到无限远处。但是，由于无限远处电位为0 V，因此，这2点不参与插值运算，也没有必要予以考虑。在局部坐标中，无限单元被映射为1个有限大小的矩形，从而可进行积分运算，其中，ξ方向表示无限远方向，其映射方式与一维无限单元映射方式相同，电位插值则采用特殊的形函数。由于2维问题的电性分布沿y方向不变，因此不予考虑。对于z方向的无限单元映射和插值函数，采用与有限单元相同的映射形式和形函数。

坐标映射为

(12)

其中：L_i为长度坐标。结合图2，有

(13)

再结合ξ方向的坐标映射关系式(7)，得到四节点无限单元的节点坐标映射函数

(14)

其中：i=1，2；

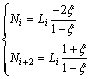(15)

经过上述坐标映射后，电位借助于无限单元延伸至无限远处，并且在无限远处衰减为0 V。此时，无需再考虑边界条件，即计算时无需考虑边界积分。无限单元的单元分析与有限元单元分析相类似，只是矩形单元变为了四节点无限元单元。

2.2 无限元形函数

沿η方向，电位形函数与坐标映射函数相同，见式(13)。在图2中的ξ方向，无限单元采用特殊的电位插值形函数。该方向上形函数的选择一直是研究热点，只有根据不同的场源性质选择合适的形函数才能达到较好的效果。

汤井田等^[20]对多种无限元形函数的计算精度和计算时间进行了对比，包括国内岩土力学领域常用的传统有限元二次Lagrange插值函数、改进型二次Lagrange插值函数、考虑额外加权因子的改进型二次Lagrange插值函数等，最终提出一种适用于稳定电流场问题的形函数。该函数无论在计算速度还是精度上均具有优势，因此，本文2.5D直流电阻率也采用该形函数。

该形函数是在传统二次Lagrange插值函数前乘以修正系数，再组合单元矩阵，这样得到的系数矩阵依然为对称矩阵。此时，无限单元电位插值形函数为

(16)

其中：i=1，2。

3 算例及分析

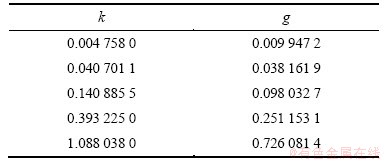
为了验证有限元-无限元耦合法在2.5D稳定电流场中应用的可靠性，对多种地电模型进行计算。程序中均采用变带宽存储方式将刚度矩阵集成在一维数组中，然后采用对称变带宽线性方程组求解程序^[25]进行求解。所有计算均在CPU 3.0 Ghz和4G RAM的个人计算机上完成。模型计算中采用的波数见表1。

表1 模型计算所用的波数k及加权系数g

Table 1 Wave number and weighted coefficient used in numerical calculations

3.1 水平2层模型

针对2层介质模型，对传统的混合边界条件、齐次边界条件以及无限元边界条件的计算结果与解析解、自适应有限元解^[26-30]以及二次场解进行对比。水平2层介质模型示意图模型如图3所示，上层电阻率为100 Ω·m，层厚为10 m，下层电阻率为10 Ω·m。采用固定点源的二极装置进行测量，供电电极A位于(0,0)处，测量电极M从(0,1)到(0，100)，x表示AM之间的距离。网格剖分区域为600×300。

图3 水平2层介质模型示意图

Fig. 3 Two layered model

采用混合(mixed)边界条件、齐次(Dirichlet)边界条件以及无限元(infinite)边界条件计算的视电阻率曲线如图4所示，同时，将各种边界的计算结果与自适应有限元及二次场计算结果进行对比。

从图4可看出：对于测区[0,20]，5条数值计算结果的曲线均与解析解拟合很好，而随着测点M逐渐靠近计算区域的边界，由有限元-无限元耦合的计算结果与解析解依然拟合较好，而由混合边界条件及齐次边界条件下的传统有限元方法所得结果则产生了较大的误差。本模型算例中，除了自适应有限元算法外，其余算法均采用相同的网格剖分、相同的方程组求解方法、相同的计算精度以及运行环境，因而其计算误差的差异完全是由所采用的边界条件产生；有限元-无限元耦合的结果与解析解拟合较好，正是由于本文程序所采用的无限元边界条件使得电位在边界处趋于0，从而避免了截断误差。数值结果表明有限元-无限元耦合方法在边界处能够得到较高的精度，同时也说明在相同的精度下，有限元-无限元耦合与传统有限元相比能够在相对更小的计算范围内达到精度要求，因此，节点数也会减少，从而提高正演模拟速度。

图4 不同方法求得的水平2层介质视电阻率曲线

Fig. 4 Apparent resistivity curves of two layered model with different boundary conditions

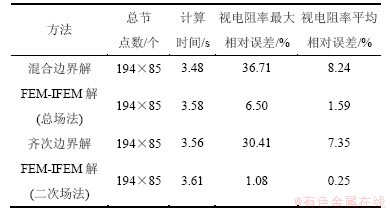
从图4可看出：传统有限元结果随着测点逐渐靠近边界，误差也逐渐增大，混合边界条件的有限元结果在边界处(x=100)产生最大误差36.71%，齐次边界条件的有限元在边界处产生最大误差30.41%；有限元-无限元耦合方法(总场法)在边界附近的误差得到较好控制，在边界处的误差仅为0.53%，整个边界附近的误差也都保证在2.7%以内，大大改善了边界处的计算结果。将有限元-无限元耦合法应用于二次场法中，其计算结果甚至优于自适应有限元法计算结果，二者在所有测点中的最大误差分别为1.08%和2.31%。

不同方法计算效率及误差对比如表2所示。从表2可以看出：2种传统有限元方法与2种有限元-无限元耦合方法采用相同的网格剖分，总节点数为16 490，因此，四者的计算速度也相差很小，但有限元-无限元耦合可得到更高的精度，尤其对于二次场法，边界处的最大相对误差为1.08%，平均相对误差为0.25%。

表2 不同方法计算效率及误差对比

Table 2 Comparison about efficiency and relative error of different methods

3.2 均匀半空间中赋存圆柱体

为进一步说明有限元无限元耦合方法的计算效率，对均匀半空间中赋存圆柱体模型进行计算。均匀半空间赋存圆柱体模型示意图如图5所示，圆柱体电阻率为1 Ω·m，背景电阻率为100 Ω·m，圆柱体顶埋深为1 m，半径为1 m。采用偶极-偶极装置进行测量，偶极距==1 m，隔离系数n为1~8。

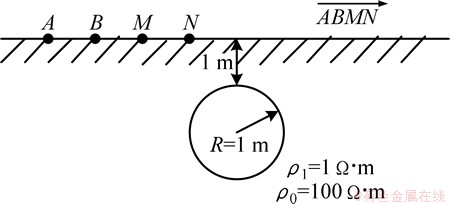
图5 均匀半空间赋存圆柱体模型示意图

Fig. 5 Infinite horizontal cylinder buried in half space

图6所示为有限元-无限元耦合法与传统混合边界条件计算的视电阻率断面图。网格剖分范围分别为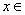[-256,256],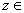[0,256]，测量区域均为[-10,10]。从图6可看出：混合边界、齐次边界条件下的传统有限元结果和有限元-无限元耦合结果均能很好地反映出异常，然而，混合边界下FEM的计算效率与另2种方法有很大差别。以n=1时的第1条剖面(8个测点)计算为例，采用混合边界条件的有限元方法计算时间为325.89 s，而相同网格剖分(总单元节点数为31 222)及计算环境下，由于有限元-无限元耦合方法及齐次边界下的FEM法的系数矩阵与点源位置无关，系数矩阵仅进行1次分解，然后，不断回代即可求得电位和视电阻率，其计算时间分别为27.13 s和27.02 s，效率提高了10余倍；随着测点数的增加，采用混合边界条件的计算时间也大大增加，而有限元-无限元耦合方法只是增加求解方程组时的回代次数，不会便时间增加太多。

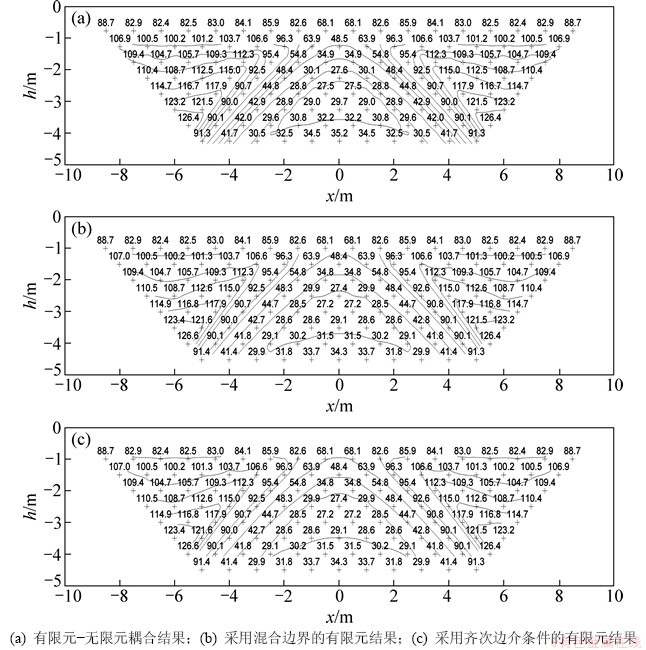
图6 大网格剖分区域下的视电阻率断面图(偶极-偶极装置)(视电阻率单位：Ω·m)

Fig. 6 Section of apparent resistivity with big mesh area (dipole-dipole configuration)

在证明有限元-无限元方法的有效性后，将计算区域减小，进一步验证有限元-无限元方法的优劣。图7所示为小区域下不同方法计算的视电阻率断面图，网格剖分范围分别为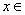[-14,14],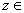[0,14]。测量区域均为[-10,10]，总单元节点数为29 250。对模型计算8条剖面，总测点数为116。黄俊革等^[1]对齐次边界条件下电阻率有限元进行了分析，得出边界距离应为100~150 m，而本模型中边界距离仅为14 m。从图7可看出：在小区域下，虽然不同方法依然能够反映出异常体，但不同方法计算的视电阻率明显不同。

表3所示为不同方法计算的视电阻率速度及精度对比结果。从整个断面的计算时间看，大区域的求解时间均多于小区域的求解时间；而对于相同的测量区域，混合边界条件下的FEM计算时间远远多于齐次边界及无限元边界的计算时间；对不同网格剖分区域及不同求解方法的结果均与大区域下混合边界条件解进行对比，发现在大区域下，即使齐次边界条件也可得到较高精度的计算结果；而在小网格剖分区域下，齐次边界解的最大相对误差为17.04%，平均相对误差为5.63%；混合边界解的最大相对误差为9.54%，平均相对误差为1.63%；本文无限元边界解最优，最大相对误差为7.52%，平均相对误差为1.60%，可见本文提出的有限元-无限元耦合算法，不仅能够得到优于传统混合边界条件的高精度计算结果，而且能够大大提高计算速度，再次证明本文方法的优越性。

3.3 有限元-无限元耦合法与边界元法对比

均匀半空间中赋存的3个块状异常体模型如图8所示。Xu等^[31]采用该模型计算了电位。本文对相同模型采用有限元-无限元耦合法进行计算，并对不同边界的数值解进行对比。如图8所示，3个异常体的电阻率分别为0.1，10.0和50.0 Ω·m，均匀半空间电阻率为1 Ω·m。整个异常体的边长为1 m，顶埋深为1 m。采用二极AM装置进行测量，点源A位于(0,0)处且固定不动。测点M从-10 m 到10 m移动，电极间距为2 m。

图7 小网格剖分区域下的视电阻率断面图(偶极-偶极装置)(视电阻率单位：Ω·m)

Fig. 7 Section of apparent resistivity with small mesh area (dipole-dipole configuration)

表3 不同方法计算的视电阻率误差对比

Table 3 Relative error of apparent resistivity with different boundary conditions

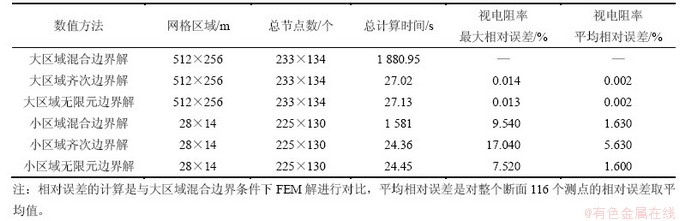
表4所示为采用边界元法 (BEM)、有限元法(FEM)、有限元-无限元耦合法以及传统有限元法(包括混合边界条件和齐次边界条件)得到的计算结果。与边界元法相比，在混合边界条件和齐次边界条件下的传统有限元和有限元-无限元耦合法计算的最大相对误差分别为4.20%，3.63%和2.95%，平均相对误差分别为2.05%，3.03%和1.40%(总测点数为10)，说明有限元-无限元耦合法的计算精度比传统有限元法的高。

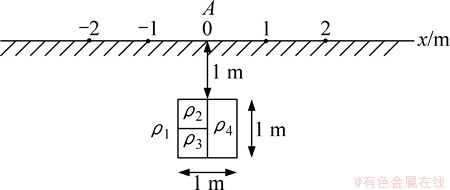
图8 均匀半空间中赋存3个块状异常体

Fig. 8 Three blocks buried in homogeneous half space

表4 不同方法计算的电位对比(点源A=0)

Table 4 A comparison of potential calculated with different methods

3.4 地质体模型

图9所示为多个地质体赋存的较复杂模型，背景电阻率为100 ·m，低阻体长×宽为4 m×4 m，电阻率为5 Ω·m，高阻体长×宽为3 m×3 m，电阻率为500 Ω·m。采用偶极偶极装置进行测量，取==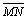2 m，隔离系数n取1~5，网格剖分区域为80 m×40 m。

图9 均匀半空间中赋存2个矩形异常体模型示意图

Fig. 9 Two rectangular prisms buried in half space

图10所示为偶极-偶极装置下的视电阻率断面图。计算采用较小的网格剖分区域为80×40。从图10可看出：在较小的剖分区域下，混合边界下的传统有限元与有限元-无限元耦合方法计算结果相差很小，再次证明本文提出的有限元无限元耦合方法能够满足精度需求。

图10 均匀半空间中赋存2个矩形异常体视电阻率断面图(视电阻率单位：Ω·m)

Fig. 10 Section of apparent resistivity for two rectangular prisms buried model

4 结论

(1) 在相同测区的计算范围内，有限元-无限元耦合方法与传统的混合边界条件或齐次边界相比能得到更高的计算精度，尤其是当测点距离边界较近时，传统有限元方法相对而言误差较大，有限元-无限元耦合方法依然能够保证5%以内的相对误差。

(2) 将有限元无限元耦合法应用于二次场后，其计算精度甚至与自适应有限元法的计算精度相近，不仅点源附近测点的误差更小，而且整个测线的平均相对误差也更低。

(3) 传统的有限元方法因采用截断边界条件需要较大的网格范围，而有限元-无限元耦合法只需与计算区域相当的网格剖分范围就可满足精度要求，提高了计算效率。

(4) 在保证精度的前提下，由于无限元边界与点源位置无关，因而，对于移动点源的剖面测量，本文方法可大幅提高计算效率，为快速反演提供了改进的途径。

参考文献：

[1] 黄俊革, 阮百尧, 鲍光淑. 齐次边界条件下三维地电断面电阻率有限元数值模拟法[J]. 桂林工学院学报, 2002, 22(1): 11-14.

HUANG Junge, RUAN Baiyao, BAO Guangshu. FEM under quantic-boundary condition for modeling resistivity on 3D geoelectric section[J]. Journal of Guilin Institute of Technology, 2002, 22(1): 11-14.

[2] Zhao S K, Yedlin M J. Some refinements on the finite-difference method for 3D DC resistivity modeling[J]. Geophysics, 1996, 61(5): 1301-1307.

[3] 孙跃. 直流电阻率法的三维有限元无限元数值分析[J]. 岩土工程学报, 2005, 27(7): 733-737.

SUN Yue. Numerical analysis for three-dimensional resistivity model by using finite element/infinite element methods[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(7): 733-737.

[4] 阮百尧, 熊彬, 徐世浙. 三维地电断面电阻率测深有限元数值模拟[J]. 地球科学D, 2001, 26(1): 73-77.

RUAN Baiyao, XIONG Bin, XU Shizhe. Finite element method for modeling resistivity sounding on 3D geoelectric section[J]. Earth Science D, 2001, 26(1): 73-77.

[5] 强建科, 罗延钟. 三维地形直流电阻率有限元法模拟[J]. 地球物理学报, 2007, 50(5): 1606-1613.

QIANG Jianke, LUO Yanzhong. The resistivity FEM numerical modeling on 3D undulating topography[J]. Chinese Journal of Geophys, 2007, 50(5): 1606-1613.

[6] Zienkiewicz O C, Bettess P. Diffraction and refraction of surface wave using finite and infinite elements[J]. International Journal For Numerical Methods in Engineering, 1977, 13(11): 1271-1290.

[7] Astley R J, Bettess P, Clark P J. Mapped infinite elements for exterior wave problems[J]. International Journal For Numerical Methods in Engineering, 1991, 32(1): 207-209.

[8] Astley R J, Macaulay G J. Mapped wave envelope elements for acoustical radiation and scattering[J]. Journal of Vibration and Acoustics, 1994, 170(1): 97-118.

[9] Astley R J, Macaulay G J, Coyette J P, et al. Three-dimensional wave-envelope elements of variable order for acoustic radiation and scattering. Part I. formulation in the frequency domain[J]. The Journal of the Acoustical Society of America, 1998, 103(1): 49-63.

[10] Burnett D S. A three-dimensional acoustic infinite element based on a prolate spheroidal multipole expansion[J]. The Journal of the Acoustical Society of America, 1994, 96(5): 2798-2816.

[11] Burnett D S, Holford R L. Prolate and oblate spheroidal acoustic infinite elements[J]. Computer Methods in Applied Mechanics and Engineering, 1998, 158(1): 117-141.

[12] 史贵才. 脆塑性岩石破坏后区力学特性的面向对象有限元与无界元耦合模拟研究[D]. 武汉: 中国科学武汉院岩土力学研究所, 2005: 1-25.

SHI Guicai. Research on post-failure mechanical properties of brittle-plastic rocks by OOFEM coupled with IEM[D]. Wuhan: The Chinese Academy of Sciences. Wuhan Institute of Rock and Soil Mechanics, 2005: 1-25.

[13] 李录贤, 国松直, 王爱琴. 无限元方法及其应用[J]. 力学进展, 2007, 37(2): 161-174.

LI Luxian, GUO Songzhi, WANG Aiqin. The infinite element method and its application[J]. Advances in Mechanics, 2007, 37(2): 161-174.

[14] Li L X, Sun J S, Sakamoto H. A generalized infinite element for acoustic radiation[J]. Journal of Vibration and Acoustics, 2005, 127(1): 2-11.

[15] 应隆安. 无限元方法[M]. 北京: 北京大学出版社, 1992: 162-172.

YING Longan. The infinite element method[M]. Beijing: Peking University Press, 1992: 162-172..

[16] 燕柳斌. 结构分析的有限元及无限元法[M]. 武汉: 武汉工业大学出版社, 1998: 1-104.

YAN Liubing. Finite element and infinite element methods for structure analysis[M]. Wuhan: Wuhan University of Technology Press, 1998: 1-104.

[17] 汪金山, 李朗如. 二维稳态电磁场数值计算中的无限元方法[J]. 电工技术学报, 1996, 11(3): 56-59.

WANG Jinshan, LI Langru. Infinite element method of computation of 2D stationary electromagnetic field[J]. Transactions of China Electrotechnical Society, 1996, 11(3): 56-59.

[18] Fu L Y, Wu R S. Infinite boundary element absorbing boundary for wave propagation simulations[J]. Geophysics, 2000, 52(2): 596-602.

[19] Blome M, Maurer H R, Schmidt K. Advances in three-dimensional geoelectric forward solver techniques[J]. Geophys J Int, 2009, 176(3): 740-752.

[20] 汤井田, 公劲喆. 三维直流电阻率有限元-无限元耦合数值模拟[J]. 地球物理学报, 2010, 53(3): 717-728.

TANG Jingtian, GONG Jinzhe. 3D DC resistivity modeling by finite-infinite element coupling method[J]. Chinese Journal of Geophysics, 2010, 53(3): 717-728.

[21] 张玉娥, 牛润明. 引入无限元的地铁区间隧道地震反应分析[J]. 石家庄铁道学院学报, 2001, 14(3): 71-74.

ZHANG Yue, NIU Runming. Studying on the response of subway tunnel subjected to earthquake loading[J]. Journal of Shijiazhuang Railway Institute, 2001, 14(3): 71-74.

[22] 姜忻良, 谭丁, 姜南. 交叉隧道地震反应三维有限元和无限元分析[J]. 天津大学学报, 2004, 37(4): 307-310.

JIANG Yinliang, TAN Ding, JIANG Nan. 3D finite and infinite element analysis for seismic response of intersecting tunnel[J]. Journal of Tianjin University, 2004, 37(4): 307-310.

[23] 朱军, 唐章宏, 顿月芹, 等. 无限元法在三维电测井计算中的应用[J]. 天然气工业, 2008, 28(11): 59-61.

ZHU Jun, TANG Zhanghong, DUN Yueqin, et al. Application of infinite element method(IEM) to 3D electric logging calculation[J]. Natural Gas Industry, 2008, 28(11): 59-61.

[24] 徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994: 159-170.

XU Shizhe. Finite element method for geophysics[M]. Beijing: Science Press, 1994: 159-170.

[25] 刘德贵, 费景高, 于泳江, 等. FORTRAN算法汇编(一)[M]. 北京: 国防工业出版社, 1980: 204-208.

LIU Degui, FEI Jinggao, YU Yongjiang, et al. FORTRAN program for algorithm(1)[M]. Beijing: National Defense industry Press, 1980: 204-208.

[26] TANG Jingtian, WANG Feiyan, XIAO Xiao, et al. 2.5D DC resistivity modeling considering flexibility and accuracy[J]. Journal of Earth Science, 2011, 22(1): 124-130.

[27] TANG Jingtian, WANG Feiyan, REN Zhengyong, et al. 3D direct current resistivity forward modeling by adaptive multigrid finite element method[J]. J Cent South Univ Technol, 2010, 17(3): 587-592.

[28] Cecot W, Rachowicz W, Demkowicz L. An hp-adaptive finite element method for electromagnetics. Part 3: A three-dimensional infinite element for Maxwell’s equations[J]. International Journal for Numerical Methods in Engineering, 2003, 57: 899-921.

[29] REN Zhengyong, TANG Jingtian. 3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method[J]. Geophysics, 2010, 75: 7-17.

[30] R

cker C, G

nther T, Spitzer K. Three-dimensional modelling and inversion of dc resistivity data incorporating topography-I. Modelling[J]. Geophysical Journal International, 2006, 166: 495-505.

[31] XU Shizhe, ZHAO Shengkai, NI Yi. A boundary element method for 2D resistivity modeling with a point current source[J]. Geophysics, 1998, 63(2): 399-404.

(编辑陈灿华)

收稿日期：2014-02-17；修回日期：2014-04-21

基金项目：国家公益性行业基金资助项目(SinoProbe-03)；国家自然科学基金资助项目 (41174105，41104071，41204082)；中南大学研究生学位论文创新基金资助项目(2011ssxt063)

通信作者：原源(1989-)，女，山西运城人，博士研究生，从事三维直流电阻率有限元正反演研究；电话：13657400521；E-mail：yuanyuanhaha@gmail.com

摘要：为了解决传统有限元截断边界所引起的问题，提出一种新的2.5D直流电阻率有限元-无限元耦合数值模拟方法。首先推导无限元2.5D单元映射函数，然后提出一种无限元形函数，将其与传统有限元相结合，取代传统的混合边界，使得电位在无限域内连续并在无限远处衰减为0 V，最终形成的刚度矩阵稀疏对称并与场源位置无关。研究结果表明：在相同的网格剖分下，有限元无限元耦合方法比传统有限元法能够在边界测点处得到更高的计算精度，能够在较小的计算范围内得到更优的计算结果，从而有利于减少节点数，提高计算速度；由于系数矩阵不随场源位置改变，有利于加速反演计算。