螺栓联接梁动力学模型及其参数辨识方法
王伯平1,翟敬宇2,孙伟3,陈玉刚2,韩清凯2
(1. 空军航空大学 航空理论系,吉林 长春,130022;
2. 大连理工大学 机械工程学院,辽宁 大连,116024;
3. 东北大学 机械工程与自动化学院,辽宁 沈阳,110819)
摘 要:
的螺栓联接梁,采用线性弯曲刚度和立方刚度等参数来表征该系统联接部位的非线性特性,结合边界条件和联接部位的连续性条件,建立其二自由度非线性动力学模型。采用多尺度法对该系统进行求解,获得其非线性频率响应函数。在非线性解的基础上,推导出系统的线性和非线性参数的表达式。以某悬臂螺栓联接梁为例,实测不同预紧力矩下的固有特性和响应特性,进而辨识出不同预紧力矩下该系统的线性和非线性参数。结果表明:本文提出的螺栓联接梁二自由度非线性模型以及相应的参数辨识方法具有合理性,螺栓联接梁具有典型的软式非线性特性。
关键词:
螺栓联接梁;非线性动力学模型;频率响应函数;多尺度法;参数辨识;
中图分类号:V414 文献标志码:A 文章编号:1672-7207(2013)11-4483-09
Dynamic model and parameter identification method of bolted joint beam
WANG Boping1, ZHAI Jingyu2, SUN Wei3, CHEN Yugang2, HAN Qingkai2
(1. Department of Flight Theory, Aviation University of Air Force, Changchun 130022, China;
2. School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China;
2. School of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, China)
Abstract: For the cantilever bolted joint beam, parameters including linear bending stiffness and cubic stiffness were introduced to represent the nonlinear characteristics of the joint part. Combined with the boundary conditions and the continuity of joint part, a two degree of freedom (DOF) nonlinear dynamic model was constructed and the nonlinear frequency response function was obtained by means of multiple scales method. Based on the nonlinear solutions, expressions of linear and nonlinear parameters were deduced. A cantilever beam with bolted joint was taken as example to identify the linear and nonlinear parameters by measuring its natural characteristics and response characteristics at different preloads. The results show that the two DOF model and the identification method are reasonable. Typical “softening” nonlinearities can be also observed in the results.
Key words: bolted joint beam; nonlinear dynamic model; frequency response function; multiple scale method; parameter identification
螺栓联接方式是机械结构中常见的联接形式,在交通、航空、航天、能源、建筑以及各种通用机械设备中广泛应用。从机械动力学的角度,由于联接界面的存在会造成结构系统局部刚度和阻尼的非线性,在某些情况下其动力特性比较复杂,甚至出现分频振动、分岔和混沌等现象[1]。螺栓联接梁是这类组合结构的典型代表,同样具有复杂的动力学特性,其联接部位具有非线性特性。
在工程实际分析中,很多情况下将螺栓联接梁进行动力学简化处理。通常是基于线性化思想,将联接视为线性弹簧和线性阻尼的组合,采用模型修正或实验辨识的方法给出相应的等效参数。这种处理方法忽略了螺栓联接的非线性本质,不能描述由于联接界面存在而导致的复杂非线性现象。另外,人们还采用虚拟材料法和接触单元法来建立螺栓联接结构的非线性有限元模型[2-3],这些模型比较复杂且不容易使用。因此,建立一个合理的、非线性特性的、简化的螺栓联接梁动力学模型十分重要[4]。
螺栓联接部位的非线性特性主要源于其结合面摩擦、滑移和产生间隙时的拍击。有关结合面的接触、摩擦非线性特性的研究已经有很多成果[5-7]。Iwan模型用多个弹簧-滑块组合元素来表达材料和结构的迟滞,具有通用性[8]。采用改进的Iwan梁模型可以用于模拟装配体中的螺栓联接结构的非线性现象[9],并且得到了实验证明[10]。联接部位的动力学特性往往具有软式特征,例如,实验观察到组合结构固有频率下降[11]、不同预紧力矩和激振力幅下的滞后回线的变化[12]等。因此,螺栓联接梁的动力学模型中,必须考虑其联接部位所特有的非线性特性。
针对螺栓联接梁建立的动力学模型,确定其模型参数特别是非线性环节的参数十分重要。对于非线性动力学系统的模型参数辨识问题,主要有时域和频域2类方法。模型参数的时域辨识方法容易实施,但易受测量误差的影响[13-14]。频域辨识方法可以避免数据处理中算法复杂问题,但是在试验方法和理论推导上要求较高,且更适用于弱非线性系统[15-16]。
基于非线性系统的多尺度分析方法,可以方便地求解常规非线性动力学方程,获得其非线性频率响应函数,进而实现其非线性参数辨识。这种基于多尺度法的频域参数识别方法类似于直接识别频响函数的骨干曲线,简洁直观。采用这种方法,人们获得了含有几何和材料非线性的悬臂梁的非线性参数[17],也实现了自由态下螺栓联接梁的非线性参数辨识[18]。
针对处于悬臂状态的螺栓联接梁,本文作者建立二自由度的、具有立方项非线性特性的弯曲变形动力学方程。结合悬臂边界条件和结合部连续性条件,采用多尺度法进行求解,分别获得线性尺度下的频率响应函数和非线性一阶近似尺度下的频率响应函数。结合实验测试,求解出螺栓联接梁的线性和非线性参数具体值。最后比较了在不同激振力幅作用下的螺栓联接梁的软式非线性的变化。
1 螺栓联接梁的动力学模型及其解析解
1.1 两段梁模型及其螺栓联接部位非线性环节
图1(a)所示为螺栓联接梁结构,它由2个梁通过单个螺栓联接组成,螺栓联接组合梁一端固定,另一端自由。其二自由度非线性模型如图1(b)所示,其中,K1,Kθ分别表示线性剪切刚度和弯曲刚度,K3表示立方项刚度,C表示结合部的黏性阻尼系数。
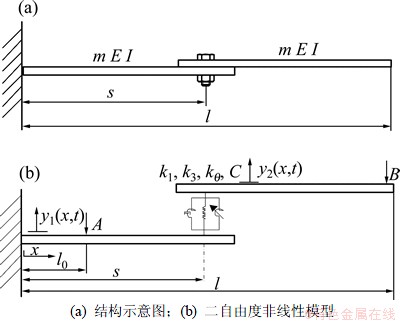
图1 螺栓联接梁结构及简化模型
Fig.1 Bolted joint beam structure and simplified model
根据Euler-Bernoulli梁理论,建立该螺栓联接梁的二自由度弯曲变形的运动微分方程[19]:
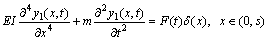 (1)
(1)
 (2)
(2)
式中:m,E和I分别为梁的单位长度质量、弹性模量和惯性矩;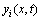 为梁的横向位移。
为梁的横向位移。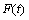 为作用在点
为作用在点
A处的外载荷;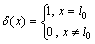 。
。
考虑边界条件和联接处的连续性条件,其悬臂状态的边界条件为:
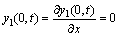 (3)
(3)
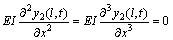 (4)
(4)
在联接部两侧的剪力和弯矩应该相等,即在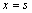 处由弯矩相等可得
处由弯矩相等可得
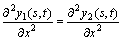 (5)
(5)
由剪力相等可得
 (6)
(6)
设K1为联接部位处的剪切刚度,由剪力平衡可得
 (7)
(7)
螺栓联接部位非线性特性用线性弯曲刚度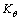 、立方项刚度K3和黏性阻尼系数C组合起来表征,这样,由联接部位的弯矩平衡关系可得
、立方项刚度K3和黏性阻尼系数C组合起来表征,这样,由联接部位的弯矩平衡关系可得
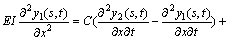
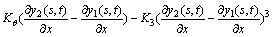 (8)
(8)
1.2 基于多尺度法的螺栓联接梁的解析解
对于螺栓联接梁的线性一阶固有频率附近的主共振状态,可以将外激励视为小参数项,根据多尺度法[20],令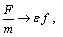
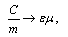
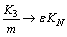 ,运动微分方程(1)和(2)可以转化为
,运动微分方程(1)和(2)可以转化为
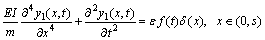 (9)
(9)
 (10)
(10)
外激励的频率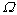 接近结构的一阶固有频率,即
接近结构的一阶固有频率,即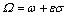 ,式中,
,式中,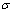 为解谐参数,
为解谐参数,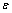 为小参数。
为小参数。
将螺栓联接梁运动微分方程的解用不同的时间尺度来表达,如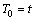 ,
,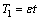 ,对于线性部分有
,对于线性部分有
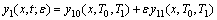 (11)
(11)
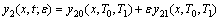 (12)
(12)
将线性解析表达式(11)和(12)带入方程(1)~(8),化简整理,令方程两侧的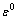 和
和 项系数分别相等,获得在一阶固有频率附近的主共振状态下的运动微分方程、边界条件和连续性条件在不同时间尺度下的方程。
项系数分别相等,获得在一阶固有频率附近的主共振状态下的运动微分方程、边界条件和连续性条件在不同时间尺度下的方程。
(1) 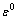 阶项
阶项
运动微分方程
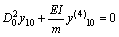 (13)
(13)
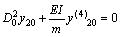 (14)
(14)
边界条件
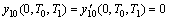 (15)
(15)
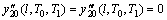 (16)
(16)
连续性条件
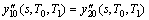 (17)
(17)
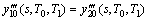 (18)
(18)
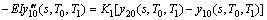 (19)
(19)
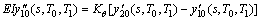 (20)
(20)
(2)  阶项
阶项
运动微分方程
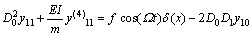 (21)
(21)
 (22)
(22)
边界条件
 (23)
(23)
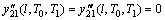 (24)
(24)
连续性条件
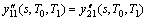 (25)
(25)
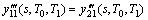 (26)
(26)
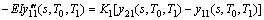 (27)
(27)
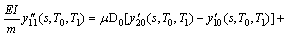
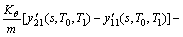
 (28)
(28)
式中: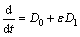 ,
,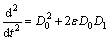 ,
,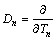 ,
,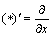 ,
, 。
。
分别对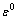 阶和
阶和 阶的方程进行求解。
阶的方程进行求解。
(1) 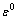 阶项齐次方程的一阶共振响应。设解的形式为
阶项齐次方程的一阶共振响应。设解的形式为
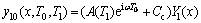 (29)
(29)
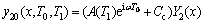 (30)
(30)
式中: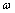 为结构的一阶固有频率,Cc为前项的复共轭,
为结构的一阶固有频率,Cc为前项的复共轭,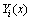 为一阶共振响应的振型函数。
为一阶共振响应的振型函数。
将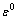 阶项的解式(29)和(30)带入
阶项的解式(29)和(30)带入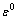 阶项的方程中,式(13)~(20)可转换为
阶项的方程中,式(13)~(20)可转换为
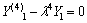 (31)
(31)
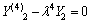 (32)
(32)
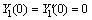 (33)
(33)
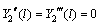 (34)
(34)
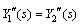 (35)
(35)
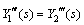 (36)
(36)
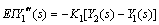 (37)
(37)
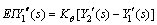 (38)
(38)
式中: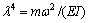 。
。
由式(31)和(32),可将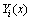 表示为
表示为
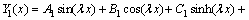
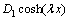 (39)
(39)
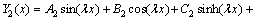
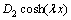 (40)
(40)
进而可根据式(33)和(34)的边界条件和(35)~(38)的连续性条件确定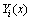 中系数Ai,Bi,Ci,Di。
中系数Ai,Bi,Ci,Di。
(2)  阶项非齐次方程的摄动解。设方程组的解为由长期项
阶项非齐次方程的摄动解。设方程组的解为由长期项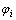 和非长期项Vi组成
和非长期项Vi组成
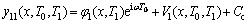 (41)
(41)
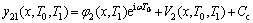 (42)
(42)
将方程的解带入 阶项的方程中,令方程两侧的长期项系数相同,从而消除长期项,则式(21)~(28)可转换为
阶项的方程中,令方程两侧的长期项系数相同,从而消除长期项,则式(21)~(28)可转换为
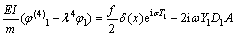 (43)
(43)
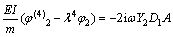 (44)
(44)
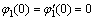 (45)
(45)
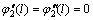 (46)
(46)
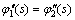 (47)
(47)
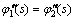 (48)
(48)
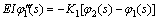 (49)
(49)
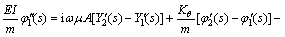
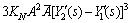 (50)
(50)
考虑到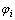 与Yi为伴随解,可以将式(43)和(44)分别乘以Y1和Y2,并沿x方向进行积分,相加可得
与Yi为伴随解,可以将式(43)和(44)分别乘以Y1和Y2,并沿x方向进行积分,相加可得
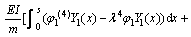

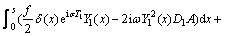
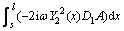 (51)
(51)
经分部积分,再引入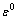 阶项和
阶项和 阶项的边界条件和连续性条件,式(51)可以转换为
阶项的边界条件和连续性条件,式(51)可以转换为
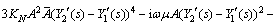
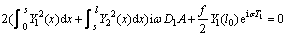 (52)
(52)
根据式(52)求解螺栓联接梁的非线性频率响应函数。令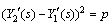 ,
, ,则式(52)可以转换为
,则式(52)可以转换为
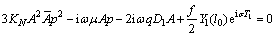 (53)
(53)
该式是关于振幅A的一阶微分方程式,设其解的形式为
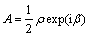 (54)
(54)
将式(54)代入式(53),分成实部和虚部,对于稳态运动的情况,即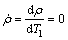 ,
,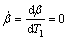 时,可推得如下非线性频率响应函数方程
时,可推得如下非线性频率响应函数方程
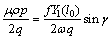 (55)
(55)
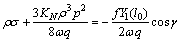 (56)
(56)
相应地,螺栓联接梁的一阶幅频共振曲线方程为
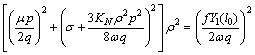 (57)
(57)
式中: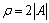 ,
, ,
,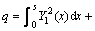
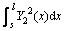 。
。
2 螺栓联接梁模型参数的辨识方法
2.1 线性参数项的识别
根据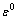 阶项方程的解(式(39)和(40)),带入
阶项方程的解(式(39)和(40)),带入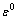 阶项的边界条件和连续性条件(式(33)~(38)),可得
阶项的边界条件和连续性条件(式(33)~(38)),可得
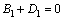 ,
,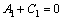 (58)
(58)
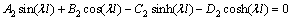
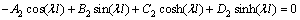 (59)
(59)
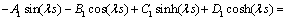
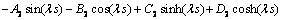 (60)
(60)
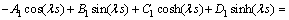
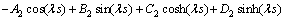 (61)
(61)
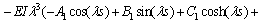
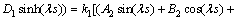
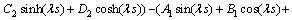
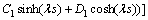 (62)
(62)
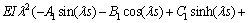
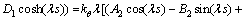
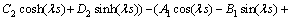
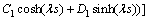 (63)
(63)
以上8个方程是关于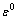 阶项的方程解中Ai,Bi,Ci,Di的方程组。据可解性条件,其系数的行列式必须为0。对于该行列式中,E,I,s,l等参数可以根据试验对象几何参数和材料直接确定。
阶项的方程解中Ai,Bi,Ci,Di的方程组。据可解性条件,其系数的行列式必须为0。对于该行列式中,E,I,s,l等参数可以根据试验对象几何参数和材料直接确定。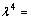
 也可以根据结构测试的线性固有频率计算获得。因此,求解该行列式的秩,对应于不同的线性固有频率可得到关于k1和kθ的二元二次方程组,进而求得相应的线性固有频率和振型函数。
也可以根据结构测试的线性固有频率计算获得。因此,求解该行列式的秩,对应于不同的线性固有频率可得到关于k1和kθ的二元二次方程组,进而求得相应的线性固有频率和振型函数。
2.2 非线性参数项的识别
对于获得的非线性幅频响应共振曲线式(57),进一步做如下变换
 (64)
(64)
根据频响函数的性质[21],在频响函数的峰值处,式(64)满足
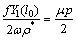 (65)
(65)
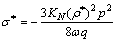 (66)
(66)
式中: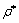 和
和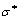 分别为在结构非线性频响函数峰值处的响应幅值和解谐参数。
分别为在结构非线性频响函数峰值处的响应幅值和解谐参数。
在方程的两侧同时乘以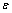 ,并转换成物理参数,得到原非线性系统中具体参数的表达式为
,并转换成物理参数,得到原非线性系统中具体参数的表达式为
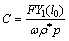 (67)
(67)
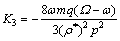 (68)
(68)
式中: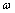 为结构的线性固有频率;
为结构的线性固有频率;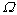 为非线性频响函数的峰值频率。
为非线性频响函数的峰值频率。
3 实例与讨论
3.1 实测过程及其数据分析
对某一螺栓联接梁进行振动测试,实验装置如图2所示。在实验过程中用定力矩扳手将试件安装在夹具上且保持不变。
测试不同激振力幅值、不同螺栓预紧力矩下的联接梁在一阶固有频率附近多个频率点下的振动响应。在一阶固有频率附近的频带设为26.9~28.4 Hz,采用定频定幅激励的方式。激振力幅值分别为2,4,6 N,螺栓预紧力矩分别为3,5,10,15 N·m。
图3所示为不同螺栓预紧力矩、不同激振力幅值下测得的螺栓联接梁的振幅随频率变化的曲线。

图2 螺栓联接梁的实验测试装置
Fig.2 Experiment testing of bolted joint beam
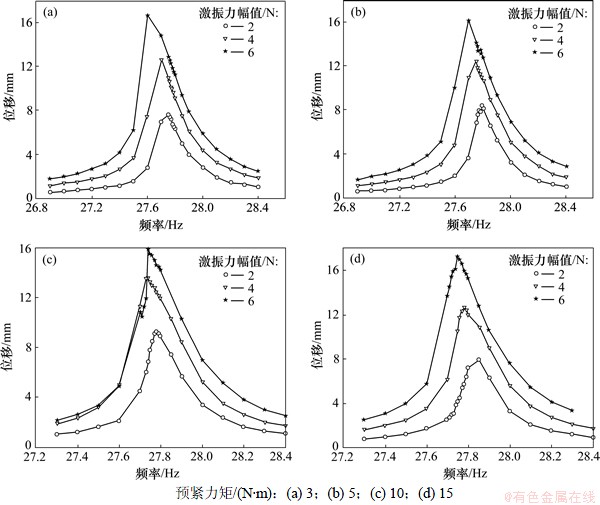
图3 不同预紧力矩下螺栓联接组合梁的幅频响应
Fig.3 Frequency response of bolted joint beam under different levels of bolt preload
从图3可以看出,在相同的螺栓预紧力矩下,随着激振力幅值的增加,共振峰值点所对应的频率会减小,表现出软式非线性。
3.2 线性参数的识别
表1所示为根据上述实测螺栓联接梁幅频响应曲线的共振峰值点所对应的线性固有频率。从表1可以看出,在螺栓预紧力矩变化的情况下,螺栓联接梁的线性固有频率会有一定变化。
根据获得的螺栓联接梁线性固有频率,采用本文方法识别相应的线性参数。
已知螺栓联接梁的材料参数为弹性模量E=2.0×1011 Pa、惯性矩I=5.4×10-10 m4、结构总长l=0.405 m、螺栓位置s=0.185 m、单位长度质量m=1.413 kg/m。
根据式(58)~(63),获得振型函数系数Ai,Bi,Ci,Di (i=1, 2)的方程组,进而令其行列式的秩为0得到关于剪切刚度k1和弯曲刚度kθ的一个二元二次方程。对应着实测得到的4阶线性固有频率,可得到关于k1和kθ的4个方程,具体为
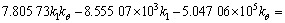
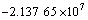
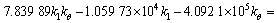
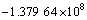
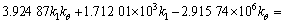
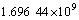
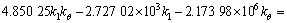
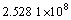 (69)
(69)
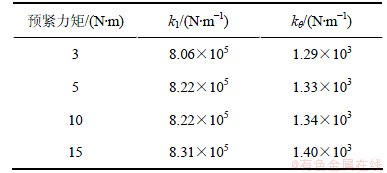
对式(69)进行图解法[23]求解,可以获得在螺栓预紧力矩分别为3,5,10和15 N·m时的螺栓联接梁结合部位的剪切刚度k1和弯曲刚度kθ如表2所示。由于结构的固有频率变化非常小,求解出的剪切刚度k1和弯曲刚度kθ差别也非常小。
表1 不同预紧力矩下螺栓联接梁的线性固有频率
Table 1 Linear natural frequencies of bolted joint beam under different levels of bolt preload
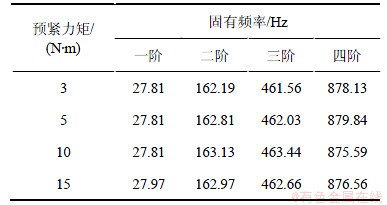
表2 不同预紧力矩下螺栓联接梁的剪切刚度和弯曲刚度
Table 2 Shear stiffness and bending stiffness of bolted joint beam under different levels of bolt preload
3.3 非线性参数的识别
将实验测试所得到的结构响应峰值频率和幅值代入式(67)和(68),可以识别在一定的螺栓预紧力矩和激励力幅时的螺栓联接梁的阻尼C和非线性参数K3。
表3所示为螺栓联接梁上的螺栓预紧力矩分别为3,5,10和15 N·m时,联接梁响应的峰值频率和幅值,以及识别得到的阻尼系数和立方刚度项系数。
3.4 识别结果对比
根据识别出的线性和非线性模型参数,可以获得关于螺栓联接梁的完整动力学模型。根据式(64),预测结构在一阶固有频率处的非线性频率响应曲线。如图4所示为螺栓预紧力矩为15 N·m时实验测试和解析预测所得到的一阶共振曲线对比。
从图4可以看出,在共振峰值处,解析预测的结果与实验测试结果相吻合。在非共振峰值处,实验测试的幅值要高些。因此,根据上述共振曲线的符合情况,可以认为本文提出的螺栓联接梁的软式立方非线性刚度模型及其相应的参数识别方法,具有合理性。
表3 不同预紧力矩下螺栓联接梁的非线性参数
Table 3 Nonlinear parameters of bolted joint beam under different levels of bolt preload
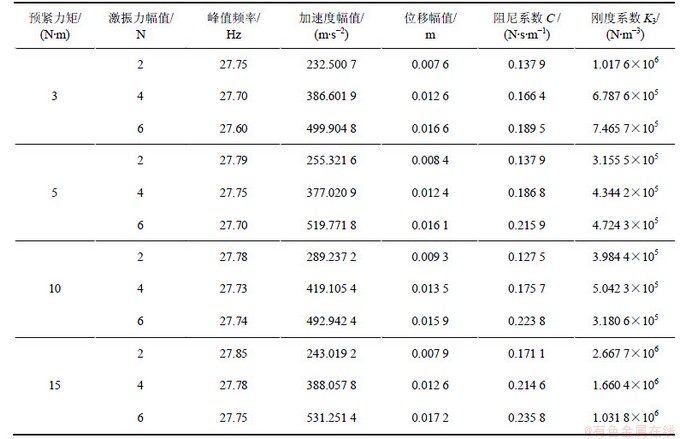
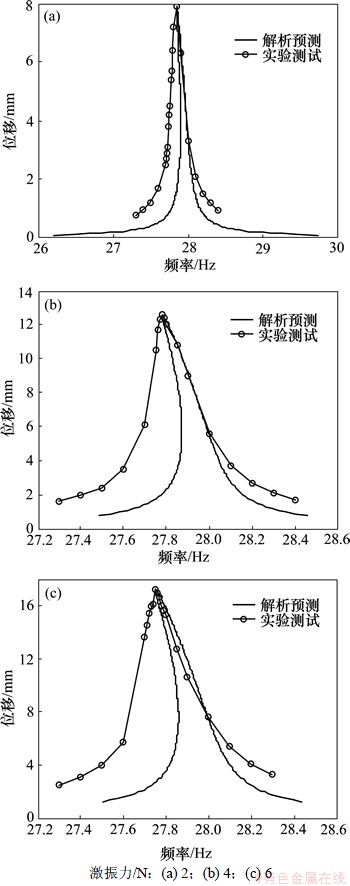
图4 不同激振力下螺栓联接梁的幅频响应曲线
Fig.4 Frequency responses of bolted joint beam under different levels of excitations
4 结论
(1) 建立了螺栓联接梁的二自由度非线性动力学模型,引入了表征螺栓联接部位的立方非线性刚度项和黏性阻尼项,该模型具有合理性,能够反映螺栓联接梁的动力学特性。
(2) 采用多尺度法,利用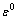 阶和
阶和 阶的螺栓联接梁的非线性频率响应解析解,在此基础上可实现线性模型参数和非线性参数模型参数的合理辨识。首先通过实验测试获得螺栓联接梁的线性固有频率,然后基于系统
阶的螺栓联接梁的非线性频率响应解析解,在此基础上可实现线性模型参数和非线性参数模型参数的合理辨识。首先通过实验测试获得螺栓联接梁的线性固有频率,然后基于系统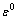 阶频响结果来辨识螺栓联接部位的线性剪切刚度和弯曲刚度。最后,基于系统的
阶频响结果来辨识螺栓联接部位的线性剪切刚度和弯曲刚度。最后,基于系统的 阶频响结果,与不同力幅下的频率响应函数进行对比,辨识得到非线性刚度系数。
阶频响结果,与不同力幅下的频率响应函数进行对比,辨识得到非线性刚度系数。
(3) 随着螺栓预紧力矩的增大,螺栓联接部位的线性刚度不断增大,而非线性刚度先减小后增大;该模型可以较好地表征其软式非线性特性,且在共振区域内的预测结果要比非共振区内的更准确。
参考文献:
[1] Hartwigsen C J. Dynamics of jointed beam structures: Computational and experimental studies[D]. Urbana: University of Illinois at Urbana-Champaign. Aeronautical and Astronautical Engineering Department, 2002: 1-4.
[2] Abad J, Franco J, Celorrio R, et al. Design of experiments and energy dissipation analysis for a contact mechanics 3d model of frictional bolted lap joints[J]. Advances in Engineering Software, 2011, 45(1): 42-53.
[3] Kim J, Yoon J C, Kang B S. Finite element analysis and modeling of structure with bolted joints[J]. Applied Mathematical Modelling, 2007, 31(5): 895-911.
[4] Segalman D J, Gregory D L, Starr M J, et al. Handbook on dynamics of jointed structures[R]. Alberquerque: Sandia National Laboratories, 2009: 10-20.
[5] Ferri A. Friction damping and isolation systems[J]. Journal of Vibration and Acoustics, 1995, 117(B):196-206.
[6] Gaul L, Nitsche R. The role of friction in mechanical joints[J]. Applied Mechanics Reviews, 2001, 54(2): 93-106.
[7] Berger E. Friction modeling for dynamic system simulation[J]. Applied Mechanics Reviews, 2002, 55(6): 535-577.
[8] Iwan W D. A distributed-element model for hysteresis and its steady-state dynamic response[J]. Journal of Applied Mechanics, 1966, 4(33): 893-900.
[9] Song Y, Hartwigsen C, Mcfarland D, et al. Simulation of dynamics of beam structures with bolted joints using adjusted iwan beam elements[J]. Journal of Sound and Vibration, 2004, 273(1): 249-276.
[10] Gaul L, Lenz J. Nonlinear dynamics of structures assembled by bolted joints[J]. Acta Mechanica, 1997, 125(1): 169-181.
[11] Hartwigsen C J, Song Y, Mcfarland D M, et al. Experimental study of non-linear effects in a typical shear lap joint configuration[J]. Journal of Sound and Vibration, 2004, 277(1): 327-351.
[12] Ouyang H, Oldfield M, Mottershead J. Experimental and theoretical studies of a bolted joint excited by a torsional dynamic load[J]. International Journal of Mechanical Sciences, 2006, 48(12): 1447-1455.
[13] Mohammad K, Worden K, Tomlinson G. Direct parameter estimation for linear and non-linear structures[J]. Journal of Sound and Vibration, 1992, 152(3): 471-499.
[14] Yasuda K, Kamiya K. Experimental identification technique of nonlinear beams in time domain[J], Nonlinear Dynamics, 1999, 18(2): 185-202.
[15] Krauss R W, Nayfeh A H. Experimental nonlinear identification of a single mode of a transversely excited beam[J]. Nonlinear Dynamics, 1999, 18(1): 69-87.
[16] Yasuda K, Kamiya K, Komakine M. Experimental identification technique of vibrating structures with geometrical nonlinearity[J]. Journal of Applied Mechanics, 1997, 64(2): 275-290.
[17] Malatkar P. Nonlinear vibrations of cantilever beams and plates[D]. Blacksburg: Virginia Polytechnic Institute and State University. Department of Engineering Science and Mechanics, 2003: 1-115.
[18] Ahmadian H, Jalali H. Identification of bolted lap joints parameters in assembled structures[J]. Mechanical Systems and Signal Processing, 2007, 21(2): 1041-1050.
[19] Rao S S. Mechanical vibrations[M]. 5th ed. Englewood Cliffs: Prentice Hall, 2010: 1-94.
[20] Nayfeh A H, Mook D T. Nonlinear oscillations[M]. Weinheim: Wiley-VCH, 1995: 394-408.
[21] Ahmadian H, Mottershead J, Friswell M. Boundary condition identification by solving characteristic equations[J]. Journal of Sound and Vibration, 2001, 247(5): 755-763.
(编辑 赵俊)
收稿日期:2012-09-10;修回日期:2013-01-12
基金项目:国家重点研究发展计划项目(2012CB026000);国家自然科学基金资助项目(51175070)
通信作者:韩清凯(1969-),男,山东济宁人,教授,博士生导师,从事机械动力学研究;电话:0411-84706750;E-mail: hanqingkai@dlut.edu.cn
摘要:针对处于悬臂态的螺栓联接梁,采用线性弯曲刚度和立方刚度等参数来表征该系统联接部位的非线性特性,结合边界条件和联接部位的连续性条件,建立其二自由度非线性动力学模型。采用多尺度法对该系统进行求解,获得其非线性频率响应函数。在非线性解的基础上,推导出系统的线性和非线性参数的表达式。以某悬臂螺栓联接梁为例,实测不同预紧力矩下的固有特性和响应特性,进而辨识出不同预紧力矩下该系统的线性和非线性参数。结果表明:本文提出的螺栓联接梁二自由度非线性模型以及相应的参数辨识方法具有合理性,螺栓联接梁具有典型的软式非线性特性。


