
J. Cent. South Univ. (2019) 26: 1897-1909
DOI: https://doi.org/10.1007/s11771-019-4143-2
Optimal fuzzy switch placement to increase automation level of electric distribution network considering asset management principles
POUYA Salyani, JAVAD Salehi
Department of Electrical Engineering, Azarbaijan Shahid Madani University, Tabriz, Iran
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract:
Since distribution sector is inherent into high amount of failures, distribution companies (DISCOs) are responsible of attaining an acceptable value for the reliability indices and otherwise they will face up to complaints. So they are usually obligated by regulators to invest on reliability improvement of network. But this investment on reliability is usually from the DISCO’s viewpoint and is also irrespective of customer satisfaction level. In other words, customers are not at the same level of sensitivity to interruptions but DISCO improves the reliability of network without considering the differences in importance degree of loads and their level of reliability requirement. On the other hand DISCOs attempt to reduce their investment costs as much as possible. This paper introduces a novel approach in the field of joint switch placement that can reduce the switch cost from the perspective of asset management policies. To this end, two switch placement plannings in different types of strategies are performed to compare their results. Firstly as witch placement is performed based on reducing the total energy not supplied (ENS) of the system. Then by revising the strategy, a fuzzy switch placement is performed from the DISCO’s point of view which just considers the total ENS of load points most sensitive to interruptions known as important or critical loads. Furthermore, by meeting the related constraints, the reliability of low sensitive customers is disregarded. This is a load importance based planning which can result in switch cost reduction relative to the amount achieved in previous strategy and implies the management of risks associated with reliability and respective constraint. Fuzzy method and new switching mechanism in fuzzy environment of network are implemented to modeling and controlling the risks associated to ENS of critical loads and also the ENS of system.
Key words:
Cite this article as:
POUYA Salyani, JAVAD Salehi. Optimal fuzzy switch placement to increase automation level of electric distribution network considering asset management principles [J]. Journal of Central South University, 2019, 26(7): 1897-1909.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-019-4143-21 Introduction
The public utilities in monopolized structure seek to improve the power system indices within a minimum investment cost. By restructuring of electric power industry, privatization of these utilities seems to be necessary.
One of the objectives of these companies is to set the system indices to just an acceptable level but not necessarily the best level which imposes less investment cost compared to the one in monopolized structure. But a problem here is the risks exposed to the power system. This problem is highlighted in distribution sector where it is usually confronted with weakness of its components and lack of protection devices and consequently lack of reliability. It is preferable for distribution companies (DISCOs) to undertake such risks but in turn it leads to considerable reliability attenuation and unsatisfactory growth by customers.
Applying asset management policies by DISCO is the best solution to reach a trade-off between investment cost and risk of reliability. Asset management as a strategy helps to maximize the profit by minimizing the exposed risks in the system. In distribution sector, asset management is categorized into three periods, short term, mid-term and long term. Reliable operation of system is considered the short term asset management [1]. In Ref. [2], in addition of discussion about asset management and its relation with risk management, quantitative risk analysis (QRA) method is implemented to study the difficulties associated with it.
In Ref. [3], from the asset management perspective, the critical components are identified, which are prioritized to maintenance scheduling. Also the effect of preventive maintenance based on asset management was shown in Ref. [4] by developing a relevant failure rate model. Risk analysis and decision support under uncertainty were used in Ref. [5] to evaluate the maintenance and reinvestment strategy in distribution system asset management.
One of the important and low cost methods utilized in distribution network to increase the reliability level is placement of sectionalizing switches. BILLINTON et al [6] have solved the optimal switch placement problem within a test system with different customer damage functions. In Ref. [7], the distribution network was automated by equipping the system to the automated switches and set of manual switches are defined in Ref. [8] to be upgraded to automatic switches in a smart distribution system.
In Ref. [9], manual switches are used as tie switches combined with automatic switches that is cost effective and results in reduction of system energy not supplied (ENS). Some control sequences also were introduced in Ref. [10] to have a best operation of joint automatic and manual sectionalizing switches in a coordinated manner. Then using weighting coefficients in the objective function, the outage duration for critical load points has a reduction more than noncritical loads.
In the context of solving optimal switch placement problem as a multi-objective optimization, it was proposed to minimize both number of switches and number of customers not supplied in Ref. [11]. In Ref. [12], using multi- objective fuzzy approach, the first objective was the customer interruption cost and the second one is the switch purchasing and maintenance cost.
Switch allocation problem in the presence of distributed generators was discussed in Ref. [13]. Fuzzy multi-objective approach was employed to solve the problem in which the switch cost and reliability are as the two objectives of the planning. In Ref. [14], a new dynamic planning microgrids in a stochastic multi-objective framework was conducted. Along with optimal siting and sizing of distributed energy resources, optimal allocation of switches was also performed for optimal partitioning of distribution network into inter- connected microgrids. In addition to the total investment cost as one of the objectives, the system ENS is applied as the other objective.
In Ref. [15], sectionalizing switch placement problem is presented in a multi-objective approach to improve the system reliability and to optimally determine the number and type of utilized switches. Using NSGA-II as the optimization algorithm, one of the objectives is the switch cost and the two other objectives relate to the reliability indices system average interruption frequency index (SAIFI), and system average interruption duration index (SAIDI). NSGA-II was employed in Ref. [16] to solve the multi-objective switch placement problem and to minimize the three objectives, utility cost, SAIDI and expected customer interruption cost (ECOST). In Ref. [17], by obtaining the Pareto solutions, optimum number and location of sectionalizing switches were determined in which the multi-objective problem consists of the planning cost objective function, the reliability objectives, ASAIDI, ASAIFI and ENS indices.
DISCOs are interested in lowering the investment costs in the network as much as possible. But due to reliability issue and the fact that network requires a minimum level of reliability, and then independent system operator (ISO) forces them to improve the specified indices. Reliability indices such as SAIDI or SAIFI can be the target and each has its own special characteristic; however, ENS index is also applicable in planning problems as commented in Refs. [14, 18, 19]. It reflects the amount of lost energy that is important from the economical aspect. When DISCO reduces the ENS, in addition to increase in amount of sold energy, customers incur less amount of energy shortage too. Here it should be noted that just the system index is important from the DISCO’s viewpoint and it does not matter the reliability level requirement of each load point.
As a matter of fact, considering a residential load and an industrial load like petrochemical, these load points differ from each other in the sensitivity to electricity cut offs and the satisfactory level. For instance, average interruption duration of 8 h per year contributes a substantial monetary loss to the petrochemical unit whereas it sounds trivial to the residential load. Therefore, it is possible for DISCO to be irresponsible to enhance the reliability of customers that can put up with their existing service condition. Instead there exists some important or critical loads that deserve a higher value of reliability. These critical customers can be important due to their high value of lost load (VOLL), strategic circumstances such as military organizations or important public agencies such as municipalities.
In this paper, a novel approach is introduced in planning of distribution system and in the field of switch placement which can have a substantial effect on the investment costs of the companies. According to this approach, DISCO can just concentrate on reducing the total ENS of critical loads instead of total ENS of network considering the technical constraints. On the other hand, the loads with low degree of sensitivity are known as noncritical loads and their ENS can be ignored by DISCO.
By applying this new approach, the switch investment cost can be reduced with respect to the cost amount obtained in conventional planning which is most desirable and beneficial for DISCO. But to serve this goal, there are some constraints about reliability that are inherent to risk to uncertainties existing in the distribution system. These uncertainties are modeled by employing fuzzy numbers and the risk of violation for constraints is controlled by fuzzy mathematic concept. This fuzzy switch placement is in the asset management perspective and has its own switching mechanism that will be completely discussed in following sections.
The objective functions and their associated constraints are modeled in Section 2 along with explanation of the switching mechanism and optimization algorithms. Then the results are assessed in Section 3 and finally the conclusion is given in last section.
2 Method
Before any discussion about the objective functions, it must be mentioned that the switch placement problem in this paper is solved in the presence of uncertainties. These uncertainties can exist in load of buses, failure rate of feeders and switching time of manual switches.
Fuzzy triangular membership function due to its easiness to handle is used to model these uncertainties especially in distribution networks [20–23]. Triangular fuzzy number (TFN) is
represented with three points in the form of 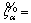
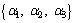 where α1<α2<α3 and its membership function over the real number domain R is as follows:
where α1<α2<α3 and its membership function over the real number domain R is as follows:
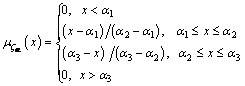 (1)
(1)
This membership function is illustrated in Figure 1. By fuzzy modeling of uncertainties, the load active power in each bus is written as 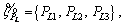 the reactive power as
the reactive power as 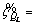
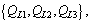 the failure rate per kilometer for feeders as
the failure rate per kilometer for feeders as 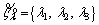 [24] and the switching time for manual switches is shown by
[24] and the switching time for manual switches is shown by 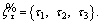
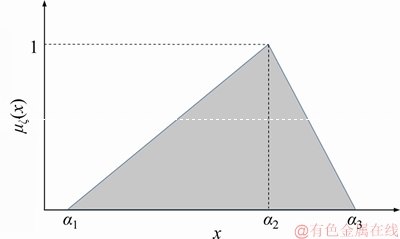
Figure 1 Triangular fuzzy membership function
The paper aims to have a comparative study on optimal switch placement and to show the cost effectiveness of the proposed method. Firstly, as a conventional switch placement, DISCO is responsible of reducing the total system ENS in a minimum investment cost. It must be noticed that because the probabilistic nature of failures occurs in the system, the cost of ENS belongs to the risk strategy of distribution system operator (DSO).
As the customer satisfaction outweighs the profit, the investment on reduction of ENS is increased by DISCO. Another important point that must be emphasized is this investment is from the DISCO viewpoint to reduce the total unsupplied energy of network and the importance degree of customers is not considered. The objective function for the total investment cost in this scenario is represented in Eq. (2) which is modeled by TFN.
The objective function contains two terms. The first one is switch cost and another is the cost of ENS. The switch cost is sum of capital investment cost and maintenance and operation (M&O) cost for both type of switches. Subscripts as and ms denote to the automatic and manual switches.
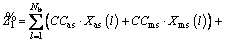
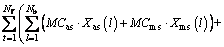
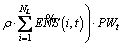 (2)
(2)
where
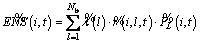 ; (3)
; (3)
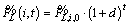 ; (4)
; (4)
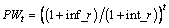 ; (5)
; (5)
X(l) is a binary decision variable that defines if the section l is equipped with switch or not. However, just at the begin, the sections are candidate to switch location. CC and MC indicate the capital investment and maintenance cost for any type of switch respectively. The second term is about total system ENS and its cost in the planning horizon. Parameter ρ is the energy loss price that reflects the value of lost load. As it is seen in Ref. (3), load point ENS is affected by three factors, failure rate  outage duration
outage duration 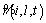 and bus load
and bus load  Outage duration itself is influenced by feeder repair time, switching time and load amount in which all of them can have fuzzy behavior. Also, it is time dependent due to the annual load growth of the network Eq. (4) and its effect on load restoration process of which mechanism will be discussed later. Based on Ref. [23] and TFN arithmetic operations, ENS is a TFN too. The time dependent worth factor is shown by PWt in Eq. (5) where inf _r and int _r are inflation and interest rate, respectively.
Outage duration itself is influenced by feeder repair time, switching time and load amount in which all of them can have fuzzy behavior. Also, it is time dependent due to the annual load growth of the network Eq. (4) and its effect on load restoration process of which mechanism will be discussed later. Based on Ref. [23] and TFN arithmetic operations, ENS is a TFN too. The time dependent worth factor is shown by PWt in Eq. (5) where inf _r and int _r are inflation and interest rate, respectively.
Now in the second scenario, the strategy is revised and a new planning is taken by disregarding the reliability of load points that are noncritical and DISCO is irresponsible of reducing their ENS. In turn, the total ENS reduction of critical loads sensitive to interruptions must be considered. Its reason is that the frequency and duration of electricity interruptions are not often sensitive to the noncritical loads whereas it can cause financial losses to the critical loads.
But it needs to be taken into account up to an acceptable extent that the noncritical loads can incur these interruptions. Furthermore, this strategy just considers the total ENS reduction of important loads from the viewpoint of DISCO and not from the customer viewpoint. In other words, DISCO does not seek to reduce the ENS of each customer specified as critical load and there is no problem if their ENS has not any substantial reduction relative to the value obtained in previous strategy.
Thus it seems to be economical to disregard the investment on reliability of these customers and instead, DISCO can just take into account the total ENS of critical loads. But there are following constraints that must be considered.
By reduction in number of switches, ENS of critical loads must not have any increase relative to the value obtained in conventional switch placement mentioned in previous scenario.
Total system ENS must not exceed the predefined permissible value by applying this strategy in switch placement.
In fact, the main purpose of DISCO is to reduce the switch cost by disregarding the ENS of unimportant loads. Since by reduction in switch cost (change in number or type of switch), it is probable to have increase in ENS of any critical load. The first constraint expresses that by strategy revision and lowering the switch cost, ENS of critical loads must not exceed the value obtained in conventional planning, even though their ENS value does not have a substantial reduction. Also, the second constraint indicates that the network has a maximum level of system ENS and a certain amount of investment on switch placement is necessary.
But these constraints are exposed to risks due to the aforementioned uncertainties. Hence to handle these risks, it is better to solve the load importance based switch placement problem in a multi-objective framework. To this end, two objective functions are discussed below.
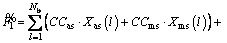
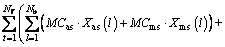
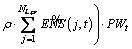 (6)
(6)
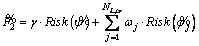 (7)
(7)
where
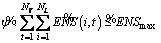 ; (8)
; (8)
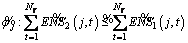 ; (9)
; (9)
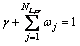 ; (10)
; (10)
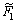 refers to the fuzzy cost function for this scenario which is similar to the objective function
refers to the fuzzy cost function for this scenario which is similar to the objective function 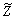 discussed previously; j denotes buses considered critical load points.
discussed previously; j denotes buses considered critical load points.
As it is apparent, the main difference is that just the total ENS of critical loads is taken in the cost function. Therefore, the optimal number and type of switches should be selected in a way to lower the ENS of most sensitive loads. It must be noted that energy loss price is the same as for noncritical loads and has not any increase.
The second objective function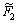 is introduced to handle the risk of satisfying constraints. These risks stem from fuzzy nature of ENS. Fuzzy inequality
is introduced to handle the risk of satisfying constraints. These risks stem from fuzzy nature of ENS. Fuzzy inequality 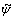 in constraint Eq. (8) is about the total system ENS constraint and
in constraint Eq. (8) is about the total system ENS constraint and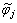 in constraint (9) checks the ENS for each critical load point j. Parameters γ and ωj are the weigh factors and their summation must be equal to 1 shown in Eq. (10). The function Risk(·), measures the risk of violation of fuzzy constraints.
in constraint (9) checks the ENS for each critical load point j. Parameters γ and ωj are the weigh factors and their summation must be equal to 1 shown in Eq. (10). The function Risk(·), measures the risk of violation of fuzzy constraints.
Function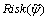 measures the risk of exceeding the maximum permissible value for total system ENS. And
measures the risk of exceeding the maximum permissible value for total system ENS. And 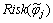 measures the risk of increasing the ENS of each critical load and exceeding the amount obtained in conventional switch placement. In order to calculate these risks, it is better to have a brief review on fuzzy inequalities.
measures the risk of increasing the ENS of each critical load and exceeding the amount obtained in conventional switch placement. In order to calculate these risks, it is better to have a brief review on fuzzy inequalities.
Fuzzy inequalities do not have a certain logic values 0 and 1. But they are ranked in a degree of feasibility between 0 and 1. There are two types of fuzzy inequalities. In first one, the left hand side is a fuzzy number and the right hand side is a script number like 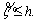
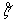 is a TFN and h is a script number. To measure the possibility degree of this inequality, the below function is used considering Figure 2.
is a TFN and h is a script number. To measure the possibility degree of this inequality, the below function is used considering Figure 2.
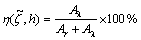 (11)
(11)
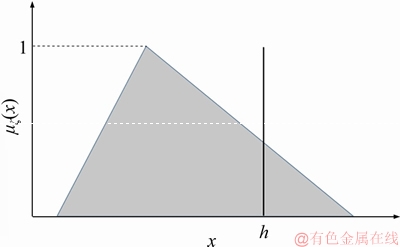
Figure 2 Inequality between a TFN and a script number
In the second type, the comparison is between two fuzzy numbers in the form of  There are several methods to rank the fuzzy numbers discussed in Refs. [25–27]. Fuzzy preference relation is a suitable method to rank two fuzzy numbers [28] and to calculate the degree of coincidence as defined in Eq. (12).
There are several methods to rank the fuzzy numbers discussed in Refs. [25–27]. Fuzzy preference relation is a suitable method to rank two fuzzy numbers [28] and to calculate the degree of coincidence as defined in Eq. (12).
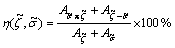 (12)
(12)
where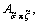
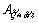
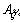 and
and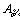 are the areas. This is shown in Figure 3 where
are the areas. This is shown in Figure 3 where  .
.
Moreover, Hamming distance concept [29] is a best way to calculate the preference relation and it is formulated as below. Operator D stands for dominance and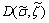 measures the dominance degree of
measures the dominance degree of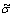 on
on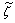 .
.
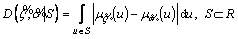 (13)
(13)
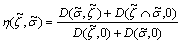 (14)
(14)
The possibility degree of a fuzzy inequality 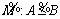 is measured by η(A, B). Now the risk function depending on the kind of inequality for this fuzzy constraint can be described as
is measured by η(A, B). Now the risk function depending on the kind of inequality for this fuzzy constraint can be described as 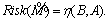 Constraint
Constraint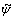 relates to the comparison between a TFN and a crisp number whereas constraints
relates to the comparison between a TFN and a crisp number whereas constraints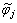 for critical load points belong to the ranking of two TFNs.
for critical load points belong to the ranking of two TFNs.
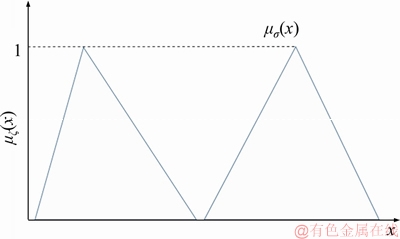
Figure 3 Inequality between two TFN
The two cost functions 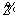 and
and 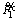 discussed above are in fuzzy domain and they need to be defuzzified. The defuzzification method applied in this paper is using removal function
discussed above are in fuzzy domain and they need to be defuzzified. The defuzzification method applied in this paper is using removal function 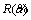 shown in Eq. (15) where
shown in Eq. (15) where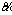 is a TFN in the form of
is a TFN in the form of 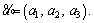
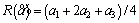 (15)
(15)
2.1 Switching mechanism
By fault occurrence in the network and to have a maximum load restoration, it is important to define a correct outage management or here known as switching mechanism. As the joint switch placement is employed in this paper, fault isolation and load restoration directly depend on location and type of utilized switches in the network. Apart from the load restoration process for the load points upstream the faulted section, load transfer to the adjacent substation is a solution in the restore customers downstream the faulty section. A distribution can have the load transfer capability if there exists a cross connection or reserve feeder.
It can be performed by opening the best switch below the faulty section and transferring the interrupted healthy loads to an adjacent substation. To determine which switch should be opened, the following fuzzy constraints should be considered.
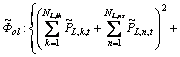
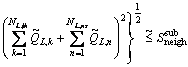 (16)
(16)
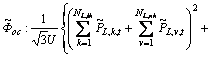
 (17)
(17)
where NL,ih, NL,ns and NL,nf are respectively number of interrupted healthy loads, total number of load points assigned to the neighbor substation and total number of load points in neighbor feeder; 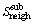 is the rated capacity of neighbor substation that interrupted healthy load must be transferred to it. Parameter
is the rated capacity of neighbor substation that interrupted healthy load must be transferred to it. Parameter 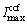 stands for the maximum capacity of cross connection feeder that this load must be transferred through it. Unlike the active power demand that is affected by load growth, the increase of reactive power over the planning period is disregarded. This is due to the capacitors usually installed in the network and their compensation capability. Fuzzy constraints (16) and (17) are about overloading of neighbor substation and overcurrent in the feeder by load transfer operation. The overall risk of violation for these constraints is calculated by Eq. (18).
stands for the maximum capacity of cross connection feeder that this load must be transferred through it. Unlike the active power demand that is affected by load growth, the increase of reactive power over the planning period is disregarded. This is due to the capacitors usually installed in the network and their compensation capability. Fuzzy constraints (16) and (17) are about overloading of neighbor substation and overcurrent in the feeder by load transfer operation. The overall risk of violation for these constraints is calculated by Eq. (18).
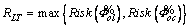 (18)
(18)
where RLT is the risk of improper load transfer named as LT risk. Now to have an appropriate algorithm for load restoration process, a flowchart is represented in Figure 4. As it is shown in this flowchart, a risk level α is introduced to define if the intended switch is below the faulty section operate or not.
This parameter is important in final solution effects on the ENS of load points. It must be noted if it was possible to shed the loads, there was no need to define the best switch to operate. However, it should have its particular mechanism to shed the fuzzy loads and in this paper there is no infrastructure assumed to apply load shedding process.
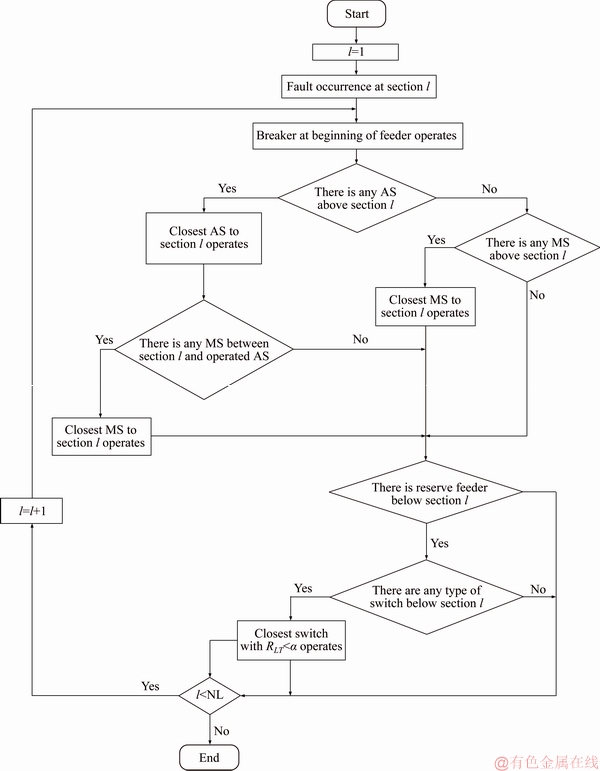
Figure 4 Switching mechanism flowchart (MS: manual switch, AS: automatic switch)
2.2 Optimization algorithms
The two comparative scenarios described before have different types of objective functions. The first scenario concerned with conventional switch placement has a single objective function and the second one is modeled in multi-objective framework. Both of them are in the context of fuzzy optimization that are addressed in Refs. [30, 31]. On the other hand, genetic algorithm (GA) is the proposed algorithm of optimization in this paper. Hence, the conventional switch placement problem is optimized via single objective GA and the load importance based switch placement problem is solved through the non-dominated sorting genetic algorithm (NSGA-II). These two heuristic algorithms and codification of problems are discussed.
2.2.1 Genetic algorithm
Genetic algorithm (GA) is implemented to solve the problem of switch placement in conventional form. GA is based on evolutionary search and reproduction of population. Population is set of solutions that are produced in a random manner. Each solution produced in GA is named a chromosome which is constructed of genomes and is codified like Eq. (19) for this problem.
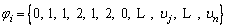 (19)
(19)
The length of these chromosomes is equal to n which is the number of candidate sections in the network. For a sample genome υj=0, the jth section is without any installable switch. If υj=1, the section is equipped with automatic switch and number 2 denotes the manual sectionalizing switch. Three steps are defined for GA optimization. As the first step, population initialization is done by GA to generate random chromosomes. These chromosomes are ranked via fitness function and then must be sorted. It must be reminded that the fitness output is the deffuzificated form of the cost function.
Then by random selection methods, crossover and mutation as reproduction mechanisms are applied to this population over a specific iteration. To apply the crossover operator, roulette wheel is implemented to randomly selecting of two chromosomes φ1 and φ2. Then new individuals are produced by crossover like Eqs. (20) and (21).
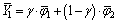 (20)
(20)
 (21)
(21)
To apply the mutation operator on a chromosome, a specific set of genomes are selected based on parameter μ. This chromosome can be mutated by altering each genome υj to another number defined in the set {0, 1, 2}. After finishing the iteration process, the chromosome with the best fitness is selected as the optimum solution.
2.2.2 NSGA II and fuzzy decision making
Non-dominated sorting genetic algorithm (NSGA-II) as a multi-objective evolutionary algorithm (MOEA) is employed in this paper to solve the load importance based planning. NSGA-II apart from the single objective GA consists of three main steps, initial population, crossover and mutation discussed before. Also, this problem is codified as well as conventional switch placement problem solved by GA.
However, selection methods and sorting the solutions are different and have their own mechanism. This algorithm sorts and locates the produced solutions in several frontiers based on the domination concept which were fully discussed in Ref. [32]. The solutions that are non-dominated mean that they dominate other solutions and are not dominated by another one that are all located within a frontier named Pareto frontier. In fact, NSGA-II gives us a set of non-dominated solutions instead of a single optimum point that all of them can be the intended solution for DISCO.
After obtaining the Pareto solutions, it is necessary to select one point among other non- dominated solutions that are economical and acceptable for the planner. Several methods have been introduced to reach the final solution and fuzzy decision making as a well-known method is employed in this paper [33, 34]. Based on fuzzy set theory, a linear membership function is considered for each objective function. The objective function is normalized with Eq. (22) if it is monotonically decreasing; otherwise, Eq. (23) is used.
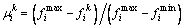 (22)
(22)
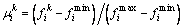 (23)
(23)
where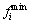 and
and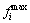 are the minimum and maximum values of the objective I in the set of solutions. This normalization assigns a fuzzy value for each of the Pareto solution k in every objective i. Then for each non-dominated solution, a normalized membership value is defined through Eq. (24) and the solution with a maximum membership value is selected as the best point for the decision maker. Np is the number of Pareto solutions.
are the minimum and maximum values of the objective I in the set of solutions. This normalization assigns a fuzzy value for each of the Pareto solution k in every objective i. Then for each non-dominated solution, a normalized membership value is defined through Eq. (24) and the solution with a maximum membership value is selected as the best point for the decision maker. Np is the number of Pareto solutions.
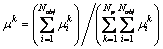 (24)
(24)
3 Results
The 95-bus Thailand real system [35] is introduced in this paper to show the validity and effectiveness of the proposed method shown in Figure 5. It contains six HV/MV substations and eighteen MV feeders. Also, the gray dots are indicator of breaker in the beginning of feeder and the total number of load points is equal to 94. First of all, it must be mentioned that the network is without any sectionalizing switch. The blue dots indicate the tie switches but in this paper, their operation in the faulty mode of system is considered. These tie switches are in manual type and are closed by operator to connect the two feeders.
If the load in bus i is named Pi, then the base load (average load in the first year) as TFN is assumed to be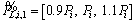 . Failure rate and switching time for manual switch in fuzzy domain are
. Failure rate and switching time for manual switch in fuzzy domain are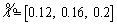 fr/km and
fr/km and 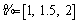 h. Switching time of 10 min is considered for automatic type. Free capacity of all the substations is assumed to be 30% of their base load.
h. Switching time of 10 min is considered for automatic type. Free capacity of all the substations is assumed to be 30% of their base load.
Capital cost and maintenance cost for manual and automatic switch respectively are 4700 $,1500 $, 94 $/a and 50 $/a. Parameters ρ, d, inf_r and int_r are 2 $/(kW·h), 3%, 8% and 12%, respectively. The optimal switch placement problem is studied in two scenarios to have a comparison which is beneficial for DISCO. Numerical results of optimal switch placement for these scenarios are represented at the end of the text.
3.1 Scenario 1: Conventional switch placement
In this scenario, the main goal is to reduce the total ENS of system in the planning horizon using fuzzy approach. All the loads have the same priority from the DISCO viewpoint. In addition, two LT risks of 5% and 30% are considered to observe its effect on the solution. Fuzzy result of total cost containing switch and ENS cost along with system ENS is shown in Table 1 for the two risk levels.
Final results including number of manual and automatic switches, investment cost and system ENS both in defuzzificated form are given in Table 2 and location of switches in the network is shown in Table 3. Comparing the results, it can be seen that by lowering the risk related to load transfer, there is rise in switch cost while the system ENS is reduced. It seems to be true to reduce the risk of incorrect load transfer; location and number of switches must change.
Also, the results of Table 3 related to the location of manual and automatic switches are demonstrated in Figures 6 and 7 for the two risk levels.
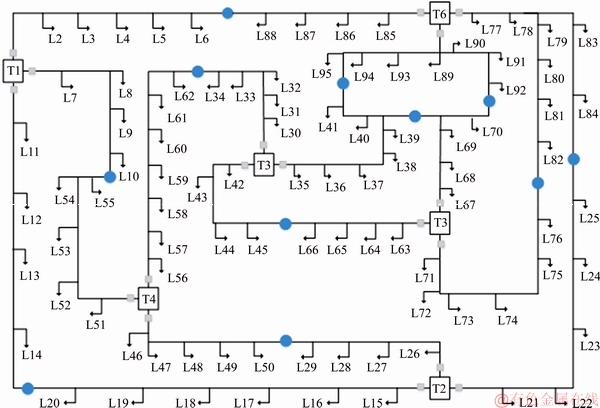
Figure 5 95-bus network schematic
Table 1 Fuzzy cost and system ENS for scenario 1

Table 2 Output results for scenario 1

Table 3 Switch location for scenario 1

3.2 Scenario 2: Load importance based switch placement
The planning strategy is revised in this scenario. Based on the load importance concept, a multi-objective switch placement is applied by prioritizing the loads. Buses L={17, 19, 73, 74, 79, 80, 81} are considered critical loads with the same degree of importance.
With respect to the aforementioned constraints, only the ENS of these loads is considered in total investment cost. It is aimed to minimize the investment cost by reducing the total risk associated with violation of constraints. In addition, the total ENS of system must not exceed the amount 0.36 MW·h. To have a better evaluation, the fuzzy optimization is performed just for the LT risk of 5% and the LT risk of 30% is neglected. Figure 8 demonstrates the Pareto frontier in which by reduction in investment cost, the risk increases. Using fuzzy decision method, the best point is selected through the non-dominatedsolutions.
Total cost and system ENS as TFN for this scenario are shown in Table 4. As it is apparent, the risk of exceeding permissible value for system ENS is zero. After defuzzification, total cost and ENS are 82044 $ and 328880 kW·h, respectively. Furthermore, the system ENS is under the maximum permissible value with the risk of about 7% that seems to be a low percentage. Table 5 represents the location of manual and automatic switches. Finally, the fuzzy ENS of load set L in both scenarios is given in Table 6.
By adopting the load importance based strategy for switch placement, ENS of these load points must not exceed the values obtained in scenario 1. In this regard, the last column shows the risk of ENS rise for them.
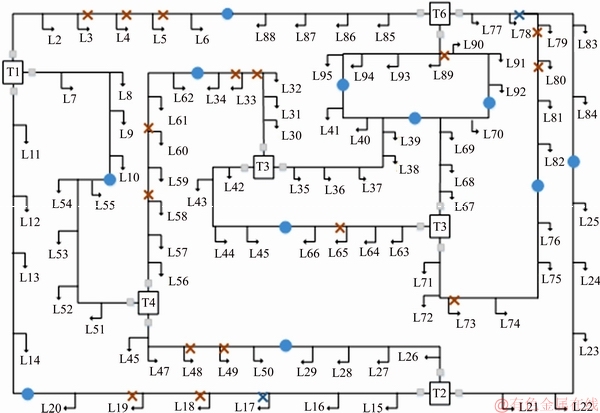
Figure 6 Location of switches for RLT=5% (Red crosses: Manual switch, blue crosses: Automatic switch)
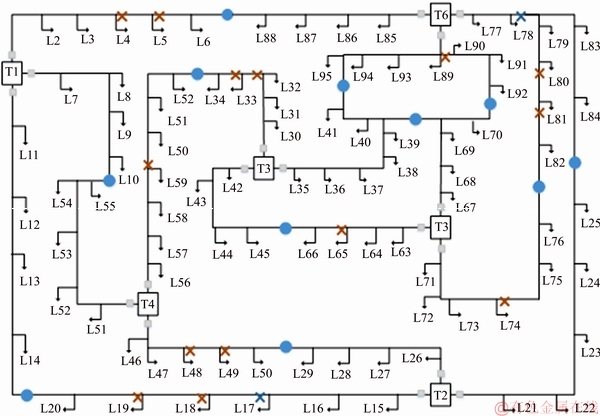
Figure 7 Location of switches for RLT=30% (Red crosses: manual switch; Blue crosses: automatic switch)
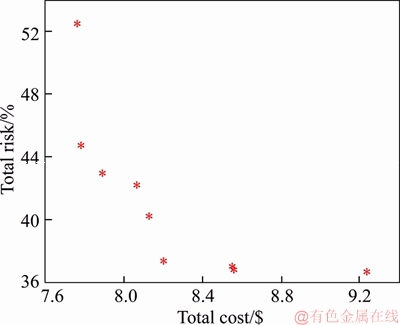
Figure 8 Pareto solutions for second scenario
Table 4 TFN results of total cost and system ENS for second scenario represented as TFN

Table 5 Switch location for scenario 2

According to the abovementioned results and comparison with previous scenario, switch cost as a certain payment has considerable drop which provides benefit for DISCO.
Table 6 Fuzzy ENS of critical loads in both scenarios and the risk of ENS exceeding for these customers
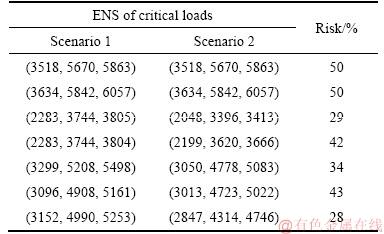
Furthermore, the risks associated with ENS rise of either system or critical load point are in an acceptable level for decision maker. This serves the goal of DISCO in investment cost reduction through the asset management strategy.
It must be noticed that in conventional switch placement as the first strategy, the switches are almost uniformly distributed in the network to reduce the total ENS of system. However, by adopting the new strategy in second scenario, the planner has succeeded to reduce the switch cost. These switches have been allocated in a way to effect on total ENS of critical customers from the DISCO viewpoint. Also most of the switches are allocated in feeders that contain critical loads.
Despite the reduction in switch cost, total system ENS over the planning horizon has increased but not in an extent that leads to a substantial reliability attenuation in the network. These accomplishments are obtained by employing the risk management which is permitted to properly handle the associated risks.
4 Conclusions
This paper introduced a novel fuzzy switch placement strategy in the context of asset management policies that can be profitable for DISCOs. Unlike the conventional switch placement, this kind of planning is based on load importance and just considers the ENS of critical loads instead of whole load points in the network. Also, to evaluate the effectiveness of the proposed strategy, a conventional switch placement was assessed too. Due to the uncertainties inherent in distribution system, fuzzy set theory was implemented to model the objective functions and their associated constraints.
It was observed that employment of this strategy is profitable for DISCO from the economical perspective due to the considerable reduction in switch cost relative to the conventional planning. Furthermore, comparing the conventional planning, total ENS of critical customers from the DISCO viewpoint had an acceptable reduction.
What was important here is that the ENS of each critical customer had an increase relative to the obtained value in conventional planning within an acceptable risk. In addition, the system ENS was held below the permissible level with a low risk of violation. Another remarkable point is that the new defined switching mechanism in the fuzzy environment of system had a direct effect on the planning results and depending on LT risk level parameter, switch number and location and consequently the reliability was changed.
References
[1] TOR O, SHAHIDEHPOUR M. Power distribution asset management [C]// IEEE Power Engineering Society General Meeting. Montreal: IEEE, 2006: 1–7.
[2] NORDG RD D E. A framework for risk-informed decision support in electricity distribution companies utilizing input from quantitative risk assessment [J]. Electrical Power and Energy Systems, 2012, 43(1): 255–261.
RD D E. A framework for risk-informed decision support in electricity distribution companies utilizing input from quantitative risk assessment [J]. Electrical Power and Energy Systems, 2012, 43(1): 255–261.
[3] DEHGHANIAN P, FOTUHI M, SHOURAKI S B, KAZEMI A. Critical component identification in reliability centered asset management of power distribution systems via fuzzy AHP [J]. IEEE Systems Journal, 2012, 6(4): 593–602.
[4] MORADKHANI A, HAGHIFAM M R, MOHAMMADZADEH M. Failure ratemodelling of electric distribution overhead lines considering preventive maintenance [J]. IET Gen, Trans & Distr, 2013, 8(6): 1028–1038.
[5] CATRINU M D, NORDG RD D E. Integrating risk analysis and multi-criteria decision support under uncertainty in electricity distribution system asset management [J]. Reliability Engineering and System Safety, 2011, 96(6): 663–670.
RD D E. Integrating risk analysis and multi-criteria decision support under uncertainty in electricity distribution system asset management [J]. Reliability Engineering and System Safety, 2011, 96(6): 663–670.
[6] BILLINTON R, JONNAVITHULA S. Optimal switching device placement in radial distribution systems [J]. IEEE Trans Power Delivery, 1996, 11(3): 1646–1651.
[7] ABIRI-JAHROMI A, FOTUHI M, PARVANIA M, MOSLEH M. Optimized sectionalizing switch placement strategy in distribution systems [J]. IEEE Trans Power Delivery, 2012, 27(1): 362–370.
[8] XU Y, LIU C, SCHNEIDER KEVIN P, TON DAN T. Placement of remote-controlled switches toenhance distribution system restoration capability [J]. IEEE Transactions Power Systems, 2016, 31(2): 362–370.
[9] SILVA L, GONZALEZ J F, USBERTY F, LYRA C, CAVELLUCCI C, ZOBEN V. Switch allocation problems in power distribution systems [J]. IEEE Trans Power Syst, 2014, 30(1): 246–253.
[10] SHAHSAVARI A, FEREIDUNIAN A, MAZHARI S M. A joint automatic and manual switch placement within distribution systems considering operational probabilities of control sequences [J]. Int Tran Electr Energ Syst, 2015, 25(11): 2745–2768.
[11] BEZERRA J R, BARROSO G, LEAO R, SAMPIO R. Multiobjective optimization algorithm for switch placement in radial power distribution networks [J]. IEEE Trans Power Delivery, 2015, 30(2): 545–552.
[12] SARDOU G, BANEJAD M, HOOSHMAND R, DASTFAN A. Modified shuffled frog leaping algorithm for optimal switch placement in distribution automation system using a multi-objective fuzzy approach [J]. IET Gen Trans & Dist, 2012, 6(6): 493–502.
[13] FALAGHI H, HAGHFAM M R, SINGH C. Ant colony optimization-based method for placement of sectionalizing switches in distribution networks using a fuzzy multiobjective approach [J]. IEEE Trans on Power Delivery, 2009, 24(1): 268–276.
[14] SAMADI F, SALEHI J. Stochastic multi-objective framework for optimal dynamic planning of interconnected microgrids [J]. IET Renewable Power Generation, 2017, 11(14): 1749–1759.
[15] POMBO A, PINA J, PIRES V. Multiobjective planning of distribution networks incorperating switches and protective devices using a memetic optimization [J]. Reliability Engineering & System Safety, 2015, 136: 101–108.
[16] MAZIDI M R, AGHAZADEH M, TESHNIZI Y, MOHAGHEGHI E. Optimal placement of switching devices in distribution networks using multi-objective genetic algorithm NSGA-II [C]// Electrical Engineering (ICEE). Iranian Conference. Mashhad, Iran, 2013.
[17] ROSADO I, ALBA E. Optimizing the number and location of switching devices in power distribution networks [C]// Advances in Mechanical and Electronic Engineering. 2013: 309–316.
[18] MAZHARI S M, MONSEF H, ROMERO R. Ahybrid heuristic and evolutionary algorithm for distribution substation planning [J]. IEEE Systems Journal, 2015, 9(4): 1396–1408.
[19] GITIZADEH M, VAHED A, AGHAEI J. Multistage distribution system expansion planning considering distributed generation using hybrid evolutionary algorithms [J]. Applied Energy, 2013, 101: 655–656.
[20] POPOVICH DRAGAN S, POPOVICH ZELJKO N. A risk management procedure for supply restoration in distribution networks [J]. IEEE Trans Power Syst, 2004, 19(1): 221–228.
[21] NAZARKO J, ZALEWSKI W. The fuzzy regression approach to peak load estimation in power distribution systems [J]. IEEE Trans Power Syst, 1999, 14(3): 809–814.
[22] RAMIREZ-ROSADO I J, DOMIGEZ-NAVARO J A. Possibilistic modelbased on fuzzy sets for the multiobjective optimal planning of electric power distribution networks [J]. IEEE Trans Power Syst, 2004, 19(4): 1801–1810.
[23] SHYAMAL A K, PAL M. Triangualr fuzzy matrices [J]. Iranian Journal of Fyzzy Systems, 2007, 4(1): 75–87.
[24] LI W, ZHOU J, XIE K, XIONG X. Power system risk assessment using a hybrid method of fuzzy set and Monte Carlo simulation [J]. IEEE Transaction on Power Sys, 2008, 23(2): 336–343.
[25] BORTOLAN G, DEGANI R. A review of some methods for ranking fuzzy subsets [J]. Fuzzy Sets and Systems, 1985, 15(1): 1–19.
[26] FORTEMPS P, ROUBENS M. Ranking and defuzzication methods based on area compensation [J]. Fuzzy Sets and Systems, 1996, 82(3): 319–330.
[27] KHADEMI N, BAHAABADI M R, MOHAYMANY A S, SHAHI J. Deriving fuzzy inequalities using discreteapproximation of fuzzy numbers [J]. International Journal of Industerial Engineering & Production Research, 2013, 24(3): 207–216.
[28] TSENG Y, KLEIN C M. New algorithm for the ranking procedure in fuzzy decsion making [J]. IEEE Trans Power Syst, 1989, 19(5): 1289–1296.
[29] BOOKSTEIN A, KULYUKIN V, RAITA T. Generalized hamming distance [J]. Information Retrieval, 2002, 5(4): 353–375.
[30] MOHAMMADI M, ABASI M, ROZBAHANI A M. Fuzzy-GA based algorithm for optimal placement and sizing of distribution static compensator (DSTATCOM) for loss reduction of distribution network considering reconfiguration [J]. Journal of Central South University, 2017, 24(2): 245- 258.
[31] MOHAMMADI M, ROZBAHANI A M, BAHMANYAR S. Power loss reduction of distribution systems using BFO based optimal reconfiguration along with DG and shunt capacitor placement simultaneously in fuzzy framework [J]. Journal of Central South University, 2017, 24(1): 90-103.
[32] DEB K, AGRAWAL S, PRATAB A. A fast and elisit multiobjective genetic NSGA-II [J]. IEEE Trans Evolutionay Computation, 2002, 6(2): 182–197.
[33] ZANGENEH A, JADID S, RAHIMI-KIAN A. A fuzzy environmental-technical-economic model for distributed generation planning [J]. Energy, 2011, 36(5): 3437–3445.
[34] WANG L, SINGH C. Environmental/economic power dispatch using a fuzzified multi-objective particle swarm optimization algorithm [J]. Elect Power Syst Res, 2007, 77(1): 1654–1664.
[35] YIN S, LUE C N. Distribution feeder scheduling considering variable load profile and outage cost [J]. IEEE Trans Power Syst, 2009, 24(2): 652–660.
(Edited by YANG Hua)
中文导读
考虑资产管理原则的提高配电网自动化水平的模糊切换优化配置
摘要:由于配电部门固有的大量故障,配电公司负责达到一个可接受的可靠性指标;否则,他们将面临投诉。因此,监管机构通常有义务对网络的可靠性改进进行投资,但对可靠性的投资通常是从配电公司的角度出发的,而与顾客满意度无关。一方面,用户对配电中断的敏感性是不相同的,若只提高网络的可靠性,而没有考虑到负载的重要程度和可靠性要求的差异;另一方面,配电公司试图尽可能地降低投资成本。本文从资产管理策略的角度,介绍了一种新的联合交换机配置方法,它可以降低交换机的成本。为此,在不同类型的策略中进行了两种开关布局规划,以比较它们的结果。首先,在减少系统未提供的总能量(ENS)的基础上执行开关控制。然后,通过修改策略,从配电公司的角度进行模糊开关布局,只考虑最敏感于被称为重要或临界负荷的中断的负载点的总数。此外,通过满足相关约束,忽视低敏感用户的可靠性。这是一种基于负荷重要性的规划,它可以相对于以往策略实现的切换成本降低,并意味着与可靠性和相应约束相关的风险管理。在模糊网络环境下,采用模糊方法和新的切换机制来建模和控制与临界负荷相关的风险,并对系统的风险进行建模和控制。
关键词:模糊切换布局;资产管理;配电公司;可靠性;负荷重要性规划
Received date: 2017-06-24; Accepted date: 2018-02-28
Corresponding author: JAVAD Salehi, PhD, Assistant Professor; Tel: +98-41-31452538; E-mail: j.salehi@azaruniv.ac.ir, salehi.azaruniv@gmail.com; ORCID: 0000-0002-8140-8301
Abstract: Since distribution sector is inherent into high amount of failures, distribution companies (DISCOs) are responsible of attaining an acceptable value for the reliability indices and otherwise they will face up to complaints. So they are usually obligated by regulators to invest on reliability improvement of network. But this investment on reliability is usually from the DISCO’s viewpoint and is also irrespective of customer satisfaction level. In other words, customers are not at the same level of sensitivity to interruptions but DISCO improves the reliability of network without considering the differences in importance degree of loads and their level of reliability requirement. On the other hand DISCOs attempt to reduce their investment costs as much as possible. This paper introduces a novel approach in the field of joint switch placement that can reduce the switch cost from the perspective of asset management policies. To this end, two switch placement plannings in different types of strategies are performed to compare their results. Firstly as witch placement is performed based on reducing the total energy not supplied (ENS) of the system. Then by revising the strategy, a fuzzy switch placement is performed from the DISCO’s point of view which just considers the total ENS of load points most sensitive to interruptions known as important or critical loads. Furthermore, by meeting the related constraints, the reliability of low sensitive customers is disregarded. This is a load importance based planning which can result in switch cost reduction relative to the amount achieved in previous strategy and implies the management of risks associated with reliability and respective constraint. Fuzzy method and new switching mechanism in fuzzy environment of network are implemented to modeling and controlling the risks associated to ENS of critical loads and also the ENS of system.


