J. Cent. South Univ. Technol. (2011) 18: 1773-1779
DOI: 10.1007/s11771-011-0901-5![]()
First-principles calculation of structural and
thermodynamic properties of titanium boride
LI Yan-feng(李燕峰)1, 2, XU Hui(徐慧)1, 2, XIA Qing-lin(夏庆林)1, LIU Xiao-liang(刘小良)1
1. School of Physical Science and Technology, Central South University, Changsha 410083, China;
2. School of Materials Science and Engineering, Central South University, Changsha 410083, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract:
The equilibrium lattice parameters, electronic structure, bulk modulus, Debye temperature, heat capacity and Gibbs energy of TiB and TiB2 were investigated using the pseudopotential plane-wave method based on density functional theory (DFT) and the improved quasi-harmonic Debye method. The results show that the total density of states (DOS) of TiB2 is mainly provided by the orbit hybridization of Ti-3d and B-2p states, and the total DOS of TiB is mainly provided by the hybrids bond of Ti-3d and B-2p below the Fermi level and Ti—Ti bond up to the Fermi level. The Ti—B hybrid bond in TiB2 is stronger than that in TiB. Finally, the enthalpy of formation at 0 K, heat capacity and Gibbs free energy of formation at various temperatures were determined. The calculated results are in excellent agreement with the available experimental data.
Key words:
1 Introduction
Titanium borides, including TiB and TiB2, are important members of the large family of transition metal–metalloid compounds possessing many unexpected properties and have been investigated extensively in many aspects [1]. Owing to their high strength and durability, the traditional applications of titanium borides are mainly limited to areas such as impact resistant armor, cutting tools and particulate reinforced steel [2]. However, since titanium borides can resist electron migration and prevent diffusion due to the strong interatomic bonding in them, there has been an upwelling of recent interest in further applications. Therefore, an increasing number of applications in thin-film interconnect and diffusion barriers in very large-scale integrated circuits [3] have been found at present. For example, in an important application recently evolved, titanium diboride has been used as a coating on particles in a bioactive glass-ceramic matrix designed for surgical implant materials [4].
The space groups of TiB and TiB2 are Pnma [5] and P6/mmm [6], respectively. As for their properties such as elastic modules, the result of ultrasonic pulse-echo measurements provides four elastic coefficients and an estimate for the value of C13. While the study based on resonant ultrasound spectroscopy [7] gives a very different set of elastic coefficients, with off-diagonal terms being one order of magnitude smaller than those previously reported, and the data are in noticeably better agreement with the results for polycrystals [8]. In a more recent theoretical study, PEROTTONI et al [9] evaluated the mechanical properties of TiB2 using the periodic Hartree–Fock (HF) method, but their results disagreed with the experimental data. MILMAN and WARREN [10] even thought that there were no reliable data either on static or shock compression of titanium diboride.
Besides many studies on the elastic properties of titanium boride, there are many studies on the electronic structure of titanium boride. HAN et al [1] studied the transition-metal diborides (TMDB) surfaces by first principle calculation and found that strong covalent B—B bonds exist between B atoms in the same layer and the Ti—B bonds form between the neighboring layers, which were observed in both theoretical and experimental works in bulk TiB2 [11-12]. There are two conflicting opinions on the electron transfer between B and Ti atoms, which are closely related to the chemical bonding between Ti and B layers [12-13]. Even in the field of thermodynamic properties, such as the entropy, the heat capacity and the enthalpy of titanium boride remain highly controversial [14].
The aim of this work is to give a comparative and complementary investigation on structural, thermo- dynamic and electronic properties of the Ti-B compounds using the plane-wave pseudopotential based on DFT method, and to understand the reaction mechanisms and thermo-dynamic properties of the material.
2 Theoretical methods
2.1 Electronic structure calculation
The pseudopotential plane-wave method based on DFT was applied to doing all the calculations. Broyden- Fcetcher-Goldfarb-Shanne (BFGS) algorithm was used to relax the crystal structures. In the electronic structure calculations, the ultra-soft pseudopotentials introduced by VANDERBILT [15] were employed with the generalized gradient approximation (GGA) proposed by PERDEW et al (PW91) [16] as an exchange-correlation function. A plane-wave basis set with an energy cut-off of 280 eV was applied. Pseudo-atomic calculations were performed for Ti 4s23d2 and B 2s22p1. For the Brillouin zone sampling, a 6×6×6 Monkhorst–Pack mesh was used in the calculation of ground state properties, while a 12×12×12 Monkhorst–Pack mesh was used in the band structure calculation. The self-consistent convergence of the total energy is 10-6 eV/atom. All these total-energy electronic structure calculations were carried out using the CASTEP code.
2.2 Thermodynamic properties
The quasi-harmonic Debye model was employed to calculate the equation of state (EOS) and the thermodynamic properties which are constructed from the Helmholtz free energy at the temperature below melting point in the quasi-harmonic approximation. This method was adapted for the investigation of thermo- dynamic properties [17], in which the non-equilibrium Gibbs function of the crystal phase G*(V, P, T) can be written in the form of [18]
G*(V, P, T)=E(V)+PV+Avib(V, T) (1)
where E(V) is the total energy per unit cell; PV corresponds to the constant hydrostatic pressure condition; Avib is the vibrational Helmholtz free energy, which can be written as
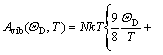
![]() (2)
(2)
where k is a constant; ΘD is the Debye temperature; N is the number of atoms per formula unit; and D(y) is the Debye integral defined as
![]() (3)
(3)
The Debye characteristic temperature of the solid, ΘD in Eq.(2) is related to an average sound velocity (vD), because in Debye’s theory the vibrations of the solid are considered as elastic waves. For an isotropic solid, ΘD can be computed as follows with Poisson ratio ![]() 0.25 [19]:
0.25 [19]:
 (4)
(4)
where kB, Bs, V and r are the Boltzman constant, the elastic modulus, volume of primitive cell and density, respectively.
In order to perform static optimizations for Eq.(1), an appropriate approximate algorithm was applied using the Gst(V, P)=Hst(V, P)=E(V)+PV. Then, after the static calculation, Eq.(1) can be rewritten as
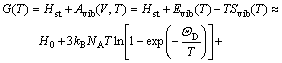
![]() (5)
(5)
where Evib(T) and Svib(T) are the vibrational internal energy and vibrational entropy, respectively; NA is the Avogadro constant. According to the quasi-harmonic Debye model, the heat capacity (cV) and vibrational entropy (Svib) can be obtained by
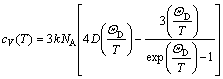 (6)
(6)
![]() (7)
(7)
here, in the approximate formula at low temperature, cV, low is given as follows:
![]() (8)
(8)
The calculation methods above are not computationally expensive, while the Debye temperature ΘD and Bs are all equal to the values of standard equilibrium state. Using the methods mentioned above, the elastic and thermodynamic properties of TiBx (x=1, 2) can be successfully obtained.
3 Results and discussion
3.1 Geometry, elastic constants and modulus
The lattice constants and mechanical constants for TiB after optimization are shown in Table 1. As listed in Table 1, the calculated lattice parameters for TiB are in excellent agreement with the previous experimental results and theoretical estimates.
For TiB2, it can be seen that previous theoretical estimates of the bulk modulus, based on the DFT approach [10] and experiment [7], are close to the results obtained in the present studies. However, a TB–LMTO study with the LDA predicts much larger cell parameters [11] and a correspondingly lower bulk modulus than any other theoretical work (Table 1). The error of the LMTO calculation is especially large, which reveals that the LMTO results are unreliable. It is thus unclear why the LDA results of the all-electron TB–LMTO calculations overestimate the cell volume to such a degree. The most likely reason is the general shortcoming of the LMTO techniques that does not contain a full-potential treatment.
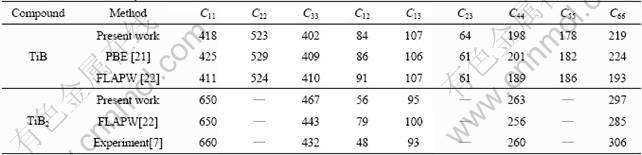
The calculated elastic constants for TiB and TiB2 are presented in Table 2, with values from previous theoretical and experimental works. The GGA calculation agrees well with this set of data except for C12 and C66 components. The error of the FLAPW calculation is especially larger than that of PBE method [21] in TiB and experimental data [7] in TiB2 for C12 and C66 components. The results of the present work thus strengthen the conclusion that the values of FLAPW [22] are erroneous. The consistency between the present calculations demonstrates that the bulk modulus calculated from the elastic constants in Table 2 agrees with the values derived from the previous theoretical and experimental data.
3.2 Electronic structure
The calculated electronic structures for the two compounds are displayed in Fig.1. It is clear that TiB and TiB2 exhibit metallic behavior. The curves of them (see Figs.1(a) and (c)) show clearly that there has a valley region (pseudo-gap) which can distinguish the high- energy anti-bonding states and low-energy bonding states, especially for TiB2. This pseudo-gap which manifests a typical stability effect was observed earlier by ROSNER et al [25]. The pseudo-gap in binary alloys is believed to be of ionic origin or come from the covalent hybridization [11]. However, ionicity does not contribute much to bonding here. The most popular opinion is that the pseudo-gap is due to the p—d σ bonding between B and Ti atoms. According to VAJEESTON et al [11], the pseudo-gap originates from strong covalent bonding between B atoms, i.e. from the B(p)—B(p) covalent contribution. ROSNER et al [25] pointed out that the pseudo-gap is due to the relatively large velocities in the region of Fermi level (EF) rather than any semi-metallic overlapping of bands.
Table 1 Lattice parameters and bulk modulus for TiB and TiB2
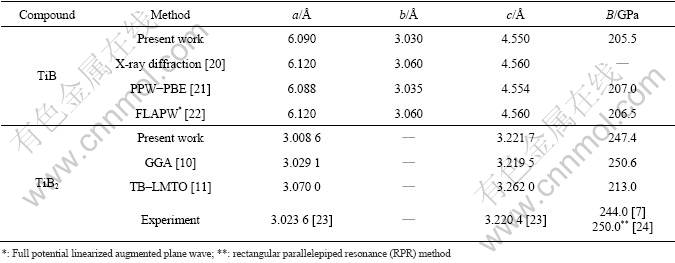
Table 2 Elastic constants Cij for TiB and TiB2 (GPa)
As can be seen from Fig.1, the DOSes of TiB and TiB2 consist of the hybrid bond of Ti-3d and B-2p below the Fermi level. In the vicinity of the Fermi level, the DOSes of TiB and TiB2 are mainly provided by the Ti-3d orbit. In the high-energy region above the Fermi level, the DOS of TiB consists of Ti—Ti bond, but the DOS of TiB2 is more complex which includes Ti—Ti, Ti—B and B—B bonds. Meanwhile, strong hybrid bond of Ti-3d and B-2p appears in the region above the Fermi level, which indicates that the Ti—B hybrid bond in TiB2 is greater than that of TiB. The conclusion is consistent with the views of PANDA and CHANDRAN [22, 26].
In addition, the band stretching of TiB2 (Fig.1(b)) is significantly wider than that of TiB (Fig.1(d)), and the valence band of TiB2 shows obvious parabolic shape and the feature of sp-like band. This indicates that the non-local level of the electrons as well as the covalence in TiB2 is greater. So, the differences in electronic structure determine that the elastic modulus of TiB2 is higher than that of TiB.
The present results of DOSes for TiB and TiB2 in Table 3 are almost consistent with the data from experiments and previous calculation. But the DOS at the Fermi level shows a remarkable discrepancy with the atomic sphere approximation (LMTO-ASA) method. This discrepancy appears to be caused by the lack of consideration of the electron-phonon interaction in the calculation. In the vicinity of the Fermi level, the DOS of TiB2 is lower than that of TiB, which indicates that TiB2 is poor metal, in contrast with the semiconducting property of the pyrite phase.
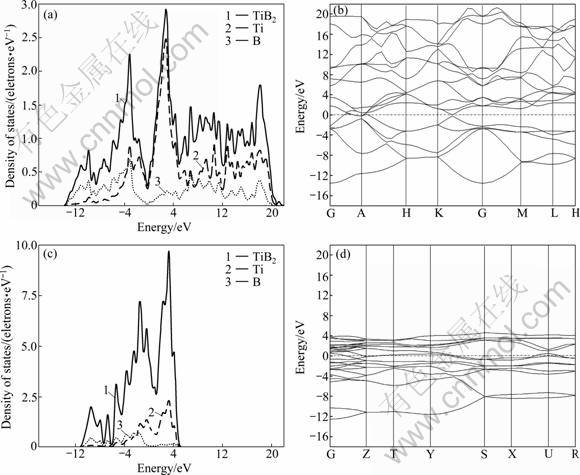
Fig.1 Electronic structure of TiB and TiB2: (a) Density of states of TiB2; (b) Band structure of TiB2; (c) Density of states of TiB; (d) Band structure of TiB
Table 3 Comparisons of present results with previous works

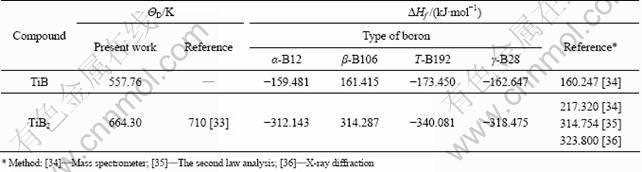
Table 4 Values of Debye temperature ΘD and enthalpy of formation ΔHf at 0 K
3.3 Thermodynamic properties of Ti-B compound
The Ti-B system has been assessed by MURRAY et al [29] and MA et al [14]. The thermodynamic data of TiB [30] and TiB2 [29] have already been given by many authors. But there are many disagreements and contradictories among these literatures on the thermodynamic data, such as melting temperature and compound solution phases [14].
The simplified quasi-harmonic Debye model empowers us to obtain the enthalpy ΔHf, Debye temperature ΘD, heat capacity cV and the Gibbs free energy of formation. The calculated Debye temperature ΘD and enthalpy of formation at 0 K of the two intermetallic compounds are illustrated in Table 4. For pure boron, which is one of the most enigmatic elements [31], there are at least sixteen kinds of known polymorphs, and most of them are not yet experimentally established even at ambient conditions. Boron is known to exist in four pure phases at present, i.e. rhombohedral α-B12, β-B106, tetragonal T-B192 and orthorhombic γ-B28 [32], and γ-B28 is the newly synthesized high- pressure phase of boron.
The calculated value of ΘD is a little smaller than Bloch-Gruneisun parameters [33]. For the enthalpy of formation, the four boron phases including the latest one [32] are considered and the calculated values are in conformity with the literatures.
The calculated relationship between heat capacities and temperatures at standard pressure is plotted in Fig.2. It is clear that when the temperature is below 300 K, the heat capacity is strongly dependent on temperature and increases rapidly with temperature increasing, which is due to the anharmonic approximation of the Debye approximation used here. However, the anharmonic effect on heat capacity is suppressed when the temperature is above 300 K. Heat capacity is very close to the Dulong–Petit limit, which is common to all solids at high temperatures. These results show the fact that the interactions between ions in TiB and TiB2 have great effect on the heat capacity especially at low temperatures. Unfortunately, there are no theoretical results or experimental data to check the calculated results.
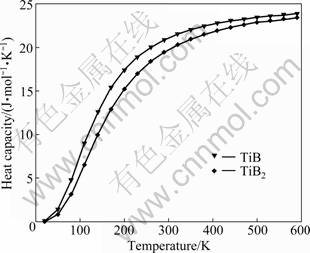
Fig.2 Relationship between heat capacities and temperatures at standard pressure
The zero-pressure Gibbs free energy of formation for the reaction (solid-solution phase) can also be calculated using the following relation:
Ti+B=TiB (9)
Ti+2B=TiB2 (10)
The calculated Gibbs free energies of formation at zero-pressure together with the literature data [37] are given in Fig 3. It shows the comparison of the calculated phase diagram with the experimental data. Satisfactory agreement is obtained. The temperature differences of all the invariant reactions between the thermodynamic prediction and the practical measurement are within experimental error.
As can be seen from Fig.3, the reaction of TiB2 is easier than that of TiB. The Gibbs free energies of formation of them are negative, and the data of TiB2 are smaller than these of TiB, which indicates that TiB2 is of priority to be generated in Ti-B reaction. One thing needs to be noted is that although the TiB2 is easier to be generated than TiB in thermodynamic, the diffusion coefficient of boron in TiB2 to the titanium matrix and the growth rate of TiB is very high, which causes the real product is TiB, rather than TiB2.
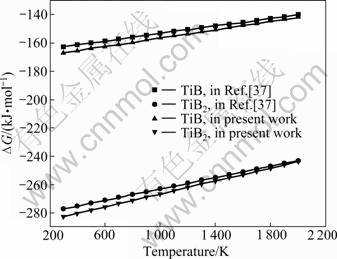
Fig.3 Variations of ΔG with temperature for reactions
4 Conclusions
1) The calculated lattice parameters and mechanical constants for TiB are in excellent agreement with the previous experiment and theoretical estimates, except for C12 and C66 components. The errors of TB-LMTO-LDA in cell parameters and the FLAPW in elastic constants especially are large and the results are unreliable.
2) The DOSes of TiB and TiB2 consist of the hybrid bonds of Ti-3d and B-2p below the Fermi level and Ti—Ti 3d orbit in the vicinity of the Fermi level. In the high-energy region up to the Fermi level, the Ti—B hybrid bond in TiB2 is stronger than that in TiB. The band stretching indicates that the non-local level of the electrons as well as the covalence in TiB2 is greater.
3) The value of EF indicates that the GGA method is appropriate to calculate the DOS of TiB. The calculated values of Debye temperature and the enthalpy of formation at 0 K are in good agreement with the experience considering the four boron phases. These estimated data are used to predict the Gibbs energy and the heat capacities. The values of Gibbs free energy of formation and heat capacities at zero-pressure in variation temperatures are calculated, the differences between calculated values and the experimental data are within experimental error.
References
[1] HAN Yan-feng, DAI Yong-bing, SHU Da, WANG Jun, SUN Bao-de. First-principles study of TiB2(0001) surfaces [J]. Journal of Physics: Condensed Matter, 2006, 18(17): 4197-4205.
[2] WANG Hui-yuan, JIANG Qi-chuan, ZHAO Yu-guang, ZHAO Fang. In situ synthesis of TiB2/Mg composite by self-propagating high- temperature synthesis reaction of the Al-Ti-B system in molten magnesium [J]. Journal of Alloys and Compounds, 2004, 379(1): 4-7.
[3] PELLEG J. Schottky barrier formation at Al/TiB2/TiSi2/Si and Cu/TiB2/TiSi2/Si interfaces [J]. Microelectronic Engineering, 2004, 75(4): 413-422.
[4] CHOY K L, BALZER R, RAWLINGS R D. Diffusion barrier coatings on ductile particles for protection in bioactive glass-ceramic matrix [J]. Journal of the European Ceramic Society, 2000, 20(12): 2199-2207.
[5] DECKER B F, KASPER J S. The crystal structure of Ti-B [J]. Acta Crystallographica, 1954, 7(1): 77-81.
[6] HEGENSCHEIDT T. Possibilities and limits of roentgen-diffraction experiments demonstrated using the example of three “simple” structures [D]. Karlsruhe, Germany. Department of Physics, University of Karlsruhe. 1998: 1-81.
[7] SPOOR P S, MAYNARD J D, PAN M J, GREEN D J, HELLMANN J R, TANAKA T. Elastic constants and crystal anisotropy of titanium diboride [J]. Applied Physics Letters, 1997, 70(15): 1959-1961.
[8] WRIGHT S I. Estimation of single-crystal elastic constants from textured polycrystal measurements [J]. Journal of Applied Crystallography, 1994, 27(5): 794-801.
[9] PEROTTONI C A, PEREIRA A S, JORNADA J A H. Periodic Hartree-Fock linear combination of crystalline orbitals calculation of the structure, equation of state and elastic properties of titanium diboride [J]. Journal of Physics: Condensed Matter, 2000, 12(32): 7205-7222.
[10] MILMAN V, WARREN M C. Elastic properties of TiB2 and MgB2 [J]. Journal of Physics: Condensed Matter, 2001, 13(24): 5585-5595.
[11] VAJEESTON P, RAVINDRAN P, RAVI C, ASOKAMANI R. Electronic structure, bonding, and ground-state properties of AlB2-type transition-metal diborides [J]. Physical Review B, 2001, 63(4): 045115-045127.
[12] LIE K, BRYDSON R, DAVOCK H. Band structure of TiB2: Orientation-dependent EELS near-edge fine structure and the effect of the core hole at the B//K edge [J]. Physical Review B, 1999, 59(8): 5361-5367.
[13] LIE K, HOIER R, BRYDSON R. Theoretical site- and symmetry- resolved density of states and experimental EELS near-edge spectra of AlB2 and TiB2 [J]. Physical Review B, 2000, 61(3): 1786-1794.
[14] MA Xiao-yan, LI Chang-rong, DU Zhen-min, ZHANG Wei-jing. Thermodynamic assessment of the Ti-B system [J]. Journal of Alloys and Compounds, 2004, 370(1): 149-158.
[15] VANDERBILT D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism [J]. Physical Review B, 1990, 41(11): 7892-7895.
[16] PERDEW J P, CHEVARY J A, VOSKO S H, KOBLAR A J, MARK R P, SINGH D J, CARLOS F. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation [J]. Physical Review B, 1992, 46(11): 6671-6687.
[17] WANG Hai-yan, CHEN Xiang-rong, ZHU Wen-jun, CHENG Yan. Structural and elastic properties of MgB2 under high pressure [J]. Physical Review B, 2005, 72(17): 172502-172506.
[18] BLANCO M A, FRANCISCO E, LUANA V. Gibbs: Isothermal- isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model [J]. Computer Physics Communications, 2004, 158(1): 57-72.
[19] ZHANG Wei, CHENG Yan, ZHU Jun, CHEN Xiang-rong. Structural, thermodynamic and electronic properties of zinc-blende AlN from ?rst-principles calculations [J]. Chinese Physics B, 2009, 18(3): 1207-1214.
[20] LI Feng-ying, CHEN Liang-chen, WANG Li-jun, GU Hui-cheng, WANG Ru-ju, CHE Rong-zheng, SHEN Zhong-yi. Pressure induced phase transition in TiB [J]. CHIN PHYS LETT, 2001, 18(9): 1240- 1241.
[21] YAO Qiang, XING Hui, MENG Li-Jun, SUN Jian. Theoretical calculation of elastic properties of TiB2 and TiB [J]. Chinese Journal of Nonferrous Metals, 2007, 17(8): 1297-1301. (in Chinese)
[22] PANDA K B, CHANDRAN K S R. First principles determination of elastic constants and chemical bonding of titanium boride (TiB) on the basis of density functional theory [J]. Acta Materialia, 2006, 54(6): 1641-1657.
[23] MUNRO R G. Material properties of titanium diboride [J]. Journal of Research of the National Institute of Standards and Technology, 2000, 105(5): 709-720.
[24] NORIHIKO L, OKAMOTO, KUSAKARI M, TANAKA K, INUI H, OTANI S. Anisotropic elastic constants and thermal expansivities in monocrystal CrB2, TiB2, and ZrB2 [J]. Acta Materialia, 2010, 58(1): 76-84.
[25] ROSNER H, AN J M, PICKETT W E, DRECHSLER S L. Fermi surfaces of diborides: MgB2 and ZrB2 [J]. Physical Review B, 2002, 66(2): 024521-024527.
[26] PANDA K B, CHANDRAN K S R. Determination of elastic constants of titanium diboride (TiB2) from first principles using FLAPW implementation of the density functional theory [J]. Computational Materials Science, 2006, 35(2): 134-150.
[27] TIAN De-cheng, WANG Xiao-bing. Electronic structure and equation of state of TiB2 [J]. Journal of Physics: Condensed Matter, 1992, 4(45): 8765-8772.
[28] IHARA H, HIRABAYASHI M, NAKAGAWA H. Band structure and X-ray photoelectron spectrum of ZrB2 [J]. Physical Review, 1977, 16(2): 726-730.
[29] MURRAY J L, LIAO P K, SPEAR K E. The B-Ti (boron-titanium) system [J]. Journal of Phase Equilibria, 1986, 7(6): 550-555.
[30] RUDY E, WINDISCH S. Ternary phase equilibria in transition metal–boron–carbon–silicon systems (Part I) [R]. Ohio: Air Force Materials Laboratory, Wright Patterson Air Force Base, 1966..
[31] JIANG Chao, LIN Zhi-jun, ZHANG Jian-zhong, ZHAO Yu-sheng. First-principles prediction of mechanical properties of gamma-boron [J]. Applied Physics Letters, 2009, 94(19): 191906-191911.
[32] OGANOV A R, CHEN J, GATTI C, MA Y Z, MA Y M, GLASS C W, LIU Z X, YU T, KURAKEVYCH O O, SOLOZHENKO V L. Ionic high-pressure form of elemental boron [J]. Nature, 2009, 457(7225): 863-867.
[33] WILLIAMS R K, BECHER P F, FINCH C B. Study of the Kondo effect and intrinsic electrical conduction in titanium diboride [J]. Journal of Applied Physics, 1984, 56(8): 202295-202303.
[34] SCHISSEL P O, TRULSON O C.Mass spectrometric study of the vaporization of the titanium-boron system [J]. Journal of Physical Chemistry, 1962, 66(8): 1492-1496.
[35] YURICK J, SPEAR K E. Thermodynamics of TiB2 from Ti-B-N studies [J]. Thermodynamics of Nuclear Materials, 1980, I: 73-90.
[36] GUZMAN L, ELENA A, MIOTELLO P M, OSSI D C, KOTHARI M. Phase formation in the N-B-Ti system [J]. Vacuum, 1995, 46(8): 951-954.
[37] LI Bang-sheng, WU Shi-ping, SHANG Jun-ling, GUO Jing-jie, FU Heng-zhi. Thermodynamics and dynamics of TiB formation in in-situ titanium matrix composite [J]. Aerospace Materials & Technology, 2005, 35(4): 42-46. (in Chinese)
(Edited by HE Yun-bin)
Foundation item: Project(07JJ3102) supported by the Natural Science Foundation of Hunan Province, China; Project(k0902132-11) supported by the Changsha Municipal Science and Technology, China
Received date: 2010-09-16; Accepted date: 2011-04-11
Corresponding author: XU Hui, Professor, PhD; Tel: +86-731-88836142; E-mail: xuhui@mail.csu.edu.cn
Abstract: The equilibrium lattice parameters, electronic structure, bulk modulus, Debye temperature, heat capacity and Gibbs energy of TiB and TiB2 were investigated using the pseudopotential plane-wave method based on density functional theory (DFT) and the improved quasi-harmonic Debye method. The results show that the total density of states (DOS) of TiB2 is mainly provided by the orbit hybridization of Ti-3d and B-2p states, and the total DOS of TiB is mainly provided by the hybrids bond of Ti-3d and B-2p below the Fermi level and Ti—Ti bond up to the Fermi level. The Ti—B hybrid bond in TiB2 is stronger than that in TiB. Finally, the enthalpy of formation at 0 K, heat capacity and Gibbs free energy of formation at various temperatures were determined. The calculated results are in excellent agreement with the available experimental data.


