J. Cent. South Univ. (2021) 28: 1843-1856

DOI: https://doi.org/10.1007/s11771-021-4734-6

AE waveform characteristics of rock mass under uniaxial loading based on Hilbert-Huang transform

LI Xue-long(李学龙)^{1, 2, 3, 4}, CHEN Shao-jie(陈绍杰)^{1, 3}, LIU Shu-min(刘淑敏)⁴, LI Zhong-hui(李忠辉)²

1. Mine Disaster Prevention and Control-Ministry of State Key Laboratory Breeding Base,

Shandong University of Science and Technology, Qingdao 266590, China;

2. State Key Laboratory of Coal Resources and Safe Mining, China University of Mining and Technology, Xuzhou 221116, China;

3. College of Energy and Mining Engineering, Shandong University of Science and Technology,Qingdao 266590, China;

4. State Key Laboratory of Coal Mine Disaster Dynamics and Control, College of Resource and Safety Engineering, Chongqing University, Chongqing 400030, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021

Abstract:

Acoustic Emission (AE) waveforms contain information on microscopic structural features that can be related with damage of coal rock masses. In this paper, the Hilbert-Huang transform (HHT) method is used to obtain detailed structural characteristics of coal rock masses associated with damage, at different loading stages, from the analyses of the characteristics of AE waveforms. The results show that the HHT method can be used to decompose the target waveform into multiple intrinsic mode function (IMF) components, with the energy mainly concentrated in the c₁-c₄ IMF components, where the c₁ component has the highest frequency and the largest amount of energy. As the loading continues, the proportion of energy occupied by the low-frequency IMF component shows an increasing trend. In the initial compaction stage, the Hilbert marginal spectrum is mainly concentrated in the low frequency range of 0-40 kHz. The plastic deformation stage is associated to energy accumulation in the frequency range of 0-25 kHz and 200-350 kHz, while the instability damage stage is mainly concentrated in the frequency range of 0-25 kHz. At 20 kHz, the instability damage reaches its maximum value. There is a relatively clear instantaneous energy peak at each stage, albeit being more distinct at the beginning and at the end of the compaction phase. Since the effective duration of the waveform is short, its resulting energy is small, and so there is a relatively high value from the instantaneous energy peak. The waveform lasts a relatively long time after the peak that coincides with failure, which is the period where the waveform reaches its maximum energy level. The Hilbert three-dimensional energy spectrum is generally zero in the region where the real energy is zero. In addition, its energy spectrum is intermittent rather than continuous. It is therefore consistent with the characteristics of the several dynamic ranges mentioned above, and it indicates more clearly the low-frequency energy concentration in the critical stage of instability failure. This study well reflects the response law of geophysical signals in the process of coal rock instability and failure, providing a basis for monitoring coal rock dynamic disasters.

Key words:

acoustic emission; waveform; Hilbert-Huang transform; coal rock；

Cite this article as:

LI Xue-long, CHEN Shao-jie, LIU Shu-min, LI Zhong-hui. AE waveform characteristics of rock mass under uniaxial loading based on Hilbert-Huang transform [J]. Journal of Central South University, 2021, 28(6): 1843-1856.

1 Introduction

At present, the methods for acoustic emission (AE) processing can be divided into two categories. One is the parameter analysis method, which is mainly used to characterize the signal by obtaining the ringing count, energy, amplitude, rise time, and locating the source of the AE signal [1-8]. The other is the waveform analysis method. The waveform of the AE signal contains a large amount of information about the fracture of the coal rock mass and the propagation medium of the signal. The waveform analysis of the AE signal can convey the source information regarding the fracture of the coal rock mass comprehensively and intuitively [9-14]. Therefore, in-depth study of the AE waveform characteristics concerning the process of coal rock mass post-peak failure is one of the possible ways to address the issue of the short-term warning associated with post-peak failure of fractured coal rock.

Spectrum analysis is the most common and basic method of waveform analysis [15-19]. The original waveform acquired with the AE device is a discrete time-varying non-linear signal, that is, a time-domain waveform signal. The spectrum analysis consists of converting these signals from a time domain representation into a frequency domain representation [20-22]. Unlike with the waveform signal analysis in the time and space domains, the frequency-domain analysis produces results that have the characteristic of being intrinsic and unique, thus reflecting the signal’s global spectral characteristics [23]. Scholars have studied the AE spectral characteristics of coal rock masses and have achieved many useful results. HE et al [24] conducted frequency-spectra analyses of AE signals from unloading rock burst tests on rectangular prismatic limestone specimens and found that there are much higher amplitude and lower frequency AE hits near the bursting failure.

Fourier transform is a simple frequency-domain analysis method, which is only able to determine the overall frequency-domain characteristics of the entire signal. It is limited by the Heisenberg uncertainty principle [25-27], where the time and frequency resolutions cannot be simultaneously arbitrarily small. In other words, there is a localized contradiction between the time domain and the frequency domain. To address this issue, the wavelet analysis method emerged, which can not only suppress the random interference of the signal but also decompose the signal at different scales by selecting different wavelet bases. Subsequently, the signals on each frequency band energy level are studied, and the dominant frequencies in each frequency band can be effectively found, thereby extracting as much useful information as possible [28-32]. For the low frequency component of the signal, a wide time window can be employed to reduce the time domain resolution and increase the frequency resolution. And for the high frequency part of the signal, a narrow time window can be employed to render a high time domain resolution and a low frequency domain resolution. For example, JEONG et al [33] used the lead-breaking test of graphite epoxy composite material to simulate the bending waveform signal and used Gabor wavelet transform to analyze the time-frequency intensity of the AE signal, indicating that the maximum intensity position corresponds to the signal in the three-dimensional image, thereby locating the precise position of the AE source. DING et al [34] used the wavelet packet transform method to study the acoustic source’s localization. It is pointed out that, in complex or small structures, the signal can easily change due to waveform reflection and mode alteration during propagation which determines the arrival time of the waveform.

Wavelet transform, an intrinsically window adjustable Fourier transform, is still limited by the Heisenberg uncertainty principle, thus requiring that the signal should be linear. In addition, the finite length of the wavelet base can cause energy leakage, and the choice of different wavelet basis functions to analyze the same signal can result in a large gap [35-38]. HUANG et al [39] proposed a new waveform analysis method, the Hilbert-Huang transform (HHT) method, as a spectral analysis method suitable for analyzing non-stationary signals and representing non-linear structures. HHT based on empirical mode decomposition (EMD) can not only uniquely decompose the signal, but also have good localization properties in the time domain and frequency domain [39-41]. Compared with Fourier transform, HHT can deal with non-stationary and transient problems. Compared with wavelet transform, HHT avoids the issues associated with the selection of basis functions and can distinguish high-frequency signals from low-frequency signals. This method has many other advantages [42-44]:1) Using no prior basis, so it is adaptive; 2) The EMD method is the best way to extract the signal trend and mean, and can well handle strong intermittent signals; 3) The instantaneous frequency obtained by Hilbert transform has clear physical meaning and can characterize the signal’s local features; 4) The three-dimensional energy spectrum obtained by HHT can accurately reflect the non-linear transformation characteristics of the system through the intra-wave modulation mechanism. Due to the above advantages, the HHT method had many successful application examples in seismic engineering, blasting vibration analysis, signal filtering, seismic liquefaction analysis, marine research, structural energy response analysis, and shaking table model test of concrete frame structure [45-54], showing excellent performance of the HHT method for non-stationary signal analysis.

Although the characteristics of AE resulting from the uniaxial loading process of coal rock masses have been studied substantially, the transient characteristics of AE waveforms for different loading stages haven’t been studied extensively. In this paper, we intend to use the HHT method to analyze the AE waveform characteristics during the entire loading process, so as to obtain more detailed structural characteristics of coal rock instability, thus reflecting the subtle changes of the coal rock structures more extensively. Additionally, it is expected to determine the response law of geophysical signals regarding the process of coal rock failure, so as to provide new reference support for better monitoring and warning of coal rock dynamic disasters.

2 Experimental

2.1 Experimental device

The experimental procedure has been described in more detail in other literature [8]. This article provides a brief description on the parameters that are closely related to this process.

The coal rock samples were collected at the Linyi mine area, Shandong Province, China. Coal rock is brittle, and dynamic disasters such as rock burst easily occur during the process of excavation. The samples were processed into dimensions of 50 mm×25 mm×100 mm. At the centre of the samples there is a 20 mm diameter hole with a radial crack with a width of 2 mm and a length of 35 mm. Different samples present different angle of the crack relatively to the central hole. The flatness error on both end surfaces was less than 0.02 mm. To rigorously screen specimens, the following is performed: 1) Removal of specimens with visible surface damage and visible cracks; 2) Removal of specimens whose size and flatness do not meet the standard requirement. The experimental results in this paper are obtained from samples with 60° inclination.

The schematic diagram regarding the experimental procedure is shown in Figure 1. The loading system, used in the experiment, was a YAW type 600 kN electro-hydraulic servo press. The system has force closed-loop control, constant stress control and load holding function, which can perform equal-load loading. In the paper, the coal rock samples are continuously loaded under uniaxial compression at a loading speed of 0.1 mm/min.

Figure 1 Schematic diagram of experimental system:

The AE waveform signal of the entire process is collected by a PCI-2 type 24-channel AE device produced by American Acoustic Physics Company. It is capable of collecting information about the AE count, energy, amplitude as well as other information during the coal rock loading and rupture process, while simultaneously acquiring the waveform of the AE signal. The dynamic signal amplitude is 100 dB; the preamplifier is 40 dB; the threshold is 40 dB; the signal peak definition time (PDT) is 200 μs; the impact definition time (HDT) is 800 μs; and the impact lockout time (HLT) is 1000 μs. The monitoring scale of AE in the laboratory is small, generally several tens of centimeters, and the frequency is relatively high, mainly concentrated in the frequency range of 20 kHz-10 MHz. For this reason, the AE sensor chosen for this experiment is the Nono 30, and the resonance frequency of this type of sensor is 300 kHz, with a sampling frequency of 2 MHz.

2.2 Experimental results

Several experiments were conducted to evaluate the susceptibility of coal samples to deformation and failure. Figure 2 shows the typical AE Energy and stress-strain curve of the coal rock. According to previous experience and analysis, the AE stress time curve is divided into the following stages: OA—Initial compaction, AB—Compacting phase, BC—Fracture initiation, CD—Plastic deformation, DE—Peak stress, EF—Post-peak failure. The original AE waveforms at different stress levels are shown in Figure 3.

Figure 2 AE energy changes with stress and time

Due to geological and mining effects, the sample presents a few pore fractures prior to the initial compaction stage (OA in Figure 2). During the initial compaction stage, the larger primary pores inside the coal rock body are compacted and closed, which are larger than the primary crack created at the end of compaction (AB in Figure 4). This process releases a relatively small AE signal. However, the AE waveform carries a relatively large amount of energy compared with the end of the compaction stage. This occurs because at the end of the compaction stage, the primary fracture of the fractured coal rock is almost completely closed. For that reason, the stress on the specimen has not reached the cracking stress for a new fracture, and so, no new crack is generated, and the AE energy is reduced to a minimum (point B in Figure (2)). The fracture slip between some small particles inside the coal rock also produces an AE waveform signal, but the compressive deformation of the coal rock is reduced compared to the initial compaction, and so is the corresponding released energy. After the end of the compacting phase, the loading ensues, and the cracking starts. Because the coal rock texture is hard and presents good compacity, no AE signal appears before the cracking starts (before point C in Figure 2). When the stress concentration of the pre-cracked tip reaches the cracking stress, the sample cracks creating a new fracture. Compared with the compaction stage, the scale of the fracture at the moment of fracture initiation is relatively large, releasing a large amount of energy. In addition, the energy carried by the AE waveform is also large (Figure 3(c)). During the plastic deformation stage, strain hardening, and strain softening occur in the fractured coal rock body, but the volume of the fractured coal rock is usually reduced before reaching the expansion point where strain softening occurs (CD in Figure 2). Hence, the process takes place is essentially strain hardening, during which the solid body suffers almost no fracture. As a result, the crack propagation is small, and the resulting released AE energy is small (near point D in Figure 2). Additionally, the waveform composition is relatively complex (Figure 3(d)). The cracks in the coal rock at the peak stress stage have been developed, but due to the existence of the solid body, the sample has not completely destabilized and collapsed. At the peak stress, the energy released by each solid body fracture is larger (near point E in Figure 2). As a result, the amplitude of the AE waveform is as large as 0.058 mV (Figure 3(e)). At post-peak failure, which is reached after the peak stress, the stable fracture of the coal rock is controlled, and the sample undergoes large-scale rupture, releasing a large amount of energy (EF in Figure 2), with the amplitude of the AE waveform increasing to a maximum of 0.2 mV (Figure 3(f)).

3 HHT theory

Hilbert-Huang transform is an adaptive time-frequency analysis method. The main steps of row data analysis are as follows [39, 43]: EMD method is used to decompose the signal, the natural mode function component of the original signal is taken, and the natural modes obtained by decomposition are analyzed, then Hilbert spectra of the IMFs are obtained by Hilbert transform.

Figure 3 Characteristics of AE waveforms:

3.1 EMD basic principles

EMD method can decompose non-stationary and non-linear signals into a set of steady-state and linear data series, namely IMF. Taking the time series data s(t) as an example, the EMD algorithm can obtain the following results:

                       (1)

where c_k(t) is the IMF; r_n(t) is the mean trend component.

3.2 Instantaneous frequency and HHT spectrum

Based on the local characteristic time scale of the signal, HHT adaptively decomposes the signal into the sum of several IMF components, and calculates the instantaneous frequency and instantaneous amplitude of each IMF component.

Hilbert transformation of each intrinsic mode function c_k(t) in Eq. (1) is obtained:

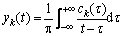                      (2)

By constructing the analytic signal, the amplitude function, phase function θ_k(t) and instantaneous frequency are obtained.

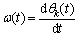　　　　　　　　　　　　　　(3)

where .

Ignoring the residual term r_n, we can have express as:

              (4)

where frequency ω_k(t) and amplitude a_k(t) are the time variables, which can form three-dimensional spectrum of time, frequency and amplitude. The signal amplitude distribution in the time-frequency plane is called Hilbert time-frequency spectrum, which is represented by H(ω, t). This can accurately describe the variation of signal amplitude with time and frequency in the whole frequency range.

The marginal spectrum h(ω) is defined as:

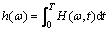                        (5)

where T is the time sequence length.

By integrating the three-dimensional time spectrum with time, a two-dimensional spectrum with only frequency and amplitude is formed. Marginal spectrum can be used to represent the cumulative amplitude distribution of each frequency point in the whole data set, and reflect the change of signal amplitude in the whole frequency range.

4 HHT characteristics of AE waveforms

In this section, HHT is used to analyze the AE waveform characteristics of coal rock at different loading stages. The original data are from Figure 3.

4.1 IMF components characteristics of AE waveforms

According to the principle of the HHT analysis method, first of all, the AE waveforms corresponding to different stages of cracking are empirically decomposed. This allows the signal to be decomposed from high frequency to low frequency by the three-spline interpolation method, thus obtaining diverse IMF components which vary in terms of frequency and energy contents. The IMF component characteristics of AE waveforms at different loading stages are shown in Figure 4.

As can be seen from Figure 4, according to the method of the three spline differences, no prior base is required, the target waveform can be automatically decomposed into 9-10 IMF components using the HHT method until interpolation in the last waveform cannot be continued. In general, the c₁ component presents the highest frequency content and a relatively large amount of energy, but not necessarily the largest magnitude, and regardless of the initial amplitude of the waveform, the energy is concentrated in the first four components. Regarding the initial loading phase of the coal rock, the waveform amplitude as well as the amplitude of each one of the components is small (Figures 4(a)-(c)). However, after the plastic deformation stage, both the magnitude of the coal rock rupture and the energy released are larger (Figures 4(d) and (e)). This is reflected by each of the AE waveform IMF components amplitude, which presents a gradually increasing trend up to the instant of instability at which point the amplitudes of the IMF components reach their maximum value. This is verified even for the last component (c₉), whose amplitude reaches a high value of 0.011 mV (Figure 4(f)). Regarding frequency, the procedure essentially comprises a gradual decomposition from high to low frequencies. The frequency decrement in the larger energy ratio c₁-c₄ IMF components is more noticeable, while the frequency change of the subsequent components (c₅-c₉) is less clear. After the plastic deformation stage, the proportion of energy in the lower frequency IMF components presents an increasing trend.

4.2 Hilbert marginal spectral characteristics of AE waveforms

The magnitude of the Hilbert margin is not the size of the amplitude in the physical sense.

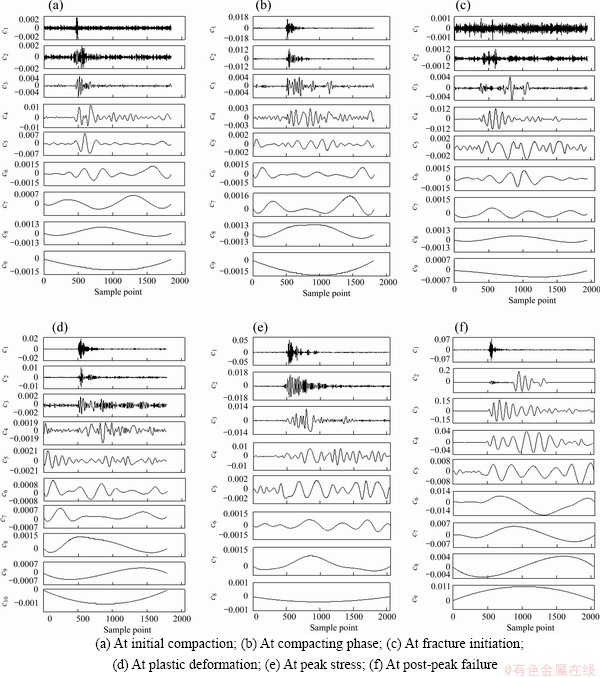
Figure 4 AE waveforms IMF components:

According to the definition of the Hilbert margin, its magnitude actually represents the scale at which the waveform has different frequency characteristics, and the greater the magnitude, the greater the likelihood of change occurring at that frequency. The Hilbert marginal spectrum of coal rock AE waveforms at different loading stages is shown in Figure 5.

As can be seen from the Hilbert marginal spectrum shown in Figure 5, the energy released by coal rock is small during the initial compression phase, and the AE waveform energy is concentrated in the low-frequency range of 0-40 kHz (Figure 5(a)). This is essentially because of the lower amount of energy released by the coal rock in the initial loading phase. At the end of the compaction stage, the frequency range with higher energy concentration has expanded (0-400 kHz). When cracking commences, the energy concentration is distributed around 20 kHz, and the energy ratio below 20 kHz is positive. In the plastic deformation phase, with the further propagation of cracks, both large and small cracks increase in size, and the energy released also increases. This results in the frequency band getting wider. The waveform energy is concentrated in the first 350 kHz, in which the 0-25 kHz and 200-350 kHz ranges have the highest energy concentration (Figure 5(d)), while the energy concentration around 150 kHz is reduced. The Hilbert marginal spectrum at stress peaks is more dispersed within the 0-200 kHz frequency band and can be clearly divided into two main bands:0-25 kHz and 60-180 kHz (Figure 5(e)). When the cracked coal rock specimen is destroyed by instability, the waveform energy is concentrated in the 0-25 kHz frequency range and reaches its maximal value at 20 kHz (Figure 5(f)).

Figure 5 AE waveforms Hilbert marginal amplitude spectra:

From the above analysis, it can be concluded that, since the marginal Hilbert spectrum is empirically decomposed, no priori base is required. Furthermore, the energy is almost 0 in the high frequency band with a very small energy ratio.

4.3 Hilbert instantaneous energy spectrum characteristics for AE waveforms

In general, the waveform energy calculated by traditional methods corresponds to either the characteristic energy of the whole process, or the energy characterization regarding frequency. However, there is less research on energy characterization regarding time, especially the real-time energy of the full waveform represented in the time domain. By definition, the Hilbert instantaneous energy provides a means to characterize the waveform energy in the time domain, thus allowing to determine the waveform energy at different instants. This provides an important reference for estimating the scale of the damage to the specimen, as well as the energy released at the rupture instants. Figure 6 shows the AE waveform Hilbert instantaneous energy during the coal rock loading process, and the value is processed as a non-quantitative scale unit, representing only the magnitude of the energy value.

Figure 6 shows that the instantaneous energy is, in general, significantly different at different stages of the waveform. There are clear instantaneous energy peaks/lows, namely the instantaneous energy is low before the waveform’s jump, and the waveform’s instantaneous energy increases rapidly peaking in 100 sample points. Since there is a large release of energy due to the coal rock’s rupture, not only the respective waveform carries different total energy, but also the instantaneous energy peak is different. Even though the energy released is low at initial compaction, the waveform’s instantaneous energy can reach a high value (Figure 6(a)), because the instantaneous energy is mainly determined by the frequency and amplitude of the waveform, where the higher the frequency, the smaller the instantaneous energy amplitude. The waveform information is related to the energy released by the coal rock rupture, which is given mainly in the form of momentary energy and waveform duration. Although the instantaneous energy peak of the waveform is high at initial compaction, the energy carried is generally small due to its short duration (only 200 sample points duration). It is also mainly because the coal rock rupture is small at initial compaction. At the end of the compression phase, along with the loading, there is a sudden energy increase, however its attenuation is relatively rapid (Figure 6(b)), and so its total energy is small. When the crack propagates, the AE energy released by the specimen is larger, which is also reflected in the waveform instantaneous energy. The instantaneous energy rises slowly from 0.15 at the sample point 400 to 1.3 at the sample point 600. Although having some variation between both points, the mean energy value is relatively high, which results in a large amount of energy in that interval (Figure 6(c). Regarding the plastic deformation stage, even though the AE waveform shows a large peak, because of its rapid attenuation, the peak value duration is short, resulting in little cumulative energy (Figure 6(d)). Moreover, Hilbert instantaneous energy is also like this at the peak stress (Figure 6(e)), the main reason is that the deformation of coal rock is not severe, and the energy release is lower at the moment. When the coal rock is instable, the rupture is large and the coal rock releases much more energy. The instantaneous energy rapidly increases from 0.2 at the sample point 500 to 1.3 at the sample point 550, and subsequently reaches 1.8 at the sample point 800, after which it slowly drops to 0.3 at the sample point 1600, and then it remains at a relatively stable low value (Figure 6(f)). The longer the coal rock rupture lasts, the higher the waveform instantaneous and total energy are.

Figure 6 AE waveforms Hilbert instantaneous energy:

The energy pattern changes in the waveforms, and that change can be perceived from the Hilbert instantaneous energy. This means that the coal rock stress level and damage degree can be estimated from the characteristics of the waveform instantaneous energy.

4.4 Hilbert three-dimensional energy spectrum characteristics of AE waveforms

The energy variation of the AE waveform, regards both time and frequency, which could be clearly conveyed by the Hilbert three-dimensional energy spectrum (Figure 7). The color bar on the right-hand side represents the energy magnitude, where a deeper color corresponds to more energy.

As can be seen from Figure 7, the Hilbert three-dimensional energy spectrum clearly shows the varying AE waveform energy patterns in the frequency and time domains, where the three-dimensional distribution of energy is intermittent rather than continuous. During the initial compression phase, in the time domain and after the low frequency and starting point, the energy is concentrated and is relatively low (Figure 7 (a)). At the end of the compression, the energy is concentrated in two bands, near 300 and 100 kHz (Figure 7(b)). The energy at the time of cracking is mainly concentrated in the low frequency band and located between the sample points 450 and 900 (Figure 7(c)), which correspond to the sample points with a larger mid-range value in the waveform. At this stage, the coal rock deformation and destruction releases relatively little energy and it is generally stable. In the plastic deformation phase, the energy is relatively dispersed, mainly concentrated around the relatively high frequency value of 300 kHz (Figure 7(d)), while the low frequency shows less energy. The energy at the peak intensity point is concentrated at around 150 kHz (Figure 7(e)), and it has the trend to the lower frequencies, which could be considered the premonitory sign of the coal rock instability. When the coal rock ruptures, the energy is concentrated at two sample point intervals, 600-800 and 1000-1300. In both cases, the frequency is essentially fixed in the low frequency band, around 25 kHz (Figure 7(f)).

From the above analysis, it could also be concluded that an advantage of the Hilbert three-dimensional energy spectrum is that the real energy spectrum is 0, and the energy spectrum is intermittent rather than continuous, unlike other methods, due to windowing and subsequent energy smoothing, suffering from loss of information quality and energy leakage.

Figure 7 AE waveforms three-dimensional Hilbert spectra:

5 Conclusions

1) AE energy at initial compaction is more than that at the end of compaction, as the coal rock larger primary pores were compressed and closed. After that, during the plastic deformation stage, the number of small-energy AE events decreases, and the number of big-energy AE events starts to increase. AE energy increases to the maximum at the post-peak failure stage, and then AE energy reduces. AE energy and AE waveform amplitude are positively correlated with fracture, but not with stress.

2) The HHT method decomposes the waveforms into different IMF components from higher frequencies to lower frequencies. However, the energy from different loading stages is mainly concentrated in the first 4 IMF components (c₁-c₄). Additionally, the frequency variation between the main components is very clear. The energy in the low-frequency IMF components, presents an increasing trend from the plastic deformation stage to peak stress and post-peak failure stage.

3) The Hilbert marginal spectrum is obtained by empirical modal decomposition. While the stress is small, and the Hilbert marginal spectrum distribution frequency is wide, which means that the waveforms could occur in a relatively wide range. With the increase of stress, the frequency of the maximum marginal energy spectrum decreases, and is concentrated in the low-frequency range when the critical instability of coal rock is reached and the sample is destroyed.

4) Hilbert instantaneous energy reflects the amount of energy of the AE waveform at different moments. Waveform frequency and amplitude are the most influential factors to the Hilbert instantaneous energy. They are indicators of the amount of energy released by coal rock and subsequently carried by the waveform. The momentary energy and waveform duration are factors influencing the Hilbert instantaneous cumulative energy. The Hilbert instantaneous cumulative energy increases with the stress and scale of the coal rock rupture, reaching its maximum value at the coal rock rupture at post-peak failure.

5) Three-dimensional Hilbert energy spectrum clearly shows the change of AE waveform energy in the frequency and time domain. In addition, it is intermittent rather than continuous. The energy is relatively dispersed in the plastic deformation stage, and it is small in the lower frequency band. From the plastic deformation stage to the instability stage, the waveform energy is mainly concentrated in the low frequency range, and it is the most obvious when the coal rock ruptures at post-peak failure.

Contributors

LI Xue-long wrote the draft of the whole manuscript. CHEN Shao-jie provided the concept and designed the experiment. LI Xue-long, LIU Shu-min and LI Zhong-hui conducted the experiment.

Conflict of interest

LI Xue-long, CHEN Shao-jie, LIU Shu-min and LI Zhong-hui declare that they have no conflict of interest.

References

[1] MARTYN D R, MARK R A, PHILIP G M. Micro cracking during triaxial deformation of porous rocks monitored by changes in rock physical properties (II)-Pore volumometry and acoustic emission measurements on water-saturated rocks [J]. Tectonophysics, 1995, 245(3, 4): 223-235. DOI: 10.1016/ 0148-9062(96)86984-1.

[2] LI Peng, REN Fen-hua, CAI Mei-feng. Investigating the mechanical and acoustic emission characteristics of brittle failure around a circular opening under uniaxial loading [J]. International Journal of Minerals, Metallurgy, and Materials, 2019, 26(10): 1217-1230. DOI: 10.1007/s12613-019-1887-5.

[3] NIU Yue, ZHANG Xin, WANG En-yuan. A new method of monitoring the stability of boreholes for methane drainage from coal seams [J]. Measurement, 2020, 154: 107521. DOI: 10.1016/j.measurement.2020.107521.

[4] LI Xue-long, CHEN Shao-jie, WANG Sheng. Study on in situ stress distribution law of the deep mine taking Linyi Mining area as an example [J]. Advances in Materials Science and Engineering, 2021: 5594181. DOI: 10.1155/2021/5594181.

[5] CHEN Shao-jie, DU Zhao-wen, ZHANG Zhen. Effects of chloride on the early mechanical properties and microstructure of gangue-cemented paste backfill [J]. Construction and Building Materials, 2020, 235(2): 117504. DOI: 10.1016/j.conbuildmat.2019.117504.

[6] MANTERLOA J, AGUIRRE M, ZURBITU J. Using acoustic emissions (AE) to monitor mode I crack growth in bonded joints [J]. Engineering Fracture Mechanics, 2020, 2241(2): 106778. DOI: 10.1016/j.engfracmech.2019.106778.

[7] LIU Xiang-xin, LIANG Zheng-zhao, ZHANG Yan-bo. Experimental study on the monitoring of rockburst in tunnels under dry and saturated conditions using AE and infrared monitoring [J]. Tunnelling and Underground Space Technology, 2018, 82(12): 517-528. DOI: 10.1016/j.tust. 2018.08.011.

[8] LOU Quan, SONG Da-zhao, HE Xue-qiu. Correlations between acoustic and electromagnetic emissions and stress drop induced by burst-prone coal rock fracture [J]. Safety Science, 2019, 115(6): 310-319. DOI: 10.1016/j.ssci.2019. 02.022.

[9] KONG Biao LIU Zhen, YAO Qing-guo. Study on the electromagnetic spectrum characteristics of underground coal fire hazardous and the detection criteria of high temperature anomaly area [J]. Environmental Earth Sciences. 2021, 80(3): 1-11. DOI: 10.1007/S12665-021-09380-5.

[10] TAN Jing-qiang, HU Cheng-er, HU Qiao. Multi-fractal analysis for the AE energy dissipation of CO₂ and CO₂+ brine/water treated low-clay shales under uniaxial compressive tests [J]. Fuel, 2019, 24615(6): 330-339. DOI: 10.1016/j.fuel.2019.03.008.

[11] WANG Kai, DU Feng. Coal-gas compound dynamic disasters in China: A review [J]. Process Safety and Environmental Protection, 2020, 133(1): 1-17. DOI: 10.1016/j.psep.2019.10. 006.

[12] WANG Shao-feng, LI Xi-bing, YAO Jin-rui. Experimental investigation of rock breakage by a conical pick and its application to non-explosive mechanized mining in deep hard rock [J]. International Journal of Rock Mechanics and Mining Sciences. 2019, 122(11): 104063. DOI: 10.1016/j.ijrmms. 2019.104063.

[13] LI Qing-miao, LIANG Yun-pei, ZOU Quan-le. Acoustic emission and energy dissipation characteristics of gas-bearing coal samples under different cyclic loading paths [J]. Natural Resources Research, 2019, 29(3): 1397-1412. 10.1007/s11053-019-09508-2.

[14] LI Xue-long, CAO Zuo-yong, XU You-lin. Characteristics and trends of coal mine safety development [J]. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 2020. DOI: 10.1080/15567036.2020.1852339.

[15] KONG Xiang-guo, WANG En-yuan, LI Shu-gang. Dynamic mechanical characteristics and fracture mechanism of gas-bearing coal based on SHPB experiments [J]. Theoretical and Applied Fracture Mechanics, 2020, 105(2): 102395. DOI: 10.1016/j.tafmec.2019.102395.

[16] CAI Wu, DOU Lin-ming, SI Guang-yao. A new seismic-based strain energy methodology for coal burst forecasting in underground coal mines [J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 123(11): 104086. DOI: 10.1016/j.ijrmms.2019.104086.

[17] YAN Fa-zhi, XU Jiang, PENG Shou-jian. Effect of capacitance on physicochemical evolution characteristics of bituminous coal treated by high-voltage electric pulses [J]. Powder Technology, 2020, 367(3): 47-55. DOI: 10.1016/j.powtec.2020.03.041.

[18] FAN Chao-jun, ELSWORTH D, LI Sheng. Thermo-hydro-mechanical-chemical couplings controlling CH₄ production and CO₂ sequestration in enhanced coalbed methane recovery [J]. Energy, 2019, 173(4): 1054-1077. DOI: 10.1016/j.energy. 2019.02.126.

[19] ZHANG Zhi-bo. WANG En-yuan, ZHANG Ying-hua. Analysis on the time-frequency characteristics of ultrasonic waveform of coal under uniaxial loading [J]. Fractals, 2019, 27(6): 1950100. DOI: 10.1142/S0218348X19501007.

[20] KONG Biao, WANG En-yuan, LU Wei. Application of electromagnetic radiation detection in high-temperature anomalous areas experiencing coalfield fires [J]. Energy, 2019, 183(12): 116144. DOI: 10.1016/j.energy.2019.116144.

[21] LIU Xian-feng, SONG Da-zhao, HE XUE-qiu. Quantitative analysis of coal nanopore characteristics using atomic force microscopy [J]. Powder Technology, 2019, 346(3): 332-340. DOI: 10.1016/j.powtec.2019.02.027.

[22] XUE Yan-chao, SUN Wen-bin, WU Quan-sen. The influence of magmatic rock thickness on fracture and instability law of mining surrounding rock [J]. Geomechanics and Engineering, 2020, 20(6): 547-556. DOI: 10.12989/gae.2020.20.6.000.

[23] LI Xue-long, LI Zhong-hui, WANG En-yuan. Microseismic signal spectra, energy characteristics and fractal features prior to rock burst: A case study in Qianqiu coal mine, China [J]. Journal of Earthquake Engineering, 2017, 21(5, 6): 891-911. DOI: 10.1080/13632469.2016.1210056.

[24] HE Man-chao, MIAO Jin-li, FENG J L. Rock burst process of limestone and its acoustic emission characteristics under true-triaxial unloading conditions [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(2): 286-298. DOI: 10.1016/j.ijrmms.2009.09.003.

[25] QIU Li-ming, SONG Da-zhao, LI Zhong-hui. Research on AE and EMR response law of the driving face passing through the fault [J]. Safety Science, 2019, 117(8): 184-193. DOI: 10.1016/j.ssci.2019.04.021.

[26] FENG Fan, CHEN Shao-jie, WANG Ya-jun. Cracking mechanism and strength criteria evaluation of granite affected by intermediate principal stresses subjected to unloading stress state [J]. International Journal of Rock Mechanics and Mining Sciences, 2021: 104783.

[27] ZHENG Chun-shan, JIANG Bing-you, XUE Sheng. Coalbed methane emissions and drainage methods in underground mining for mining safety and environmental benefits: A review [J]. Process Safety and Environmental Protection, 2019, 127(7): 103-124. DOI: 10.1016/j.psep.2019.05.010.

[28] NI Qing-qing, IWAMOTO M. Wavelet transform of acoustic emission signals in failure of model composites [J]. Engineering Fracture Mechanics, 2002, 69(6): 717-728. DOI: 10.1016/S0013-7944(01)00105-9.

[29] LIU Ting, LIN Bai-quan. Time-dependent dynamic diffusion processes in coal: Model development and analysis [J]. International Journal of Heat and Mass Transfer, 2019, 134(5): 1-9. DOI: 10.1016/j.ijheatmasstransfer.2019.01.005.

[30] FAN Jin-yang, LIU Wei, JIANG De-yi. Time interval effect in triaxial discontinuous cyclic compression tests and simulations for the residual stress in rock salt [J]. Rock Mechanics and Rock Engineering, 2020, 53(9): 4061-4076. DOI: 10.1007/s00603-020-02150-y.

[31] LI Xue-long, CHEN Shao-jie, LI Zhong-hui. Rockburst mechanism in coal rock with structural surface and the microseismic (MS) and electromagnetic radiation (EMR) response [J]. Engineering Failure Analysis, 2021, 124(6): 105396. DOI: 10.1016/j.engfailanal.2021.105396.

[32] ZHANG Chao-lin, WANG En-yuan, XU Jiang, A new method for coal and gas outburst prediction and prevention based on the fragmentation of ejected coal [J]. Fuel, 2021, 287(3): 119493. DOI: 10.1016/j.fuel.2020.119493.

[33] JEONG H, JANG Y S. Wavelet analysis of plate wave propagation in composite laminates [J]. Composite Structures, 2000, 49(4): 443-450. DOI: 10.1016/S0263-8223(00)00079-9.

[34] DING Y, REUBEN R L, STEEL J A. A new method for waveform analysis for estimating AE wave arrival times using wavelet decomposition [J]. NDT and E International, 2004, 37(4): 279-290. DOI: 10.1016/j.ndteint.2003.10.006.

[35] KONG Xiang-guo, WANG En-yuan, LI Shu-gang. Fractals and chaos characteristics of acoustic emission energy about gas-bearing coal during loaded failure [J]. Fractals, 2019, 27(5): 1950072. DOI: 10.1142/S0218348X19500725.

[36] PAN Jie-nan, LU Min-min, HOU Quan-lin. Coal microcrystalline structural changes related to methane adsorption/desorption [J]. Fuel, 2019, 239(1): 13-23. DOI: 10.1016/j.fuel.2018.10.155.

[37] CAI M, MORIOKA H, KAISER P K. Back-analysis of rock mass strength parameters using AE monitoring data [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(4): 538-549. DOI: 10.1016/j.ijrmms.2006.09.012.

[38] CHEON D S, JUNG Y B, PARK E S. Evaluation of damage level for rock slopes using acoustic emission technique with waveguides [J]. Engineering Geology, 2011, 121(1): 75-88. DOI: 10.1016/j.enggeo.2011.04.015.

[39] HUANG, N E, ZHENG S, LONG S R. A new view of nonlinear water waves: The Hilbert spectrum [J]. Annu Rev Fluid Mech, 1999, 31(1): 417-457.

[40] YANG Yu, YU De-jie, CHENG Jun-sheng. A fault diagnosis approach for roller bearing based on IMF envelope spectrum and SVM [J]. Measurement, 2007, 40(9, 10): 943-950. DOI: 10.1016/j.measurement.2006.10.010.

[41] ZOU Quan-le, LIU Han, CHENG Zhi-heng. Effect of slot inclination angle and borehole-slot ratio on mechanical property of pre-cracked coal: Implications for ECBM recovery using hydraulic slotting [J]. Natural Resources Research, 2020, 29: 1705-1729. DOI: 10.1007/s11053-019-09544-y.

[42] LI Li-ping, SHANG Cheng-shun, CHU Kai-wei. Large-scale geo-mechanical model tests for stability assessment of super-large cross-section tunnel [J]. Tunnelling and Underground Space Technology, 2021, 109(3), 103756. DOI: 10.1016/J.TUST.2020.103756.

[43] LOH C H, WU T C, HUANG N E. Application of the empirical mode decomposition Hilbert spectrum method to identify near-fault ground-motion characteristics and structural responses [J]. Bulletin of the Seismological Society of Americal, 2001, 91: 1339-1357. DOI: 10.1785/01200 00715.

[44] LIU Jie, ZHANG Ran, SONG Da-zhao. Experimental investigation on occurrence of gassy coal extrusion in coalmine [J]. Safety Science, 2019, 113(3): 362-371. DOI: 10.1016/j.ssci.2018.12.012.

[45] LI Xue-long, LI Zhong-hui, WANG En-yuan. Extraction of microseismic waveforms characteristics prior to rock burst using Hilbert-Huang transform [J]. Measurement, 2016, 91(9): 101-113. DOI: 10.1016/j.measurement.2016.05.045.

[46] QIN Lei, LI Shu-gang, ZHAI Cheng. Changes in the pore structure of lignite after repeated cycles of liquid nitrogen freezing as determined by nitrogen adsorption and mercury intrusion [J]. Fuel, 2020, 267: 117214. DOI: 10.1016/j.fuel. 2020.117214.

[47] LI Xi-bing, ZHANG Yi-ping, LIU Zhi-xiang. Wavelet analysis and Hilbert-Huang transform of blasting vibration signal [J]. Explosion and Shock Waves, 2005, 25(6): 528-535. DOI: 10.11883/1001-1455(2005)06-0528-08.

[48] SHEN Wen-long, SHI Guo-cang, WANG Meng. Method of entry layout under synergistic effects of abutment stress and dynamic stress [J]. Shock and Vibration, 2020: 1-16. DOI: 10.1155/2020/6655293.

[49] LIU Shu-min, LI Xue-long, WANG Deng-ke. Experimental study on temperature response of different ranks of coal to liquid nitrogen soaking [J]. Natural Resources Research, 2021, 32(2): 1467-1480. DOI: 10.1007/s11053-020-09768-3.

[50] NGAMSIRIJIT P, WATCHARAWITTAYAKUL T, JARUMANEEROJ P. Antral contraction rate estimation from dynamic antral scintigraphy using Hilbert-Huang transform [J]. Computers in Biology and Medicine, 2020, 117(2): 103560. DOI: 10.1016/j.compbiomed.2019.103560.

[51] SUSANTO A, LIU C H, YAMADA K, Application of Hilbert–Huang transform for vibration signal analysis in end-milling [J]. Precision Engineering, 2018, 53(7): 263-277. DOI: 10.1016/j.precisioneng.2018.04.008.

[52] BANDARA S, RAJEEV P, GAD E. Damage detection of in service timber poles using Hilbert-Huang transform [J]. NDT & E International, 2019, 107(10): 102141. DOI: 10.1016/j.ndteint.2019.102141.

[53] VELTCHEVA A, SOARES C G. Analysis of wave groups by wave envelope-phase and the Hilbert-Huang transform methods [J]. Applied Ocean Research, 2016, 60(10): 176-184. DOI: 10.1016/j.apor.2016.09.006.

[54] HU Jian-ping, WANG Xiao-chao, QIN Hong. Novel and efficient computation of Hilbert-Huang transform on surfaces [J]. Computer Aided Geometric Design, 2016, 43(3): 95-108. DOI: 10.1016/j.cagd.2016.02.011.

(Edited by ZHENG Yu-tong)

中文导读

基于HHT分析的岩体单轴加载声发射波形特征

摘要：声发射波形包含煤岩体失稳破坏的微观细致结构特征，为了得到煤岩体在不同加载阶段更多的煤岩失稳细观结构特征，本文采用HHT方法对不同加载阶段的声发射波形特征进行分析。研究结果表明，HHT可以将目标波形分解成多个IMF分量，能量主要集中在c₁~c₄ IMF分量，其中c₁分量频率最高，能量也最大，随着加载进行低频IMF分量所占的能量比例呈现增加的趋势。Hilbert边际谱在初始压密阶段集中在0~40 kHz的低频部分，塑性变形阶段在0~25 kHz和200~350 kHz的范围内有明显的能量集聚特征，而在失稳破坏时集中在0~25 kHz，并在20 kHz时达到最大。各个阶段均有一个较为明显的瞬时能量峰值，在初始压密和压密结束阶段波形的瞬时能量峰值较高，但由于波形有效持续时间较短，携带的总体能量较小，破坏时瞬时能量高值持续时间较长，波形的总能量达到最大。Hilbert三维能量谱在真实能量为0的区域，其能量谱一般为0，并且分布是断续而非连续的，跟前述几个动态范围的特点是一致的，但更为明显地表明了失稳破坏临界阶段的能量低频集聚。该研究反映了煤岩失稳破坏演化过程的地球物理信号的响应规律，为监测煤岩动力灾害提供依据。

关键词：声发射；波形；Hilbert-Huang变换；岩石

Foundation item: Projects(51904167, 51474134, 51774194) supported by the National Natural Science Foundation of China; Project(SKLCRSM19KF008) supported by the Research Fund of the State Key Laboratory of Coal Resources and Safe Mining, CUMT, China; Project(cstc2019jcyj-bsh0041) supported by the Natural Science Foundation of Chongqing, China; Project(2011DA105287-BH201903) supported by the Postdoctoral Science Foundation Project Funded by State Key Laboratory of Coal Mine Disaster Dynamics and Control, China; Project(2019SDZY034-2) supported by the Key R&D plan of Shandong Province, China; Project(2020M670781) supported by the China Postdoctoral Science Foundation; Project supported by the Taishan Scholars Project; Project supported by the Taishan Scholar Talent Team Support Plan for Advantaged & Unique Discipline Areas, China

Received date: 2020-12-10; Accepted date: 2021-04-11

Corresponding author: CHEN Shao-jie, PhD, Professor; Tel: +86-532-86057948; E-mail: chensj@sdust.edu.cn; ORCID: https://orcid. org/0000-0003-1377-0808

Abstract: Acoustic Emission (AE) waveforms contain information on microscopic structural features that can be related with damage of coal rock masses. In this paper, the Hilbert-Huang transform (HHT) method is used to obtain detailed structural characteristics of coal rock masses associated with damage, at different loading stages, from the analyses of the characteristics of AE waveforms. The results show that the HHT method can be used to decompose the target waveform into multiple intrinsic mode function (IMF) components, with the energy mainly concentrated in the c₁-c₄ IMF components, where the c₁ component has the highest frequency and the largest amount of energy. As the loading continues, the proportion of energy occupied by the low-frequency IMF component shows an increasing trend. In the initial compaction stage, the Hilbert marginal spectrum is mainly concentrated in the low frequency range of 0-40 kHz. The plastic deformation stage is associated to energy accumulation in the frequency range of 0-25 kHz and 200-350 kHz, while the instability damage stage is mainly concentrated in the frequency range of 0-25 kHz. At 20 kHz, the instability damage reaches its maximum value. There is a relatively clear instantaneous energy peak at each stage, albeit being more distinct at the beginning and at the end of the compaction phase. Since the effective duration of the waveform is short, its resulting energy is small, and so there is a relatively high value from the instantaneous energy peak. The waveform lasts a relatively long time after the peak that coincides with failure, which is the period where the waveform reaches its maximum energy level. The Hilbert three-dimensional energy spectrum is generally zero in the region where the real energy is zero. In addition, its energy spectrum is intermittent rather than continuous. It is therefore consistent with the characteristics of the several dynamic ranges mentioned above, and it indicates more clearly the low-frequency energy concentration in the critical stage of instability failure. This study well reflects the response law of geophysical signals in the process of coal rock instability and failure, providing a basis for monitoring coal rock dynamic disasters.