Constitutive description of casting aluminum alloy based on cylindrical void-cell model
CHEN Bin(陈 斌)1, PENG Xiang-he(彭向和)1, ZENG Xiang-guo(曾祥国)2,
WU Xin-yan(吴新燕)1, SUN Shi-tao(孙士涛)1
1. Department of Engineering Mechanics, Chongqing University, Chongqing 400044, China;
2. Department of Civil Engineering and Mechanics, Sichuan University, Chengdu 610065, China
Received 28 July 2006; accepted 15 September 2006
Abstract:
Casting aluminum alloys are highly heterogeneous materials with different types of voids that affect the mechanical properties of the material. Through the analysis of a cylindrical void-cell model the evolution equation of the voids was obtained. The evolution equation was embedded into a nonclassical elastoplastic constitutive relation, and an elastoplastic constitutive relation involving void evolution was obtained. A corresponding finite element procedure was developed and applied to the analyses of the distributions of the axial stress and porosity of notched cylindrical specimens of casting aluminum alloy A101. The computed results show good agreement with experimental data.
Key words:
aluminum alloy; cylindrical void; void evolution; elastoplasticity;
1 Introduction
Casting aluminum alloys are attracting increasing attention in transportation vehicle applications due to their desirable characteristics in reducing vehicle mass and amenability to recycling. For example, casting aluminum alloy A101 is currently being considered for automotive applications such as engine blocks and cylinder heads. However, because casting aluminum alloys contract when they are solidified, and hydrogen dissolves easily in the melted metals, the materials inevitably contain a certain amount of voids[1]. These voids may grow during a mechanical loading process, which may degrade the ductility of the materials and cause ductile fracture of the materials. The constitutive relation of casting aluminum alloys should include the effect of the void evolution on the mechanical properties of the materials and the analytical method for the ductile fracture of porous materials can be used in the analysis.
In order to study the effect of void evolution on the mechanical properties of porous materials, a feasible method used frequently is based on the analysis of a simple representative void-cell model of the materials. In this aspect, GURSON[2] made a pioneering contribution. He assumed that the void-matrix aggregate of a porous ductile media could be represented with a rigid-plastic cell containing a single void, and the void volume fraction (porosity) f of the cell was equal to that of the aggregate. With this method a constitutive model for a cell containing a circular-cylindrical or spherical void was obtained. REUSCH et al[3] extended Gurson’s model to the case of isotropic ductile damage and crack growth. LICHT et al[4] investigated the growth of a cylindrical void in a finite shell of a nonlinear viscous material and obtained a closed solution. SIRUGUET et al[5] modeled the effect of inclusions on void growth in porous ductile metal. LI et al[6] investigated the growth of voids embedded in elastic-plastic matrix materials with a finite element approach. MARIANI et al[7] built an orthotropic constitutive model for porous ductile media based on the micromechanical analysis of a cylindrical representative volume element. TVERGAARD et al[8] analyzed the effects of nonlocal plasticity on the interactions of voids of different sizes based on an axisymmetric unit cell model with special boundary conditions. BAASER and GROSS[9] analyzed the growth of microvoids in a ductile material in a crack tip loaded by a remote KI field. HORSTEMEYER et al[10] investigated the rate equations with internal state variables in continuum framework to model void nucleation, growth and coalescence in a casting Al-Si-Mg aluminum alloy.
The work presented here is to extend the foregoing researches in porous ductile medias to the researches of the void evolution and the elastoplastic behavior of casting aluminum alloys. A method of combining the equation of void evolution with a nonclassical elastoplastic constitutive relation was adopted in this research. The equation of void evolution was presented based on the analysis of a cylindrical void-cell model. The nonclassical elastoplastic constitutive relation is the endochronic one which does not require the notion of yield surface and can be used to describe the mechanical behavior of casting aluminum alloys. The equation of the evolution of the cylindrical void-cell model was embedded in the nonclassical constitutive relation in order to consider the void effect on the behavior of the materials. The obtained constitutive description involving void evolution and the corresponding finite element implementation was used to analyze the distributions of the axial stress and the porosity of notched cylindrical tensile specimens.
2 Cylindrical void-cell model and void evolu- tion equation
Because cylindrical voids are often found in casting aluminum alloy materials that may result from cylindrical silicon inclusions, it is supposed that the voids in the materials are of cylindrical shape. A cylindrical void-cell model is presented which is a cylindrical cell with a cylindrical void at its center (Fig.1). Suppose the matrix of the model is incompressible, the following relation can be obtained from Fig.1:
(1)
where R and r are the initial and current radii of an arbitrary point in the matrix of the model, respectively; l0 and l are the initial and current lengths of the void-cell model, respectively. Integrating Eqn.(1) gives
(2)
where a0, b0 and a, b are inner, outer initial and current radii of the void-cell model, respectively. From the definition of the volume fraction of void, the initial and current volume fractions of the cylindrical void can be expressed as
(3)
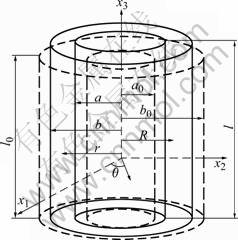
Fig.1 Schematic diagram cylindrical void-cell model
Introducing logarithmic strain, the following relations can be given:
, 
(4)
Combining Eqns.(2), (3) and (4), the following relation can be obtained:
(5)
Eqn.(5) is the evolution equation of the cylindrical void, which shows that the current void volume fraction is related to the initial void volume fraction and volumetric strain.
3 Constitutive description
Endochronic elastoplastic constitutive equation, introduced by VALANIS[11], is a kind of nonclassical constitutive equation which does not require the notion of yield surface. Because the most casting aluminum alloys do not distinctly exhibit yield, the endochronic constitutive equation was used to describe the mechanical behavior of casting aluminum alloys. The incremental form of the constitutive equation can be written as[12]
(6)
(7)
where Δsij, Δeij and 
are the increments of deviatoric stress, strain and plastic strain, respectively; Δz and zn are the increments of intrinsic time and the scale of intrinsic time after nth increments of loading; Cr, αr and G are material parameters which can be determined from σ—εp curve using a nonlinear curve fitting approach[13]. Because the void evolution will decrease the resistances to the elastoplastic deformation of a material (softening the material), a softening function w(f), which may depend on the current void volume fraction, is embedded in the constitutive equation for reflecting the softening effect of the void evolution on material properties. Because the material parameter Cr in Eqn.(6) reflects the resistances to the elastoplastic deformation of the materials and may change from Cr to (Cr)v during the void evolution, the following relation can be given:
(8)
where the softening function w(f) can take the following simple form:
(9)
From Eqns.(6) and (8) the constitutive equation involving void evolution can be written as
(10)
where
(11)
(12)
Keeping in mind Eqn.(7), Eqn.(10) can be rewritten as
(13)
where
, 
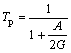(14)
It can be explicitly seen form Eqn.(10) that the void evolution markedly affects the stress response of the material. Taking tensile loading as an example, because w(f) is a monotonically decreasing function, and all other quantities in Eqn.(10) are positive, the increase in the void volume fraction f results in a reduction of the deviatoric stress 
.
4 Comparison between theoretical and experimental results
The presented constitutive model and the corresponding finite element approach were used to analyze the distributions of the axial stress and the porosity along the notch line of the notched cylindrical tensile specimens of casting aluminum alloy A101. The computed results were compared with the test data. The geometry of the notched cylindrical specimens is shown in Fig.2. The upper and right quarter of the specimens was taken for the analysis due to the symmetry of the problems. The eight-node isoparametric element with 
Gaussian points adopted. The axial displacements were prescribed at the end of the specimens with the incremental step 0.02 mm, and no radial constraint is applied to the surface of the specimens. The experimental data were obtained from tensile tests conducted on an Instron 1342 material testing system. In order to experimentally determine the distribution of the porosity in the specimens, the cylindrical specimens were loaded to 30 kN and then unloaded. After experi- ments, these specimens were cut along the minimum cross sections of the tested specimens and polished, and a photo-interpreter was used to quantify the porosity on the minimum cross sections of these specimens. Since the void distribution is stochastic, a quantitative metallographic method was adopted. Figs.3 and 4 show the distributions of the axial stress and porosity along the notch line, where a is the distance from the surface, the coordinate 0 denotes the surface, and 5 mm denotes the center of the smallest cross sections of the specimens. It can be seen from Fig.3 that the axial stress reaches its maximum value at the root of the notch and decreases rapidly toward the center of the specimen. The larger the initial porosity is, the larger the axial stress is. From Fig.4 it can be found that the porosity also reaches its maximum value near the root of the notch of the specimen, and the computed and the experimental results show reasonably agreement. Fig.5 shows a metallograph at the fracture section of the specimens obtained with a scanning electron microscope, from which many dimples can be observed. These dimples are indicative of ductile fracture of the material.
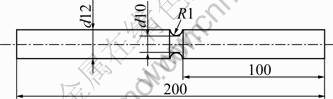
Fig.2 Schematic diagram of cylindrical tensile specimen with notch (mm)
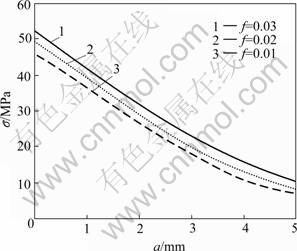
Fig.3 Distribution of axial stresses along radius of smallest section
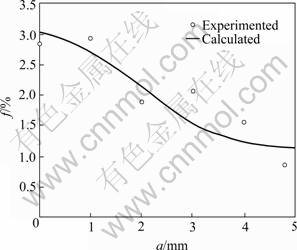
Fig.4 Distribution of porosity along radius of smallest section
Fig.5 SEM image of fractured section of specimen
5 Conclusions
1) Based on the cylindrical void-cell model and the assumption of matrix incompressibility, the equation of the void evolution for a casting aluminum alloy is derived.
2) The evolution equation is embedded in a nonclassical elastoplastic constitutive relation, and an elastoplastic constitutive relation involving void evolution is obtained.
3) A corresponding finite element procedure is developed and applied to the analyses of the distributions of the axial stress and the porosity of the notched cylindrical specimens of casting aluminum alloy A101. The computed results show good agreement with experimental data.
References
[1] BUFFIERE J Y, SAVELLI S, JOUNEAU P H, MAIRE E, FOUGERES R. Experimental study of porosity and its relation to fatigue mechanisms of model Al-Si7-Mg0.3 cast Al alloys [J]. Mater Sci Eng A, 2001, A316: 115-126.
[2] GURSON A L. Continuum theory of ductile rupture by void nucleation and growth: Part I—Yield criteria and flow rules for porous ductile media [J]. ASME J Engineering Materials and Technology, 1977, 99: 2-15.
[3] REUSCH F, SVENDSEN B, KLINGBELL D. A non-local extension of Gurson-based ductile damage modeling [J]. Composite Materials Science, 2003, 26: 219-229.
[4] LICHT C, SUQUQUET P. Growth of cylindrical void in nonlinear viscous material at arbitrary void volume fractions: a simple model [J]. Archives of Mechanics, 1988, 40: 741-757.
[5] SIRUGUET K, LEBLOND J B. Effect of void locking by inclusions upon the plastic behavior of porous ductile solids—I: Theoretical modeling and numerical study of void growth [J]. Int J Plasticity, 2004, 20: 225-254.
[6] LI G C, LING X W, SHEN H. On the mechanism of void growth and the effect of straining mode in ductile materials [J]. Int J Plasticity 2000, 16: 39-57.
[7] MARIANI S, CORIGLIANO A. Anisotropic behavior of porous, ductile media [J]. Int J Solids and Structure, 2001, 38: 2427-2451.
[8] TVERGAARD V, NIORDSON C. Nonlocal plasticity effects on interaction of different size voids [J]. Int J Plasticity, 2004, 20: 107-120.
[9] BAASER H, GROSS D. Analyses of void growth in a ductile material in front of a crack tip [J]. Computational Materials Science, 2003, 26: 28-35.
[10] HORSTEMEYER M F, LATHROP J, GOKHALE A M, DIGHE M. Modeling stress state dependent damage evolution in a cast Al-Si-Mg aluminum alloy [J]. Theoretical and Applied Fracture Mechanics, 2000, 33: 31-47.
[11] VALANIS K C. A theory of viscoplasticity without a yield surface, Part I—General theory (part II): Application to mechanical behavior of materials [J]. Archives of Mechanics, 1971, 25: 517-551.
[12] PENG X, FAN J. Numerical approach for nonclassical plasticity [J]. Computers and Structures, 1993, 47: 313-320.
[13] FAN J, HUANG J, ZENG X. Microscopically based constitutive relations for damage mechanics and creep-plasticity interaction [J]. Nuclear Engineering and Design, 1989, 116: 307-313.
(Edited by LI Xiang-qun)
Foundation item: Projects(10572157, 10272120) supported by the National Natural Science Foundation of China; Project(2006BB4143) supported by the Natural Science Foundation of Chongqing City, China
Corresponding author: CHEN Bin; Tel: +86-23-65103597; E-mail: bchen@cqu.edu.cn
