Trans. Nonferrous Met. Soc. China 27(2017) 2454-2463
Influence of process parameters on properties of AA6082 in hot forming process
Wen-yu MA1, Bao-yu WANG1, Jian-guo LIN1,2, Xue-feng TANG1
1. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. Department of Mechanical Engineering, Imperial College London, London SW7 2AZ, UK
Received 7 July 2016; accepted 21 March 2017
Abstract:
The influences of process parameters on mechanical properties of AA6082 in the hot forming and cold-die quenching (HFQ) process were analysed experimentally. Transmission electron microscopy was used to observe the precipitate distribution and to thus clarify strengthening mechanism. A new model was established to describe the strengthening of AA6082 by HFQ process in this novel forming technique. The material constants in the model were determined using a genetic algorithm tool. This strengthening model for AA6082 can precisely describe the relationship between the strengths of formed workpieces and process parameters. The predicted results agree well with the experimental ones. The Pearson correlation coefficient, average absolute relative error, and root-mean-square error between the calculated and experimental hardness values are 0.99402, 2.0054%, and 2.045, respectively. The model is further developed into an FE code ABAQUS via VUMAT to predict the mechanical property variation of a hot-stamped cup in various ageing conditions.
Key words:
aluminium alloy AA6082; mechanical properties; strengthening model; hot forming;
1 Introduction
Aluminium alloys are suitable materials for manufacturing automotive parts because of their good recyclability and light weight. In recent years, consider- able effort has been devoted to aluminium alloys in order to save resources and protect the environment [1-4]. The Al-Mg-Si series of aluminium alloys are increasingly being used because of their low density, high specific strength, and heat-treatability [5,6]. To overcome the disadvantage of low formability at room temperature, a novel hot forming technique, known as the hot forming and cold-die quenching (HFQ) process has been proposed. The HFQ process for aluminium alloys involves the solution heat treatment (SHT) of an aluminium alloy blank. Afterward, the blank is moved to cold dies for deformation. As the blank is deformed at an elevated temperature, it exhibits high formability, which is conducive to the formation of complex parts. Next, the part is subjected to artificial ageing to enhance its strength. During artificial ageing, the strengthening phase precipitates from the supersaturated solid solution (SSSS), which is formed after quenching. Generally, the precipitation sequence for Al-Mg-Si alloys is recognized as follows [7-9]: SSSS → formation of atomic clusters (Mg,Si)→GP zones→β″ precipitates→ β′ precipitates → β-Mg2Si precipitates.
Several researchers have devoted efforts to the investigation of part properties in the HFQ process because the properties of a formed part are critical to its automotive application [9]. FAN et al [7] examined the characteristics and mechanism of strengthening by the HFQ process in the 6A02 aluminium alloy. They analysed the effect of the quenching rate on the final part properties. FAN et al [8] developed a special device to experimentally investigate the HFQ process in 6A02 aluminium alloy sheets. These researchers studied the effect of solution treatment on the Vickers hardness of the formed part. The strengthening mechanism was further clarified. MA et al [9] experimentally studied the influence of SHT on the mechanical response and fracture behaviour of AA6082 sheets. Given the controversy between the role of ductility and strength in the formed parts, a multi-objective optimization tool was employed to obtain the optimal process parameters. Fracture behaviour analysis was further used to elucidate the property evolution of AA6082 in the HFQ process. YUAN et al [10] studied the effect of the die temperature on the strengthening behaviour of HFQ-formed parts of the aluminium alloy 2A12. The microstructural examination was carried out by SEM and TEM.
Several researchers have developed strengthening models for predicting the mechanical properties of various aluminium alloys. ZHANG et al [11] developed a unified constitutive model for the strengthening response of heat-treatable aluminium alloys. The precipitates in these aluminium alloys should be plate- or rod-shaped. The model includes the dislocation density and volume fraction of precipitates, both of which have an effective contribution to the strengthening response. HO et al [12] established a unified ageing-creep constitutive equation to describe the heat-treatable strengthening aluminium alloy 7010 after constant stress-creep experiments. The model considers the relationship between the precipitate radius and mechanical properties. LIU et al [13] developed a model for the strengthening response of a series of aluminium alloys, including 6061, Al-Cu binary alloys, and Al-Zn-Mg alloys. Needle/rod-shaped or plate precipitates were contained in these aluminium alloys, which can be heat-treatable. POOLE et al [14] modelled the influence of deformation on the strengthening response of the AA7018 and AA7030 alloys, using internal state variable method. ESMAEILI et al [15] developed a physical model for AA6111, in which they considered the dependence of material strength on the volume fraction and average size of precipitates. HOU et al [16] proposed a physical model following the Orowan mechanism to describe the microstructure and strength variation of an Al-Cu-Mg-Ag aluminium alloy.
However, a model to describe the strengthening of the AA6068 alloy in the HFQ process has not been reported to date. In this work, a physical and thermal simulation of the HFQ process was conducted using the Gleeble 3500 simulator. The effect of process parameters, for example, the hot-degree of deformation, strain rate and ageing time on the mechanical properties of the parts was studied. TEM was used to observe the precipitate distribution, in order to further understand the strengthening mechanism. Following this, a strengthening model corresponding to this strengthening mechanism was established. The strengthening model was programmed in FORTRAN and developed into an FE code ABAQUS via a subroutine called Variable User MATerial (VUMAT) to predict the hardness distribution of a hot-stamped cup in various ageing conditions.
2 Experimental
2.1 Materials
The material used in this work was the aluminium alloy AA6082, provided by ALCOA Company in T4 condition. The chemical composition of this alloy is illustrated in Table 1.
Table 1 Chemical composition of aluminium alloy AA6082 (mass fraction, %)

2.2 Design of experiments
Figure 1(a) shows the dimensions of the workpiece used for thermal-mechanical simulation in Gleeble 3500. The width was 50 mm, the length was 150 mm, and the thickness was 1.5 mm. The rolling direction was along the length of the workpiece. Figure 1(b) shows the dimensions of the dog-bone workpiece and the small squares, which were used for further analysis. Because the temperature uniformity of the part employed in Gleeble 3500 was estimated to be 20 mm after thermal tests [17], the dimensions of the workpieces cut from the part were designed to ensure that the small workpieces used for further analysis were within the area of temperature uniformity.

Fig. 1 Dimensions of original workpiece before experiments (a) and dog bone and small square pieces (b) (Unit: mm)
In the hot stamping experiments of AA6082, the blank was first soaked at the SHT temperature (525 °C) for a period of time. Next, the hot blank was moved to the cold die for deformation. During the transfer, the hot blank lost some heat to the air and the temperature of the blank dropped at a rate of approximately 10 °C/s. The stamping operation was initiated once the blank had been located on the die. After deformation, the part was held in the die for quenching after deformation, during which its temperature decreased at a rate of approximately 50 °C/s. The part was then subjected to artificial ageing at a temperature of 190 °C to enhance its strength [18]. The thermal-mechanical simulation tests were designed according to the real hot stamping process of AA6082. Figure 2 shows the temperature profile of the thermo- mechanical simulation. The temperature was first increased to 500 °C at a rate of 10 °C/s, and then from 500 to 525 °C at a rate of 5 °C/s to avoid overheating. The workpiece was held at this temperature for approximately 300 s. Next, the temperature was decreased from 525 to 500 °C at a rate of 10 °C/s. When the temperature reached 500 °C, the workpiece began to deform; at the same time, the temperature continued to decrease at a rate of 50 °C/s. After deformation, the temperature was dropped to room temperature at a rate of 50 °C/s. Before these experiments, thermal tests were carried out to measure the temperature distribution of the workpiece. The uniform-temperature section of the thermal simulator Gleeble 3500 was set to be 20 mm [17]. After quenching, two dog-bone parts and five small squares were cut using a wire-electrode cutting machine according to the dimensions shown in Fig. 1(b). These two dog-bone workpieces were cut within the uniform temperature section. One dog-bone workpiece was evaluated by tensile testing at room temperature, while the other was subjected to a tensile test at room temperature after artificial ageing at 190 °C for 9 h. To decrease the measurement error, the workpiece sides were smoothed using abrasive paper before the mechanical property tests at room temperature. Four of the five small squares were artificially aged at 190 °C for 0, 3, 6, and 9 h, respectively, and the remaining square was set aside as a spare. These five small squares had a width of 5 mm and were located in the centre of the workpiece, thus minimizing the effect of the inhomogeneity in temperature distribution.
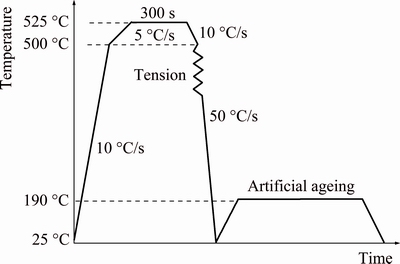
Fig. 2 Temperature profile of simulated thermal experiments
The main design factors analysed in this work include the degree of deformation (0, 10% and 30%), strain rate (0.01, 0.1 and 1 s-1), and ageing time. In each case, the small workpieces were artificially aged for 0, 3, 6 and 9 h, respectively.
Figure 3 shows the workpiece after quenching, with a degree of deformation of 10%. There were two lines near the middle of the workpiece, each with a width of 20 mm. The colour of the workpiece surface between these two lines was a little deeper than that of the other areas.

Fig. 3 Workpiece after tension deformation in Gleeble 3500, with degree of deformation of 10%
Figure 4 shows the workpiece with a degree of deformation of 30%; thus, the width of the middle part of the workpiece shows slight narrowing. The dog-bone and five small squares were cut using a wire-electrode cutting machine.

Fig. 4 Workpiece with degree of deformation of 30% after wire-electrode cutting
After the wire-electrode cutting, the grease and stains on the workpieces were cleaned using acetone, anhydrous alcohol and water. Subsequently, after artificial ageing, the small square was subjected to mounting, grinding and polishing. The workpiece was first polished using sandpaper and then ground to cloth with grinding paste until the face of the workpiece resembled a mirror. Then, the hardness was tested using a Vickers hardness tester. Every piece was tested at a minimum of five points, and the dwell time for each point was 15 s. The average value and corresponding deviation were calculated for the available points. Figure 5 shows a workpiece after hardness testing.

Fig. 5 Square workpiece after artificial ageing used for hardness measurement
3 Results and discussion
3.1 Effect of degree of deformation and ageing on ultimate tensile strength
Figure 6 shows the effect of the degree of deformation and artificial ageing on the tensile strength under a strain rate of 1 s-1. The ultimate tensile strength increases with increasing degree of deformation, and artificial ageing can markedly increase the tensile strength. Because a higher degree of deformation increases the number of dislocations, the strengthening effect is correspondingly enhanced. At the same time, during artificial ageing, the increase in the number of dislocations facilitates the nucleation of the precipitated phase. Thus, artificial ageing significantly increases the strength [14].

Fig. 6 Relationship between ultimate tensile strength and degree of deformation before and after ageing with strain rate of 1 s-1
3.2 Effect of strain rate and ageing on ultimate tensile strength
Figure 7 shows the influence of strain rate and artificial ageing on the ultimate tensile strength. With increasing strain rate, the ultimate tensile strength increases. Artificial ageing also obviously enhances the strength. With the increase of strain rate, the number of dislocations increases, and dislocation softening occurs within a limited time. After this point, the effect of dislocation recovery becomes insignificant. Higher dislocation density could increase the final strength, as explained above.
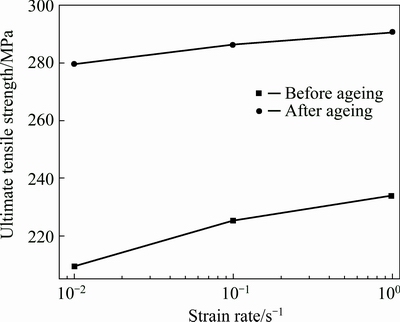
Fig. 7 Relationship between ultimate tensile strength and strain rate before and after ageing with degree of deformation of 30%
3.3 Effect of degree of deformation and ageing time on hardness
Figure 8 demonstrates the relationship between Vickers hardness and the degree of deformation and ageing time. Hardness increases with increasing degree of deformation and ageing time, which is coincident with the results in Fig. 6. The reasons are similar in these two cases. The increase is initially sharp and then becomes smooth. When the ageing time is less than 6 h, hardness increases quickly with the increase of ageing time. When the ageing time exceeds 6 h, hardness increases gradually. When the degree of deformation is 30%, hardness drops slightly as the ageing time exceeds 6 h, which is due to the over-ageing effect. The workpiece tends to be overaged when the degree of deformation is high. Deformation promotes dislocation and the nucleation of precipitates, and then within a relatively short ageing period, the aged material reaches its peak strength. Over-ageing occurs with increasing ageing treatment.

Fig. 8 Effect of degree of deformation and ageing time on Vickers hardness with strain rate of 1 s-1
3.4 Effect of strain rate and ageing time on hardness
Figure 9 shows the effect of strain rate and ageing time on hardness. Hardness increases with increasing strain rate and ageing time, similar to the trend in Fig. 7. The reasons for both cases are similar. At high ageing time, the curves show a slight decrease, which is due to the over-ageing effect. A high strain rate and large degree of deformation can enhance the effect of ageing, due to which over-ageing may occur easily [14].

Fig. 9 Effect of strain rate and ageing time on Vickers hardness with degree of deformation of 30%
Figure 10 shows a TEM image for the part obtained after hot forming at a degree of deformation of 30%, strain rate of 1 s-1 and artificial ageing for 6 h. The type of TEM used in experiment is Zeiss Libra 200, and the method for sample preparation is ion thinning. The precipitates are uniformly distributed in the matrix and are shaped as fine needles. They are designated as β″(Mg2Si) in terms of size comparison and morphology observation [7,18], both of which are assumed to have a significant effect on the strength of AA6082 [19,20].

Fig. 10 TEM image of AA6082 for workpiece obtained after hot forming at degree of deformation of 30%, strain rate of 1 s-1, and artificial ageing for 6 h
4 Development of strengthening model
4.1 Description of strengthening model
In terms of the 6xxx-series of aluminium alloys, the strength effect mainly consists of dislocation strength, solid solution strength, and precipitation strength. The overall strength is the sum of the strength branches.
4.1.1 Strength contribution of dislocation
Dislocation strength mainly originates from the degree of deformation and strain rate during hot forming. The increase in dislocation significantly affects the final strength of the part. The related literature is referenced to establish the equation for the contributions of strain and strain rate on the increment of dislocation [14]. The exponential form is used to increase the flexibility of the equation:
 (1)
(1)
where 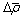 is the increment of dislocation,
is the increment of dislocation, 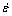 is the strain rate,
is the strain rate, 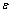 is strain, and n1, n2, n3, n4 and n5 are material constants.
is strain, and n1, n2, n3, n4 and n5 are material constants.
According to Ref. [11], the relationship between strength and dislocation in terms of these heat-treatable aluminium alloys comprising needle-shaped precipitates can be presented as follows:
 (2)
(2)
where Cdis is the equation coefficient and n6 is a material constant. In consideration of the similar strengthening mechanisms of the 6xxx-series aluminium alloys and in the interest of simplicity, the values of Cdis and n6 can be chosen as 197.2 and 0.5 based on Ref. [11].
4.1.2 Strength contribution of precipitates
The equation for normalized volume fraction of precipitates is established on the basis of Refs. [21,22] and the Avrami equation. The ageing temperature for AA6082 during the artificial ageing process is fixed at 190 °C to increase material strength [19,23]. At the ageing temperature of 190 °C, the volume fraction of precipitates increases with increasing ageing time. As ageing proceeds, more precipitates nucleate, and these precipitates grow in size by absorbing the surrounding elements. Thus, the volume fraction of precipitates varies between 0 and 1. The equation for the relationship between the volume fraction of precipitates and ageing time takes the form:
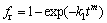 (3)
(3)
where t is the ageing time, fr is the volume fraction of precipitates, and k1 and m are material constants.
The relationship between precipitation strength and the volume fraction of precipitates can be established on the basis of the precipitation strengthening equation in Refs. [24,25]. However, in practical experiments, the overall strength decreases because of the aforementioned over-ageing effect. In order to account for the over-ageing effect, a subtractor pb is added to the volume fraction of precipitates, and the equation is modified to an exponential form with a parabolic equation. Thus, it can cover and describe the phenomena of under-ageing, peak-ageing and over-ageing. The precipitation strengthening equation is presented as
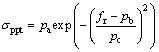 (4)
(4)
where σppt is the precipitation strength, and pa, pb and pc are material constants.
4.1.3 Strength contribution of solid solution
The solid solution contributes significantly to the strength, and this contribution is mainly related to the alloying elements dissolved in the matrix. Thus, the solid solution strength can be determined by the average concentration of the alloying elements in the matrix [11]:
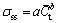 (5)
(5)
where σss is the solid solution strength, a and b are material constants, and 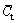 is the average concentration of alloying elements.
is the average concentration of alloying elements.
And 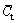 can be replaced by the volume fraction of precipitates, fr, for representation. Thus, the contribution of solid solution strength can be represented as follows:
can be replaced by the volume fraction of precipitates, fr, for representation. Thus, the contribution of solid solution strength can be represented as follows:
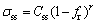 (6)
(6)
where Css is the equation coefficient and r is a material constant.
Thus, the overall strength can be expressed as follows:
σw=σi+σdis+σppt+σss (7)
where σw is the overall strength, and σi is the pure aluminium matrix strength. The corresponding schematic diagram of the relative contributions to strength is illustrated in Fig. 11.
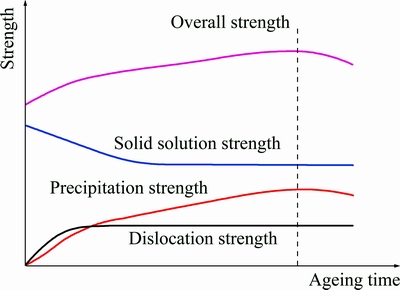
Fig. 11 Schematic diagram of relative contributions to strength
Hardness is an important factor that reflects the material properties and strength. Thus, in this section, hardness (H) is employed and expressed in the following form [14,26,27]:
H=Aσw+B (8)
where H is Vickers hardness, A is an equation coefficient and B is a material constant.
The strengthening model for AA6082 is mathematically assembled as follows:
 (9)
(9)
4.2 Determination of material constants
The genetic-algorithm (GA) tool is used to determine material constants. The model consists of ordinary differential equations, which are nonlinear and highly coupled. It is difficult to determine material constants using the traditional method. The genetic algorithm is based on the natural principle of ‘survival of the fittest’ to search the best value and it is also not critical for the selection of the initial values of material constants. Material constants are evaluated during a one-time search, and constants with low scores are eliminated. At the same time, constants with high scores are retained as the parental generation. The next generation is produced by the crossover and mutation of the parental generation. The search space and precision can be adjusted by setting various population sizes and generations. This method has a strong ability for global search and is suitable for solving multivalued optimization [19,28,29]. In terms of calculation efficiency, the data obtained from experimental cases (degree of deformation of 30% and strain rate of 0.01 s-1, degree of deformation of 30% and strain rate of 1 s-1, and degree of deformation of 0% and strain rate of 1 s-1) could be used to determine the material constants. The data obtained from the other experimental cases (degree of deformation of 30% and strain rate of 0.1 s-1, and degree of deformation of 10% and strain rate of 1 s-1) could be used for validation.
The objective function employed to determine material constants adopts the following form:
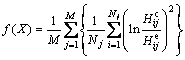 (10)
(10)
where X is the material constant to be optimized, X=(x1, x2, …, xs), s is the number of material constants, f(X) is the residual error of hardness, M is the number of tests, Nj is the number of data selected from the case j,  is the calculated value of the model for ageing time i, and
is the calculated value of the model for ageing time i, and  is the experimental value for ageing time i. The genetic-algorithm tool keeps searching different material constants to decrease the fitness value until it reaches the targeted precision. And then, the values for the material constants used in the model can be determined. The selected material constants optimised from the genetic-algorithm tool are illustrated in Table 2.
is the experimental value for ageing time i. The genetic-algorithm tool keeps searching different material constants to decrease the fitness value until it reaches the targeted precision. And then, the values for the material constants used in the model can be determined. The selected material constants optimised from the genetic-algorithm tool are illustrated in Table 2.
Table 2 Material constants for strengthening model of AA6082

4.3 Strengthening model validation
The material constants obtained from the genetic-algorithm optimization tool were input into the strengthening model in order to predict the hardness values of AA6082 for various cases. The calculated and experimental results are compared in Fig. 12.
Predictability can be evaluated by the Pearson correlation coefficient (R), average absolute relative error (EA), and root-mean-square error (ER), which are presented as follows:
 (11)
(11)
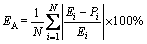 (12)
(12)
 (13)
(13)
where Ei is the experimental result, Pi is the model-calculated result, 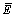 and
and 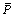 are the average values of the experimental and calculated results, and N is the number of data. R is generally used to reflect the degree of linear correlation between calculated and experimental results. EA and ER are used to reflect the error between calculated and experimental results. For this test, R, EA, and ER are 0.99402, 2.0054%, and 2.045, respectively, which indicates the good predictive ability of the AA6082 strengthening model.
are the average values of the experimental and calculated results, and N is the number of data. R is generally used to reflect the degree of linear correlation between calculated and experimental results. EA and ER are used to reflect the error between calculated and experimental results. For this test, R, EA, and ER are 0.99402, 2.0054%, and 2.045, respectively, which indicates the good predictive ability of the AA6082 strengthening model.
5 Numerical application
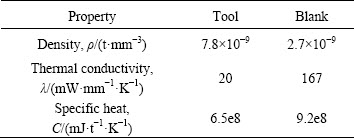
The cup drawing is traditionally used for analysis [30]. An FE model of a cup drawing with a flat bottom at elevated temperatures was established. The FE code ABAQUS was used. Figure 13 shows the schematic diagram of the geometric model with mesh, which is composed of the punch, die, holder and blank. The radius of the punch corner is 5 mm, the diameter of the punch is 50 mm, the radius of the die corner is 13 mm, and the diameter of the die cavity is 54.4 mm. The corresponding thermal and physical properties for the blank and tools are illustrated in Table 3 [28]. The strengthening model for AA6082 was programmed in FORTRAN and implemented into the main program of the FE software via the user-defined subroutine VUMAT. This enabled updates and modifications to the new user-defined state variables from the old state variables. The hardness value for every element at different times could be calculated and described graphically.
The FE model was established with the subroutine of the AA6082 strengthening model, and the material constants of AA6082 were determined before being used in this FE model. The cup was stamped to a set stroke without the occurrence of cracks. To simulate the hardness variation during the ageing process, an “ageing stage” was set after the “stamping stage”. The ageing period used normalized times, i.e., the ageing period was varied from “0” to “1”, where “0” indicates the start of ageing, and “1” indicates the end. The artificial ageing period was 9 h, which is consistent with the aforementioned research. The number of output steps was set to be 2200 for the ageing stage. In this numerical example, BHF was 2000 N, the punch velocity was 100 mm/s, the initial blank temperature was 500 °C, the friction coefficient was 0.15, and the punch stroke was 20 mm.

Fig. 12 Comparison of model-calculated and experimental results under various conditions

Fig. 13 Schematic diagram of geometric model with mesh used for hot cup drawing
Table 3 Thermal and physical properties for tools and blank used in FE model [28]
The simulated results for hardness distribution are shown in Fig. 14. A corresponding experimental cup after stamping and before ageing is presented in the right corner of Fig. 14(a). After deformation, the cup was cut into several slices and subjected to artificial ageing for different ageing times at the ageing temperature of 190 °C. Then, the hardness was measured. Figure 14(a) illustrates the simulated hardness distribution of the hot-stamped cup at the initial ageing step. Figure 14(b) demonstrates the hardness distribution at the ageing step 1100. Figure 14(c) shows the hardness distribution of the cup at ageing step 2200. Table 4 compares the FE-simulated and experimental hardness results. The hardness was measured at different positions of the hot-stamped and aged cup, namely, the bottom of the cup, the cup corner, the sidewall, and the flange. At the same time, the corresponding relative absolute errors between simulated and experimental results were calculated, indicating that the FE-simulated hardness values are in good agreement with the experimental ones.
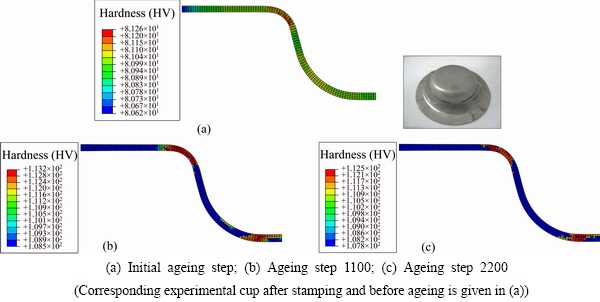
Fig. 14 Hardness distributions at different ageing steps
Table 4 Comparison of FE simulated hardness values with experimental ones for various ageing times

6 Conclusions
1) In terms of the HFQ technique used on the aluminium alloy AA6082, the strength of the workpiece increases with the increase of the degree of deformation and strain rate.
2) Hardness is enhanced by increasing ageing time during artificial ageing. It shows a sharp, initial rise and then increases gradually. When the ageing time is long, over-ageing occurs.
3) A strengthening model is established for AA6082 according to the strengthening mechanism, which consists of strain, strain rate, dislocations, volume fraction of precipitates, ageing time, and other factors. The model can predict and describe the variation in hardness of the part in different conditions, including underaged, peak-aged, and overaged periods. The Pearson correlation coefficient, average absolute relative error, and root-mean-square error between the calculated and experimental hardness results are 0.99402, 2.0054%, and 2.045, respectively.
4) The strengthening model can be implemented into ABAQUS via VUMAT to simulate the hardness distribution. The simulated and experimental results exhibit good agreement.
References
[1] JIANG F L, ZHANG H, WENG S C, FU D F. Characterization of dynamic microstructural evolution of AA7150 aluminum alloy at high strain rate during hot deformation [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 51-62.
[2] XIAO G, YANG Q W, LI L X. Modeling constitutive relationship of 6013 aluminum alloy during hot plane strain compression based on Kriging method [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 1096-1104.
[3] DONG G J, ZHAO C C, ZHAO J P, YA Y Y, CAO M Y. Research on technological parameters of pressure forming with hot granule medium on AA7075 sheet [J]. Journal of Central South University, 2016, 23: 765-777.
[4] MOGHANAKI S K, KAZEMINEIHAD M. Effects of non-isothermal annealing on microstructure and mechanical properties of severely deformed 2024 aluminum alloy [J]. Transactions of Nonferrous Metels Society of China, 2017, 27: 1-9.
[5] MA W Y, WANG B Y, FU L, ZHOU J, HUANG M D. Effect of friction coefficient in deep drawing of AA6111 sheet at elevated temperatures [J]. Transactions Of Nonferrous Metals Society of China, 2015, 25: 2342-2351.
[6] HUANG Y C, YAN X Y, QIU T. Microstructure and mechanical properties of cryo-rolled AA6061 Al alloy [J]. Transactions of Nonferrous Metals Society of China, 2015, 26: 12-18.
[7] FAN X B, HE Z B, YUAN S J, LIN P. Investigation on strengthening of 6A02 aluminum alloy sheet in hot forming-quenching integrated process with warm forming-dies [J]. Materials Science and Engineering A, 2013, 587: 221-227.
[8] FAN X B, HE Z B, YUAN S J, ZHENG K L. Experimental investigation on hot forming–quenching integrated process of 6A02 aluminum alloy sheet [J]. Materials Science and Engineering A, 2013, 573: 154-160.
[9] MA W Y, WANG B Y, YANG L, TANG X F, XIAO W C, ZHOU J. Influence of solution heat treatment on mechanical response and fracture behaviour of aluminium alloy sheets: An experimental study [J]. Materials & Design, 2015, 88: 1119-1126.
[10] YUAN S J, FAN X B, HE Z B. Hot forming-quenching integrated process with cold-hot dies for 2A12 aluminum alloy sheet [J]. Procedia Engineering, 2014, 81: 1780-1785.
[11] ZHANG J, DENG Y L, ZHANG X M. Constitutive modeling for creep age forming of heat-treatable strengthening aluminum alloys containing plate or rod shaped precipitates [J]. Materials Science and Engineering A, 2013, 563: 8-15.
[12] HO K C, LIN J G, DEAN T A. Constitutive modelling of primary creep for age forming an aluminium alloy [J]. Journal of Materials Processing Technology, 2004, 153-154: 122-127.
[13] LIU G, ZHANG G J, DING X D, SUN J, CHEN K H. Modeling the strengthening response to aging process of heat-treatable aluminum alloys containing plate/disc- or rod/needle-shaped precipitates [J]. Materials Science & Engineering A, 2003, 344: 113-124.
[14] POOLE W J,  J A, SKJERVOLD S, WATERLOO G. A model for predicting the effect of deformation after solution treatment on the subsequent artificial aging behavior of AA7030 and AA7108 alloys [J]. Metallurgical and Materials Transactions A, 2000, 31: 2327-2338.
J A, SKJERVOLD S, WATERLOO G. A model for predicting the effect of deformation after solution treatment on the subsequent artificial aging behavior of AA7030 and AA7108 alloys [J]. Metallurgical and Materials Transactions A, 2000, 31: 2327-2338.
[15] ESMAEILI S, LLOYD D J. Modeling of precipitation hardening in pre-aged AlMgSi(Cu) alloys [J]. Acta Materialia, 2005, 53: 5257-5271.
[16] HOU Y H, GU Y X, LIU Z Y, LI Y T, CHEN X. Modeling of whole process of ageing precipitation and strengthening in Al-Cu-Mg-Ag alloys with high Cu-to-Mg mass ratio [J]. Transactions of Nonferrous Metals Society Of China, 2010, 20: 863-869.
[17] ZHOU J, WANG B Y, HUANG M D, CUI D. Effect of hot stamping parameters on the mechanical properties and microstructure of cold-rolled 22MnB5 steel strips [J]. International Journal of Minerals, Metallurgy, and Materials, 2014, 21: 544-555.
[18] MOHAMED M S. An investigation of hot forming cold die quench of AA6082 aluminum alloys [D]. London: Imperial College, 2010.
[19] MOHAMED M S, FOSTER A D, LIN J G, BALINT D S, DEAN T A. Investigation of deformation and failure features in hot stamping of AA6082: Experimentation and modelling [J]. International Journal of Machine Tools and Manufacture, 2012, 53: 27-38.
[20] FAN X B, HE Z B, ZHOU W Y, YUAN S J. Formability and strengthening mechanism of solution treated Al-Mg-Si alloy sheet under hot stamping conditions [J]. Journal of Materials Processing Technology, 2016, 228: 179-185.
[21] SHI L, YANG H, GUO L G, ZHANG J. Constitutive modeling of deformation in high temperature of a forging 6005A aluminum alloy [J]. Materials & Design, 2014, 54: 576-581.
[22] LI L T, LIN Y C, ZHOU H M, JIANG Y Q. Modeling the high-temperature creep behaviors of 7075 and 2124 aluminum alloys by continuum damage mechanics model [J]. Computational Materials Science, 2013, 73: 72-78.
[23] GARRETT R, LIN J G, DEAN T. An investigation of the effects of solution heat treatment on mechanical properties for AA 6xxx alloys: Experimentation and modelling [J]. International Journal of Plasticity, 2005, 21: 1640-1657.
[24] ROY M J, MAIJER D M, DANCOINE L. Constitutive behavior of as-cast A356 [J]. Materials Science and Engineering A, 2012, 548: 195-205.
[25] ZHANG P, YE L Y, ZHANG X M, GU G, JIANG H C, WU Y L. Grain structure and microtexture evolution during superplastic deformation of 5A90 Al-Li alloy [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 2088-2093.
[26] MYHR O R, GRONG 
 H G, MARIOARA C D. Modelling of the microstructure and strength evolution in Al-Mg-Si alloys during multistage thermal processing [J]. Acta Materialia, 2004, 52: 4997-5008.
H G, MARIOARA C D. Modelling of the microstructure and strength evolution in Al-Mg-Si alloys during multistage thermal processing [J]. Acta Materialia, 2004, 52: 4997-5008.
[27] GRONG  SHERCLIFF H R. Microstructural modelling in metals processing[J]. Progress In Materials Science, 2002, 47: 163-282.
SHERCLIFF H R. Microstructural modelling in metals processing[J]. Progress In Materials Science, 2002, 47: 163-282.
[28] MA W Y, WANG B Y, BIAN J H, TANG X F, YANG L, HUO Y M. A new damage constitutive model for thermal deformation of AA6111 sheet [J]. Metallurgical and Materials Transactions A, 2015, 46: 2748-2757.
[29] LIN J G. A review on damage mechanisms, models and calibration methods under various deformation conditions [J]. International Journal of Damage Mechanics, 2005, 14: 299-319.
[30] MA W Y, WANG B Y, FU L, ZHOU J, HUANG M D. Influence of process parameters on deep drawing of AA6111 aluminum alloy at elevated temperatures [J]. Journal of Central South University, 2015, 22: 1167-1174.
热成形工艺参数对AA6082铝合金性能的影响
马闻宇1,王宝雨1,林建国1,2,唐学峰1
1. 北京科技大学 机械工程学院,北京 100083;
2. Department of Mechanical Engineering, Imperial College London, London SW7 2AZ, UK
摘 要:基于铝合金热冲压工艺,通过热物理模拟实验的方法,研究了工艺参数对AA6082铝合金力学性能的影响规律。利用透射电子显微镜分析了强化相分布和强化机理,建立了针对AA6082铝合金热冲压工艺的形变强化新模型,并通过遗传算法工具箱确定了模型中的材料常数。该模型可以预测不同工况下材料性能的演化行为,得到AA6082铝合金形变强化模型预测值与实验值的Pearson相关系数为0.99402、平均相对误差为2.0054%、均方根误差为2.045,说明预测度很好。将模型二次开发入有限元仿真软件ABAQUS中,从而实现对铝合金热冲压杯形件在不同时效条件下性能的预测。
关键词:铝合金AA6082;力学性能;强化模型;热成形
(Edited by Bing YANG)
Foundation item: Project (P2014-15) supported by the State Key Laboratory of Materials Processing and Die and Mould Technology, Huazhong University of Science and Technology, China; Project (20120006110017) supported by the Specialized Research Fund for the Doctoral Program of Higher Education of China; Project (2015M580977) supported by China Postdoctoral Science Foundation; Project supported by Beijing Laboratory of Metallic Materials and Processing for Modern Transportation, China
Corresponding author: Bao-yu WANG; Tel/Fax: +86-10-82375671; E-mail: bywang@ustb.edu.cn
DOI: 10.1016/S1003-6326(17)60272-3
Abstract: The influences of process parameters on mechanical properties of AA6082 in the hot forming and cold-die quenching (HFQ) process were analysed experimentally. Transmission electron microscopy was used to observe the precipitate distribution and to thus clarify strengthening mechanism. A new model was established to describe the strengthening of AA6082 by HFQ process in this novel forming technique. The material constants in the model were determined using a genetic algorithm tool. This strengthening model for AA6082 can precisely describe the relationship between the strengths of formed workpieces and process parameters. The predicted results agree well with the experimental ones. The Pearson correlation coefficient, average absolute relative error, and root-mean-square error between the calculated and experimental hardness values are 0.99402, 2.0054%, and 2.045, respectively. The model is further developed into an FE code ABAQUS via VUMAT to predict the mechanical property variation of a hot-stamped cup in various ageing conditions.


