J. Cent. South Univ. (2020) 27: 132-143
DOI: https://doi.org/10.1007/s11771-020-4283-4
Process simulation and optimization of flow field in wet electrostatic precipitator
YE Xing-lian(叶兴联)1, 2, WANG Shuai(王帅)2, ZHANG Hao(张浩)1, AN Xi-zhong(安希忠)1,GUO Bao-yu(郭宝玉)3, LI Li-feng(李立锋)2
1. Key Laboratory for Ecological Metallurgy of Multimetallic Mineral of Ministry of Education, School of Metallurgy, Northeastern University, Shenyang 110819, China;
2. State Environmental Protection Engineering Center for Power Industrial Dust Control,Longyan 364000, China;
3. Department of Chemical Engineering, Monash University, Clayton VIC 3800, Australia
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract:
To improve the dust removal performance of the wet electrostatic precipitator (WESP), a flow field optimization scheme was proposed via CFD simulation in different scales. The simplified models of perforated and collection plates were determined firstly. Then the model parameters for the resistance of perforated and collection plates, obtained by small-scale flow simulation, were validated by medium-scale experiments. Through the comparison of the resistance and velocity distribution between simulation results and experimental data, the simplified model is proved to present the resistance characteristics of perforated and collection plates accurately. Numerical results show that after optimization, both the flow rate and the pressure drop in the upper room of electric field regions are basically equivalent to those of the lower room, and the velocity distribution in flue inlet of WESP becomes more uniform. Through the application in practice, the effectiveness and reliability of the optimization scheme are proved, which can provide valuable reference for further optimization of WESP.
Key words:
Cite this article as:
YE Xing-lian, WANG Shuai, ZHANG Hao, AN Xi-zhong, GUO Bao-yu, LI Li-feng. Process simulation and optimization of flow field in WESP [J]. Journal of Central South University, 2020, 27(1): 132-143.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-020-4283-41 Introduction
As an effective and popular dust removal equipment in industry, the electrostatic precipitator (ESP) has been widely used in thermal power plants due to its advantages like high collection efficiency, low resistance loss, high operation temperature, great amount of processing gas, and high automatic level [1-4]. Actually, there are mainly two types of ESPs depending on dust-cleaning modes, namely dry electrostatic precipitator (dry-ESP) and wet electrostatic precipitator (WESP) [5-7]. Compared with dry-ESP, WESP has higher removal efficiency for dust that not only has high specific resistance, high humidity and high temperature, but also is inflammable and explosive. Furthermore, water vapor and some poisonous and harmful gas pollutants can also be removed from the flue gas synchronously [8-11]. Therefore, WESP exhibits promising prospect in both scientific research and engineering applications.
In the operating process of WESP, collection plates need to be cleaned regularly. During maintenance, the corresponding device should be powered off, resulting in the flue gas in this area passing through without any treatments. However, the national and local emission standards of the flue gas must be satisfied and thus other electric field regions that are unwashed need to have high collection efficiency to take the additional job.
Previous studies indicated that there are many factors that can influence the performance of the dust removal performance of WESP. For example, SAIYASITPANICH et al [12] evaluated the performance of a tubular single-stage WESP for the removal of number-based DPM emissions and found that the variation of gas residence time within the WESP from around 0.1 s to around 0.4 s can lead to a substantial increase in the collection efficiency from 67% to 96%. CHANG et al [13] explored the relationships between efficiency and velocity, electrode material, discharge electrode shape in WESP and the optimal operating parameters were determined. CHEN et al [14] introduced the fine water mist at the room temperature to enhance the collection efficiency of nanoparticles in WESP and the experimental results show that the maximum nanoparticle collection efficiency is improved from 92.9% to 99.7% by using this method. YANG et al [15] studied the removal efficiency of fine particles in WESP under the pre-charged condition and found that the effective migration velocities for PM 0.1, PM 1.0 and PM 2.5 increased by 69.9%, 65.7% and 34.2%, respectively, with the assistance of the pre-charger. In addition, they evaluated the effects of two key parameters including electrical characteristics and gas loading on SO3 removal efficiency under severe corona suppression conditions and found that by using proper electrode configurations and lower velocity under a pilot plant condition, the removal efficiency of SO3 can be higher than 90% [16]. However, it is necessary to ensure the uniformity of the flow field before adjusting other operation parameters to improve the dust removal performance of WESP. QIU et al [17] modeled the velocity profile in ESP for four conditions under the self-similarity principle and found that the dust removal efficiency can be obviously improved by optimizing the flow field. HAQUE et al [18] studied the influence of the velocity profile at the inlet boundary on the uniformity of the flow field inside an ESP by numerical simulations. TU et al [19] built a laboratory-scale hybrid particulate collector to investigate the effect of perforated plates (with different percentages of open area and opening types) on the flow field and found that the openings facilitate particle deposition on the flank and back sides. Generally speaking, the flow field optimization devices include guiding and perforated plates, and the latter is commonly used to optimize the flow field in WESP. Some researchers have studied the optimization effect of perforate plates on flow field by experimental method that is operational complexity. And the cost of trial and error is very high, which is not feasible in engineering. The numerical simulation method has also been adopted by some researchers. However, in large-scale ESP, the perforate plates contain countless small holes resulting in incalculable grids which need huge computing resource.
The aim of this study is to optimize the flow field of ESP by adding perforated plates based on CFD. In order to solve the problem of high cost by experimental means only and the difficulty in meshing of perforate plates in large-scale ESP by numerical simulation, a research scheme which is low cost and high precision was proposed in this work. Due to the extreme complexity of the perforated plate containing millions of micro-holes, a simplified model is usually adopted in both previous studies [20, 21] and current work. It is worthwhile mentioning that the parameters of the simplified model of perforated plates are obtained by small-scale numerical simulation in which the number of grids is within a reasonable range and then validated by medium-scale experiments. Finally, the validated model is used for the flow field optimization of WESP. The research scheme is shown in Figure 1.
2 Geometric model and governing equations
2.1 Geometric model
According to the structure of WESP for 300 MW units in a power plant, the geometric model of WESP unit is established. The WESP unit with mesh division is shown in Figure 2. The mesh number is 2.4 million. And all the meshes satisfy the requirement of equi-size skew < 0.97 after mesh checking. Here, the cross section of the inlet flue is circular with the radius of 7.675 m; the cross section of the outlet flue is 9 m×5.8 m; and the cross section of the electric field of upper room and lower room is 16.73 m×10 m. The calculation domain is meshed by structured and unstructured grids. Since the pressure is the key parameter in this work, the pressure drop at the inlet and outlet of the WESP unit is selected as a reference value for grid independence verification in this work. Figure 3 shows the pressure drop at the inlet and outlet of the WESP unit with different mesh numbers under a fixed working condition. It can be seen that when the number of grids is greater than 6.8 million, the pressure drop at the inlet and outlet basically almost keeps the same. Therefore, the gird number of 6.8 million is adopted for calculation of numerical simulation.
Figure 1 Research scheme of this work
Figure 2 WESP unit mesh
Figure 3 Pressure drop as a function of grid number
In our simulations, the air flow in the inlet section is assumed to be evenly distributed and the direction is perpendicular to the inlet section. Velocity-inlet is utilized at the inlet boundary. Pressure-out is used at the outlet boundary. Non-slip wall is adopted as the wall condition of the solid wall and guiding plates. Porous-jump model is applied to define the boundary conditions of perforated and collection plates in ESP unit, and the specific model parameters are calculated according to different orifice ratios. It should be noted that there are no grids of perforated and collection plates in the WESP unit mesh. The effects of perforated and collection plates on the flow field are reflected by the porous-jump model.
2.2 Governing equations
The incompressible and steady Navier-Stokes equations are adopted to solve the problem for gas flow. In order to improve the accuracy of solution, the turbulence flow in perforated plates and collection plates, which belongs to near-wall flow, is solved by k-ω model [22]. And the turbulence flow in the WESP unit is solved by the standard k-ε model. Governing equations include mass conservation equation and momentum conservation equation, which can be written as [23, 24]:
(1)
(2)
The k-ω equation can be expressed as [25]:
(3)
(4)
The k-ε equation can be written as [26]:
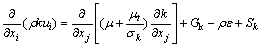(5)
(6)
where ρg is gas density; u is gas velocity; τg is gas stress; p is gas pressure; g is acceleration of gravity; Sm is the term of momentum equation; Sk, Sω and Sε are source term of turbulent kinetic energy k, ω and ε caused by particle motion, respectively; μ is gas dynamic viscosity coefficient; the turbulent viscosity μt is expressed as a function of k and ε using
with the eddy viscosity concept built by Boussinesq; the empirical constant Cμ equals 0.09 in general [27, 28]; β is set to be 0.075; the turbulent viscosity μT can be expressed as a function of k and ω using ω; Gk is turbulent kinetic energy generation rate; σε, σω and σk are Prandtl number of k, ω and ε.
3 Experimental setup
Figure 4 shows the experimental model of the WESP used in this study which is 1/10 the actual one. By measuring the velocity at different monitoring surfaces, the flow distribution between upper and lower electric field area and the uniformity of velocity distribution in the flue and electric field are obtained. The specific monitoring surfaces are shown in Figure 5. As long as the air leakage rate of physical model is less than 2%, the reliability of experimental data can be guaranteed.
Figure 4 Experimental model of WESP
Figure 5 Monitoring surfaces of model (A-Flue inlet; B1-Upper flue inlet; B2-Lower flue inlet; C1-Upper electric field section; C2-Lower electric field section; D1-Upper flue outlet; D2-Lower flue outlet; E-Flue outlet)
The flow assignment △α and the uniformity σr of velocity distribution are calculated by Eqs. (7) and (8), respectively.
(7)
(8)
where △α is the relative deviation value of gas flow rate; Qi is the gas flow rate of the branch flue; 
is the average gas flow rate; σr is the relative root mean square error of velocity distribution; vi is the velocity of monitoring point; n is the number of monitoring points in the section.
4 Results and discussion
4.1 Small-scale simulation
As mentioned above, perforated plates used to make flow field uniform in the WESP are composed of tens of thousands of unit cells, which means that direct modelling on the perforated plates may not be feasible. Therefore, it is necessary to simplify the perforated plate equivalently. The perforated plates can be regarded as a porous medium with finite thickness and directional permeability. The pressure drop △pp caused by the perforated plates can be expressed as the sum of the viscous loss term and the inertia loss term [29, 30].
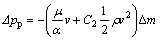(9)
where α is the permeability of perforated plates,
; C2 is the pressure loss coefficient per unit perforated plate thickness, 
; v is the velocity component perpendicular to the perforated plates; △m is the thickness of the perforated plates; d is the aperture; b1 and b2 depend on the porosity; f is the opening percentage. By setting different parameters of v, d, △m and f in numerical simulation, the values of α and C2 can be calculated.
In addition, the relationship between the orifice ratio and the pressure drop is concerned in the simulation verification and engineering application. Figure 6 shows the curves of pressure drop variation with velocity in different orifice ratios. When the air passes through the perforated plate, the pressure drops at the area where reflux comes into being, indicating that the reflux at the downstream of the perforated plate causes the pressure loss. And also it can be seen from Figure 6 that the pressure drop increases with the increase of the velocity, and the smaller the orifice ratio is, the greater is the pressure drop.
The collection plates in WESP are not completely flat, and there is always a resistance due to the friction between the air and the collection plates. Considering the number of collection plates in the WESP is large, the resistance produced by them cannot be ignored. And through preliminary simulation, it is found that the resistance △pc caused by the collection plates is basically linear with the length of the plate and can be expressed as:
(10)
where l is the length of the single collection plate; χ is the resistance coefficient of the collection plate; C is the constant. By setting different collection plate lengths l, the parameter χ can be obtained.
Figure 6 Pressure drop changing with velocity in different orifice ratios
Figure 7 shows the fitting curve of the pressure drop changing with the length of the collection plate. As can be seen that the motion direction of airflow changes at two ends of the collection plate. And there is an obvious pressure drop area when the air flows through two ends of the collection plate. By using regression analysis, follow formula can be obtained: Δpc=0.55l+1.9067 and R2=0.9817.
4.2 Simplified model verification
To determine whether the simplified model conforms to the resistance characteristics of the perforated and collection plates, the parameters of Porous-jump model determined by the simplified model is used to represent the resistance of the perforated and collection plates in the numerical simulation of the ESP unit. Meanwhile, corresponding experiments at the same scale are also carried out. Through comparison between the data collected from both physical experiments and the numerical simulations, the reliability of the model can be verified.
Figure 7 Pressure drop as function of length of collection plate
4.2.1 Comparison of total pressure
A fixed number of monitoring points are evenly arranged in the monitoring surface of the flue and the electric field to obtain the flow field information of a specific space point. The total pressure in a monitoring surface is obtained by calculating the mean total pressure of the monitoring points on it. Figure 8 shows the comparison of the total pressure at different monitoring surfaces between simulation and experiment, where A, B, C and D represent, respectively, the monitoring surfaces of the flue inlet, upper and lower inlets of the branch flue, upper and lower sections of the electric field, and upper and lower outlets of the branch flue. The total pressure at surface A is set to 0 for the sake of clear comparison. It can be seen from Figure 8 that the trend of the numerical results is consistent with the experimental data at different monitoring surfaces, which indicates that the simplified model utilized in our numerical simulations is effective in modelling practical cases.
4.2.2 Comparison of velocity distribution
The measured velocities at different monitoring points in our physical experiments are also compared with the simulation results, as shown in Figures 9 and 10. It needs to note that considering the influence of flow fluctuation and experimental error, the experimental data are expressed in the form of error lines from repeated experiments. The results in Figures 9 and 10 demonstrate that the data from experiments have good agreement with those from numerical simulations, which proves the robustness and effectiveness of the simplified model utilized.
Figure 8 Comparison of total pressure at different monitoring surfaces
By calculation, the flow assignment △α and velocity distribution uniformity σr in the flue inlet and the electric field section are given in Table 1. One can find that the values of △α and σr from the simulation results basically match with those from physical experiments with slight difference between them, which indicates that the simplified model can satisfactorily reflect the resistance characteristics of the perforated and collection plates.
4.3 Optimization design of flow field
The flow field of WESP is optimized by adding perforated plates in the flue and electric field area. And the feasibility of the optimization scheme is evaluated by numerical simulation. In addition, the optimization design should make the flow field satisfy the requirements of △α<5% and σr<0.2.
4.3.1 Flow field optimization of flue inlet
The streamlines and velocity distributions in the flue section before and after optimization are shown in Figures 11 and 12. From the figures one can find that before optimization, there is a large range of vortex at upstream position of the flue branch, and the gas basically passes into the WESP through upper area of the flue, which affects the removal performance of the WESP. After installing guiding plates, the velocity distribution in the flue is more uniform, and the vortex at upstream position of the flue branch disappears basically. By comparing the values (as shown in Table 2) of △α and σr before and after optimization, one can find that the values of △α and σr after optimization are in a reasonable range.
4.3.2 Flow field optimization of electric field
The velocity distribution in the electric field is directly affected by the orifice ratio. Due to the pressure drop correlation with the orifice ratio as shown in Figure 6, the orifice ratio of the high-velocity region in surface section should be set higher to make the velocity distribution on the whole section more uniform. Figure 13 shows the mean velocity in different heights of the upper and lower electric field section before and after optimization and corresponding orifice ratio. And the contours of the velocity distributions in electric field section before and after optimization are given in Figure 14. The comparison between them indicates that the flow field becomes more uniform after optimization. By calculation, the local maximum velocity in the electric field section reaches 4.87 m/s before optimization, and the relative root mean square difference between upper and lower rooms is 0.321 and 0.335, both of which are higher than the pre-designed value of 0.2. This will restrict the removal performance of the WESP.
Figure 9 Velocity distributions at different monitoring points in monitoring surface of flue inlet (values of velocities are obtained from both physical experiments and numerical simulations):
Figure 10 Velocity distributions at different monitoring points in monitoring surface of electric field (values of velocities are obtained from both physical experiments and numerical simulations):
Table 1 Flow assignment and velocity distribution uniformity
Figure 11 Streamline profile of flue inlet:
Figure 12 Velocity distribution in flue inlet:
Table 2 Flow distribution and uniformity of velocity distribution before and after optimization
And after changing orifice ratio, the local maximum velocity is 3.5 m/s which is obviously reduced, and the relative root mean square difference between upper and lower rooms is 0.179 and 0.175, respectively, which meet the design requirements.
Figure 15 gives the pressure drop in monitoring surfaces before and after optimization. As can be seen that after optimization, the pressure drop curve of the upper room fits well with that of the lower room. Therefore, the flow assignment influenced by the pressure drop will become more uniform between the two rooms. And by contrast of the pressure drop at the B monitoring surface which represents the flue inlet in Figures 15(a) and (b), one can find that the pressure drop in lower room of the flue inlet is obviously reduced after optimization, this is because the vortex disappears after adding perforated plates, which contributes to the uniformity of velocity distribution of the flow field. Therefore, via simulation analysis, the optimization scheme is proved to be feasible.
The optimization scheme is applied to an actual engineering project. The flow assignment △α and velocity distribution uniformity σr of the field test data are calculated and compared with simulation results, as shown in Table 3. It can be seen that the flow assignment △α of the field test data is less than 5%, and the velocity distribution uniformity σr is less than 0.2. Both of them are within the pre-designed value, implying that the optimization scheme is successful, and the simulation results are in good agreement with the field data, which indicates that the simplified model is in line with engineering practice.
Figure 13 Velocity distributions and corresponding orifice ratio variation in different electric field section position before and after optimization:
Figure 14 Velocity distributions in electric field section before and after optimization:
Figure 15 Pressure drop in monitoring surfaces before and after optimization:
Table 3 Flow assignment and velocity distribution uniformity of simulation results and field test data
5 Conclusions
Aiming at optimizing the flow field of WESP by perforated plates in engineering, a simplified model is adopted. The model parameters are determined by numerical simulation and verified by the experiment. Through practical application, the following conclusions can be obtained.
1) The simplified model can reflect the influence of perforated and collection plates on total pressure and velocity distribution in WESP.
2) The orifice ratio designed according to velocity distribution is better than single orifice ratio. And the local maximum velocity decreased from 4.87 m/s to 3.5 m/s.
3) The combination of guiding and perforated plates in the WESP not only makes the vortex disappear in the flue, but also makes the flow rate of the branch flues and velocity distribution in the WESP more uniform. Both the values of △α and σr satisfy the pre-designed requirement.
4) Through the engineering practice, it is proved that the optimization scheme from the verified numerical simulation using simplified model is feasible, which saves research cost and providing meaningful guidance for engineering application.
References
[1] SWIERCZOK A, JEDRUSIK M. The collection efficiency of ESP model-comparison of experimental results and calculations using deutsch model [J]. Journal of Electrostatics, 2018, 91: 41-47. DOI: 10.1016/j.elstat.2017. 12.004.
[2] LI X D, ZHOU C Y, LI J W, LU S Y, YAN J H. Distribution and emission characteristics of filterable and condensable particulate matter before and after a low-low temperature electrostatic precipitator [J]. Environmental Science and Pollution Research, 2019, 26: 13. DOI: 10.1007/ s11356-019-04570-y.
[3] TANSKI M, BERENDT A, MIZERACZYK J. Closed SDBD-driven two-stage electrostatic precipitator [J]. Journal of Cleaner Production, 2019, 226: 74-84. DOI: 10.1016/ j.jclepro.2019.03.280.
[4] KAWADA Y, SHIMIZE H. Development of an electrostatic precipitator with porous carbon electrodes to collect carbon particles [J]. Energies, 2019, 12(14): 2805. DOI: 10.3390/ en12142805.
[5] BORDADO M J, QUINTAFERREIRA J C, QUINTA- FERREIRA R M. Treatment and use of air pollution control residues from MSW incineration: An overview [J]. Waste Management, 2008, 28(11): 2097-2121. DOI: 10.1016/ j.wasman.2007.08.030.
[6] McCANN D. New and upgradedelectrostaticprecipitators for recovery boilers [J]. Journal of Science & Technology for Forest Products and Processes, 2017, 6(3): 15-18.
[7] PARK H W, PARK D W. Removal kinetics for gaseous NO and SO2 by an aqueous NaClO2 solution mist in a wet electrostatic precipitator [J]. Environmental Technology Letters, 2017, 38(7): 835-843. DOI: 10.1080/09593330.2016. 1213770.
[8] SAIYASITPANICH P, KEENER T C, LU M M, LIANG F Y, KHANG S J. Control of diesel gaseous and particulate emissions with a tube-type wet electrostatic precipitator [J]. Journal of the Air & Waste Management Association, 2008, 58(10): 1311-1317.
[9] SU L P, DU Q, WANG Y D, DONG H M, GAO J M, WANG M, DONG P. Purification characteristics of fine particulate matter treated by a self-flushing wet electrostatic precipitator equipped with a flexible electrode [J]. Journal of the Air & Waste Management Association, 2018, 68(7): 725-736. DOI: 10.1080/10962247.2018. 1460635.
[10] YANG Z D, ZHENG C H, ZHANG X F, CHANG Q Y, WENG W G, WANG Y, GAO X. Highly efficient removal of sulfuric acid aerosol by a combined wet electrostatic precipitator [J]. RSC Advances, 2018, 8(1): 59-66.
[11] CAO R J, TAN H Z, XIONG Y Y, MIKULCIC H, VUJANOVIC M, WANG X B, DUIC N. Improving the removal of particles and trace elements from coal-fired power plants by combining a wet phase transition agglomerator with wet electrostatic precipitator [J]. Journal of Cleaner Production, 2017, 161: 1459-1465. DOI: 10.1039/C7RA11520B
[12] SAIYASITPANICH P, KEENER T C, LU M M, KHANG S J, EVANS D E. Collection of ultrafine diesel particulate matter (DPM) in cylindrical single-stage wet electrostatic precipitators [J]. Environmental Science & Technology, 2006, 40(24): 7890-7894. DOI: 10.1021/es060887k.
[13] CHANG J, DONG Y, YAN J, LI B, MA C Y. Performance test of a new wet ESP with flexible collection Electrodes [C]// International Conference on Bioinformatics & Biomedical Engineering. IEEE, 2010. DOI: 10.1109/ ICBBE.2010. 5516443.
[14] CHEN T M, TSAI C J, YAN S Y, LI S N. An efficient wet electrostatic precipitator for removing nanoparticles, submicron and micron-sized particles [J]. Separation & Purification Technology, 2014, 136: 27-35. DOI: 10.1016/ j.seppur.2014.08.032.
[15] YANG Z D, ZHENG C H, LIU S J, GUO Y S, LIANG C S, WANG Y, HU D Q, GAO X. A combined wet electrostatic precipitator for efficiently eliminating fine particle penetration [J]. Fuel Processing Technology, 2018, 180: 122-129. DOI: 10.1016/j.fuproc.2018.08.013.
[16] YANG Z D, ZHENG C H, ZHANG X F, ZHOU H, SILVA A A, LIU C Y, SNYDER B, WANG Y, GAO X. Challenge of SO3 removal by wet electrostatic precipitator under simulated flue gas with high SO3 concentration [J]. Fuel, 2018, 217: 597-604. DOI: 10.1016/j.fuel.2017.12.125.
[17] QIU Z Z, LI P, PAN W G, REN J X, WANG W H, WU J, ZHU Q Z. Modeling of the velocity profile and experimental study on velocity uniformity in the electrostatic precipitator [C]// International Conference on Power Engineering. Hangzhou, 2007. DOI: 10.1007/ 978-3-540-76694-0_85.
[18] HAQUE S M E, RASUL M G, KHAN M M K, DEEV A V, SUBASCHANDAR N. Influence of the inlet velocity profiles on the prediction of velocity distribution inside an electrostatic precipitator [J]. Experimental Thermal and Fluid Science, 2009, 33(2): 322-328. DOI: 10.1016/j.expthermflusci.2008.09.010.
[19] TU G, SONG Q, YAO Q. Experimental and numerical study of particle deposition on perforated plates in a hybrid electrostatic filter precipitator [J]. Powder Technology, 2017, 321: 143-153. DOI: 10.1016/j.powtec.2017.08.021.
[20] YE X L, SU Y B, GUO B Y, YU A B. Multi-scale simulation of the gas flow through electrostatic precipitators [J]. Applied Mathematical Modelling, 2016, 40(21, 22): 9514-9526. DOI: 10.1016/j.apm.2016.06.023.
[21] GUO B Y, YANG S Y, XING M, DONG K J, YU A B, GUO J. Toward the development of an integrated multiscale model for electrostatic precipitation [J]. Industrial & Engineering Chemistry Research, 2013, 52(33): 11282-11293. DOI: 10.1021/ie303466g.
[22] GUO B Y, HOU Q F, YU A B, LI L F, GUO J. Numerical modelling of the gas flow through perforated plates [J]. Chemical Engineering Research & Design, 2013, 91(3): 403-408. DOI: 10.1016/j.cherd.2012.10.004.
[23] LUO K, LI Y, ZHENG C H, GAO X, FAN J R. Numerical simulation of temperature effect on particles behavior via electrostatic precipitators [J]. Applied Thermal Engineering, 2015, 88: 127-139. DOI: 10.1016/j.applthermaleng.2014. 11.078.
[24] YANG K, LI Q, DING Z J, XIAO L C. CFD-based simulation study on producer gas explosion in an electrostatic precipitation [J]. Process Safety Progress, 2016, 35(1): 96-102. DOI: 10.1002/prs.11743.
[25] GAO F D,WANG D X,WANG H D. Numerical analysis and verification of the gas jet from aircraft engines impacting a jet blast deflector [J]. Chinese Journal of Mechanical Engineering, 2018, 31(1): 86. DOI: CNKI:SUN:YJXB. 0.2018-05-013.
[26] LEE S D. Impacts of surrounding building layers in CFD wind simulations [J]. Energy Procedia, 2017, 122: 50-55. DOI: 10.1016/j.egypro.2017.07.313.
[27] CHOI B S, FLETCHER C A J. Computation of particle transport in an electrostatic precipitator [J]. Journal of Electrostatics, 1997, 40-41: 413-418. DOI: 10.1016/ s0304-3886(97)00080-6.
[28] SKODRAS G, KALDIS S P, SOFIALIDIS D, FALTIS O, GRAMMELIS P, SAKELLAROPOULOS G P. Particulate removal via electrostatic precipitators-CFD simulation [J]. Fuel Processing Technology, 2006, 87(7): 623-631.
[29] TU J H, YUAN W F, ZHU P J. Computation of flow field distribution in electrostatic precipitator equal resistance simulation [J]. Journal of Environmental Engineering, 2004, 28: 37-39.
[30] SAHIN B. Pressure losses in an isolated perforated plate and jets emerging from the perforated plate [J]. International Journal of Mechanical Sciences, 1989, 31: 51-61. DOI: 10.1016/0020-7403(89)90118-5.
(Edited by HE Yun-bin)
中文导读
湿式静电除尘器流场的过程模拟及优化
摘要：为了提高湿式静电除尘器的除尘性能，本文提出了一种基于多尺度数值模拟的流场优化方法。首先, 确定多孔板和收尘板的简化模型；然后，得到相关的阻力参数，并通过中尺度实验进行验证。将模拟得到的阻力和速度分布与实验数据比较后发现简化模型能够准确地反映多孔板和收尘板的阻力特性。数值结果表明，经过优化后，电场上、下室的流量和压降基本相当，且烟道入口的速度分布更加均匀。将优化方案应用于工程实际后发现该方案确实有效可靠，可为湿式静电除尘器的性能优化提供有价值的参考。
关键词：过程模拟；优化；流场；湿式静电除尘器；多孔板；收尘板
Received date: 2019-01-17; Accepted date: 2019-09-03
Corresponding author: ZHANG Hao, PhD, Professor; Tel: +86-24-83687506; E-mail: zhangh@mail.neu.edu.cn; AN Xi-zhong, PhD, Professor; E-mail: anxz@mail.neu.edu.cn; ORCID: 0000-0003-4287-6767
Abstract: To improve the dust removal performance of the wet electrostatic precipitator (WESP), a flow field optimization scheme was proposed via CFD simulation in different scales. The simplified models of perforated and collection plates were determined firstly. Then the model parameters for the resistance of perforated and collection plates, obtained by small-scale flow simulation, were validated by medium-scale experiments. Through the comparison of the resistance and velocity distribution between simulation results and experimental data, the simplified model is proved to present the resistance characteristics of perforated and collection plates accurately. Numerical results show that after optimization, both the flow rate and the pressure drop in the upper room of electric field regions are basically equivalent to those of the lower room, and the velocity distribution in flue inlet of WESP becomes more uniform. Through the application in practice, the effectiveness and reliability of the optimization scheme are proved, which can provide valuable reference for further optimization of WESP.
