基于有限单元法的裂纹梁结构疲劳寿命预测模型-有色金属在线

纹梁结构的疲劳寿命，提出一种裂纹梁结构的振动与疲劳裂纹扩展耦合分析方法。首先，基于有限单元法建立裂纹梁结构的动力学模型；然后，根据裂纹梁单元的特点，推导裂纹梁单元的应力强度因子表达式，在此基础上应用Walker方程建立疲劳裂纹扩展增量计算式，再基于振动响应与裂纹扩展循环同步分析法，计算疲劳裂纹扩展寿命；基于该疲劳寿命预测模型，分析激振频率、激振力幅值和应力比对裂纹梁疲劳寿命的影响；最后，对裂纹梁进行疲劳试验，将试验测量结果与模型计算结果进行比较，验证所提出模型的准确性。研究结果表明：提出的疲劳寿命预测模型较好地表征了疲劳裂纹扩展寿命与其结构参数之间的内在关系，反映了振动对裂纹梁结构疲劳寿命的影响；随着激振频率接近固有频率，裂纹扩展速率增大，裂纹梁的疲劳寿命明显降低；随着激振力幅值增大，裂纹梁的应力强度因子幅增大，疲劳裂纹扩展寿命降低；随着应力比增加，裂纹梁的疲劳寿命显著提高。

关键词:裂纹梁；有限单元法；振动；疲劳裂纹扩展

中图分类号:TH113.1 文献标志码:文献标识码:A

文章编号:1672-7207（2020）04-0953-09

Fatigue life predication model for cracked beam structure based on finite element method

LONG　Hui^{1, 2}, LIU　Yilun¹, LI　Songbai¹

(1. School of Mechanical Engineering, Central South University, Changsha 410083, China；

2. School of Physics and Mechanical & Electrical Engineering, Shaoguan University, Shaoguan 512005, China)

Abstract: Based on the coupling analysis of vibration and fatigue crack growth, a method was proposed for fatigue life predication of cracked beam structure. Firstly, dynamic model of a cracked beam structure was established by the finite element method. The stress intensity factor of cracked beam element was derived based on the characteristics of the beam element. Walker’s equation was employed to establish the fatigue crack growth increment. Then, the fatigue crack growth life was obtained through a procedure in which the vibrating response and the crack propagation were simultaneously calculated cyclically. Based on the fatigue life prediction model, the effects of the loading frequency, loading amplitude and stress ratio on the fatigue crack growth were studied. Finally, an experiment study was conducted to validate the proposed model with the comparison between the simulation results and the experimental results. The results show that the proposed model is capable of revealing the internal relationships between the fatigue crack growth and structure parameters and predicting the effects of vibration on the crack growth life. When the loading frequency is near the natural frequencies of the cracked beam, the fatigue life of the cracked beam decreases rapidly with the increase of the crack growth rate. The stress intensity factor range of the cracked beam increases with the increase of the loading amplitude, which leads to the decrease of the fatigue life. The fatigue life is improved significantly when the stress ratio increases.

Key words: cracked beam; finite element method; vibration; fatigue crack growth

梁结构在航空航天、机械、汽车和建筑等领域广泛使用^[1^-2]。大部分梁结构在使用过程中不仅承受动载荷作用，而且受服役环境的影响。由于腐蚀、温度波动和疲劳等多种原因，梁结构中容易产生裂纹。在动载荷作用下，这些裂纹会不断扩展并导致断裂。因此，梁结构的疲劳裂纹扩展问题一直备受关注。为了保证梁结构的安全可靠运行，在梁结构设计中，迫切需要考虑疲劳载荷的影响，准确预测裂纹扩展寿命。近年来，国内外一些学者采用经典解析法研究了裂纹梁的振动疲劳问题。例如，LIU等^[3]将裂纹等效成扭转刚度，建立了裂纹梁横向振动微分方程，研究了摩擦阻尼对疲劳裂纹扩展寿命的影响；马一江等^[4]将裂纹模拟成无质量的弯曲弹簧，建立了含多条裂纹梁的横向振动微分方程，根据边界条件和协调条件推导了应力强度因子表达式，基于Pairs方程，分析了加载频率对裂纹扩展寿命的影响；刘文光等^[5]将裂纹等效成拉伸弹簧和扭转弹簧，建立了裂纹梁的横向振动模型，研究了振动与裂纹扩展耦合关系对疲劳寿命的影响。裂纹梁结构的动力学模型是振动疲劳寿命分析的基础，目前，裂纹梁结构动力学建模方法主要有经典解析法^[3^-6]和有限单元法^[7^-9]。例如，REZAEE等^[6]基于弹性力学建立了裂纹梁的动力学方程，研究了裂纹位置和尺寸对裂纹梁稳态响应的影响；ANDREAUS等^[7]采用有限单元法建立了裂纹梁的运动方程，研究了裂纹闭合效应对裂纹梁动态响应的影响。在经典解析法中，首先建立裂纹梁弹性力学方程，然后，根据边界条件和裂纹处的协调条件求得解析解。但是，由于梁结构的形状和载荷作用方式多样，除了少数比较简单梁结构外，按经典弹性力学方法获得解析解十分困难，甚至不可能^[10]。另外，考虑裂纹扩展影响时，裂纹梁的刚度呈现时变性，裂纹梁动力学方程是非线性的，不可能直接求得其解析解^[7]。为了求得近似解析解，即使是简单的含裂纹悬臂梁弹性力学方程，也需要简化成单自由度模型分析^[5]，局限于分析第1阶模态的影响^[8]。与经典解析法不同，有限单元法能考虑更多的自由度，裂纹梁有限元模型能准确模拟裂纹梁的动态响应^[9]，还能应用于复杂梁结构分析^[11]。此外，有限单元法采用数值方法不仅能直接计算响应，而且能更好地求解非线性方程^[7]。然而，目前，在研究裂纹梁结构振动疲劳时，鲜见采用有限单元法建立裂纹梁结构疲劳寿命预测模型的相关报道。为了建立裂纹梁结构疲劳寿命预测模型，本文作者基于有限单元法建立裂纹梁结构的动力学模型。根据裂纹梁单元的特点，推导裂纹梁单元的应力强度因子表达式，在此基础上应用Walker方程建立疲劳裂纹扩展增量计算式，基于振动响应与裂纹扩展循环同步分析法，计算疲劳裂纹扩展寿命。

1 裂纹梁单元的刚度矩阵

裂纹梁单元模型如图1所示。裂纹梁单元包含2个节点，每个节点包括3个自由度，即轴向位移u，横向位移v和转角θ。相应节点力分量分别为轴向力F、剪力P和弯矩M。裂纹为单边裂纹，在梁的宽度方向扩展一致。为了分析简便又不失普遍性，这里没有考虑裂纹表面接触的影响。基于欧拉伯努利梁假设，忽略剪切变形对裂纹梁的影响，在线弹性范围内，无裂纹梁单元的应变能W₀可表示为^[12]

(1)

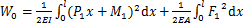
式中：E为弹性模量；I为惯性矩；l为梁单元长度；A为梁的横截面积；F₁，P₁和M₁分别为单元左端节点的轴向力、剪力和弯矩。

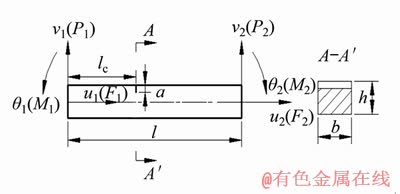
FX_GRP_ID8000210D

图1　裂纹梁单元模型

Fig. 1　Schematic model of cracked beam element

根据线弹性断裂力学，裂纹产生的额外应变能W₁可表示为^[13]

(2)

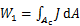
式中：A_c为裂纹面积；J为应变能释放率。

根据Griffith-Irwin理论，应变能释放率J可表示为^[14]

(3)

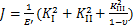
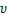
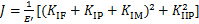
式中：对于平面应力，E＇=E；对于平面应变，E＇=E/(1-ν²)，为泊松比；K_I，K_II和K_III分别为张开型、滑开型和撕裂型裂纹的应力强度因子。根据图1中裂纹梁单元的受载形式，只考虑张开型(I型)和滑开型(II型)断裂的影响，应变能释放率J进一步表示为

(4)

式中：K_IF，K_IP和K_IM分别为纵向力、横向力和弯矩产生的张开型裂纹应力强度因子；K_ⅡP为横向力产生的滑开型裂纹应力强度因子。

(5)

(6)

(7)

(8)

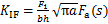
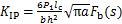
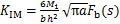
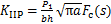
式中：s为裂纹相对深度，s=a/h，a为裂纹深度，h为梁高度；b为裂纹梁宽度；l_c为裂纹位置到单元左端节点的长度。应力强度因子的修正函数F_a(s)，F_b(s)和F_c(s)分别为^[15]

(9)

(10)

(11)

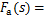
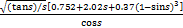
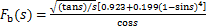
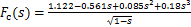
根据卡氏定理，无裂纹梁单元的柔度系数表示为^[15]

(12)

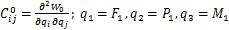
裂纹引起的柔度系数可表示为

(13)

裂纹梁单元的总柔度系数可表示为

(14)

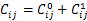
根据图1中裂纹梁单元的节点力，裂纹梁平衡条件表示为

(15)

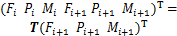
式中：。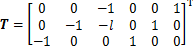

根据虚功原理，裂纹梁单元的刚度矩阵k_c可表示为

(16)

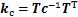
式中：C=C⁰+C¹，C⁰为由无裂纹梁单元的柔度系数组成的矩阵，C¹为由裂纹引起的柔度系数组成的矩阵。由以上推导可知：裂纹梁单元刚度矩阵k_c与裂纹引起的柔度矩阵C¹有关；当C¹=0时，裂纹梁单元刚度矩阵k_c等于无裂纹梁单元的刚度矩阵k_e，即k_c=k_e。

2 裂纹梁结构的振动

根据圣维南原理，裂纹仅影响其附近区域的应力场^[12]。因此，当裂纹梁单元长度大于一定值时，裂纹仅影响其单元内的刚度，对相邻单元刚度的影响可以忽略不计^{[7, 12]}。为了方便分析，忽略裂纹对梁结构质量和阻尼影响，也就是说，裂纹梁单元的质量矩阵m_c等于无裂纹梁单元的质量矩阵m_e，其计算模型见文献[16]。

2.1　裂纹梁结构的运动微分方程

由于工程梁结构形状多样，为便于理解一般裂纹梁结构的建模过程，以图2所示的含裂纹GARTEUR AG-11结构^[17]为例，推导裂纹梁结构的动力学方程。GARTEUR AG-11梁结构划分为n个梁单元，第2个单元为裂纹梁单元，其他为无裂纹梁单元，每个梁单元的节点包括3个自由度。对于任意第i个单元，其运动方程为

(17)

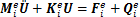
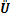
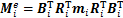
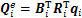
式中：和U分别为整体坐标系下的加速度列阵和坐标列阵；

(18)

(19)

(20)

(21)

B_i为第i个梁单元的协调矩阵；R_i为第i个梁单元的坐标转换矩阵；f_i为作用于第i个梁单元上的外力；q_i为其他梁单元作用于第i梁单元上的单元作用力；m_i为第i个梁单元的质量矩阵；k_i为第i个梁单元的刚度矩阵，当i=2时，k₂= k_c，当i≠2时，k_i= k_e。

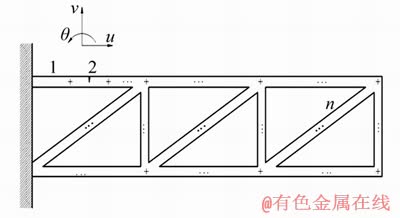
FX_GRP_ID80002FE5

图2　含裂纹GARTEUR AG-11结构的有限元模型

Fig. 2　Finite element model of GARTEUR AG-11 structure with cracks

将含裂纹GARTEUR AG-11结构中的n个梁单元的运动方程叠加，采用黏性阻尼模型^[16]，得到其运动微分方程：

(22)

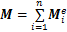
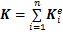
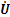
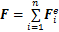
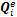
式中：M为裂纹梁结构的整体质量矩阵，；K为裂纹梁结构的整体刚度矩阵，；C为裂纹梁结构的阻尼矩阵；为整体坐标系下的速度列阵；F为外力列阵，。需要注意的是，各单元叠加后，单元间相互作用力抵消。

由以上推导可知：对其他结构形式的裂纹梁结构也可采用以上方法建立其动力学方程，这说明本文建模方法具有普遍性。

2.2　方程的求解

为求得裂纹梁的瞬态响应，采用Newmark法^[16]求解裂纹梁结构动力学方程(22)。选择时间步长△t、参数r和参数β，取r=0.5，β=0.25，△t=1/(20f)，其中，f为激振力的频率。

3 裂纹扩展

由于裂纹尖端具有应力奇异性，裂纹梁结构的最薄弱环节一般在裂纹位置。在裂纹梁结构振动过程中，裂纹梁结构的疲劳寿命往往由疲劳裂纹扩展决定。应力强度因子是预测裂纹扩展寿命中的关键参数。与裂纹试件相比，裂纹梁结构形状和载荷作用方式更复杂，目前还没有统一的应力强度因子计算公式。为了准确计算裂纹梁结构的疲劳寿命，本文利用有限元离散性的特点，将裂纹梁单元作为研究对象，通过裂纹梁单元的应力强度因子预测裂纹梁结构的疲劳寿命。

3.1　裂纹梁单元的名义应力

假设梁中性线在裂纹处连续，采用三次埃尔米特插值多项式，图1中裂纹位置的横向位移v(x)和轴向位移u(x)分别为^[16]

(23)

(24)

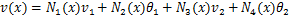
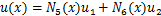
式中：N₁(x)，N₂(x)，N₃(x)，N₄(x)，N₅(x)和N₆(x)为型函数；；；；；；。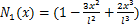

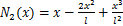
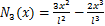
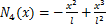
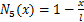
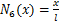
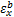
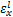
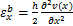
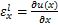
根据材料力学理论，图1中裂纹位置的弯曲应变和拉伸应变分别为

(25)

(26)

根据应力应变关系，裂纹位置处的弯曲名义应力σ₁和拉伸名义应力σ₂分别为

(27)

(28)

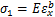
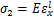
3.2　裂纹梁单元的应力强度因子幅

假定裂纹在扩展过程中沿直线往前扩展。根据裂纹梁单元的应力形式，将弯矩和拉伸引起的应力强度因子叠加，得到裂纹梁单元的应力强度因子K_I表达式：

(29)

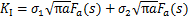
裂纹梁结构在振动过程中，由于名义弯曲应力和名义拉伸应力的变化，应力强度因子也一直处于动态变化中。因此，在1个振动周期内，裂纹梁单元的应力强度因子幅△K_I表示为

(30)

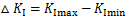
式中：K_Imax和K_Imin分别为1个周期内应力强度因子的最大值和最小值。

3.3　裂纹扩展速率

目前，已有许多关于裂纹扩展速率da/dN与△K_I关系的经验公式。Walker公式考虑了应力比R的影响，对裂纹稳定扩展阶段的适用性较好，是最为广泛应用的公式之一^[18]。Walker公式的表达式如下：

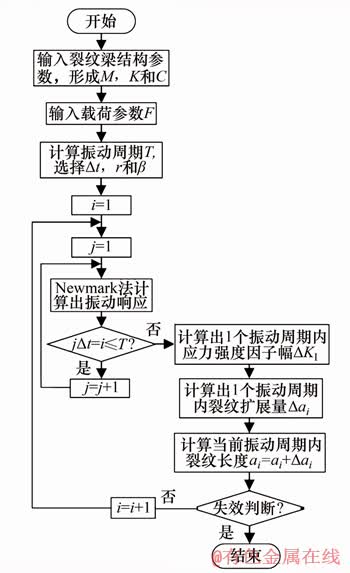
FX_GRP_ID800055CF

图3　裂纹梁结构振动与疲劳耦合分析流程

Fig. 3　Flow chart of couple analysis of fatigue and vibration of cracked beam structure

(31)

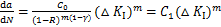
式中：C₀，m和γ为材料常数。

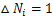
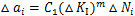
由于应力强度因子幅△K_I动态变化，式(31)不能直接积分得到裂纹扩展增量，必须采用数值积分计算。为了分析简便，取每1个振动周期作裂纹扩展计算，即，则1个振动周期内裂纹扩展增量为

(32)

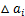
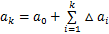
由于裂纹在当前振动周期扩展，裂纹梁结构的刚度K相应改变。为了计算下1个振动周期的裂纹扩展量△a_i+₁，首先需要重新计算裂纹梁结构的振动响应U，然后求出裂纹梁单元的应力强度因子幅△K_I，再根据式(32)求得下1个振动周期的裂纹扩展量△a_i₊₁，通过循环接循环的往复计算，第k次振动周期的裂纹长度a_k为

(33)

式中：a₀为初始裂纹长度。

3.4　裂纹梁结构的失效准则

为了评价裂纹梁结构的疲劳寿命，本文采用失效的准则如下：

1) 最大应力强度因子K_max达到并超过材料断裂韧性K_Ic，即K_max≥K_Ic。

2) 非裂纹截面的应力σ大于等于材料的屈服极限σ_y，即σ≥σ_y。

3) 当裂纹扩展长度a_k到达梁的中性轴时，即a_k≥h/2。

4 裂纹梁结构振动与疲劳耦合分析

图3所示为裂纹梁结构的振动与疲劳耦合计算流程图，步骤如下：

1) 输入裂纹梁结构参数，形成质量矩阵M，刚度矩阵K和阻尼矩阵C。

2) 输入载荷参数F。

3) 计算振动周期T，选择时间步长△t，参数r和β。

4) 采用Newmark迭代法计算1个振动周期内的振幅。

5) 计算1个振动周期内的应力强度因子幅△K_I。

6) 计算1个振动周期内的裂纹扩展量△a_i。

7) 根据失效准则，判断是否达到终止条件。

8) 更新裂纹长度，重复步骤4)~7)，直至裂纹梁结构失效为止。

5 仿真分析

简支梁是常用的梁结构之一。为求简便而不失普遍性，采用图4所示的含裂纹简支梁进行数值计算。简支梁的长度为266 mm，宽和高均为20 mm。裂纹位于简支梁中间，初始裂纹长度为1 mm。简支梁的材料为7075-T651铝合金，其材料参数如表1所示。循环载荷P作用在简支梁的中间，加载的应力比R(R=P_min/P_max，P_max和P_min分别为载荷最大值和最小值)为0.1。为满足计算精度要求且计算简便，简支梁划分为5个梁单元，每个梁单元长度为53.2 mm，其中，裂纹划分在第3个梁单元的中间位置。假定阻尼矩阵能使正则振型对其正交，每个模态的正则振型阻尼比为0.05。首先将简支梁的几何参数、材料参数和边界条件代入式(17)~(22)，然后根据频率方程公式^[16]，得到含裂纹简支梁的第1阶固有频率f₁为684 Hz。

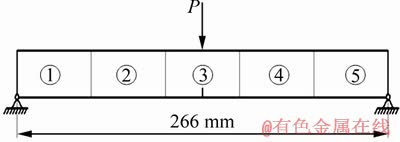
FX_GRP_ID80000A08

图4　含裂纹简支梁的仿真模型

Fig. 4　Simulation model of simple supported beam with crack

表1　7075-T651铝合金的材料参数

Table 1　Material data of 7075-T651 aluminum alloy

5.1　载荷频率对裂纹梁疲劳寿命的影响

当最大载荷力P_max为3 kN，应力比R为0.1时，不同载荷频率下简支梁振动循环次数N与裂纹扩展长度a的曲线如图5(a)所示。由图5(a)可见：在相同最大载荷和应力比下，随着激振频率f从10 Hz增大到539 Hz，裂纹长度从1 mm扩展到8 mm的循环次数降低。以f为10 Hz的循环次数为基准，当f为337 Hz时振动循环次数降低46%，当f为539 Hz时振动循环次数降低85%；随着激振频率接近固有频率，含裂纹简支梁的振幅越来越大，裂纹梁单元应力强度因子幅△K_I增大，疲劳裂纹扩展速率增加，疲劳裂纹扩展寿命降低。

5.2　载荷幅值对裂纹梁疲劳寿命的影响

当应力比R为0.1，加载频率f为10 Hz时，不同载荷下简支梁振动循环次数N与裂纹扩展长度a的曲线如图5(b)所示。由图5(b)可见：在相同应力比和频率下，随着激振力从3 kN增大到5 kN，裂纹长度从1 mm扩展到8 mm的循环次数降低；随着激振力增大，裂纹位置处的振动幅值增大，裂纹梁单元的应力强度因子幅△K_I增大，疲劳裂纹扩展速率增加，疲劳裂纹扩展寿命降低。

5.3　应力比对裂纹梁疲劳寿命的影响

当最大载荷力P_max为3 kN，加载频率f为10 Hz时，不同应力比下简支梁振动循环次数N与裂纹扩展长度a的曲线如图5(c)所示。由图5(c)可见：在相同的最大载荷力和频率下，随应力比R从0增加到0.5，裂纹长度从1 mm扩展到8 mm的循环次数增加。在此需要说明的是，当R＜0时，一般认为压应力部分对裂纹扩展速率没有影响^[18]，也就是说，在相同的最大载荷力下，认为应力比R＜0和R=0具有相同的疲劳裂纹扩展寿命。以应力比R为0的循环次数为基准，R为0.1时振动循环次数增加15%，R为 0.3时振动循环次数增加62%，R为0.5时振动循环次数增加155%。随着应力比R增大，应力强度因子的最小值K_Imin增大，而应力强度因子的最大值K_Imax保持不变。因此，应力强度因子幅△K_I降低，疲劳裂纹扩展速率降低，裂纹梁的振动循环次数得到大幅度提升。

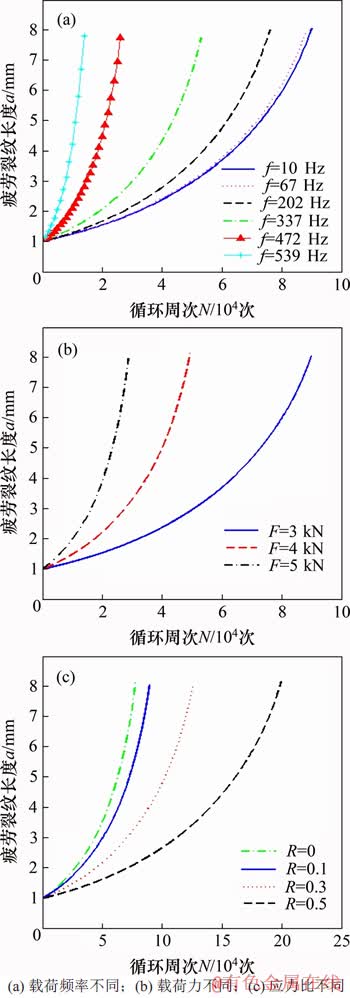
FX_GRP_ID800041AA

图5　载荷对裂纹扩展寿命的影响

Fig. 5　Effect of load on fatigue crack growth

6 试验验证

6.1　7075-T651材料的裂纹扩展试验

试验材料为上海航铝航空材料有限公司提供的7075-T651铝合金，板厚度为4 mm。材料屈服强度为523 MPa，弹性模量E为71.7 GPa。根据文献[19]，采用标准紧凑拉伸试样开展材料的裂纹扩展试验。试件尺寸如图6(a)所示。在室温条件下，在MTS810疲劳试验机上进行疲劳裂纹扩展试验。试验施加正弦波恒幅载荷，最大载荷力P_max为1.2 kN，应力比R为0.1，加载频率f为20 Hz。

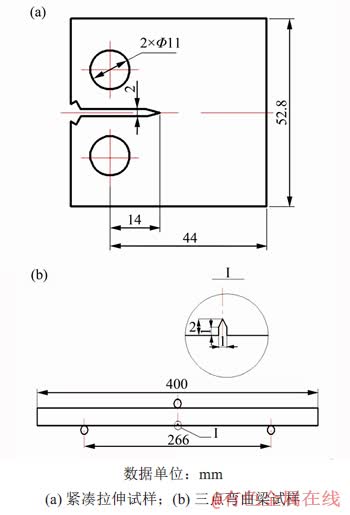
FX_GRP_ID800017F3

图6　试样尺寸

Fig. 6　Dimensions of test samples

6.2　裂纹梁的三点弯曲疲劳试验

为了验证模型的准确性，采用7075-T651铝合金梁进行三点弯曲疲劳试验。梁试件的尺寸如图6(b)所示，长、宽和高分别为400，20和20 mm。为了预制疲劳裂纹，试件上切割出1个V形槽。搭建的三点弯曲疲劳试验装置包括伺服疲劳试验机(SDS200)、三点弯曲夹具和工业检测视频显微镜(AOSVI AF216C)。为了通过显微镜准确测量疲劳裂纹长度，试样的表面用砂纸抛光处理。裂纹梁通过三点弯曲夹具固定在疲劳试验机上，两端的跨距为266 mm，载荷作用在梁的中间位置。

采用恒幅载荷预制疲劳裂纹，预制出裂纹长度分别为3.153 mm和3.063 mm这2组试件，分别称为试件1和试件2。试件1的最大载荷力P_max为3 kN，应力比R为0.1，加载频率f为10 Hz。试件2的最大载荷力P_max为4 kN，应力比R为0.1，加载频率f为10 Hz。两者的最大载荷不同，其他载荷一致。

6.3　试验结果

采用对数坐标处理原始试验数据，紧凑拉伸试件应力强度因子幅△K与裂纹扩展速率da/dN的关系如图7所示。取图7中△K从10 MPa·m^1/2到23 MPa·m^1/2稳定裂纹扩展区数据，进行采用线性拟合，拟合结果如图8所示，得到应力比R为0.1时，材料裂纹稳态扩展常数C₁为2.205 5×10^-7，m为2.116。

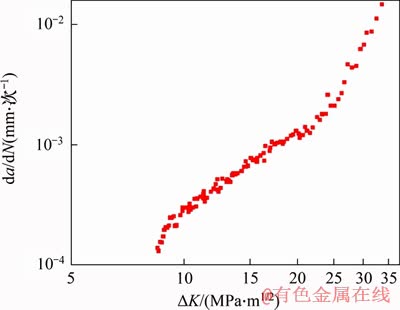
FX_GRP_ID8000446F

图7　紧凑拉伸试样在R=0.1时da/dN与△K的曲线

Fig. 7　Relationship between da/dN and △K of compact tension specimen at R=0.1

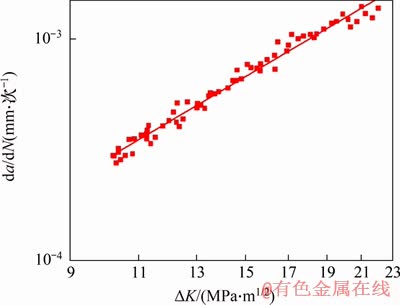
FX_GRP_ID800045D2

图8　裂纹扩展速率在R=0.1时的拟合结果

Fig. 8　Fitting results of crack growth rate at stress ratio R=0.1

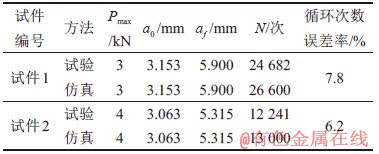
三点弯曲疲劳试验结果如表2所示。从表2可见：试件1从裂纹长度3.153 mm扩展至裂纹长度5.900 mm的循环次数为24 682次。试件2从裂纹长度3.063 mm扩展至裂纹长度5.315 mm的循环次数为12 241次。

6.4　数值分析与试验结果比较

为了验证本文模型的准确性，将本文理论计算的裂纹扩展次数与试验结果对比。由于试验过程中P_min>0，裂纹梁在受迫振动过程中始终处于受压状态，在支点处相当于无纵向位移，因此，将图6(b)中的试验结构简化为图4中的有限元模型，数值计算的疲劳裂纹扩展结果如表2所示，其中，试件1的振动循环次数为26 600次，试件2的振动循环次数为13 000次。从表2可见：试件1和试件2的循环次数预测误差分别为7.8%和6.2%。从对比结果看，仿真和试验循环次数的最大误差不超过8.0%，循环次数预测结果与试验结果基本一致，验证了本文提出模型的正确性。

表2　三点弯曲梁的仿真结果与试验结果对比

Table 2　Numerical and experimental results of three-point bending tests

7 结论

1) 基于裂纹梁结构的有限元模型，推导得到裂纹梁结构在疲劳载荷作用下的裂纹扩展表达式，建立了裂纹梁结构疲劳寿命预测模型。

2) 通过对2根裂纹梁的试验研究和数值计算，仿真和试验的循环次数最大误差不超过8.0%，裂纹扩展次数的预测结果与试验结果基本一致，验证了本文提出模型的准确性。

3) 随着激振频率接近固有频率，疲劳裂纹扩展速率增大，裂纹梁的疲劳寿命降低明显；随着激振力幅值增大，裂纹梁的应力强度因子幅增大，疲劳裂纹扩展寿命降低；随着应力比增加，裂纹梁的疲劳寿命显著提高。

参考文献：

[1] 卫军, 杜永潇. 基于固有频率的梁结构疲劳损伤演化规律[J]. 中南大学学报(自然科学版), 2019, 50(8): 1866-1875.

WEI Jun, DU Yongxiao. Fatigue damage evolution of Timoshenko beams based on natural frequency[J]. Journal of Central South University(Science and Technology), 2019, 50(8): 1866-1875.

[2] LONG Hui, LIU Yilun, HUANG Changzheng, et al. Modelling a cracked beam structure using the finite element displacement method[J]. Shock and Vibration, 2019, 2019: 1-13.

[3] LIU Wenguang, BARKEY M E. The effects of breathing behaviour on crack growth of a vibrating beam[J]. Shock and Vibration, 2018, 2018: 1-12.

[4] 马一江, 陈国平. 含多条裂纹梁的模态与振动疲劳寿命分析[J]. 振动、测试与诊断, 2017, 37(2): 307-313, 405.

MA Yijiang, CHEN Guoping. Analysis of mode and vibration fatigue life of beam with multiple cracks[J]. Journal of Vibration, Measurement & Diagnosis, 2017, 37(2): 307-313, 405.

[5] 刘文光, 陈国平. 含裂纹悬臂梁的振动与疲劳耦合分析[J]. 振动与冲击, 2011, 30(5): 140-144.

LIU Wenguang, CHEN Guoping. Coupling analysis for vibration and fatigue of a cracked cantilever beam[J]. Journal of Vibration and Shock, 2011, 30(5): 140-144.

[6] REZAEE M, SHATERIAN-ALGHALANDIS V. A new crack detection method in a beam under geometrically nonlinear vibration[J]. Archive of Applied Mechanics, 2018, 88(9): 1491-1506.

[7] ANDREAUS U, BARAGATTI P. Cracked beam identification by numerically analysing the nonlinear behaviour of the harmonically forced response[J]. Journal of Sound and Vibration, 2011, 330(4): 721-742.

[8] BOUBOULAS A S, ANIFANTIS N K. Finite element modeling of a vibrating beam with a breathing crack: observations on crack detection[J]. Structural Health Monitoring: An International Journal, 2010, 10(2): 131-145.

[9] BOVSUNOVSKY A, SURACE C. Non-linearities in the vibrations of elastic structures with a closing crack: A state of the art review[J]. Mechanical Systems and Signal Processing, 2015, 62/63: 129-148.

[10] 李世芸, 肖正明. 弹性力学及有限元[M]. 北京: 机械工业出版, 2016: 1-7.

LI Shiyun, XIAO Zhengming. Elastic mechanics and finite element method[M]. Beijing: China Machine Press, 2016: 1-7.

[11] LIN R M, NG T Y. Applications of higher-order frequency response functions to the detection and damage assessment of general structural systems with breathing cracks[J]. International Journal of Mechanical Sciences, 2018, 148: 652-666.

[12] MUSCOLINO G, SANTORO R. Dynamics of multiple cracked prismatic beams with uncertain-but-bounded depths under deterministic and stochastic loads[J]. Journal of Sound and Vibration, 2019, 443: 717-731.

[13] EL YAAGOUBI M , JUHRE D, MEIER J, et al. Prediction of energy release rate in crack opening mode (mode I) for filled and unfilled elastomers using the Ogden model[J]. Engineering Fracture Mechanics, 2017, 182: 74-85.

[14] EROGLU U, TUFEKCI E. Exact solution based finite element formulation of cracked beams for crack detection[J]. International Journal of Solids and Structures, 2016, 96: 240-253.

[15] HOU Chuanchuan, LU Yong. Identification of cracks in thick beams with a cracked beam element model[J]. Journal of Sound and Vibration, 2016, 385: 104-124.

[16] 辛格雷苏S R. 机械振动[M]. 李欣业, 杨理诚, 译. 北京: 清华大学出版社, 2016: 435, 455, 728-730.

SINGIRESU S R. Mechanical vibrations[M]. LI Xinye, YANG Licheng, trans. Beijing: Tsinghua University Press, 2016: 435, 455, 728-730.

[17] OHAYON R. GARTEUR TP-095 final report: finite element updating of structural vibrations using numerical experimental simulation[R]. Amsterdam: GARTEUR Structures and Materials Action Group, 1997: 1-24.

[18] DOWLING N E, STEPHEN L K, MILO V K. Mechanical behavior of materials[M]. 5th ed. London: Pearson Prentice Hall, 2019: 509-533.

[19] GB/T 6398—2000. 金属材料疲劳裂纹扩展速率试验方法[S].

GB/T 6398—2000. Standard test method for fatigue crack growth rates of metallic materials[S].

（编辑秦明阳）

收稿日期： 2019 -09 -02; 修回日期： 2019 -11 -08

基金项目(Foundation item)：国家自然科学基金资助项目 (51375500; 51575358) (Projects(51375500; 51575358) supported by the National Natural Science Foundation of China)

通信作者：刘义伦，博士，教授，从事工程构件疲劳寿命预测理论与方法研究；E-mail：liuyiluncsu@sina.com

摘要:为了准确预测裂纹梁结构的疲劳寿命，提出一种裂纹梁结构的振动与疲劳裂纹扩展耦合分析方法。首先，基于有限单元法建立裂纹梁结构的动力学模型；然后，根据裂纹梁单元的特点，推导裂纹梁单元的应力强度因子表达式，在此基础上应用Walker方程建立疲劳裂纹扩展增量计算式，再基于振动响应与裂纹扩展循环同步分析法，计算疲劳裂纹扩展寿命；基于该疲劳寿命预测模型，分析激振频率、激振力幅值和应力比对裂纹梁疲劳寿命的影响；最后，对裂纹梁进行疲劳试验，将试验测量结果与模型计算结果进行比较，验证所提出模型的准确性。研究结果表明：提出的疲劳寿命预测模型较好地表征了疲劳裂纹扩展寿命与其结构参数之间的内在关系，反映了振动对裂纹梁结构疲劳寿命的影响；随着激振频率接近固有频率，裂纹扩展速率增大，裂纹梁的疲劳寿命明显降低；随着激振力幅值增大，裂纹梁的应力强度因子幅增大，疲劳裂纹扩展寿命降低；随着应力比增加，裂纹梁的疲劳寿命显著提高。