Hydrogen desorption kinetics mechanism of Mg-Ni hydride under isothermal and non-isothermal conditions

Chao-yi CHEN¹, Hui-lin CHEN², Ya-qin MA², Jing LIU²

1. College of Materials and Metallurgy, Guizhou University, Guiyang 550003, China;

2. School of Materials and Architectural Engineering, Guizhou Normal University, Guiyang 550001, China

Received 12 January 2015; accepted 13 May 2015

Abstract:

The Mg-Ni hydride was prepared by hydriding combustion synthesis under a high magnetic field. The dehydriding kinetics of the hydrides was measured under the isothermal and non-isothermal conditions. A model was applied to analyzing the kinetics behavior of Mg-Ni hydride. The calculation results show that the theoretical value and the experimental data can reach a good agreement, especially in the case of non-isothermal dehydriding. The rate-controlling step is the diffusion of hydrogen atoms in the solid solution. The sample prepared under magnetic field of 6 T under the isothermal condition can reach the best performance. The similar tendency was observed under the non-isothermal condition and the reason was discussed.

Key words:

Mg-Ni hydride; hydrogen desorption kinetics; model; isothermal condition; non-isothermal condition;

1 Introduction

As a hydrogen storage alloy, Mg₂Ni intermetallic is well known to form Mg₂NiH₄ hydride, which has hydrogen storage capacity of 3.6% (mass fraction). The absorption/desorption kinetics of this hydride is a reversible formation/decomposition reaction which can be described as α-Mg₂NiH_0.3+H₂β-Mg₂NiH₄. The kinetics mechanism of Mg-Ni alloy has been studied and many kinetics models and functions have been established [1-3]. However, as far as most of kinetics equations are concerned, if one treats each step rigorously, a group of differential or integral equations must be solved [4,5]. Some treatments are so complicated that they cannot offer an explicit analytic expression and give an intuitionally quantitative discussion. Owing to the lack of parameter values, the other situation is that some equations are often difficult to be applied.

As we know, most of the hydrogen absorption/ desorption kinetics data were obtained under isothermal condition [6,7]. Actually, it is very difficult to achieve isothermal condition completely since the reaction is highly exothermic for hydrogenation and endothermic for dehydrogenation and the rate is fast for both processes. Therefore, even if correct kinetic models are chosed, the calculation results should still deviate from the experimental curves since the practical reaction deviates from the isothermal condition. Recently, the non-isothermal hydrogen absorption/desorption kinetics of Mg-Ni intermetallic was investigated using DSC, TG or Sievert’s method [8-11]. However, the theoretical investigation on non-isothermal absorption/desorption kinetics in Mg₂Ni intermetallic obviously lags behind the experiments. There are still many problems that have not been theoretically solved yet, such as, what kind of curve should be expected regarding the reacted fraction versus temperature in a non-isothermal process, and what is the effect of heating rate on the kinetics, and how to calculate the activation energy through the non-isothermal kinetic experimental data.

The present work firstly synthesized Mg-Ni hydride by hydriding combustion synthesis under a high magnetic field. Then, a kinetics model proposed by our group [12,13] was applied to analyzing the dehydriding kinetics mechanism of Mg-Ni hydride under both isothermal and non-isothermal cases. The influence of preparation and hydrogen desorption conditions on the kinetics behavior was investigated.

2 Experimental

Elemental powders of Mg with 99.5 % in purity and ~170 μm in particle size, Ni with 99.9% in purity and 2-3 μm in particle size were well mixed by an agate pestle to yield Mg₂Ni stoichiometric mixed powders. The handling of the sample was always carried out under argon in a glove box. Then, the mixed powders were put in an autoclave. Before experiment, the autoclave was repeatedly evacuated and filled in H₂ with pressure of 0.5 MPa three times. Then, the autoclave was put in the central part of furnace and filled with H₂ with pressure of 4.0 MPa. A high magnetic field was applied in the center of samples [14,15]. Finally, the samples were heated up to 673 K to make the Mg and Ni mixtures react with hydrogen for 4 h. The samples prepared without magnetic field, under magnetic fields of 4, 6 and 8 T were labeled as S₀, S₄, S₆ and S₈, respectively.

The isothermal dehydriding kinetics was measured at 553, 573 and 623 K under 0.001 MPa of H₂. The non-isothermal dehydriding kinetics was measured by heating the samples from room temperature to 650 K under 0.001 MPa of H₂ at different heating rates, and the amount of hydrogen absorbed as a function of temperature derived from the recorded data of temperature and pressure. Both isothermal and non-isothermal dehydriding kinetics were measured by a Sieverts-type PCT characteristics measurement system (PCT–2SDWIN, Suzuki Shokan Co., Ltd.). Then, the kinetics data were analyzed by model to study the dehydriding behavior.

The phase compositions of the samples were carried out by X-ray diffraction (XRD) (Panalytical X'pert PRO) using monochromatic Cu K_α radiation.

Before starting the dehydriding kinetics experiments, the Mg-Ni composites were cyclic activated under 4 MPa of H₂ at 623 K until the absorption volume was stabilized. Figure 1 shows the XRD patterns of samples after hydriding/dehydriding cycles. The relative content of Mg₂NiH₄ after being treated under magnetic fields of 0, 4, 6 and 8 T were calculated as 64.42%, 84.34%, 93.07% and 68.29%, respectively.

3 Models

The dehydriding process is a kind of complicated heterogeneous reaction and the mathematic treatment should be very complicated and it is hard to obtain a simple solution. The purpose of this work is stressed on the kinetics model which can express the relation between the reacted fraction and time (isothermal) or temperature (non-isothermal) and calculate the corresponding parameters under reasonable simplified assumptions. Moreover, these formulae can be used to analyze the kinetic mechanism.

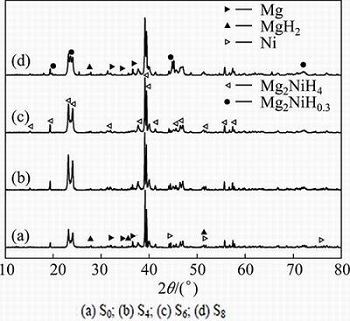
Fig. 1 XRD patterns of samples after hydriding/dehydriding cycles activation: (a) S₀; (b) S₄; (c) S₆; (d) S₈

The model assumes that all particles of the hydrogen storage alloy or its hydride could be regarded as spherical balls with the same density and radius (R₀). The diffusion of hydrogen atoms in the solid solution will be the rate controlling step for the hydrogen absorption/desorption processes. A set of formulae deduced under the rate controlling step of diffusion were introduced to describe the dehydriding of Mg-Ni hydride.

3.1 Calculation formulae of particle dehydriding under isothermal condition

The relation of the dehydriding reacted fraction ξ and time t can be expressed as [12]

(1)

where E_v is the activation energy (J/mol), R is the mole gas constant, T is the thermodynamic temperature (K), B_t is a coefficient which can be expressed as

(2)

where and are the constants independent of temperature but relying on the material, υ_m represents the constant coefficient that depends on the density of storage material, is the hydrogen partial pressure in equilibrium with hydride, is the initial pressure, and R₀ is the radius of particle. If the particle radius and temperature are fixed, there is a relation between B_t and E_v which can be expressed as

(3)

where T₀ is the dehydriding reaction temperature, t_c is the characteristic reaction time of the hydriding reaction corresponding to T₀ and can be expressed as

(4)

where represents the diffusion coefficient of hydrogen in the solid solution, represents the equilibrium composition of hydrogen in hydride as the dehydriding reaction reaches equilibrium and is the concentration of hydrogen atoms in the solid solution phase just underneath the particle surface at radius R₀.

Equation (1) describes the reacted fraction (ξ) of dehydriding under isothermal condition as an explicit function of time (t), temperature (T) and particle size (R₀). The advantage of Eq. (1) is that the explicit analytic solution can be found easily. Otherwise, Eqs. (1)-(4) reveal the physical meaning of parameter “k” that appears in both JANDER’s [16] and CARTER’s [17] formulae. The parameter “k” in these formulae was expressed as a function of temperature T and hydrogen concentration C and its reciprocal is t_c, as describe in Eqs. (3) and (4), which is the characteristic reaction time and has the physical meaning of the required time for the particle to be completely dehydrogenated. The smaller the t_c, the faster the dehydriding reaction rate. This indicates that the isothermal dehydriding kinetics performance of hydrogen storage materials can be quantified with accuracy using the characteristic reaction time directly. The isothermal kinetics model has been successfully applied to several hydrogen storage materials including La₂Mg₁₇-based composite [18], LaNi₅ intermetallic [19], Zr-based AB₂ alloys [20] and Mg-based composite [21].

3.2 Calculation formulae of particle dehydriding under non-isothermal condition

On the other hand, for many other dehydriding processes, their service temperature is not constant but variable, for example, at an elevated temperature. When the furnace is heated, the temperature rises with a certain heating rate. If the system is heated from the temperature T₀, the relation of temperature with time t should be

(5)

where η = dT/dt is the heating rate and the relation of the reacted fraction ξ with temperature T can be expressed as [17]

(6)

where T_i is the initial reaction temperature.

Equation (6) can be used to describe the relation of the reacted fraction of dehydriding with temperature when the temperature changes at a certain rate η. It can be seen that higher increase rate of temperature will correspond to lower reacted fraction ξ. In addition, for a hydrogen storage system, the reacted fraction ξ=Ф corresponding to a certain T_Ф with a fixed heating rate. T_Ф is defined as the characteristic reaction temperature (Ф usually is 0.5, 0.875 or 1), which is a very important and useful parameter and its physical meaning is the temperature for the particle to be dehydrogenated to a certain extent (ξ=Ф) at a certain heating rate. T_Ф relates to the property of hydrogen storage material, heating rate, hydrogen partial pressure and particle size. The smaller the T_Ф, the faster the dehydriding reaction rate. This indicates that the non-isothermal dehydriding kinetics performance of hydrogen storage materials can be quantified using the characteristic reaction temperature directly. The non-isothermal kinetics model has also been successfully applied to the oxidation kinetics of zirconium carbide [22] and multi-walled carbon nanotubes [23].

In this study, the dehydriding kinetics of Mg₂NiH₄ was measured under the isothermal and non-isothermal conditions. The model mentioned above was applied to analyzing the kinetics behavior. The characteristic reaction time t_c, characteristic reaction temperature T_Ф and activation energy E_v were attained by non-linear fitting directly. The calculated results were compared with the measurements and the validity of proposed model and rate equations were discussed.

4 Results and discussion

4.1 Dehydriding kinetics under isothermal condition

The reacted fraction ξ was used to describe the dehydriding kinetic of alloy. The relation between the reacted fraction ξ and the fraction of reacted amount is

(7)

where Δm is the reacted amount, m₀ is the initial amount of the sample,Δm/m₀ is the fraction of reacted amount and Δm_max represents the maximum reacted amount.

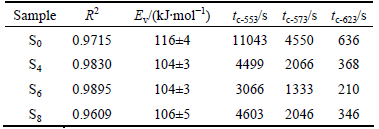
Figure 2 shows the isothermal dehydriding curves under 0.001 MPa of H₂ and different temperatures for the Mg₂NiH₄. In order to achieve a quantitative analysis and clarify the mechanism, the experimental data of dehydriding were fitted by Eq. (1) using non-linear fitting. The results are listed in Table 1 and a series of fitted curves are also shown in Fig. 2. It can be seen that the corresponding R² of non-linear regression equations are 0.9715, 0.9830, 0.9895 and 0.9609 for S₀, S₄, S₆ and S₈, respectively. Therefore, the experimental data and the theoretical calculated results reach an acceptable agreement which indicates that the dehydriding processes are controlled by the diffusion of hydrogen atoms in the solid solution from 553 to 623 K.

Fig. 2 Isothermal dehydriding curves together with fitted curves under 0.001 MPa of H₂ and different temperatures: (a) S₀; (b) S₄; (c) S₆; (d) S₈

Moreover, from non-linear fitting results, the parameters E_v can be evaluated by using Eq. (1) and the results are listed in Table 1. It can be seen that the activation energies of desorption for S₀, S₄, S₆ and S₈ are ~116, ~104, ~104 and ~106 kJ/mol, respectively. From E_v and Eq. (3), t_c at different temperatures can be calculated, where t_c-553, t_c-573 and t_c-623 are t_c at 553, 573 and 623 K, respectively. It is found that the minimum t_c comes from S₆. Combining with the results of E_v, it can be concluded that the optimum treated magnetic field is 6 T. The isothermal dehydriding kinetics of S₆ is nearly three times faster than that of S₀. The phenomena may results from the phase compositions of the samples. It can be seen from Fig. 1(a) that S₀ has a multiphase structure, composed of Mg₂NiH₄, MgH₂, Mg as well as Ni. With an increase of magnetic intensity (6 T), as shown in Fig. 1(c), most of the major peaks belong to Mg₂NiH₄, coexisting with trace of Mg₂NiH_0.3. For S₈, another multiphase structure, which is composed of Mg₂NiH₄, Mg₂NiH_0.3, MgH₂ and Mg, can be observed, as shown in Fig. 1(d). During the dehydriding process, unreacted Mg or MgH₂ may act as the diffusion barrier to decrease the hydrogen atoms diffusion coefficient. On the other hand, the dehydriding kinetics of MgH₂ is inferior to that of Mg₂NiH₄.

Table 1 Fitting results of isothermal dehydriding for Mg₂NiH₄

4.2 Dehydriding kinetics under non-isothermal condition

Figure 3 shows the non-isothermal dehydriding curves of Mg₂NiH₄ under 0.001 MPa of H₂ corresponding to the heating rates of 2, 5 and 10 K/min. It can be seen that sigmoid experimental data points, which have similar tendency, are obtained for all the samples. S₄ is taken as an example to illustrate the tendency: the dehydriding begins at about 460 K and reaches the maximum at about 550 K when the heating rate is 5 K/min, and the temperature corresponding to the maximal dehydriding rate increases from about 540 to 575 K with the heating rate increasing from 2 to 10 K/min.

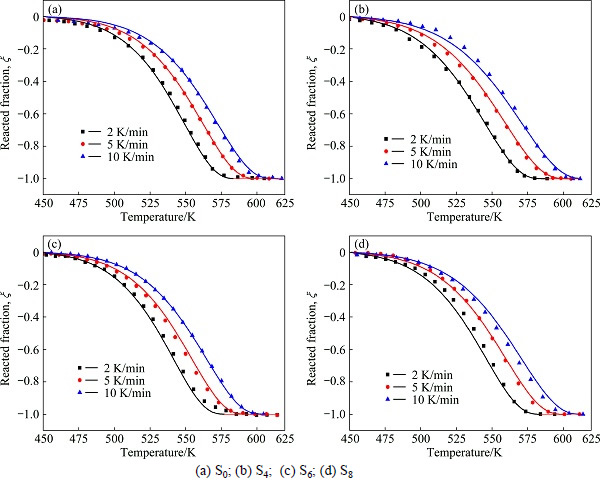
Fig. 3 Non-isothermal dehydriding curves together with fitted curves under 0.001 MPa of H₂ and different heating rates

However, these data cannot be quantitatively compared without the model analysis. Therefore, Eq. (6) was used to fit the non-isothermal kinetics data with non-linear fitting method. The corresponding parameters were calculated and are listed in Table 2. A series of fitted curves are also shown in Fig. 3. From Table 2, it can be seen that the corresponding R² of non-linear regression equations are 0.9980, 0.9986, 0.9959 and 0.9980 for S₀, S₄, S₆ and S₈, respectively. Therefore, the experimental data and the theoretical calculated results reach an excellent agreement which indicates that the

Table 2 Fitting results of non-isothermal dehydriding for Mg₂NiH₄

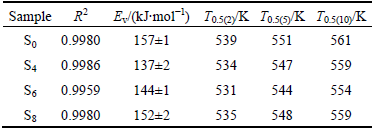
non-isothermal dehydriding processes are controlled by the diffusion of hydrogen atoms in the solid solution with the heating rate increasing from 2 to 10 K/min.

Moreover, from the non-linear fitting results, the parameters E_v can be evaluated using Eq. (6) and the results are listed in Table 2. It can be seen that the activation energies of non-isothermal dehydriding for S₀, S₄, S₆ and S₈ are ~157, ~137, ~144 and ~152 kJ/mol, respectively. The activation energies under non-isothermal condition have similar tendency but are all higher than those under isothermal condition. The possible interpretation is that for a heating process, the energy enhances with the increase of temperature and the dehydriding cannot react until the requirements of thermodynamics and dynamics can be satisfied simultaneously. The manifestation form of dynamics condition is the activation energy barrier or superheat. On the other hand, for most of isothermal dehydriding processes, the initial energy is high enough to overcome the activation energy barrier and the reaction occurs instantaneously. As we know, the activation energy barrier is much higher than the reaction energy. Therefore, the activation energy under non-isothermal condition is higher than that under isothermal condition.

Moreover, from Eq.(6), T_0.5 under different heating rates were calculated and are listed in Table 2, where T_0.5(2), T_0.5(5) and T_0.5(10) are T_Ф=0.5 under the heating rates of 2, 5 and 10 K/min, respectively. The non-isothermal dehydriding rates can be compared using characteristic reaction temperature directly. The minimum T_0.5 comes from S₆ for non-isothermal dehydriding. This conclusion is similar to that of the isothermal dehydriding.

After comparing the fitting results, it may be seen that the corresponding R² of non-linear regression equations for non-isothermal dehydriding are all higher than those for isothermal dehydriding, which indicates that the errors for the former are smaller than those for the latter. As mentioned above, it is very difficult to achieve isothermal condition accurately in the dehydriding process of Mg₂NiH₄ since the reaction is highly endothermic for dehydrogenation and the initial rate is fast. Figure 4 shows the actual temperatures of the dehydriding processes for S₆ under the isothermal(573 K) and non-isothermal (5 K/min) conditions. It can be seen that the actual temperature of the isothermal dehydriding process is deviated from the isothermal conditions, especially in the initial stage. Moreover, some experiment conditions, such as particle size, in different experiments are not exactly identical. Plus the approximation of assumption, there should be some other errors between the experimental data and theoretical calculation. However, as long as the assumption is reasonable and the introduced error is tolerant, this kind of approximate treatment should be acceptable.

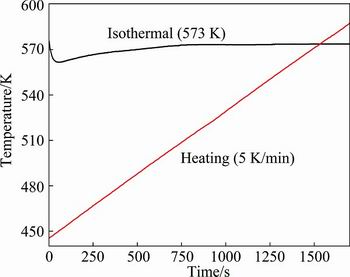
Fig. 4 Actual temperatures of dehydriding processes for S₆ under isothermal and non-isothermal conditions

It can be seen that the theoretical model can give a reasonable prediction no matter what kind of experimental condition is set, isothermal or non-isothermal. In the above derivation of formulae, the premise of deduction is assumed that the diffusion of hydrogen atoms in the solid solution is the controlling step. The successful application to Mg₂NiH₄ demonstrates that this assumption is acceptable in the dehydriding processes. For some general case, the controlling step may vary in a whole dehydriding process; however, the controlling step for hydrogen diffusion in the solid solution will still occupy a large part of time, especially in the later time of reaction. Therefore, this model can be applied successfully in many cases.

5 Conclusions

1) The Mg-Ni hydride was prepared by hydriding combustion synthesis under a high magnetic field. The dehydriding kinetics of the hydride was measured under the isothermal and non-isothermal conditions and analyzed by model. In the derivation of the model, two new conceptions, characteristic reaction time and characteristic reaction temperature, are introduced. This model can be used to analyse. The isothermal and non-isothermal dehydriding kinetics gives a quantification result.

2) The calculated results show that the theoretical calculation and the experimental data can reach a good agreement, especially in the case of non-isothermal dehydriding. Under the isothermal condition, the rate-controlling step is the diffusion of hydrogen atoms in the solid solution. The sample prepared under magnetic field of 6 T can reach the best performance. The dehydriding kinetics under the non-isothermal condition has a similar tendency but the activation energies are all higher than those of isothermal condition. The kinetics analysis results of non-isothermal dehydriding are more accurate than those of isothermal dehydriding.

References

[1] AKIBA E, NOMURA K, ONO S, SUDA S. Kinetics of the reaction between Mg-Ni alloys and H₂ [J]. Int J Hydrogen Energy, 1982, 7(11): 787-791.

[2] OUYANG L Z, CAO Z J, WANG H, LIU J W, SUN D L, ZHANG Q A, ZHU M. Dual-tuning effect of In on the thermodynamic and kinetic properties of Mg₂Ni dehydrogenation [J]. Int J Hydrogen Energy, 2013, 38(21): 8881-8887.

[3] CHERNOV I, BLOCH J, VOIT A, GABIS I. Influence of metal powder particle’s shape on the kinetics of hydriding [J]. Int J Hydrogen Energy, 2010, 35(1): 253-258.

[4] MILANESE C, GIRELLA A, BRUNI G, COFRANCESCO P, BERBENNI V, MATTEAZZI P, MARINI A. Mg–Ni–Cu mixtures for hydrogen storage: A kinetic study [J]. Intermetallics, 2010, 18(2): 203-211.

[5] ZHANG Yang-huan, SONG Chun-hong, REN Hui-ping, LI Zhi-gang, HU Feng, ZHAO Dong-liang. Enhanced hydrogen storage kinetics of nanocrystalline and amorphous Mg₂Ni-type alloy by substituting Ni with Co [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(9): 2002-2009.

[6] LUO Q, AN X H, PAN Y B, ZHANG X, ZHANG J Y, LI Q. The hydriding kinetics of Mg-Ni based hydrogen storage alloys: A comparative study on Chou model and Jander model [J]. Int J Hydrogen Energy, 2010, 35(15): 7842-7849.

[7] LI Q, CHOU K C, LIN Q, JIANG L J, ZHAN F. Influence of the initial hydrogen pressure on the hydriding kinetics of the Mg_2-xAl_xNi (x=0; 0.1) alloys [J]. Int J Hydrogen Energy, 2004, 29(13): 1383-1388.

[8] ZHOU H Y, LAN X X, WANG Z M, YAO Q R, NI C Y, LIU W P. Effect of rapid solidification on phase structure and hydrogen storage properties of Mg₇₀(Ni_0.75La_0.25)₃₀ alloy [J]. Int J Hydrogen Energy, 2012, 37(17): 13178-13184.

[9] LASS E A. Hydrogen storage in rapidly solidified and crystallized Mg-Ni-(Y,La)-Pd alloys [J]. Int J Hydrogen Energy, 2012, 37(12): 9716-9721.

[10] LIU X F, ZHU Y F, LI L Q. Hydrogen storage properties of Mg_100-xNi_x (x=5, 11.3, 20, 25) composites prepared by hydriding combustion synthesis followed by mechanical milling (HCS+MM) [J]. Intermetallics, 2007, 15(12): 1582-1588.

[11] SINGH R K, SADHASIVAM T, SHEEJA G I, SINGH P, SRIVASTAVA O N. Effect of different sized CeO₂ nano particles on decomposition and hydrogen absorption kinetics of magnesium hydride [J]. Int J Hydrogen Energy, 2013, 38(14): 6221-6225.

[12] CHOU K C, XU K D. A new model for hydriding and dehydriding reaction in intermetallics [J]. Intermetallics, 2007, 15(5): 767-777.

[13] ZHOU Guo-zhi, LI Qian. Thermodynamics and kinetics of magnesium- based hydrogen storage material [J]. Chinese Journal of Nature, 2011, 33(1): 6-12. (in Chinese)

[14] LI Q, LIU J, CHOU K C, LIN G W, XU K D. Synthesis and dehydrogenation behavior of Mg–Fe–H system prepared under an external magnetic field [J]. J Alloy Compd, 2008, 466(1-2): 146-152.

[15] LIU J, LI Q, CHOU K C. Mg-Ni-H hydrogen storage system prepared by controlled hydriding combustion synthesis [J]. Advanced Materials Research, 2011, 197-198: 749-752.

[16] JANDER W. Reactions in solid state at high temperatures [J]. Z Anorg Allg Chem, 1927, 163(1): 1-30.

[17] CARTER R E. Kinetic model for solid-state reactions [J]. J Chem Phys, 1961, 34(6): 2010-2015.

[18] LIU Jing, LI Qian. Hydriding/dehydriding behaviors of La₂Mg₁₇– 10wt% Ni composite prepared by mechanical milled [J]. Journal of Rare Earths, 2013, 31(1): 73-78.

[19] AN X H, LI L G, ZHANG J Y, LI Q. Comparison of dehydriding kinetics between pure LaNi₅ and its substituted systems [J]. J Alloy Compd, 2012, 511(1): 154-158.

[20] CUI X Y, LI Q, CHOU K C, CHEN S L, LIN G W, XU K D. A comparative study on the hydriding kinetics of Zr-based AB₂ hydrogen storage alloys [J]. Intermetallics, 2008, 16(5): 662-667.

[21] PAN Y B, WU Y F, LI Q. Modeling and analyzing the hydriding kinetics of Mg-LaNi₅ composites by Chou model [J]. Int J Hydrogen Energy, 2011, 36(20): 12892-12901.

[22] HOU X M, CHOU K C. Investigation of the effects of temperature and oxygen partial pressure on oxidation of zirconium carbide using different kinetics models [J]. J Alloy Compd, 2011, 509(5): 2395-2400.

[23] SINGH A K, HOU X M, CHOU K C. The oxidation kinetics of multi-walled carbon nanotubes [J]. Corrosion Science, 2010, 52(5): 1771-1776.

Mg-Ni氢化物等温及非等温放氢动力学机理

陈朝轶¹，陈辉林²，马亚芹²，刘 静²

1. 贵州大学 材料与冶金学院，贵阳 550003；

2. 贵州师范大学 材料与建筑工程学院，贵阳 550001

摘  要：利用强磁场下的氢化燃烧合成技术制备Mg-Ni氢化物。在等温和非等温条件下测试该氢化物的放氢动力学性能。利用一个新模型分析Mg-Ni氢化物的放氢动力学机理。结果显示，理论计算结果与实验数据吻合良好，尤其是在非等温条件下。Mg-Ni氢化物体系在放氢过程的控制步骤是氢原子在基体中的扩散。在6 T强磁场下合成的氢化物样品在等温和非等温条件下都具有最佳的放氢综合性能，并对其原因进行分析。

关键词：Mg-Ni氢化物；放氢动力学；模型；等温；非等温

(Edited by Mu-lan QIN)

Foundation item: Project (51464008) supported by the National Natural Science Foundation of China; Project (KY[2012]004) supported by the Key Laboratory Item of Education Office in Guizhou Province, China

Corresponding author: Jing LIU; Tel: +86-851-83227440; E-mail: liujing_lynn@126.com

DOI: 10.1016/S1003-6326(16)64101-8

Abstract: The Mg-Ni hydride was prepared by hydriding combustion synthesis under a high magnetic field. The dehydriding kinetics of the hydrides was measured under the isothermal and non-isothermal conditions. A model was applied to analyzing the kinetics behavior of Mg-Ni hydride. The calculation results show that the theoretical value and the experimental data can reach a good agreement, especially in the case of non-isothermal dehydriding. The rate-controlling step is the diffusion of hydrogen atoms in the solid solution. The sample prepared under magnetic field of 6 T under the isothermal condition can reach the best performance. The similar tendency was observed under the non-isothermal condition and the reason was discussed.