
J. Cent. South Univ. (2020) 27: 3090-3102
DOI: https://doi.org/10.1007/s11771-020-4531-7
A-BQ, a classification system for anisotropic rock mass based on China National Standard
GUO Song-feng(郭松峰)1, 2, 3, QI Sheng-wen(祁生文)1, 2, 3, SAROGLOU Charalampos1, 4
1. Key Laboratory of Shale Gas and Geoengineering, Institute of Geology and Geophysics,Chinese Academy of Sciences, Beijing 100029, China;
2. Innovation Academy of Earth Science, Chinese Academy of Sciences, Beijing 100029, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. School of Civil Engineering, National Technical University of Athens, Athens, Greece
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract:
The rock mass in nature is in most cases anisotropic, while the existing classifications are mostly developed with the assumption of isotropic conditions that not always meet the engineering requirements. In this study, an anisotropic system based on China National Standard of BQ, named as A-BQ, is developed to address the classification of anisotropic rock mass incorporating the anisotropy degree as well as the quality of rock mass. Two series of basic rating factors are incorporated including inherent anisotropy and structure anisotropy. The anisotropy degree of rock mass is characterized by the ratio of maximum to minimum quality score and adjusted by the confining stress. The quality score of rock mass is determined by the key factors of anisotropic structure occurrence and the correction factors of stress state and groundwater condition. The quality of rock mass is characterized by a quality score and classified in five grades. The assessment of stability status and probable failure modes are also suggested for tunnel and slope engineering for different quality grades. Finally, two cases of tunnel and slope are presented to illustrate the application of the developed classification system into the rock masses under varied stress state.
Key words:
anisotropy; rock mass; basic quality; classification; tunnel; slope;
Cite this article as:
GUO Song-feng, QI Sheng-wen, SAROGLOU Charalampos. A-BQ, a classification system for anisotropic rock mass based on China National Standard [J]. Journal of Central South University, 2020, 27(10): 3090-3102.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-020-4531-71 Introduction
As valuable and acceptable tools for engineers, a number of rock mass classification systems have been developed for the past decades starting from TERGAZHI [1]. Nowadays, the classification approach serves as indispensable basis during the design and construction of complex excavations in rock masses. The rock mass classification system should incorporate three factors generally. Firstly, the properties of rock matrix, e.g., strength and deformation of intact rocks, make a basic contribution to the ratings. Secondly, the features of rock mass structure, e.g., the density, orientation and surface condition of discontinuities, play a dominant role on the rock mass quality. Finally, the geological circumstances of rock masses, e.g., geostress and ground water, should also be considered to correct the final ratings. Besides, the systems should be reliable and easy to use in practice. Therefore, among these proposed classification methods, only a few have worldwide rock mass engineering and design, such as RMR [2], Q [3], RMi [4], GSI [5].
Besides the worldwide notable classification systems mentioned above, some countries also developed their own systems to support the engineering constructions. China has conducted a large number of rock mass engineerings in the past decades including hydropower stations, railways, highways, mines, etc. The first rock mass quality classification that should be noted was Z system developed in 1970s [6]. Following that the basic quality (BQ) classification system that was issued originally in 1994 and updated in 2014 is the only mandatory national standard [7, 8]. The BQ involves two basic factors and three corrected factors. The basic factors include rock integrity coefficient and rock hardness coefficient, which reflects the effects of discontinuities and rock strength respectively. The three corrected factors are initial geostress, ground water and discontinuity orientation, which mainly reflect the correction of geological environment as well as geometric relation between the rock engineering and large discontinuities.
As stated by BARTON et al [9], anisotropy is everywhere while isotropy is rare. Despite some trials have been performed to anisotropic rock mass using the above-mentioned classification systems [10, 11], and some systems do take into account the effects of large weak discontinuities, e.g., RMR and BQ, the effective classification for anisotropic rock mass is still far from being well solved. A recent progress is the ARMR that proposed by SAROGLOU et al [12] for the rating of anisotropic rock masses similar to RMR rating system. ARMR considered six basic parameters, i.e., anisotropic strength index, uniaxial compressive strength of intact rock; degree of structure anisotropy, corrected RQD, condition of anisotropy surfaces (bedding, schistosity or joints) and groundwater conditions. The effects of confining stress on the anisotropic degree are also considered to adjust the final rating. In ARMR, the rock mass anisotropy degree is an important factor to evaluate rock mass quality and usually rock masses with high anisotropy degree have low quality. Nevertheless, as stated by HUDSON et al [13], the anisotropy variation of rock mass could be gradual within the intact rock or sudden as a discontinuity is crossed. It indicates that the rock mass anisotropy is more complex resulting from the discontinuities and should be elaborated further.
In this study, a classification system for anisotropic rock masses based on BQ, denoted as A-BQ, is proposed. In the second section, the overall approach to present the classification system is introduced briefly. In the third section, the rating approach for anisotropy degree and quality of anisotropic rock masses involving the anisotropic structure orientation is presented respectively. Besides, the corresponding stability assessment for rock mass in slope and tunnel engineering is also suggested in this section. In the fourth section, some cases of anisotropic rock mass are studied to illustrate the application of the presented A-BQ classification system. In the fifth section, a brief concluding remark is presented.
2 Approach to propose classification system
An anisotropic rock mass has different properties in different directions. Therefore, the anisotropic degree and quality of rock mass should be distinguished distinctly when being classified. The former one denotes the variation degree of properties in different directions, which is always classified by the ratio of highest parameters to lowest parameters for anisotropic intact rock, e.g., uniaxial strength [14], ultrasonic velocity [15], point load strength [16], deformation modulus and Poisson ratio [17, 18], longitudinal wave velocity index [19] as well as the tensile strength [20].
On the other hand, the quality of anisotropic rock mass should be predicted considering the orientation of the anisotropic structure for a certain rock mass. The quality may be better for a rock mass with higher anisotropy degree when the orientation of anisotropic structure falls in some range. For example, as shown in Figure 1, the anisotropy degree of rock mass A is higher than B. However, A has higher strength when the orientation of anisotropic structure is smaller than β1 and bigger than β2, but has lower strength when the orientation of anisotropic structure is between β1 and β2.
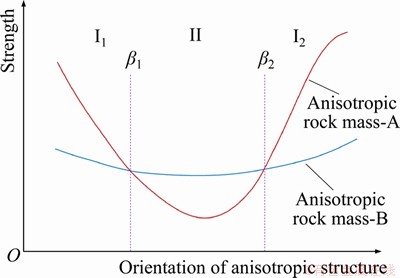
Figure 1 Strength anisotropy for two types of anisotropic rock masses
Consequently, the classification system for anisotropic rock masses should incorporate the ratings of anisotropy degree and rock mass quality considering anisotropic structure orientation, both of which are incorporated in the proposed classification system.
The classification system is put forward on the basis of China National Standard-basic quality (BQ). The BQ were originally presented through statistical analysis of 103 typical rock mass engineering from various industries in 1994 and modified in 2014. Over 25 years of extensive applications in China and some other countries, the BQ has been validated as a reliable classification system. Thus, most of the equations and classification thresholds in the developed classification system follow those in BQ. The anisotropy degree of anisotropic rock mass, which is not incorporated in the BQ, is classified based on the data analysis in the existing publications.
3 A-BQ classification system
3.1 Rating for anisotropy degree
The behavior of anisotropic rock mass is basically dependent on the inherent strength anisotropy of rock matrix and structure anisotropy resulting from discontinuities [12, 21]. As described in the previous section, the original BQ system considered both the rock strength and integrity of rock mass. In the presented A-BQ system, the rock strength anisotropy as well as the structure anisotropy is incorporated.
3.1.1 Inherent strength anisotropy of rock matrix
According to SAROGLOU et al [12], the inherent anisotropy stems from the existence of bedding, foliation and schistosity planes in intact rock. BAGHERIPOUR et al [22] summarized that the anisotropic intact rocks mainly incorporate foliated metamorphic rocks and stratified sedimentary rocks. The former rock types such as schist, slates, gneisses and phyllite always contain a natural orientation in their flat/long minerals or a banding phenomenon (Figure 2(a)). The latter rock types such as sandstone, shale, mudstone often display anisotropic behaviour due to the presence of bedding planes (Figure 2(b)). Besides, it should be mentioned that some igneous rocks can also be highly anisotropic due to eruption sequences and flow structures, e.g. basaltic rocks and rhyolites [23].

Figure 2 Anisotropic rock masses in multi scale:
The mechanical behavior anisotropy of such rocks has been studied extensively since 1960s. To depict the strength anisotropy, researchers have developed a number of methods mostly based on the existing theories or criterions originally for isotropic materials, e.g., Mohr-Coulomb criterion [24, 25], Griffith theory [26, 27] or Hoek-Brown criterion [28, 29]. Besides, some other equations are also determined based on experiments empirically [30-33]. As mentioned above, the inherent anisotropy of rocks has also been classified on the basis of properties anisotropy [14,16-19].
The saturated uniaxial compressive strength (Rc) is adopted as the strength parameter in the original BQ. Similarly, the maximum and the minimum saturated uniaxial compressive strength should be applied in the presented A-BQ system, which are denoted by Rcmax and Rcmin, respectively. Rcmax can be determined by uniaxial compression tests with loading perpendicular to the anisotropic plane of saturated rock, while Rcmin can be determined by uniaxial compression tests when loading direction has an angle (usually between 25° and 45°) with the anisotropic plane.
If it is difficult to conduct the uniaxial compression tests, the point load strength index of specimen with a diameter equal to 50 mm Is(50) can be adopted to determine the Rc. Some equations have been developed to depict the relation between Is(50) and rock strength [34-36]. Here the equation developed on the basis of back analysis from a large amount of representative rocks is recommended, which is developed by Research Institute of Railway Construction in China [8]. Rcmax and Rcmin should be estimated by Eqs. (1) and (2) respectively.
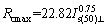 (1)
(1)
 (2)
(2)
where  and
and are Is(50) under loading perpendicular and parallel, respectively, to the foliation planes at the axial and diametral test [19].
are Is(50) under loading perpendicular and parallel, respectively, to the foliation planes at the axial and diametral test [19].
Rc is determined from a uniaxial compression test on saturated intact rock samples through different loading directions with anisotropic plane. When no experimental data of Rc is available, but the uniaxial compressive strength in dry conditions is known, Eq. (3) proposed by VASARHELYI [37] can be used to determine Rc.
Rc=0.759σc-dry (3)
3.1.2 Structure anisotropy of rock mass
The structural anisotropy is characterized by presence of bedding or schistosity in rock masses with engineering scale (Figure 2(c)). The degree of discontinuity development in rock mass is determined by the rock mass integrity index Kv. The rock mass integrity has been calibrated by a variety of parameters including joint spacing, RQD, volumetric joint count (Jv), the number of joint sets (Jn), joint length (JL) and block volume (Vb), etc.
In A-BQ, the maximum and minimum Kv should be determined by the following equations preferably:
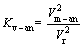 (4)
(4)
 (5)
(5)
where Kv-an denotes the integrity index stemming from the anisotropic structures and Kv-ra denotes the integrity index due to other discontinuities excluding anisotropic structures. Vr denotes the longitudinal wave velocity of intact rock, while Vm-an and Vm-ra denote the longitudinal wave velocity of rock mass. Vr should be determined through ultrasonic tests on core samples in which wave propagation is parallel to the inherent anisotropy of intact rocks. Vm-an can be generally determined through in situ velocity measurement perpendicular to the anisotropy structures, while Vm-ra can be determined through in situ velocity measurement parallel to the anisotropy structures of rock mass.
The rock mass integrity can be classified as five classes according to Kv, i.e., integrated for Kv of 0.75-1, moderately integrated for Kv of 0.55- 0.75, slightly fragmented for Kv of 0.35-0.55, moderately fragmented for Kv of 0.15-0.35 and highly fragmented for Kv of 0-0.15 (Table 1). The spacing of anisotropic planes was also considered to estimate the integrity [12].
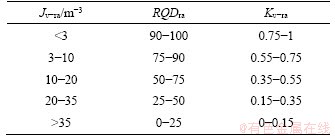
In this study, the spacing of anisotropic structures can also be adopted to determine Kv-an roughly if it is difficult to conduct the in situ velocity measurement in the field, the classification values of which is referred to those in Ref. [12] (Table 1). The RQD stemming from the anisotropic structures (RQDan) can also be considered and the classification approach is referred to Ref. [38]. The RQDan should be used with caution and calculated in drill cores in a scan-line perpendicular to the anisotropic structures in order to account for the anisotropy dependence. For the discontinuities excluding anisotropic structures, the corrected RQD (RQDra) that exclude the anisotropic structures can also be adopted to determine Kv-ra (Table 2). Besides, the volumetric joint count number (Jv-ra) that exclude the anisotropic structures is also recommended to determine the rock mass integrity which is referred to the BQ [8] (Table 2).
Table 1 Determination of rock mass integrity index Kv-an stemming from anisotropic structure (modified from Ref. [8, 12])
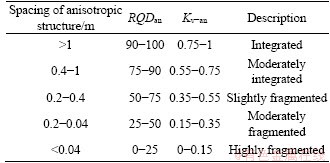
Table 2 Determination of rock mass integrity index Kv-ra stemming from discontinuities excluding anisotropic structures (modified from Ref. [8])
To limit the effects of very high strength of rock mass with intensively developed discontinuities, the following restrictions should be complied [8].
When Rcmax>90Kv-ra+30,
Rcmax=90Kv-ra+30 (6)
When Rcmin>90Kv-an+30,
Rcmin=90Kv-an+30 (7)
On the other hand, to limit the effects of sparsely developed discontinuities for rock mass with low strength, the following restrictions should be complied.
When Kv-ra>0.04Rcmax+0.4,
Kv-ra=0.04Rcmax+0.4 (8)
When Kv-an>0.04Rcmin+0.4,
Kv-an=0.04Rcmin+0.4 (9)
3.1.3 Classification of anisotropy degree
Based on back analysis of extensive rock mass engineering projects in China in the past decades, an equation is developed for the classification of rock masses [8]. Referred to this equation, the maximum and minimum ratings of ABQ involving direction of anisotropic structure are determined by Eqs. (10) and (11) respectively.
ABQmax=100+3Rcmax+250Kv-ra (10)
ABQmin=100+3Rcmin+250Kv-an (11)
The index of anisotropy degree IBQan should be determined by the ratio of maximum ABQ to minimum ABQ (Eq. 12).
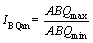 (12)
(12)
The anisotropy degree of rock masses is classified to five grades according to IBQan depicted as massive or isotropic, slightly anisotropic, moderately anisotropic, highly anisotropic and very highly anisotropic respectively (Table 3). Referred to the anisotropy classification of anisotropic rocks [19], the threshold values of different grades are determined through numerous trial studies covering nearly all the range of the rock strength and discontinuity developing conditions. It has been widely recognized that the confining stress has obvious effects on the anisotropy degree [32, 39-44]. As suggested by SAROGLOU et al [12], the classification of anisotropy degree should incorporate the correction of confining stress. According to SAROGLOU [45], in anisotropic rocks the degree of anisotropy decreases with increase of confining stress. The adjustment of confining stress, expressed as σ3/σc, on the final ratings of anisotropy degree are shown in Table 4.
Table 3 Anisotropic degree classification according to IBQan
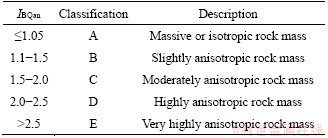
Table 4 Adjustment of confining stress

3.2 Quality classification for anisotropic rock mass in engineering
To classify the quality of anisotropic rock mass, the occurrence of anisotropic structures should be involved in engineering practice. The thresholds of the intersection angle β between anisotropic structure and maximum principal stress (σ1) can be roughly determined by the weak plane theory [24].According to the weak plane theory, the rock mass has the lowest strength when β=45°-φj/2, where φj denotes the friction angle of weak plane. The friction angle is dependent on the discontinuity condition such as interlayer material or roughness, and falls in the range of 20°-40° in general. Accordingly, the rock mass with anisotropy structure of β=25°-35° has the weakest quality. Therefore, the rock mass has the lowest strength when the intersection angle β between anisotropic structure and maximum principal stress (σ1) is 25°-35°, while it has the highest strength when the anisotropic structure is nearly parallel or perpendicular to σ1 (β=0-10° and 70-90°). Consequently, as the curve of strength variation with orientation of anisotropic structure has a U-shape, the score of anisotropic rock mass quality can be roughly determined under this generalized stress state, i.e., ABQ=ABQmax for β=0-10° and 70-90°, ABQ=ABQmin for β=25-45°, and ABQ= for other conditions.
for other conditions.
Accordingly, the classification methods of anisotropic rock mass in tunnel and slope engineering are presented in the following sections.
3.2.1 Tunnel engineering anisotropic rock mass
For the anisotropic rock mass in tunnel engineering, two parameters are incorporated to determine the rock mass quality (ABQt). The first one is the intersection angle between the strike direction of anisotropic structure and the tunnel axis (α1) and the other one is the dip of anisotropic structure (γ1). The ABQt should be scored as ABQmax under the most favorable condition, i.e., α1≥60° and γ1≥75°, as ABQmin under the most unfavorable condition, i.e., α1≤30° and 30°≤γ1≤60°, and as 1/2(ABQmax+ABQmin) under other conditions.
The groundwater affects the rock mass quality and should be considered to correct the final scores. Referred to the original BQ system [8], the groundwater condition is rated as completely dry, damp/wet, dripping, flowing, and quantitatively divided by hydraulic pressure and outflow rate. The rock mass of lower quality is more prone to become weaker when groundwater is present. Therefore, the correction factor is higher for lower original ABQ score. The correction factor of groundwater for tunnel engineering rock mass (Kwt) is shown in Table 5.
In addition to groundwater, geostress is another significant environmental factor that affects the rock mass stability when being excavated. The initial geostress is characterized by the ratio of maximum saturated uniaxial compressive strength of the anisotropic rock mass (Rcmax) to the maximum principal stress in field (σ1). According to BQ system [8], initial geostress state is classified to three levels, i.e., low or intermediate geostress with Rcmax/σ1≥7, high geostress with 4≤Rcmax/σ1<7 and extremely high geostress with Rcmax/σ1<4. No correction is needed for ABQ score under low or intermediate geostress. On the other hand,meticulous corrections should be put forward for rock mass with varied initial ABQ score under high and extremely high geostress, which can be indexed in Table 6.
Table 5 Correction factor of groundwater for tunnel engineering rock mass (Kwt) [8]
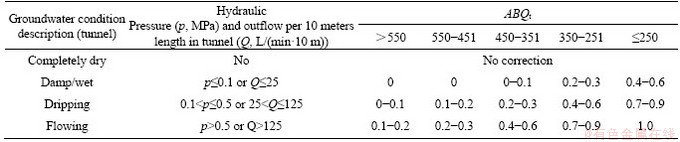
Table 6 Correction factor of initial geostress (Ks)
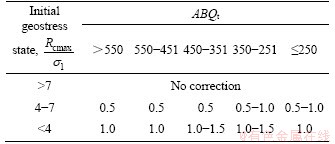
With two correction factors of Kwt and Ks, the corrected quality scores [ABQ]t for the anisotropic rock mass in tunnel engineering should be determined by Eq. (13).
[ABQ]t=ABQt-100×(Kwt+Ks) (13)
3.2.2 Slope engineering anisotropic rock mass
Similarly, the intersection angle between strike direction of anisotropic structure and slope (α2), the dip angle of anisotropic structure (γ2) and the slope dip angle (γs) are adopted to determine the quality of anisotropic rock mass in slope engineering denoted ABQs. The ABQs should be scored as ABQmax under the most favorable condition, i.e., α2≥30°, γ2≤20° and γ2>γs, as ABQmin under the most unfavorable condition, i.e., α2≤10°, γ2≥35° and γ2<γs, and as 1/2(ABQmax+ABQmin) under other conditions.
The quality score of anisotropic rock mass in slope engineering should be corrected by groundwater condition. The groundwater condition is rated as completely dry, damp or dripping, streamline flowing and flashy flowing, and quantitatively divided by hydraulic head. Generally, the rock mass of lower quality is more sensitive to groundwater, which results in higher correction factor. The correction factor of groundwater for slope engineering rock mass (Kws) is shown in Table 7.
With the correction factor of Kws, the corrected quality scores [ABQ]s for the anisotropic rock mass in slope engineering should be determined by Eq. (14).
[ABQ]s=ABQs-100×Kws (14)
3.2.3 Quality classification
The anisotropic rock mass quality is classified to five grades according to the corrected quality scores [ABQ]t and [ABQ]s (Table 8) [8]. The quality of the rock mass reduces from Grade I to Grade V.
3.3 Stability assessment of anisotropic rock mass in engineering
After presenting the classification of anisotropic rock mass in the previous section, the stability assessment of tunnels or slopes is recommended in this section. The suggested stability assessment is developed empirically based on large amount of rock engineering projects in China.
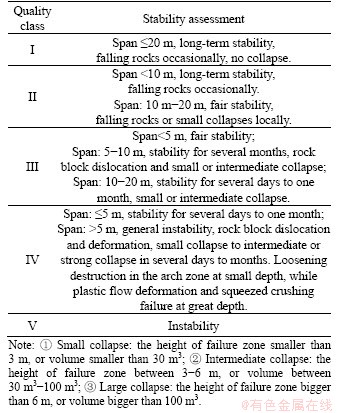
3.3.1 Stability assessment of tunnel engineering
When adopting the suggested stability assessment for tunnel engineering, the span of the tunnel should be smaller than 20 m. The stability status, stand-up time and the most likely failure modes are presented for varied grades of rock mass quality (Table 9) [8].
3.3.2 Stability assessment of slope engineering
When adopting the suggested stability assessment for slope engineering in this study, the slope height should be lower than 60 m. The stability status, stand-up time and the most likely failure modes are presented for varied grades of rock mass quality (Table 10) [8].
4 Application to case studies
In order to illustrate and explain the reliability and practicability of the developed ABQ system, two case studies are presented in this section.
Table 7 Correction factor of ground water for slope engineering rock mass (Kws) [8]
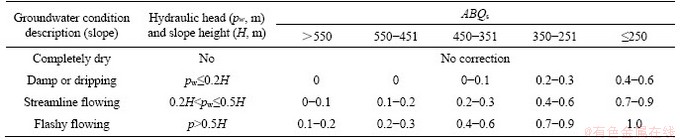
Table 8 Quality classification of anisotropic rock mass engineering [8]
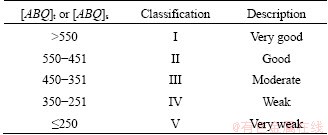
Table 9 Stability assessment of tunnel engineering anisotropic rock mass [8]
4.1 Phyllite rock mass tunnel engineering
A case of layered phyllite rock mass in tunnel engineering was presented by SHA et al [46], which is Liangshui tunnel of Lanzhou-Chongqing railway located in Gansu Province. The phyllite rock mass has a highly anisotropic structure as presented in Figure 3.
4.1.1 Anisotropy degree classification of phyllite rock mass
The steps to reach anisotropy degree of the phyllite rock mass and the results are presented in Table 11.
The results show that Ian of the phyllite rock mass in Liangshui tunnel is about 2.68, which indicate that the anisotropy degree can be classified as E (very highly anisotropic rock mass) initially.
Table 10 Stability assessment of slope engineering anisotropic rock mass [8]


Figure 3 Stratified phyllite rock mass in Liangshui tunnel engineering [46]
According to the measured minimum principal stress in field, the anisotropy degree is adjusted as D (highly anisotropic rock mass) eventually.
4.1.2 Quality classification for Liangshui tunnel engineering
The rock mass quality of tunnel engineering is rated according to the occurrence of anisotropic structure, and then corrected by factors including groundwater condition and initial stress state. The corrected score is then adopted to classify the rock mass quality. The results are shown in Table 12.
The stability status of Liangshui tunnel can be assessed according to Table 9, which indicates that the tunnel is unstable as it is characterized as grade V. As reported, large deformation occurred around the tunnel section after excavation, and even continued for a long period after the installation of the primary support. It is obvious that the prediction is in accordance with what was encountered during tunnel construction.
Table 11 Anisotropic degree rating of phyllite rock mass in Liangshui tunnel
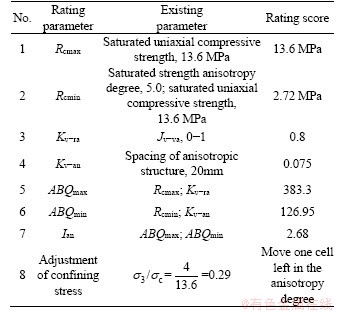
Table 12 Rock mass quality rating of Liangshui tunnel engineering

If BQ classification system is adopted, the corrected BQ score is 209.55, which also falls in grade V but has a much higher score compared with ABQ. In the BQ, no guidance is suggested to determine Rc of anisotropic rocks (here saturated uniaxial compressive strength with loading direction perpendicular to the anisotropic structure is used), and the weight of weak planes is too small as just one of correction factors. Last but not least, the anisotropy degree of the rock mass cannot be obtained in BQ system, which can give an overall estimation of the anisotropic rock mass characteristics for engineers.
4.2 Slate rock mass slope engineering
The slope of a quarry that is located in Jiujiang China was reported by CHEN et al [47] and SAROGLOU et al [12]. The slate has a well- developed slaty structure that was widely encountered in this site (Figure 4).

Figure 4 Slate rock mass of Jiujiang quarry slope
4.2.1 Anisotropy degree classification of slate rock mass
Through similar procedures with that was presented in the classification of the phyllite rock mass, the rating results are presented in Table 13. It is obvious that the anisotropic degree IBQan of the slate rock mass in Jiujiang quarry slope is about 1.876, which indicates that the anisotropy degree can be classified as C (moderately anisotropic rock mass). The classification should not be adjusted for the relatively low confining stress.
4.2.2 Quality classification for Jiujiang quarry slope engineering
After similar procedures of the quality classification tunnel engineering, the results of quality classification can be reached as shown in Table 1. It is shown that the quality score is about 326.84. The quality of Jiujiang quarry slope is classified as grade IV (weak) according to Table 14. The slope height is about 8-15 m, which indicates that it will remain stable for several days to one month and the wedge or toppling failure are the preferable failure modes.
Table 13 Anisotropic degree rating of slate rock mass for Jiujiang quarry slope engineering
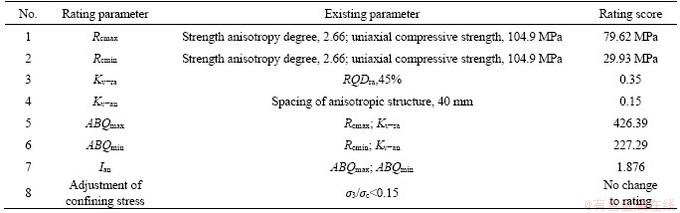
Table 14 Rock mass quality rating of Jiujiang quarry slope engineering

5 Concluding remarks
In this study, the A-BQ system is developed as an extension of BQ system (GB 50218-2014) in order to classify anisotropic rock masses. The A-BQ system classifies the anisotropic rock mass by incorporating the anisotropy degree as well as the quality of rock mass. The maximum and minimum saturated uniaxial compressive strength are adopted to characterize the inherent anisotropy, and the integrity index stemming from the anisotropic structure and other discontinuities are adopted to characterize the structure anisotropy respectively. The restrictive conditions are presented to limit the effects of extreme cases of rock strength and discontinuities. Furthermore, an equation containing saturated compressive strength and integrity index is adopted to determine maximum and minimum quality score of rock mass resulting from anisotropy.
The anisotropy degree of rock mass is characterized by the ratio of maximum to minimum quality score (IBQan) and classified in five grades, i.e., massive or isotropic rock mass, slightly anisotropic, moderately anisotropic, highly anisotropic and very highly anisotropic rock mass. The confining stress is taken into account to adjust the eventual classification of anisotropy degree. The quality of rock mass is determined by the anisotropic structure and correction factors. The procedures to evaluate the quality of slope and tunnel engineering are clarified respectively. The quality of rock mass is characterized by quality score and classified in five grades, i.e., very good, good, moderate, weak and very weak. The assessment of stability status and probable failure modes are also suggested for tunnel and slope engineering in various quality grades. Finally, two case studies are presented to illustrate the application of the developed classification system.
In the system, rock mass anisotropy degree and rock mass quality are distinguished clearly. The basic, key and corrected factors are incorporated, which cover most of the factors in the existing classification systems, i.e., basic factors are the strength of intact rocks and rock mass integrity index, the key factor is the anisotropic structure occurrence and correction factors are the stress state and the groundwater condition.
It should be pointed out that it is preferable to use the wave velocity ratio rather than the volumetric joint count, joint spacing or RQD in order to determine the rock mass integrity. The former index is comprehensive while the latter indices just indicate the density of discontinuities, which means that characteristics such as the type and surface conditions are absent. In addition, the anisotropic structure is considered as one group, and all the other discontinuities are classed as the other group. This simplification may result in underestimation of the anisotropy degree and conservative evaluation of the rock mass quality to a certain extent. The three different quality scores according to the anisotropic structure occurrence may also result in some errors, which is acceptable for the early stage of assessment.
Contributors
GUO Song-feng prepared and revised the manuscript. QI Sheng-wen presented the idea. QI Sheng-wen and SAROGLOU Charalampos conducted revisions.
Conflict of interest
GUO Song-feng, QI Sheng-wen, and SAROGLOU Charalampos declare that they have no conflict of interest.
References
[1] TERZAGHI K. Rock defects and load on tunnel supports [C]// Introduction to Rock Tunneling with Steel Support. Commercial Shearing and Stamping Co., Youngstown, Ohio, 1946: 17-99. https://www.researchgate.net/publication/3740 7995_Rock_Defects_and_loads_on_Tunnel_Supports.
[2] BIENIAWSKI Z. Engineering classification of jointed rock masses [J]. Civil Engineer in South Africa, 1973, 15(12): 335-343. https://journals.co.za/content/civeng/15/12/AJA10 212019_1739.
[3] BARTON N, LIEN R, LUNDE J. Engineering classification of rock masses for the design of tunnel support [J]. Rock mechanics, 1974, 6(4): 189-236. DOI: 10.1007/ BF01239496.
[4] PALMSTROM A. Characterizing rock masses by the RMi for use in practical rock engineering: Part 1: The development of the Rock Mass index (RMi) [J]. Tunnelling and Underground Space Technology, 1996, 11(2): 175-188. DOI: 10.1016/0886-7798(96)00 015-6.
[5] HOEK E, KAISER P K, BAWDEN W F. Support of underground excavations in hard rock [M]. Rotterdam: Balkema, 1995.
[6] GU De-zhen, HUANG Ding-cheng. Classification of rock mass structure and determination of its quality coefficient [J]. Hydrogeology & Engineering Geology, 1979, 2(8): 8-13. https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFD7984&filename=SWDG197902001&v=MzI3MjR1eFlTN0RoMVQzcVRyV00xRnJDVVI3cWZidWRvRnkvaFVMdk5OanJQYWJLeEdkak1yWTlGWllSOGVYMUw=. (in Chinese)
[7] GB 50218–94. Standard for engineering classification of rock masses [S]. Beijing: China Planning Press, 1994: 1-78. (in Chinese).
[8] GB 50218–2014. Standard for engineering classification of rock masses [S]. Beijing: China Planning Press, 2014: 1-84. (in Chinese)
[9] BARTON N, QUADROS E. Anisotropy is everywhere, to see, to measure, and to model [J]. Rock Mechanics and Rock Engineering, 2015, 48(4): 1323-1339. DOI: 10.1007/ s00603-014-0632-7.
[10] BHASIN R, BARTON N, GRIMSTAD E, CHRYSSANTHSKIS P. Engineering geological characterization of low strength anisotropic rocks in the Himalayan region for assessment of tunnel support [J]. Engineering Geology, 1995, 40(3, 4): 169-193. DOI: 10.1016/0013-7952(95)00055-0.
[11] HOEK E, MAEINOS P, BENISSI M. Applicability of the geological strength index (GSI) classification for very weak and sheared rock masses. The case of the Athens Schist Formation [J]. Bulletin of Engineering Geology and the Environment, 1998, 57(2): 151-160. DOI: 10.1007/ s100640050031.
[12] SAROGLOU C, QI Sheng-wen, GUO Song-feng, WU Fa-quan. ARMR, a new classification system for the rating of anisotropic rock masses [J]. Bulletin of Engineering Geology and the Environment, 2019, 78(5): 3611-3626. DOI: 10.1007/s10064-018-1369-4.
[13] HUDSON J A, HARRISON J P. Engineering rock mechanics: An introduction to the principles [M]. Amsterdam: Elsevier. DOI: 10.1016/B978-008043010-2/50000-9.
[14] ISRM. Rock characterization, testing and monitoring: ISRM suggested methods [S]. Oxford: Pergamon Press, 1981.
[15] TSIDZI K. Propagation characteristics of ultrasonic waves in foliated rocks [J]. Bulletin of the International Association of Engineering Geology, 1997, 56: 103-113. https://www. researchgate.net/publication/292824606_Propagation_characteristics_of_ultrasonic_waves_in_foliated_rocks.
[16] TSIDZI K. The influence of foliation on point load strength anisotropy of foliated rocks [J]. Engineering Geology, 1990, 29(1): 49-58. DOI: 10.1016/0013-7952(90)90081-B.
[17] RAMAMURTHY T. Strength and modulus responses of anisotropic rocks [J]. Comprehensive Rock Engineering, 1993, 1: 313-329. https://www.researchgate.net/publication/ 279907562_Strength_and_modulus_responses_of_anisotropic_rocks.
[18] KWASNIEWSKI A M. Mechanical behavior of anisotropic rocks [J]. Comprehensive Rock Engineering, 1993, 1: 285-312. https://www.researchgate.net/publication/2795499 51_Mechanical_behavior_of_anisotropic_rocks.
[19] SAROGLOU H, TSIAMBAOS G. Classification of anisotropic rocks [C]// 11th Congress of the International Society for Rock Mechanics, 2007. DOI: 10.1017/S 0940739 1950003 85.
[20] ALIABADIAN Z, ZHAO Gao-feng, RUSSELL A. Failure, crack initiation and the tensile strength of transversely isotropic rock using the Brazilian test [J]. International Journal of Rock Mechanics & Mining Sciences, 2019, 122, 104073. DOI: 10.1016/ j.ijrmms.2019.10 4 073.
[21] SAROGLOU H. Engineering behaviour of anisotropic and heterogeneous layered rocks [C]// In Proceedings of the IAEG conference “Global view of engineering geology and the environment”. Beijing, China, 2013: 721-731. DOI: 10.1201/b15 794-116.
[22] BAGHERIPOUR M H, RAHGOZAR R, PASHNESAZ H, MALEKINEJAD M. A complement to Hoek-Brown failure criterion for strength prediction in anisotropic rock [J]. Geo-mechanics and Engineering, 2011, 3(1): 61-81. DOI: 10.12989/gae.20 11.3.1.061.
[23] MATSUKURA Y, HASHIZUME K, OGUCHI C T. Effect of microstructure and weathering on the strength anisotropy of porous rhyolite [J]. Engineering Geology, 2002, 63(1): 39-47. DOI: 10.1016/S0013-7952(01)00067-9.
[24] JAEGER J C. Shear failure of anisotropic rock [J]. Geological Magazine, 1960, 97(1): 65-72. DOI: 10.1017/ S00167568 00061100.
[25] TIEN Y M, KUO M C. A failure criterion for transversely isotropic rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 38(3): 399-412. DOI: 10.1016/ S1365-1609(01)00007-7.
[26] HOEK E. Fracture of anisotropic rock [J]. Journal of the South African Institute of Mining and Metallurgy, 1964, 64(10): 501-523. https://journals.co.za/content/saimm/64/10/ AJA0038223X_ 3802.
[27] WALSH J B, BRACE W F. A fracture criterion for brittle anisotropic rock [J]. Journal of Geophysical Research, 1964, 69(16): 3449-3456. DOI: 10.1029/ JZ069i016p03449.
[28] COLAK K, UNLU T. Effect of transverse anisotropy on the Hoek-Brown strength parameter 'mi' for intact rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 6(41): 1045-1052. DOI: 10.1016/ j.ijrmms.2004.04.004.
[29] SAROGLOU H, TSIAMBAOS G. A modified Hoek–Brown failure criterion for anisotropic intact rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(2): 223-234. DOI: 10.10 16/j.ijr mms.200 7.05.004.
[30] RAO K S, RAO G V, RAMAMURTHY T. A strength criterion for anisotropic rocks [J]. Ind Geotech J, 1986, 16(4): 317-333. https:// www. researchgate.net/publication/27971 7428_A_strength_criterion_for_anisotropic_rocks.
[31] RAMAMURTHY T, RAO G, SINGH J. A strength criterion for anisotropic rocks [C]// Proceedings of the fifth Australia–New Zealand Conference on Geomechanics. Australia: Institution of Engineers, 1988: 253. https://www. researchgate.net/publication/285492367_A_strength_criterion_for_anisotropic_rocks_In_Proceedings_of_the_fifth_Australia-New_Zealand_conference_on_geomechanics.
[32] NASSERI M H B, RAO K S, RAMAMURTHY T. Anisotropic strength and deformational behavior of Himalayan schists [J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(1): 3-23. DOI: 10.1016/S1365-1609(02)00103-X.
[33] SAEIDI O, VANEGHI R G, RASOULI V, GHOLAMI R. A modified empirical criterion for strength of transversely anisotropic rocks with metamorphic origin [J]. Bulletin of Engineering Geology and the Environment, 2013, 72(2): 257-269. DOI: 10.1007/s10064-013-0472-9.
[34] BIENIAWSKI Z T. The point-load test in geotechnical practice [J]. Engineering Geology, 1975, 9(1): 1-11. DOI: 10.1016/0013-7952(75) 90024 -1.
[35] FRANKLIN J A. Suggested method for determining point load strength [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1985, 22 (2): 51-60. DOI: 10.1016/0148-9062(85)92327-7.
[36] SINGH T N, KAINTHOLA A, VENKATESH A. Correlation between point load index and uniaxial compressive strength for different rock types [J]. Rock Mechanics and Rock Engineering, 2012, 45(2): 259-264. DOI: 10.1007/s00603- 011-0192-z.
[37] VASARHELYI B. Some observations regarding the strength and deformability of sandstones in dry and saturated conditions [J]. Bulletin of Engineering Geology and the Environment, 2003, 62(3): 245-249. DOI: 10.1007/s10064- 002-0186-x.
[38] DEERE D U. Technical description of rock cores for engineering purposes [J]. Rock Mechanics and Engineering Geology, 1964, 1(1): 16-22. https://www.researchgate.net/ publication/239665805_Technical_Description_of_Rock_Cores_for_Engineering_Purposes.
[39] RAMAMURTHY T, ARORA V K. Strength predictions for jointed rocks in confined and unconfined states [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1994, 31(1): 9-22. DOI: 10.1016/0148-9062(94)90973-3.
[40] VUTUKURI V S, HOSSAINI S M F, FOROUGHI M H. A study of the effect of roughness and inclination of weakness planes on the strength properties of rock and coal [C]// Proceedings of the 2nd International Conference on the Mechanics of Jointed and Faulted rock. Vienna, Austria, 1995: 151-155.
[41] GUO Song-feng, QI Sheng-wen, HUANG Xiao-lin. Anisotropy of rockmass strength and its transformation critical confining stress [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3222-3227. http://en.cnki.com.cn/Article_en/CJFDTOTAL-YSLX2013S2031.htm. (in Chinese)
[42] GUO Song-feng, QI Sheng-wen, ZHAN Zhi-fa, MA Li-na, GURE E G, ZHANG Shi-shu. Numerical study on the progressive failure of heterogeneous geomaterials under varied confining stresses [J]. Engineering Geology, 2020: 269. DOI: 10.1016/j.en ggeo.2020.105556.
[43] GUO Song-feng, QI Sheng-wen. Numerical study on progressive failure of hard rock samples with an unfilled undulate joint [J]. Engineering Geology, 2015, 193: 173-182. DOI: 10.1016/j.enggeo. 2015.04. 023.
[44] ZHOU Yu, WU Shun-chuan, GAO Yong-tao, MISRA A. Macro and meso analysis of jointed rock mass triaxial compression test by using equivalent rock mass (ERM) technique [J]. Journal of Central South University, 2014, 21(3): 1125-1135. DOI: 10.1 007/s11771-014-2045 -x.
[45] SAROGLOU H. Geological parameters affecting the geotechnical properties of intact rock. The effect of anisotropy [D]. Athens: National Technical University of Athens, 2007: 480.
[46] SHA Peng, WU Fa-quan, LI Xiang, LIANG Ning, CHANG Jin-yuan. Squeezing deformation in layered surrounding rock and force characteristics of support system of a tunnel under high in-situ stress [J]. Rock and Soil Mechanics, 2015, 36(5): 1407-1414. DOI: 10.16285/j.rsm.2015.05.024. (in Chinese)
[47] CHEN Yi-feng, WEI Kai, LIU Wu, HU Shao-hua, HU Ran, ZHOU Chuang-bing. Experimental characterization and micromechanical modelling of anisotropic slates [J]. Rock Mechanics and Rock Engineering, 2016, 49(9): 3541-3557. DOI: 10.1007/ s00603-016-1009-x.
(Edited by HE Yun-bin)
中文导读
A-BQ,一种基于BQ的各向异性岩体质量分级系统
摘要:自然界中岩体的力学行为多数表现为各向异性,现有的岩体质量分级方法大多是基于各向同性假设,因此远远难以满足工程要求。本研究在中国岩体质量分级标准BQ的基础上,提出了一种各向异性岩体质量分级系统A-BQ。该系统可用来评估岩体的各向异性程度,同时还可以对各向异性岩体的质量进行评估分级。系统中考虑了岩石的固有各向异性和岩体结构的各向异性,分别采用岩石强度的各向异性和岩体完整性系数的各向异性表征。岩体的各向异性程度通过不同作用方向下岩体的最好与最差质量得分之比确定,并由围岩应力进行调整。基于岩体各向异性结构的产状,结合岩体最好和最差质量得分,可计算各向异性岩体的基本得分,再通过应力状态和地下水因子的校正,获得各向异性岩体的ABQ值,在此基础上将岩体质量分为5级。针对不同岩体质量级别给出了隧道和边坡工程可能的稳定性状态和破坏模式。最后以实际的各向异性岩体隧道和边坡工程为例,对该分级方法进行了应用。
关键词:各向异性;岩体;基本质量;分级;隧道;边坡
Foundation item: Projects(41702345, 41825018) supported by the National Natural Science Foundation of China; Project(2019QZKK0904) supported by the Second Tibetan Plateau Scientific Expedition and Research Program (STEP), China; Project(KFZD-SW-422) supported by the Key Deployment Program of the Chinese Academy of Sciences
Received date: 2020-06-11; Accepted date: 2020-09-13
Corresponding author: QI Sheng-wen, PhD, Research Professor; Tel: +86-10-82998055; E-mail: qishengwen@mail.iggcas.ac.cn; ORCID: https://orcid.org/0000-0002-0967-758
Abstract: The rock mass in nature is in most cases anisotropic, while the existing classifications are mostly developed with the assumption of isotropic conditions that not always meet the engineering requirements. In this study, an anisotropic system based on China National Standard of BQ, named as A-BQ, is developed to address the classification of anisotropic rock mass incorporating the anisotropy degree as well as the quality of rock mass. Two series of basic rating factors are incorporated including inherent anisotropy and structure anisotropy. The anisotropy degree of rock mass is characterized by the ratio of maximum to minimum quality score and adjusted by the confining stress. The quality score of rock mass is determined by the key factors of anisotropic structure occurrence and the correction factors of stress state and groundwater condition. The quality of rock mass is characterized by a quality score and classified in five grades. The assessment of stability status and probable failure modes are also suggested for tunnel and slope engineering for different quality grades. Finally, two cases of tunnel and slope are presented to illustrate the application of the developed classification system into the rock masses under varied stress state.


